Стоит использовать формулы, которые есть для данной фигуры.
Согласно правилам, для определения площади параллелепипеда надо знать его стороны.
S = 2(ab + ac + bc).
Однако, в самом примере мы знаем только два стороны из трех. Но нам известен и объем фигуры, который вычисляется формуле.
V = abc.
V = 112 см3, a=2, b=7.
с = V/ab = 112/2*7 = 112/14 = 8.
Теперь можно высчитать площадь:
S = 2(2*7 + 2*8 + 7*8) = 2(14 + 16 + 56) = 2 * 86 = 172 см2.
При желании можно было бы написать написать одну формулу, соединив все, без отдельного вычисления третьей стороны. Но так она была бы слишком большой и легко можно было бы допустить ошибку.
In geometry, students must often calculate surface areas and volumes of different geometric shapes such as spheres, cylinders, rectangular prisms or cones. For these types of problems, it is important to know the formulas for both surface area and volume of these figures. It also helps to understand what the definitions of surface area and volume are. Surface area is the total area of all exposed surfaces of a given three-dimensional figure or object. Volume is the amount of space occupied by this figure. You can easily calculate surface area from volume by applying the right formulas.
-
A T1-83 Plus calculator was used to find the cubic root in Step 6. Using this calculator to find a solution, you must press the “MATH” function key first and then find the function key for cubic roots. Since there may be differences in the use of other calculator models, check the user manuals for instructions on calculating cubic roots.
Solve surface area problem of any geometric figure when given its volume by knowing the formulas. For instance, the formula for surface area of a sphere is given by SA= 4?(r^2), while its volume (V) is equal to (4/3)?(r^3) where «r» is the radius of the sphere. Note that most formulas for surface area and volume for various figures are available online (see the Resources).
Use the formulas in Step 1 to calculate the surface area for a sphere with a volume of 4.5? cubic feet where ? (pi) is approximately 3.14.
Find the radius of the sphere by substituting 4.5? ft^3 for V in the formula in Step 1 to get: V=4.5? cubic feet.= (4/3)?(r^3)
Multiply each side of the equation by 3 and the equation becomes: 13.5 ? cubic feet =4?(r^3)
Divide both sides of the equation by 4? in Step 4 to solve for the radius of the sphere. To get: (13.5? cubic feet)/(4?) =(4? )(r^3)/ (4?), which then becomes: 3.38 cubic feet= (r^3)
Use the calculator to find the cubic root of 3.38 and subsequently the value of the radius “r” in feet. Find the function key designated for cubic roots, press this key and then enter the value 3.38. You find that the radius is 1.50 ft. You can also use an online calculator for this calculation (see the Resources).
Substitute 1.50 ft. in the formula for SA= 4?(r^2) found in Step 1. To find: SA = 4?(1.50^2) = 4?(1.50X1.50) is equal to 9? square ft.
Substituting the value for pi= ?= 3.14 in the answer 9? square ft., you find that the surface area is 28.26 square ft. To solve these types of problems, you need to know the formulas for both surface area and volume.
Tips
В геометрии студенты должны часто вычислять площади поверхности и объемы различных геометрических форм, таких как сферы, цилиндры, прямоугольные призмы или конусы. Для задач такого типа важно знать формулы как для площади поверхности, так и для объема этих фигур. Это также помогает понять, каковы определения площади поверхности и объема. Площадь поверхности — это общая площадь всех открытых поверхностей данной трехмерной фигуры или объекта. Объем — это объем пространства, занимаемого этой фигурой. Вы можете легко рассчитать площадь поверхности от объема, применяя правильные формулы.
-
Калькулятор T1-83 Plus использовался для поиска кубического корня на шаге 6. Используя этот калькулятор, чтобы найти решение, вы должны сначала нажать функциональную клавишу «MATH», а затем найти функциональную клавишу для кубических корней. Поскольку могут быть различия в использовании других моделей калькулятора, обратитесь к руководствам пользователя для получения инструкций по вычислению кубических корней.
Решите проблему площади поверхности любой геометрической фигуры, учитывая ее объем, зная формулы. Например, формула для площади поверхности сферы определяется как SA = 4? (R ^ 2), а ее объем (V) равен (4/3)? (R ^ 3), где «r » это радиус сферы. Обратите внимание, что большинство формул для площади поверхности и объема для различных фигур доступны онлайн (см. Ресурсы).
Используйте формулы в шаге 1 для расчета площади поверхности для сферы с объемом 4, 5? кубических футов где? (пи) составляет примерно 3, 14.
Найти радиус сферы, подставив 4.5? ft ^ 3 для V в формуле на шаге 1, чтобы получить: V = 4, 5? кубические футы. = (4/3)? (r ^ 3)
Умножьте каждую часть уравнения на 3, и уравнение получится: 13, 5? кубических футов = 4? (г ^ 3)
Разделите обе части уравнения на 4? на шаге 4, чтобы решить для радиуса сферы. Чтобы получить: (13, 5? Кубических футов) / (4?) = (4?) (R ^ 3) / (4?), Который затем становится: 3, 38 кубических футов = (r ^ 3)
Используйте калькулятор, чтобы найти кубический корень 3, 38, а затем значение радиуса «r» в футах. Найдите функциональную клавишу, предназначенную для кубических корней, нажмите эту клавишу и введите значение 3, 38. Вы обнаружите, что радиус составляет 1, 50 фута. Вы также можете использовать онлайн калькулятор для этого расчета (см. Ресурсы).
Замените 1, 50 фута в формуле для SA = 4? (R ^ 2), найденного на шаге 1. Найти: SA = 4? (1.50 ^ 2) = 4? (1.50X1.50) равно 9? квадратный фут
Подставляя значение для пи =? = 3, 14 в ответе 9? квадратных футов, вы обнаружите, что площадь поверхности составляет 28, 26 квадратных футов. Чтобы решить эти типы проблем, вам нужно знать формулы как для площади поверхности, так и для объема.
подсказки
Площадь поверхности куба, формулы и примеры / Блог :: Бингоскул
- Блог
- →
- Площадь поверхности куба, формулы и примеры
Формулы для нахождения площади поверхности куба:
Существует две формулы:
- Через длину грани H: S=6*H^2
- Через длину диагонали d: S=6*H^2=6*(frac{d}{sqrt{3}})
Как найти площадь поверхности куба?
- Чтобы найти с гранью H, надо сложить сумму площадей всех его граней, то есть вычислить площадь квадрата со стороной H, и умножить полученный результат на 6.
S=6*H - Если известна только диагональ грани куба, надо его диагональ d поделить на квадратный корень из трёх и результат умножить на 6.
S=6*(frac{d}{sqrt{3}})
Примеры
- Дан куб с ребром H = 7. Для начала возведем длину его грани в квадрат:
H2 = H * H = 7 * 7 = 49. Мы получили периметр одной грани.
Для вычисления площади результат из первого действия умножим на количество граней:
S = 6 * 49 = 249.
Мы получили искомый результат.
Ответ: 294. - Дан куб с диагональю ребра d=13. Требуется найти площадь его поверхности
Вычислим его грань H, исходя из формулы H=frac{d}{sqrt{3}}= frac{13}{sqrt{3}}= 7,51.
Теперь, когда нам известна величина грани куба, воспользуемся первой формулой, и умножим результат на 6 :
S = 6 * H2 = 6 * 7,5122 = 6 * 56,43 ≈ 338.
Мы снова получили искомый результат.
Ответ: 338.
Площадь поверхности прямоугольного параллелепипеда равна
Sпов = (аb + bc + ac) * 2
Так как у куба а = b = c
Sпов. куба = (аа + аа +аа) * 2 = 6 а2
Sпов. куба = 6 а2
Пример. Площадь поверхности куба равна 18. Найдите его диагональ.
Пусть ребро куба равно а.
Sпов. куба = 6 а2
6а^2 =18
a=sqrt{3}
Delta BB_{1}D:B_{1}D=sqrt{BB_1^2+BD^2}
B_1D=a*sqrt{3}
B_1D=3
bingoschool.ru
Площадь боковой поверхности куба | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Площадь боковой поверхности куба объединяет в себе все боковые грани куба, которые представляют собой квадраты с равными сторонами и площадями. Поэтому площадь боковой поверхности куба равна ребру, возведенному во вторую степень и умноженному на четыре, а ребро куба, выраженное через площадь боковой поверхности, равно квадратному корню из площади, деленному на 2.
S_(б.п.)=4a^2
a=√(S_(б.п.)/4)=√(S_(б.п.) )/2
Вычислить площадь одной грани куба через площадь боковой поверхности можно не прибегая к извлечению квадратного корня, исходя из ее определения. Для этого нужно площадь боковой поверхности разделить на количество граней – 4. Чтобы найти площадь полной поверхности через площадь боковой поверхности, необходимо разделить последнюю на 4 и умножить на 6.
S=S_(б.п.)/4
S_(п.п.)=6/4 S_(б.п.)=(3S_(б.п.))/2
Объем куба обычно рассчитывается как третья степень ребра куба, для того чтобы вычислить объем куба через площадь боковой поверхности нужно подставить вместо ребра выведенную раннее формулу.
V=a^3=(√(S_(б.п.) )/2)^3=√(〖S_(б.п.)〗^3 )/8
Периметр куба является длиной всех его ребер a, следовательно, для его нахождения необходимо умножить одно ребро на 12. Чтобы найти периметр куба через площадь боковой поверхности, подставим вместо стороны a половину квадратного корня из площади.
P=12a=12 √(S_(б.п.) )/2=6√(S_(б.п.) )
Чтобы вычислить диагональ стороны куба, наиболее быстрым способом будет воспользоваться формулой для диагонали квадрата, которая равна стороне квадрата, умноженной на корень из двух. Так как ребро куба, являющееся по совместительству стороной квадрата, равно корню из площади боковой поверхности, деленному на два, то диагональ стороны куба будет равна квадратному корню из площади, деленной на два, полученному в ходе преобразования коэффициентов.
d=a√2=√(S_(б.п.) )/2 √2=√(S_(б.п.)/2)
Найти диагональ куба можно из прямоугольного треугольника, который можно получить, соединив боковое ребро и диагональ куба через диагональ основания. По теореме Пифагора, диагональ куба будет равна ребру куба, умноженному на корень из трех. (рис.2.1)
a^2+d^2=D^2
D^2=a^2+2a^2
D^2=3a^2
D=a√3=√(3S_(б.п.) )/2
Если в куб вписать сферу, то ее радиус становится равным половине ребра куба, или квадратному корню из площади боковой поверхности, разделенной на 4. (рис. 2.2)
r=a/2=√(S_(б.п.) )/4
Радиус сферы, описанной вокруг куба, можно найти через площадь боковой поверхности, если, умножив ее на три, извлечь квадратный корень и разделить его на 4. (рис.2.3)
R=D/2=√(3S_(б.п.) )/2
geleot.ru
Как найти площадь поверхности куба?
Куб представляет собой объемный вариант квадрата. Зная длину ребра куба (а), можно воспользоваться наиболее распространенной формулой по определению площади поверхности (S). Исходя из того, что площадь квадрата соответствует длине возведенной в квадрат грани, и у куба их шесть, получается: S = 6∙a². Эта формула определяет площадь полной поверхности куба.
Способы определения площади куба
- Если задан объем (V) пространства, что ограничен сторонами куба, а длина ребра неизвестна, то площадь (S) определяется таким образом.
Когда единственно известная величина фигуры, представляет собой возведенную в третью степень длину ребра, тогда размер длины стороны каждой грани куба определяют посредством извлечения кубического корня из имеющегося параметра. Формула площади поверхности куба имеет вид: S = 6∙(³√V)².
- Когда задана длина диагонали гексаэдра (L), тогда длину одной грани можно легко вычислить, а вместе с ней и площадь фигуры. Диагональ определяют так: L/v3. А площадь куба поэтому вычисляется так: S = 6∙(L/√3)² = 2∙L², что очень удобно при расчетах.
- Как найти площадь поверхности куба, когда указан радиус описанной около гексаэдра сферы (R)? Просто! Необходимо только применить формулу такую: S = 8∙R²= 2∙(2∙R)². Такое возможно благодаря тому, что диагональ куба соответствует параметру диаметра сферы.
- Зная радиус вписанной в гексаэдр окружности, формулу площади поверхности куба записывают так: S = 24∙r².
Площадь боковой поверхности куба
S = s1+s2+s3+s4, в которой слагаемые представляют собой площади четырех параллелограммов соответственно, которые образуют боковую поверхность параллелепипеда.
Формула площади боковой поверхности куба может быть представлена как S = P•h при условии, что задан прямой параллелепипед, с известным периметром основания P и высотой h.
Когда расчеты нужно провести по прямоугольному п
elhow.ru
Как найти площадь поверхности куба если объем известен
То есть если известны длины двух сторон треугольника , которые равны и , а также угол между этими сторонами, то искомая площадь: Формула площади треугольника. Второй способ. Чтобы найти площадь треугольника, нужно сторону умножить на высоту, проведенную к этой стороне (рис.
Как найти площадь поверхности куба, если его объём равен 125 см в кубе?
Ответы и объяснения
- m11m главный мозг
A=5 (см) — ребро куба
S=6*5²=6*25=150 (см²) — площадь поверхности куба
Как найти площадь поверхности куба если объем известен
Как найти площадь поверхности куба, если его объём равен 125 см в кубе?
Ответы и объяснения
- m11m главный мозг
A=5 (см) — ребро куба
S=6*5²=6*25=150 (см²) — площадь поверхности куба
Как найти площадь поверхности куба если объем известен
Как найти площадь поверхности куба?
Куб представляет собой объемный вариант квадрата. Зная длину ребра куба (а), можно воспользоваться наиболее распространенной формулой по определению площади поверхности (S). Исходя из того, что площадь квадрата соответствует длине возведенной в квадрат грани, и у куба их шесть, получается: S = 6∙a². Эта формула определяет площадь полной поверхности куба.
Способы определения площади куба
Если задан объем (V) пространства, что ограничен сторонами куба, а длина ребра неизвестна, то площадь (S) определяется таким образом.
Когда единственно известная величина фигуры, представляет собой возведенную в третью степень длину ребра, тогда размер длины стороны каждой грани куба определяют посредством извлечения кубического корня из имеющегося параметра. Формула площади поверхности куба имеет вид: S = 6∙(³√V)².
Площадь боковой поверхности куба
S = s1+s2+s3+s4, в которой слагаемые представляют собой площади четырех параллелограммов соответственно, которые образуют боковую поверхность параллелепипеда.
Формула площади боковой поверхности куба может быть представлена как S = P•h при условии, что задан прямой параллелепипед, с известным периметром основания P и высотой h.
Когда расчеты нужно провести по прямоугольному параллелепипеду (все его грани — прямоугольники), с известными длинами сторон основания (d и c), когда как k — боковое ребро фигуры, тогда площадь боковой поверхности куба определяют как: S = 2•k•(d+c).
poiskvstavropole.ru
Площадь куба | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Площадь куба, она же площадь полной поверхности куба, равна увеличенной в шесть раз площади одной его грани. Так как площадь куба зависит только от ребра, зная ее, можно легко вычислить ребро и затем все остальные параметры куба.
S_(п.п.)=6a^2
a=√(S_(п.п.)/6)
Соответственно, площадь стороны куба – одной его грани, будет равна площади полной поверхности разделенной на шесть, а площадь боковой поверхности, состоящей из четырех граней, — двум третям площади полной поверхности куба.
S=S_(п.п.)/6
S_(б.п.)=2/3 S_(п.п.)
Для того чтобы найти объем куба, необходимо его ребро возвести в третью степень. Используя полученную формулу ребра куба через площадь полной поверхности, получим, что объем куба равен одной шестой квадратного корня из площади куба в третьей степени, деленной на шесть.
V=a^3=(√(S_(п.п.)/6))^3=1/6 √(〖S_(п.п.)〗^3/6)
Периметр куба можно найти, умножив ребро куба на 12. Если подставить вместо ребра квадратный корень через площадь куба, то получим следующую формулу для периметра куба:
P=12a=12√(S_(п.п.)/6)
Диагональ одной стороны куба является по определению диагональю квадрата, которая вычисляется как произведение стороны квадрата на корень из двух. Так как ребро куба является стороной этого квадрата, то диагональ будет равна квадратному корню из площади, деленной на 3.
d=a√2=√(S_(п.п.)/3)
Чтобы рассчитать диагональ куба, необходимо провести дополнительное построение на чертеже, соединяющее ребро куба и одну из вершин диагонали в прямоугольный треугольник. Это дает возможность воспользоваться теоремой Пифагора и вычислить диагональ куба через площадь, подставив формулу вместо ребра куба. (рис.2.1)
a^2+d^2=D^2
D^2=a^2+2a^2
D^2=3a^2
D=a√3=√(S_(п.п.)/2)
Радиус сферы, вписанной в куб, по определению равен половине ребра куба или половине квадратного корня из площади куба, деленной на шесть. (рис. 2.2)
r=a/2=1/2 √(S_(п.п.)/6)
Радиус сферы, описанной вокруг куба, представлен половиной диагонали куба, которая равна площади полной поверхности куба, деленной на два, под корнем. (рис.2.3)
R=D/2=1/2 √(S_(п.п.)/6)
geleot.ru
Как найти объем куба. Формулы нахождения объема куба. Из этой статьи вы узнаете как найти площадь куба разными способами
Существует 3 основных способа нахождения площади куба. Каждый применяется в зависимости от условия задачи. Рассмотрим каждый из них.
1
Как найти объем куба – способ 1
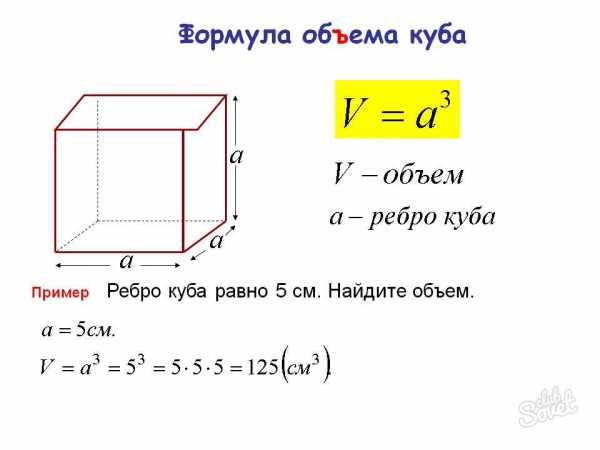
Самый простой способ нахождения объема куба – возведение в куб одного из его ребер. Так как у куба все 12 ребер равны, то формула выглядит так V=a3 или V=а*а*а. Если в условии дано ребро, вставьте его значение в формулу и получите правильный ответ. Если длина ребра не дана – придется сначала ее найти. Пример: ребро куба равно 5 см. Найти объем. V = a3 = 53 = 125
2
Как найти объем куба – способ 2
Найти объем куба можно при помощи формулы площади поверхности куба: S=6a3. Скажем, площадь поверхности куба = 54 см2. Тогда a2 = 54/6 = 9. а, соответственно = 3. V = 33 = 27 см3.
3
Как найти объем куба – способ 3
В случае, если нам известна диагональ одной из грани (важно помнить, что диагональ не куба, а именно грани), то поделив его на √2, вы получите длину ребра куба, то есть а. После этого, по старой доброй формуле возводим а в куб и получаем правильный ответ.
sovetclub.ru
Как найти площадь поверхности куба?
Куб обладает множеством интересных математических свойств и известен людям с давних времен. Представители некоторых древнегреческих школ считали, что элементарные частицы (атомы), из которых состоит наш мир, имеют форму куба, а мистики и эзотерики даже обожествляли эту фигуру. И сегодня представители паранауки приписывают кубу удивительные энергетические свойства.
Куб — это идеальная фигура, одно из пяти Платоновых тел. Платоново тело — это

1. Все ее ребра и грани равны.
2. Углы между гранями равны (у куба углы между гранями равны и составляют 90 градусов).
3. Все вершины фигуры касаются поверхности описанной вокруг нее сферы.
Точное количество этих фигур назвал древнегреческий математик Теэтет Афинский, а ученик Платона Евклид в 13-ой книге Начал дал им подробное математическое описание.
Древние греки, склонные с помощью количественных величин описывать строение нашего мира, придавали Платоновым телам глубокий сакральный смысл. Они считали, что каждая из фигур символизирует вселенские начала: тетраэдр — огонь, куб — землю, октаэдр — воздух, икосаэдр — воду, додекаэдр — эфир. Сфера же, описанная вокруг них, символизировала совершенство, божественное начало.
Итак, куб, называемый также гексаэдром (от греч. «hex» — 6), — это трехмерная правильная геометрическая фигура. Его также называют правильной четырехугольной призмой или прямоугольным параллелепипедом.
У куба шесть граней, двенадцать ребер и восемь вершин. В эту фигуру можно вписать другие правильные многогранники: тетраэдр (четырехгранник с гранями в виде треугольников), октаэдр (восьмигранник) и икосаэдр (двадцатигранник).
Диагональю куба называется отрезок, соединяющий две симметричные относительно центра вершины. Зная длину ребра куба a, можно найти длину диагонали v: v = a3.
В куб, как говорилось выше, можно вписать сферу, при этом радиус вписанной сферы (обозначим r) будет равен половине длины ребра: r =(1/2)а.
Если же сферу описать вокруг куба, то радиус описанной сферы (обозначим его R) будет равен: R= ( 3/2)a.
Довольно распространенный в школьных задачах вопрос: как вычислить площадь
Аналогично тому, как мы нашли площадь поверхности куба, рассчитаем площадь его боковых граней: Sб=4а2.
Из этой формулы понятно, что две противолежащие грани куба — это основания, а остальные четыре — боковые поверхности.
Отыскать площадь поверхности куба можно и другим способом. Учитывая тот факт, что куб — это прямоугольный параллелепипед, можно воспользоваться понятием трех пространственных измерений. Это значит, что куб, являясь трехмерной фигурой, имеет 3 параметра: длину (а), ширину(b) и высоту (c).
Используя эти параметры, вычислим площадь полной поверхности куба: Sп= 2(ab+ас+bc).
Чтобы рассчитать площадь боковой поверхности куба, периметр основания необходимо умножить на высоту: S
б= 2c(a+b).
Объем куба — это произведение трех составляющих — высоты, длины и ширины:
V= abc либо трех смежных ребер: V=а3.
fb.ru
Формулировка задачи: Объем куба равен V. Найдите площадь его поверхности.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13 (Задачи по стереометрии).
Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.
Пример задачи:
Объем куба равен 8. Найдите площадь его поверхности.
Решение:
Сторону куба можно получить из его объема:
Теперь можно вычислить площадь поверхности куба по его стороне:
S = 6 ⋅ a2 = 6 ⋅ 22 = 24
Ответ: 24
В общем виде решение данной задачи по стереометрии выглядит следующим образом:
a = ∛V – сторона куба
S = 6a2 = 6 ⋅ (∛V)2
где V – объем куба.
Остается лишь подставить конкретные значения и подсчитать результат.
Поделитесь статьей с одноклассниками «Дан объем куба, найдите площадь его поверхности – как решать».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.