В данной публикации мы рассмотрим, как можно найти площадь поверхности куба и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади куба
- 1. Через длину ребра
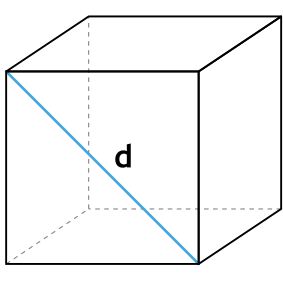
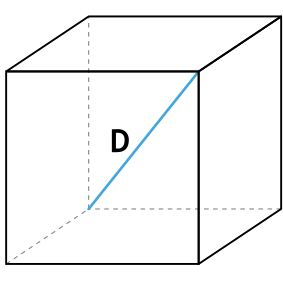
- 2. Через длину диагонали грани
- Примеры задач
Формула вычисления площади куба
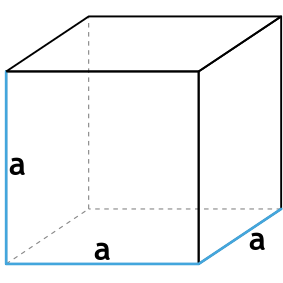
1. Через длину ребра
Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате.
S = 6 ⋅ a2
Данная формула получена следующим образом:
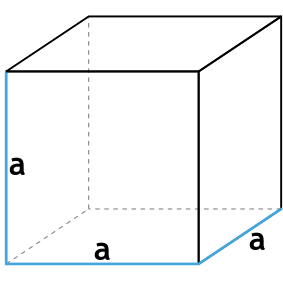
- Куб – это правильная геометрическая фигура, все грани которого являются равными квадратами с длиной стороны a (одновременно является ребром куба).
- Площадь каждой грани считается так: S = a ⋅ a = a2.
- Всего у куба 6 граней, а значит, площадь его поверхности равняется шести площадям одной грани: S = 6 ⋅ a2.
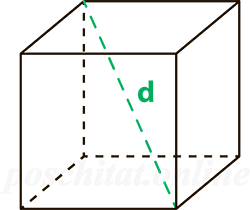
2. Через длину диагонали грани
Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√2.
Это значит, что вычислить площадь поверхности фигуры можно так:
S = 6 ⋅ (d/√2)2
Примеры задач
Задание 1
Найдите площадь поверхности куба, если длина его ребра составляет 12 см.
Решение:
Используем первую формулу выше и получаем:
S = 6 ⋅ (12 см)2 = 864 см2.
Задание 2
Площадь поверхности куба равняется 294 см2. Вычислите длину его ребра.
Решение:
Примем ребро куба за a. Из формулы расчета площади следует:
Задание 3
Вычислите площадь поверхности куба, если диагональ его грани равняется 5 см.
Решение:
Воспользуемся формулой, в которой задействована длина диагонали:
S = 6 ⋅ (5 см : √2)2 = 75 см2.
Площадь поверхности куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности куба
Чтобы посчитать площадь поверхности куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чему равна площадь поверхности куба, если:
длина ребра a =
Sпов =
0
Округление ответа:
Чему равна площадь поверхности куба, если:
длина диагонали d =
Sпов =
0
Округление ответа:
Чему равна площадь поверхности куба, если:
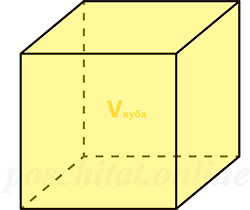
объём Vкуба =
Sпов =
0
Округление ответа:
Теория
Площадь поверхности куба через ребро
Чему равна площадь поверхности куба Sпов, если длина его ребра a:
Формула
Sпов = 6 ⋅ a²
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если он имеет длину рёбер a = 5 см :
Sпов = 6 ⋅ 5² = 6 ⋅ 25 = 150 см²
Площадь поверхности куба через диагональ
Чему равна площадь поверхности куба Sпов, если длина диагонали этого куба d:
Формула
Sпов = 2 ⋅ d²
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если длина диагонали у него d = 3 м:
Sпов = 2 ⋅ 3² = 2 ⋅ 9 = 18 м² = 180 000 см²
Площадь поверхности куба через объем
Чему равна площадь поверхности куба Sпов, если объём куба Vкуба:
Формула
Sпов = 6 ⋅ ³√Vкуба²
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если его объём Vкуба = 8 см³:
Sпов = 6 ⋅ 3√8² = 6 ⋅3√64 = 6 ⋅ 4 = 24 см²
См. также
Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.
Онлайн-калькулятор площади поверхности куба
У куба есть двенадцать ребер, то есть, отрезков, которые являются сторонами квадратов.
Также он имеет восемь вершин и шесть граней.
У куба есть диагональ, соединяющая противоположные вершины.
Формула площади поверхности куба
Площадь поверхности куба – это сумма площадей всех его граней:
S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6
Площадь каждой грани одинакова, то есть:
S1=S2=S3=S4=S5=S6=S′S_1=S_2=S_3=S_4=S_5=S_6=S’
S′S’ — площадь любой грани куба.
Тогда полная площадь поверхности куба запишется как:
S=6⋅S′S=6cdot S’
Рассмотрим на примерах разные способы вычисления полной площади поверхности куба.
Формула площади поверхности куба по длине ребра куба
Площадь каждой грани куба вычисляется как площадь квадрата, со стороной ребра куба по формуле:
S′=a⋅a=a2S’=acdot a=a^2
aa — сторона куба.
Отсюда, окончательно площадь поверхности куба:
S=6⋅a2S=6cdot a^2
aa — длина стороны куба.
Найти площадь поверхности куба, если длина его ребра равна 12 (см.).
Решение
a=12a=12
S=6⋅a2=6⋅122=6⋅144=864S=6cdot a^2=6cdot 12^2=6cdot 144=864 (см. кв.)
Ответ: 864 см. кв.
Формула площади поверхности куба по диагонали куба
По теореме Пифагора, диагональ куба связанна с длиной его ребра по формуле:
d2=a2+a2+a2d^2=a^2+a^2+a^2
d2=3⋅a2d^2=3cdot a^2
d=3⋅ad=sqrt{3}cdot a
Отсюда:
a=d3a=frac{d}{sqrt{3}}
Подставим в формулу для площади:
S=6⋅a2=6⋅(d3)2=2⋅d2S=6cdot a^2=6cdotBig(frac{d}{sqrt{3}}Big)^2=2cdot d^2
S=2⋅d2S=2cdot d^2
dd — диагональ куба.
Одна четвертая часть диагонали куба равна 2 (см.). Найти площадь поверхности куба.
Решение
14⋅d=2frac{1}{4}cdot d=2
Найдем диагональ:
d=4⋅2=8d=4cdot 2=8
Площадь:
S=2⋅d2=2⋅82=2⋅64=128S=2cdot d^2=2cdot 8^2=2cdot 64=128 (см. кв.)
Ответ: 128 см. кв.
Формула площади поверхности куба по длине диагонали квадрата (грани куба)
По теореме Пифагора, диагональ квадрата ll связанна с его стороной aa:
l2=a2+a2l^2=a^2+a^2
l2=2⋅a2l^2=2cdot a^2
l=2⋅al=sqrt{2}cdot a
Тогда сторона квадрата:
a=l2a=frac{l}{sqrt{2}}
Подставляем в формулу для площади и получаем:
S=6⋅a2=3⋅l2S=6cdot a^2=3cdot l^2
S=3⋅l2S=3cdot l^2
ll — диагональ квадрата (грани куба).
Одна четвертая часть диагонали квадрата равна 1 (см). Найти площадь поверхности куба, образованного данным четырехугольником.
Решение
14⋅l=1frac{1}{4}cdot l=1
Найдем диагональ квадрата:
l=4⋅1=4l=4cdot 1=4
Тогда площадь:
S=3⋅l2=3⋅42=48S=3cdot l^2=3cdot 4^2=48 (см. кв.)
Ответ: 48 см. кв.
Разберем более сложные примеры.
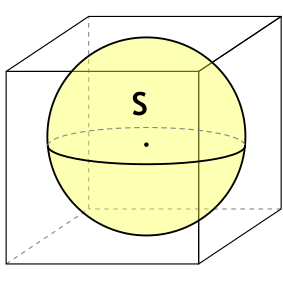
Формула площади поверхности куба по площади вписанного в куб шара
В куб вписан шар площади SшарS_{text{шар}}. Тогда радиус RR этого шара равен половине длины стороны куба aa:
R=a2R=frac{a}{2}
Площадь шара дается формулой:
Sшар=4⋅π⋅R2S_{text{шар}}=4cdotpicdot R^2
Отсюда найдем радиус шара:
R=Sшар4⋅πR=sqrt{frac{S_{text{шар}}}{4cdotpi}}
Сторона грани куба:
a=2⋅R=2⋅Sшар4⋅πa=2cdot R=2cdotsqrt{frac{S_{text{шар}}}{4cdotpi}}
Наконец площадь поверхности куба:
S=6⋅a2=6⋅SшарπS=6cdot a^2=frac{6cdot S_{text{шар}}}{pi}
S=6⋅SшарπS=frac{6cdot S_{text{шар}}}{pi}
SшарS_{text{шар}} — площадь шара, вписанного в куб.
В куб вписан шар, площадь которого равна 64 “пи” (см. кв.). Найти полную площадь поверхности куба.
Решение
Sшар=64πS_{text{шар}}=64pi
По формуле:
S=6⋅Sшарπ=6⋅64⋅ππ=384S=frac{6cdot S_{text{шар}}}{pi}=frac{6cdot 64cdotpi}{pi}=384 (см. кв.)
Ответ: 384 см. кв.
Не знаете, кто сможет решить контрольную работу на заказ для вас? Наши эксперты с удовольствием окажут вам помощь!
Тест по теме “Площадь поверхности куба”

{S_{полн}=6a^2}
На этой странице мы собрали формулы, которые помогут найти площадь полной и боковой поверхности куба. А чтобы упростить расчет у нас есть калькулятор, который сделает это быстро и точно.
В дополнение на сайте можно найти объем куба.
Куб — фигура, представляющая собой правильный многогранник, все грани которого являются квадратами. Все ребра (стороны) куба равны между собой.
Содержание:
- калькулятор площади поверхности куба
- площадь полной поверхности куба
- формула площади полной поверхности куба через ребро
- формула площади полной поверхности куба через диагональ грани
- формула площади полной поверхности куба через диагональ куба
- формула площади полной поверхности куба через периметр грани
- формула площади полной поверхности куба через периметр куба
- формула площади полной поверхности куба через объем
- формула площади полной поверхности куба через площадь вписанного шара
- площадь боковой поверхности куба
- формула площади боковой поверхности куба через ребро
- формула площади боковой поверхности куба через диагональ грани
- формула площади боковой поверхности куба через диагональ куба
- формула площади боковой поверхности куба через периметр грани
- формула площади боковой поверхности куба через периметр куба
- формула площади боковой поверхности куба через объем
- примеры задач
Что такое площадь полной поверхности куба
Куб состоит из сторон, которые называют гранями. Каждая такая грань представляет собой квадрат, а всего у куба 6 граней. Площади всех этих граней равны между собой и сложив все площади всех шести граней куба мы получим площадь полной поверхности куба.
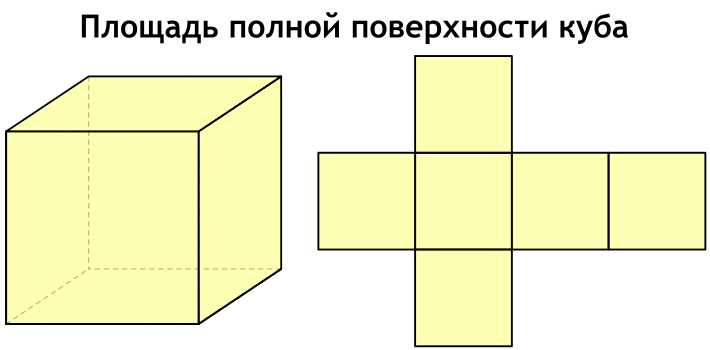
Площадь полной поверхности куба – это сумма площадей всех его граней.
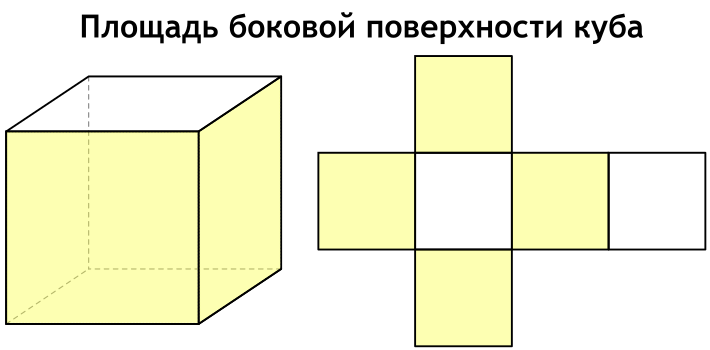
Площадь полной поверхности удобно представить, если посмотреть на развертку куба.
Формула площади полной поверхности куба через ребро
{S_{полн}=6a^2}
a — ребро куба
Формула площади полной поверхности куба через диагональ грани
{S_{полн}=3d , ^2}
d — диагональ грани куба
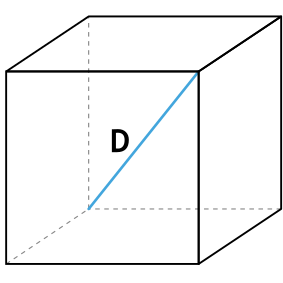
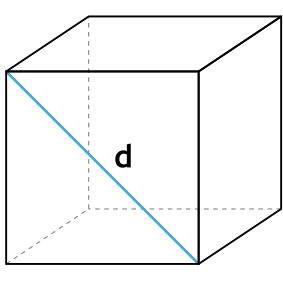
Формула площади полной поверхности куба через диагональ куба
{S_{полн}=2D^2}
D — диагональ куба
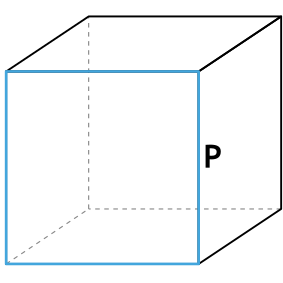
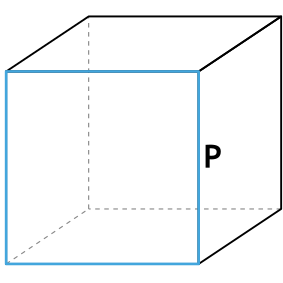
Формула площади полной поверхности куба через периметр грани
{S_{полн}= dfrac{3}{8}P^2}
P — периметр грани куба
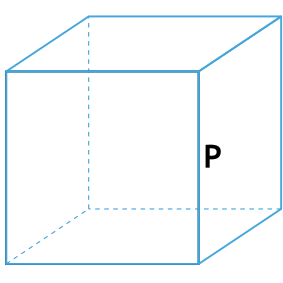
Формула площади полной поверхности куба через периметр куба
{S_{полн}= dfrac{P^2}{24}}
P — периметр куба
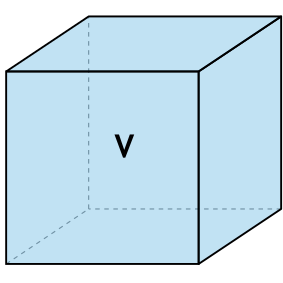
Формула площади полной поверхности куба через объем
{S_{полн}= 6{(sqrt[3]{V})}^2}
V — объем куба
Формула площади полной поверхности куба через площадь вписанного шара
{S_{полн}= 6 dfrac{S}{pi}}
S — площадь вписанного в куб шара
Что такое площадь боковой поверхности куба
Боковая поверхность куба — сумма площадей всех его боковых граней, которых у куба четыре.
Формула площади боковой поверхности куба через ребро
{S_{бок} = 4a^2}
a — ребро куба
Формула площади боковой поверхности куба через диагональ грани
{S_{бок}=2d , ^2}
d — диагональ грани куба
Формула площади боковой поверхности куба через диагональ куба
{S_{бок}=dfrac{4}{3}D^2}
D — диагональ куба
Формула площади боковой поверхности куба через периметр грани
{S_{бок}= dfrac{P^2}{4}}
P — периметр грани куба
Формула площади боковой поверхности куба через периметр куба
{S_{бок}= dfrac{P^2}{36}}
P — периметр куба
Формула площади боковой поверхности куба через объем
{S_{бок}= 4{(sqrt[3]{V})}^2}
V — объем куба
Примеры задач на нахождение площади поверхности куба
Задача 1
Найдите площадь поверхности куба, если его объем равен 125см³.
Решение
Для нахождения площади полной поверхности куба через его объем, нам поможет эта формула.
S_{полн} = 6{(sqrt[3]{V})}^2 = 6{(sqrt[3]{125})}^2 = 6{(5)}^2 = 6 cdot 25 = 150 : см²
Ответ: 150 см²
Проверить ответ нам поможет калькулятор .
Задача 1
Найдите площадь боковой поверхности куба с ребром 4см.
Решение
Для нахождения площади боковой поверхности куба с известной длиной ребра используем эту формулу.
S_{бок} = 4a^2 = 4 cdot 4^2 = 4 cdot 16 = 64 : см²
Ответ: 64 см²
Проверка .
Download Article
Download Article
The surface area of an object is the combined area of all of the sides on its surface. All six sides of a cube are congruent, so to find the surface area of a cube, all you have to do is find the surface area of one side of the cube and then multiply it by six. If you want to know how to find the surface area of a cube, just follow these steps.
-
1
Understand that the surface area of a cube is made up of the areas of its six faces. Since all of the faces of a cube are congruent, we can just find the area of one face and multiply it by 6 to get the total surface area. The surface area can be found by using a simple formula: 6 x s2, where «s» represents a side of the cube.[1]
-
2
Find the area of one side of the cube. To find the area of one side of the cube, you need to find «s,» which represents the side length of a cube, and then find s2. This really means that you’ll be multiplying the length of the cube’s side times its width to find its area — the length and width of a cube’s side just happen to be the same. If one side of the cube, or «s,» is equal to 4 centimeter (1.6 in), then the area of the side of the cube is (4 cm)2, or 16 cm2. Remember to state your answer in square units.[2]
Advertisement
-
3
Multiply the area of the side of the cube by 6. Now that you’ve found the area of one side of the cube, all you have to do to find the surface area is to multiply this number by 6. 16 cm2 x 6 = 96 cm2. The surface area of the cube is 96 cm2.[3]
Advertisement
-
1
Find the volume of the cube. Let’s say that the volume of the cube is 125 cm3.[4]
-
2
Find the cube root of the volume. To find the cube root of the volume, just look for a number that can be cubed to become the volume, or use your calculator. The number won’t always be a whole number. In this case, with the number 125 is a perfect cube, and its cube root is 5, because 5 x 5 x 5 = 125. So, «s,» or one side of the cube, is 5.[5]
-
3
Plug this answer into the formula for finding the surface area of a cube. Now that you know the length of one side of a cube, just plug it into the formula for finding the surface area of a cube: 6 x s2. Since the length of one side is 5 centimeter (2.0 in), just plug it into the formula like this: 6 x (5 cm)2.[6]
-
4
Solve. Just do the math. 6 x (5 cm)2 = 6 x 25 cm2 = 150 centimeter (59.1 in) 2.
Advertisement
Add New Question
-
Question
What if the cube has different lengths — for example 3 cm, 4 cm and 3 cm?
All cubes have equal sides. If they aren’t equal, they are call rectangular prisms.
-
Question
How do I find the total surface area of a cube whose volume is 3?
You would have to refer to a table that gives cube roots, because the formula for finding the surface area of this cube is six times the cube root of 9.
-
Question
How do I find the volume of the cube if I only know the surface area?
Divide the surface area by 6. That gives you the area of one side. Find the square root of that area. That gives you the length of one edge. Cube that number. That’s the volume (in cubic units).
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
About This Article
Article SummaryX
To find the surface area of a cube, use the formula: surface area = 6s^2, where s is the length of one of the sides. If you don’t know the length of the sides, you can find the surface area using volume. Just find the cube root of the volume, which is equal to the length of one side of the cube. Then, plug that number into the formula for finding the surface area. For examples you can work through, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 445,863 times.