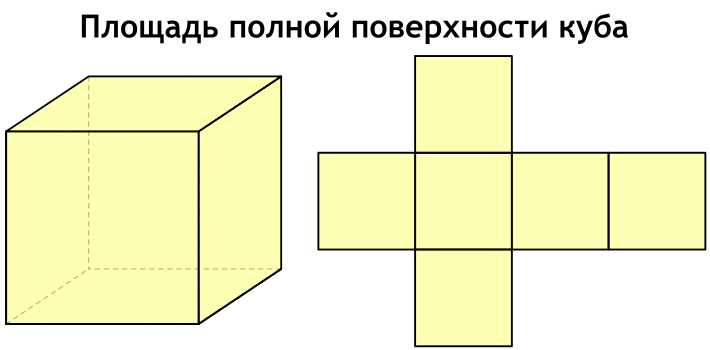
В данной публикации мы рассмотрим, как можно найти площадь поверхности куба и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади куба
- 1. Через длину ребра
- 2. Через длину диагонали грани
- Примеры задач
Формула вычисления площади куба
1. Через длину ребра
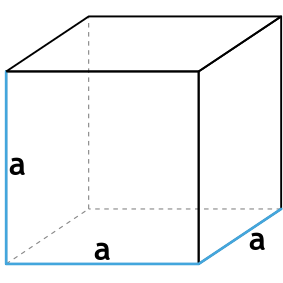
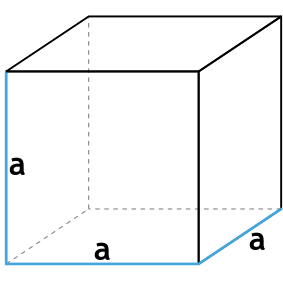
Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате.
S = 6 ⋅ a2
Данная формула получена следующим образом:
- Куб – это правильная геометрическая фигура, все грани которого являются равными квадратами с длиной стороны a (одновременно является ребром куба).
- Площадь каждой грани считается так: S = a ⋅ a = a2.
- Всего у куба 6 граней, а значит, площадь его поверхности равняется шести площадям одной грани: S = 6 ⋅ a2.
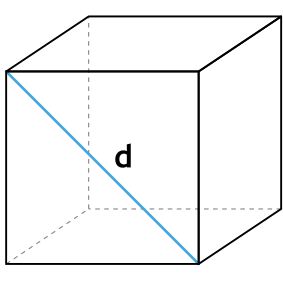
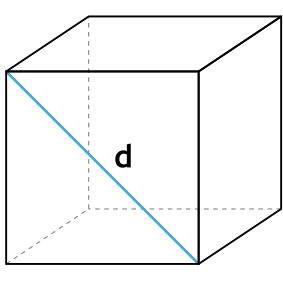
2. Через длину диагонали грани
Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√2.
Это значит, что вычислить площадь поверхности фигуры можно так:
S = 6 ⋅ (d/√2)2
Примеры задач
Задание 1
Найдите площадь поверхности куба, если длина его ребра составляет 12 см.
Решение:
Используем первую формулу выше и получаем:
S = 6 ⋅ (12 см)2 = 864 см2.
Задание 2
Площадь поверхности куба равняется 294 см2. Вычислите длину его ребра.
Решение:
Примем ребро куба за a. Из формулы расчета площади следует:
Задание 3
Вычислите площадь поверхности куба, если диагональ его грани равняется 5 см.
Решение:
Воспользуемся формулой, в которой задействована длина диагонали:
S = 6 ⋅ (5 см : √2)2 = 75 см2.
Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.
Онлайн-калькулятор площади поверхности куба
У куба есть двенадцать ребер, то есть, отрезков, которые являются сторонами квадратов.
Также он имеет восемь вершин и шесть граней.
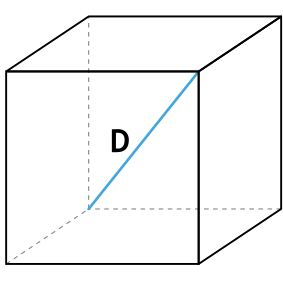
У куба есть диагональ, соединяющая противоположные вершины.
Формула площади поверхности куба
Площадь поверхности куба – это сумма площадей всех его граней:
S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6
Площадь каждой грани одинакова, то есть:
S1=S2=S3=S4=S5=S6=S′S_1=S_2=S_3=S_4=S_5=S_6=S’
S′S’ — площадь любой грани куба.
Тогда полная площадь поверхности куба запишется как:
S=6⋅S′S=6cdot S’
Рассмотрим на примерах разные способы вычисления полной площади поверхности куба.
Формула площади поверхности куба по длине ребра куба
Площадь каждой грани куба вычисляется как площадь квадрата, со стороной ребра куба по формуле:
S′=a⋅a=a2S’=acdot a=a^2
aa — сторона куба.
Отсюда, окончательно площадь поверхности куба:
S=6⋅a2S=6cdot a^2
aa — длина стороны куба.
Найти площадь поверхности куба, если длина его ребра равна 12 (см.).
Решение
a=12a=12
S=6⋅a2=6⋅122=6⋅144=864S=6cdot a^2=6cdot 12^2=6cdot 144=864 (см. кв.)
Ответ: 864 см. кв.
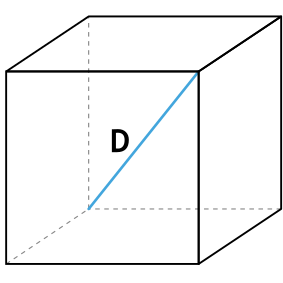
Формула площади поверхности куба по диагонали куба
По теореме Пифагора, диагональ куба связанна с длиной его ребра по формуле:
d2=a2+a2+a2d^2=a^2+a^2+a^2
d2=3⋅a2d^2=3cdot a^2
d=3⋅ad=sqrt{3}cdot a
Отсюда:
a=d3a=frac{d}{sqrt{3}}
Подставим в формулу для площади:
S=6⋅a2=6⋅(d3)2=2⋅d2S=6cdot a^2=6cdotBig(frac{d}{sqrt{3}}Big)^2=2cdot d^2
S=2⋅d2S=2cdot d^2
dd — диагональ куба.
Одна четвертая часть диагонали куба равна 2 (см.). Найти площадь поверхности куба.
Решение
14⋅d=2frac{1}{4}cdot d=2
Найдем диагональ:
d=4⋅2=8d=4cdot 2=8
Площадь:
S=2⋅d2=2⋅82=2⋅64=128S=2cdot d^2=2cdot 8^2=2cdot 64=128 (см. кв.)
Ответ: 128 см. кв.
Формула площади поверхности куба по длине диагонали квадрата (грани куба)
По теореме Пифагора, диагональ квадрата ll связанна с его стороной aa:
l2=a2+a2l^2=a^2+a^2
l2=2⋅a2l^2=2cdot a^2
l=2⋅al=sqrt{2}cdot a
Тогда сторона квадрата:
a=l2a=frac{l}{sqrt{2}}
Подставляем в формулу для площади и получаем:
S=6⋅a2=3⋅l2S=6cdot a^2=3cdot l^2
S=3⋅l2S=3cdot l^2
ll — диагональ квадрата (грани куба).
Одна четвертая часть диагонали квадрата равна 1 (см). Найти площадь поверхности куба, образованного данным четырехугольником.
Решение
14⋅l=1frac{1}{4}cdot l=1
Найдем диагональ квадрата:
l=4⋅1=4l=4cdot 1=4
Тогда площадь:
S=3⋅l2=3⋅42=48S=3cdot l^2=3cdot 4^2=48 (см. кв.)
Ответ: 48 см. кв.
Разберем более сложные примеры.
Формула площади поверхности куба по площади вписанного в куб шара
В куб вписан шар площади SшарS_{text{шар}}. Тогда радиус RR этого шара равен половине длины стороны куба aa:
R=a2R=frac{a}{2}
Площадь шара дается формулой:
Sшар=4⋅π⋅R2S_{text{шар}}=4cdotpicdot R^2
Отсюда найдем радиус шара:
R=Sшар4⋅πR=sqrt{frac{S_{text{шар}}}{4cdotpi}}
Сторона грани куба:
a=2⋅R=2⋅Sшар4⋅πa=2cdot R=2cdotsqrt{frac{S_{text{шар}}}{4cdotpi}}
Наконец площадь поверхности куба:
S=6⋅a2=6⋅SшарπS=6cdot a^2=frac{6cdot S_{text{шар}}}{pi}
S=6⋅SшарπS=frac{6cdot S_{text{шар}}}{pi}
SшарS_{text{шар}} — площадь шара, вписанного в куб.
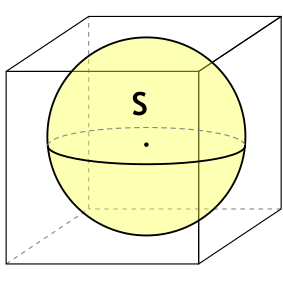
В куб вписан шар, площадь которого равна 64 “пи” (см. кв.). Найти полную площадь поверхности куба.
Решение
Sшар=64πS_{text{шар}}=64pi
По формуле:
S=6⋅Sшарπ=6⋅64⋅ππ=384S=frac{6cdot S_{text{шар}}}{pi}=frac{6cdot 64cdotpi}{pi}=384 (см. кв.)
Ответ: 384 см. кв.
Не знаете, кто сможет решить контрольную работу на заказ для вас? Наши эксперты с удовольствием окажут вам помощь!
Тест по теме “Площадь поверхности куба”
Формулы?
Площадь поверхности куба равна сумме площадей шесть квадратов, которые и составляют поверхность куба.
Площадь каждого такого квадрата, которые являются гранями данного куба, вычисляются по формуле:
, где а — длина ребра квадрата.
Чтобы найти площадь всей поверхности квадрата, надо найти сумму площадей всех шести его граней или просто, умножить площадь одной из граней на 6.
Вот так можно вывести формулу вычисления площади поверхности куба:
модератор выбрал этот ответ лучшим
Турук Макто
[55.6K]
9 лет назад
Я формул не помню, если они специально какие-то есть. Но давайте по логике. Если сторона одна — это квадрат, то сторона умножается на сторону — это будет площадь квадрата. И таких квадратов шесть штук. Вот собственно и всё. Сторона в квадрате шесть раз! 6*а*а.
MarkTolkien
[85.3K]
9 лет назад
Для того, чтобы найти площадь поверхности куба, нужно вычислить площадь грани. Площадь одной грани — длина ребра в квадрате, то есть во второй степени. У куба шесть сторон (граней), поэтому площадь одной множим на 6.
Ракитин Сергей
[450K]
9 лет назад
У куба шесть граней, каждая из которых представляет собой квадрат. Если сторона куба равна a, то площадь его поверхности будет равна 6a^2. В справочниках эту формулу обычно не приводят в силу её очевидности.
Асюшка
[101K]
9 лет назад
Так как грани куба — это квадраты. И куб состоит из шести таких граней, то получается, что чтобы найти площадь поверхности куба, нам необходимо для начала найти площадь квадрата(грани куба) умножаем на 6 (6 граней). Ой, сейчас сама запутаюсь и Вас запутаю, проще, действительно, формулой записать:
S (площадь куба) = 6 * а2 (площадь одной грани — квадрата).
Медвед
[141K]
9 лет назад
Куб — это параллелепипед, у которого все стороны равны. Значит, каждая из граней куба является квадратом, и все эти квадраты равны между собой. Если обозначить сторону куба как Н, площадь одного квадрата будет (Н)в квадрате. Таких квадратов 6. Поэтому имеем формулу для определения поверхности куба S:
S=6x[(Н)в квадрате]
Samborskaya
[7K]
9 лет назад
Площадь поверхности куба складывается из всех площадей его сторон. Каждая сторона представляет из себя квадрат, а площадь квадрата равна произведению его сторон. Пусть сторона квадрата равна Х, тогда площадь всей поверхности куба вычисляется как S = 6 * X * X.
Любовь7800
[4K]
9 лет назад
И без формул даже можно, если нужно измерить все поверхности, то найти площать одной, умножив одну сторону на другую и потом умножить на шесть. Так ка у куда все стороны равны, то можно одну сторону умножить сразу на 12, так как граней 12.
Радуга-Весна
[50.5K]
9 лет назад
Площадь поверхности куба равняется шесть умножить на квадрат длины грани куба.
А вот и сама формула площади куба
S = 6* a2
S — это площадь куба,
a — это длина грани куба.
Как видно площадь куба рассчитывается совсем просто.
Solnce lychik
[40.9K]
9 лет назад
Эту площадь учили еще в школе. А формула выглядит так:
s=6*a2
где s-площадь куба
a-длина грани
Если честно без интернета я бы это и не вспомнила.
Да все что учила в школе со временем забывается. А вспомнить очень сложно.
Знаете ответ?

{S_{полн}=6a^2}
На этой странице мы собрали формулы, которые помогут найти площадь полной и боковой поверхности куба. А чтобы упростить расчет у нас есть калькулятор, который сделает это быстро и точно.
В дополнение на сайте можно найти объем куба.
Куб — фигура, представляющая собой правильный многогранник, все грани которого являются квадратами. Все ребра (стороны) куба равны между собой.
Содержание:
- калькулятор площади поверхности куба
- площадь полной поверхности куба
- формула площади полной поверхности куба через ребро
- формула площади полной поверхности куба через диагональ грани
- формула площади полной поверхности куба через диагональ куба
- формула площади полной поверхности куба через периметр грани
- формула площади полной поверхности куба через периметр куба
- формула площади полной поверхности куба через объем
- формула площади полной поверхности куба через площадь вписанного шара
- площадь боковой поверхности куба
- формула площади боковой поверхности куба через ребро
- формула площади боковой поверхности куба через диагональ грани
- формула площади боковой поверхности куба через диагональ куба
- формула площади боковой поверхности куба через периметр грани
- формула площади боковой поверхности куба через периметр куба
- формула площади боковой поверхности куба через объем
- примеры задач
Что такое площадь полной поверхности куба
Куб состоит из сторон, которые называют гранями. Каждая такая грань представляет собой квадрат, а всего у куба 6 граней. Площади всех этих граней равны между собой и сложив все площади всех шести граней куба мы получим площадь полной поверхности куба.
Площадь полной поверхности куба – это сумма площадей всех его граней.
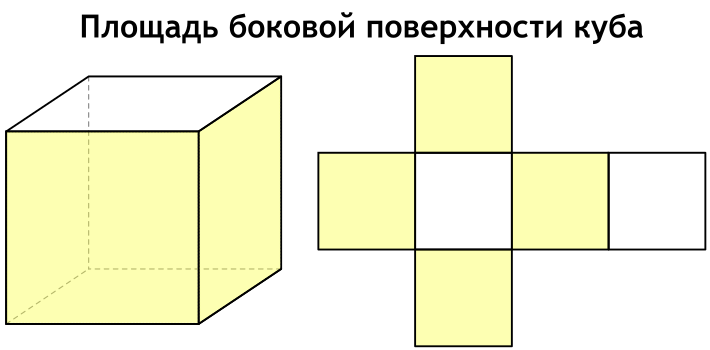
Площадь полной поверхности удобно представить, если посмотреть на развертку куба.
Формула площади полной поверхности куба через ребро
{S_{полн}=6a^2}
a — ребро куба
Формула площади полной поверхности куба через диагональ грани
{S_{полн}=3d , ^2}
d — диагональ грани куба
Формула площади полной поверхности куба через диагональ куба
{S_{полн}=2D^2}
D — диагональ куба
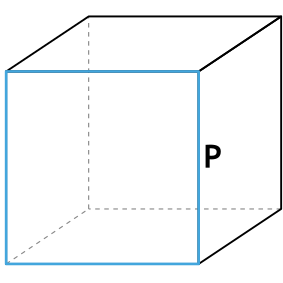
Формула площади полной поверхности куба через периметр грани
{S_{полн}= dfrac{3}{8}P^2}
P — периметр грани куба
Формула площади полной поверхности куба через периметр куба
{S_{полн}= dfrac{P^2}{24}}
P — периметр куба
Формула площади полной поверхности куба через объем
{S_{полн}= 6{(sqrt[3]{V})}^2}
V — объем куба
Формула площади полной поверхности куба через площадь вписанного шара
{S_{полн}= 6 dfrac{S}{pi}}
S — площадь вписанного в куб шара
Что такое площадь боковой поверхности куба
Боковая поверхность куба — сумма площадей всех его боковых граней, которых у куба четыре.
Формула площади боковой поверхности куба через ребро
{S_{бок} = 4a^2}
a — ребро куба
Формула площади боковой поверхности куба через диагональ грани
{S_{бок}=2d , ^2}
d — диагональ грани куба
Формула площади боковой поверхности куба через диагональ куба
{S_{бок}=dfrac{4}{3}D^2}
D — диагональ куба
Формула площади боковой поверхности куба через периметр грани
{S_{бок}= dfrac{P^2}{4}}
P — периметр грани куба
Формула площади боковой поверхности куба через периметр куба
{S_{бок}= dfrac{P^2}{36}}
P — периметр куба
Формула площади боковой поверхности куба через объем
{S_{бок}= 4{(sqrt[3]{V})}^2}
V — объем куба
Примеры задач на нахождение площади поверхности куба
Задача 1
Найдите площадь поверхности куба, если его объем равен 125см³.
Решение
Для нахождения площади полной поверхности куба через его объем, нам поможет эта формула.
S_{полн} = 6{(sqrt[3]{V})}^2 = 6{(sqrt[3]{125})}^2 = 6{(5)}^2 = 6 cdot 25 = 150 : см²
Ответ: 150 см²
Проверить ответ нам поможет калькулятор .
Задача 1
Найдите площадь боковой поверхности куба с ребром 4см.
Решение
Для нахождения площади боковой поверхности куба с известной длиной ребра используем эту формулу.
S_{бок} = 4a^2 = 4 cdot 4^2 = 4 cdot 16 = 64 : см²
Ответ: 64 см²
Проверка .
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое калькулятор площади поверхности куба?
Калькулятор площади поверхности куба — это онлайн инструмент, который помогает вычислить площадь всех граней куба, исходя из различных параметров, таких как длина ребра, диагонали куба и диагонали сторон.
Калькулятор рассчитывает площадь с использованием следующих формул:
По длине ребра
Если известна длина ребра куба (a), площадь поверхности куба может быть вычислена по формуле:
S = 6a²
Здесь «S» обозначает площадь поверхности, а «a» — длину ребра.
По диагонали куба
Если известна длина диагонали куба (D), площадь поверхности также может быть вычислена. Длина ребра куба (a) связана с длиной диагонали куба по формуле: a = Dd/√3. Затем площадь поверхности может быть вычислена с использованием формулы из предыдущего пункта:
S = 6(D/√3)²
По диагоналям сторон
Если известны длины диагоналей сторон куба (d), то площадь поверхности может быть вычислена по формуле:
S = 6(d/√2)²
Куб и его свойства
Куб — это особый вид геометрического тела, принадлежащий к классу правильных многогранников. Рассмотрим подробнее его особенности:
- Грани. Куб имеет шесть граней. Все грани куба являются квадратами и имеют одинаковую форму и размер. Каждая грань параллельна и перпендикулярна другим граням.
- Ребра. Куб имеет двенадцать ребер. Ребра куба соединяют вершины и определяют его форму. Все ребра куба имеют одинаковую длину. Каждое ребро сопряжено с двумя гранями.
- Вершины. Куб имеет восемь вершин. Вершины — это точки пересечения ребер. Каждая вершина сопряжена с тремя ребрами.
- Диагонали. Куб имеет четыре пространственные диагонали. Пространственные диагонали соединяют противоположные вершины куба. Диагонали являются отрезками, которые находятся внутри куба.
- Периметр. Периметр куба — это сумма длин всех его ребер. Так как куб имеет одинаковые ребра, то периметр равен шести умноженному на длину ребра.
- Объем. Объем куба вычисляется путем возведения длины ребра в куб. Все объемы его шести граней равны между собой. Объем куба определяет, сколько пространства он занимает.
- Площадь поверхности. Площадь поверхности куба вычисляется умножением площади одной грани на шесть. Площадь каждой грани равна длине стороны куба, возведенной в квадрат.
Куб является одним из наиболее простых и симметричных геометрических тел. Его правильная форма и уникальные свойства делают его важным объектом изучения в математике и геометрии.
Прикладное применение куба
Кубы и концепции, связанные с ними, применяются в различных областях. Рассмотрим несколько примеров:
- Геометрия. Кубы являются одним из основных объектов изучения в геометрии. Они помогают понять концепции объема, площади поверхности, диагоналей и углов. Кубы используются для решения геометрических задач и развития пространственного мышления.
- Архитектура. В архитектуре кубы используются для создания 3D-моделей зданий и других конструкций. Они могут служить основой для проектирования фасадов, интерьеров и пространств. Кубические формы могут добавлять структуру и гармонию в архитектурные проекты.
- Механика и инженерия. Кубы и их производные формы (например, параллелепипеды) используются в механике и инженерии для моделирования и проектирования объектов. Они могут помочь в определении объемов, массы и распределения материала в различных инженерных конструкциях.
- Образование. Кубы используются в учебных заведениях для обучения геометрии и пространственной геометрии. Они помогают студентам лучше понять и визуализировать трехмерные концепции и связанные с ними математические принципы.
- Игры и развлечения. Кубы в виде игральных костей или пазлов широко используются в играх и развлекательных активностях. Они предоставляют возможность развивать логическое мышление, способствуют развлечению и создают пространство для креативности.
Это лишь несколько примеров областей, где кубы могут быть применены. Кубическая форма широко используется во многих сферах человеческой деятельности, благодаря своей простоте и универсальности.
Для чего может понадобиться вычисление площади поверхности куба?
Вычисление площади поверхности куба может быть полезным во многих ситуациях, включая:
- Инженерия и строительство. При проектировании зданий или конструкций, где кубические формы присутствуют, вычисление площади куба может помочь определить необходимое количество материала, такого как облицовочные панели, краска или обои, для покрытия его поверхности.
- Упаковка и логистика. Вычисление площади куба может быть полезным для определения объема или площади поверхности упаковочных контейнеров или коробок. Это помогает в оптимизации использования пространства при упаковке товаров или грузов для транспортировки или хранения.
- Дизайн интерьера и мебели. При планировании интерьера или разработке мебели с кубическими элементами, вычисление площади куба может помочь определить размеры и количество материала, необходимого для отделки поверхности или создания декоративных элементов.
- Геометрия и математика. Вычисление площади куба может быть использовано в учебных задачах или исследованиях в геометрии и математике. Это помогает учащимся понять связь между размерами сторон куба и его площадью поверхности, а также развить навыки в вычислении площадей различных геометрических фигур.
- Компьютерная графика и 3D-моделирование. В визуализации и моделировании трехмерных объектов, вычисление площади куба может быть полезным при определении его свойств и текстурных координат для правильного отображения на экране или в симуляциях.
Вычисление площади куба является одной из основных операций, которая позволяет анализировать его характеристики и применять их в практических ситуациях в различных областях.
Рассмотрим подробный пример
Предположим, у вас есть задача по шумоизоляции комнаты в доме. Вы хотите установить звукоизоляционные панели на стены, чтобы уменьшить проникновение звука извне и избежать перекрестного шума между помещениями.
Шаг 1. Измерьте длину ребра куба.
Измерьте длину одного ребра куба, которую вы хотите покрыть звукоизоляционными панелями. Предположим, длина ребра составляет 3 метра.
Шаг 2. Вычислите площадь поверхности куба.
Используйте формулу для вычисления площади поверхности куба: S = 6a², где S — площадь поверхности, a — длина ребра.
Подставьте значения в формулу:
S = 6 * 3² = 6 * 9 = 54 квадратных метра.
Таким образом, площадь поверхности куба составляет 54 квадратных метра.
Шаг 3. Определите количество звукоизоляционных панелей.
Определите площадь покрытия одной звукоизоляционной панели. Предположим, одна панель покрывает 2 квадратных метра поверхности.
Рассчитайте количество панелей, необходимых для покрытия всей площади поверхности куба:
Количество панелей = Площадь поверхности куба / Площадь покрытия одной панели
Количество панелей = 54 / 2 = 27 панелей.
Таким образом, для шумоизоляции помещения в доме с кубической формой, вам потребуется 27 звукоизоляционных панелей.
Этот пример показывает, как вычисление площади поверхности куба может быть полезным при планировании и определении необходимого количества материалов для шумоизоляции помещения.
❓ Вопросы и ответы
Вот несколько вопросов и ответов, связанных с калькулятором вычисления площади поверхности куба.
Что такое калькулятор вычисления площади поверхности куба?
Калькулятор вычисления площади поверхности куба — это онлайн инструмент, который позволяет автоматически вычислить площадь поверхности куба на основе введенных параметров, таких как длина ребра, диагональ куба или диагонали его сторон.
Как использовать калькулятор для вычисления площади поверхности куба?
Для использования калькулятора вычисления площади поверхности куба вам нужно ввести известные параметры, такие как длина ребра, диагональ куба или диагонали сторон, в соответствующие поля калькулятора. Затем нажмите кнопку «Рассчитать», и калькулятор автоматически вычислит и покажет площадь поверхности куба.
Можно ли использовать калькулятор для вычисления площади поверхности куба с десятичными значениями?
Да, калькуляторы для вычисления площади поверхности куба обычно поддерживают десятичные значения. Вы можете вводить длину ребра, диагональ или диагонали куба с десятичными числами для получения точных результатов.
В каких единицах измерения будет выведен результат площади поверхности куба?
Результат площади поверхности куба будет выведен в квадратных единицах измерения, соответствующих используемой системе измерений (например, квадратные метры, квадратные футы и т. д.).
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии