Как найти площадь поверхности многогранника вершинами которого - Исправление недочетов и поиск решений вместе с Examum.ru

07
Сен 2013

Категория: 02 Стереометрия

02. Составные многогранники. Площадь поверхности. Объем

2013-09-07
2022-09-11

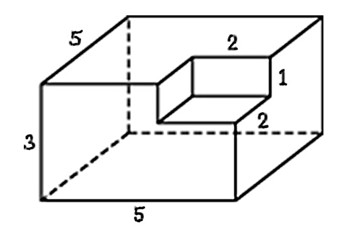
Задача 1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение: + показать

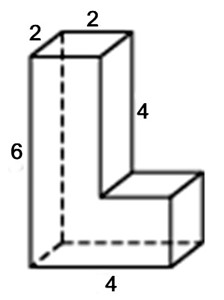
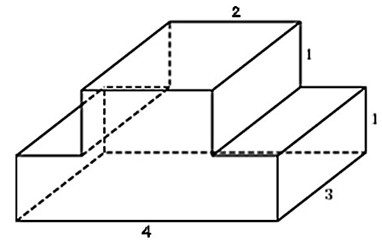
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение: + показать

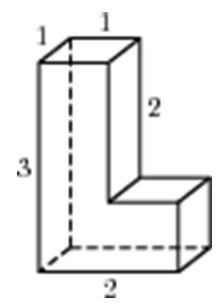
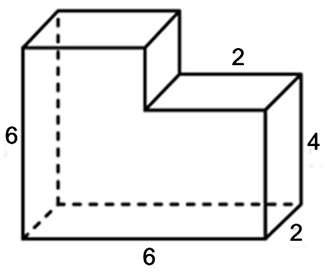
Задача 3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение: + показать

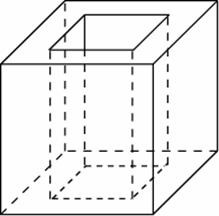
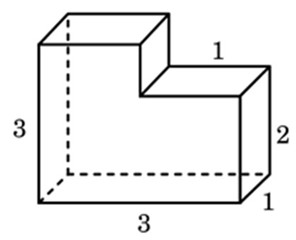
Задача 4. Из единичного куба вырезана правильная четырехугольная призма со стороной основания и боковым ребром Найдите площадь поверхности оставшейся части куба.

Решение: + показать

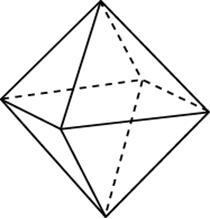
Задача 5. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в раз?

Решение: + показать

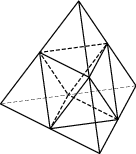
Задача 6. Площадь поверхности тетраэдра равна Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра Видео*

pic-1

Решение: + показать

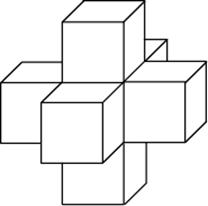
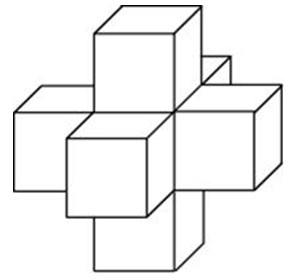
Задача 7. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

Решение: + показать

Задача 8. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

pic-2

Решение: + показать

Задача 9. Объем тетраэдра равен Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.

pic-1

Решение: + показать

Задача 10. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы , площадь основания которой равна 3, а боковое ребро равно 7.

xcvb

Решение: + показать

Вы можете пройти тест “Cоставные многогранники”

Автор: egeMax |

комментариев 14

Источник

Формулы объёма и площади поверхности. Многогранники.

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Куб		диагональ
Параллелепипед	$V=S_text{OCH}h, h -$ высота
Прямоугольный параллелепипед		$d=sqrt{a^2+b^2+c^2}$
Призма	$V=S_text{OCH}h$	$S = 2S_text{OCH}+$
Пирамида	$V=frac{1}{3}S_text{OCH}h$	$S = S_text{OCH}+$

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение:

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб

Очевидно, их 6, поскольку у куба 6 граней.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Разберем задачи, где требуется найти площадь поверхности многогранника.

Мы рассмотрим призмы и пирамиды. Начнем с призмы.

Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.

Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.

Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Многогранник на рисунке – это прямая призма с высотой 12.

$P_text{OCH}=8+6+6+2+2+4=28.$

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

(больший квадрат), (маленький прямоугольник), $S_text{OCH}=36+8=44$

Подставим все данные в формулу: и найдем площадь поверхности многогранника:

Ответ: 424.

Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение.

Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:

$P_text{OCH}=4+5+2+1+2+4=18.$

Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:

(большой прямоугольник), $S_text{OCH}=16+2=18$ (маленький прямоугольник).

Найдем площадь полной поверхности:

Ответ: 54

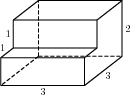
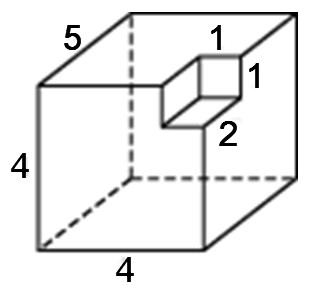
Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Покажем еще один способ решения задачи.

Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.

И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:

Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.

Ответ: 42

Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.

Решение.

Пусть АВ = 5 см, ВС = 3 см, тогда $angle{ABC}=120^{circ}$

Из по теореме косинусов найдем ребро АС:

$AC^2=AB^2+BC^2-2cdot ABcdot BC cdot cos120^{circ}$

$AC^2=25+9-2cdot5cdot3cdotleft(-frac{1}{2}right)=47, ~AC = 7$

Отрезок АС – большая сторона , следовательно, большая боковая грань призмы.

Поэтому или откуда h=5.

Ответ: 75

Теперь две задачи на площадь боковой поверхности пирамиды.

Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.

Решение.

Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.

Проведем , тогда (по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.

– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.

Из прямоугольного получим:

$AK=sqrt{AB^2-BK^2}=sqrt{13^2-5^2}=sqrt{169-25}=sqrt{144}=12.$

Из прямоугольного имеем:

$DK=sqrt{DA^2+AK^2}=sqrt{9^2+12^2}=sqrt{81+144}=sqrt{225}=15.$

(по двум катетам), тогда $S_{ADB}=S_{ADC},$ следовательно

$=2S_{ADB}+S_{BDC},$ $=2cdotfrac{1}{2}cdot13cdot9+frac{1}{2}cdot10cdot15=117+75=192.$

Ответ: 192

Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.

Решение:

Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.

Площадь поверхности пирамиды равна

где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.

Значит, полупериметр основания .

Апофему найдем по теореме Пифагора:

$h=sqrt{37^2-12^2}=sqrt{(37-12)(37+12)}=sqrt{25cdot49}=5cdot7=35$

Ответ: 2256

Как решать задачи на нахождение объема многогранника сложной формы?

Покажем два способа.

Первый способ

1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.

Второй способ.

1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.

Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

1) Достроим составной многогранник до параллелепипеда.

2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:

3) Найдем объем лишней части, то есть маленького параллелепипеда.

Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем

4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:

Ответ: 220.

Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.

Объем призмы равен $V=S_{OCH}cdot h$ , а так как призма прямая, то ее боковое ребро является и высотой, то есть h=6.

Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания

$S_{OCH}=frac{1}{2}cdot ab=frac{1}{2}cdot6cdot7=21.$

Ответ: 126

Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.

Решение.

Объем призмы равен $V = S_{OCH}cdot h$

Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.

Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.

Объем воды не изменился, Так как высота воды h_2 должна быть в 81 раз меньше, чем h_1. Она равна (см).

Ответ: 4

Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды ABDA_1.

Решение.
Опустим из вершины A_1 высоту A_1H Н на основание ABCD.

$=S_{ABCD}cdot A_1H$

$=frac{1}{3}S_{ABD}cdot A_1H$

Диагональ основания делит его на два равных треугольника, следовательно, $S_{ABD}=frac{1}{2}S_{ABCD}.$

Имеем:

$ABDA_1=frac{1}{3}S_{ABD}cdot A_1H=frac{1}{3}cdotfrac{1}{2}S_{ABCD}cdot A_1H=frac{1}{6}V_{ABCDA_1B_1C_1D_1}=frac{1}{6}cdot21=3,5.$

Ответ: 3,5

Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна

Решение.
По формуле объема пирамиды, .

В основании пирамиды лежит правильный треугольник. Его площадь равна $S_{OCH}=frac{a^2sqrt{3}}{4}.$

$S_{OCH}=frac{8^2sqrt{3}}{4}=frac{64sqrt{3}}{4}=16sqrt{3}.$

Объем пирамиды $V=frac{1}{3}cdot16sqrt{3}cdot6sqrt{3}=16cdot6=96.$

Ответ: 96

Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.

Решение.

По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.

Пусть AD=x, тогда $S_{OCH}=x^2.$

Так как точки М и К – середины АD и DС соответственно, то $DM=DK=frac{x}{2}.$

$S_{MDK}=frac{1}{2}MDcdot DK=frac{1}{2}cdotfrac{x}{2}cdotfrac{x}{2}=frac{1}{8}x^2.$

Площадь треугольника MDK, лежащего в основании новой призмы, составляет $frac{1}{8}$ часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: $V=S_{OCH}cdot h$ , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен 32:8=4.

Ответ: 4

Докажем полезную теорему.

Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

Доказательство:

Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.

$S=P_{perp}cdot l.$

Больше задач на формулы объема и площади поверхности здесь.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Площадь поверхности многогранника. В данной рубрике в опубликованных статьях «Общий обзор. Формулы стереометрии« и «Что ещё необходимо знать для решения по стереометрии« мы уже рассмотрели теоретические моменты, которые необходимы для решения.

В составе ЕГЭ по математике имеется целый ряд задач на определение площади поверхности и объема составных многогранников. Это, наверное, одни из самых простых задач по стереометрии. НО! Имеется нюанс. Не смотря на то, что сами вычисления просты, ошибку при решении такой задачи допустить очень легко.

В чём же дело? Далеко не все обладают хорошим пространственным мышлением, чтобы сразу увидеть все грани и параллелепипеды из которых «состоят» многогранники. Даже если вы умеете делать это очень хорошо, можете мысленно сделать такую разбивку, всё-таки следует не торопиться и воспользоваться рекомендациями из этой статьи.

Кстати, пока работал над данным материалом, нашёл ошибку в одной из задач на сайте. Нужна внимательность и ещё раз внимательность, вот так.

Итак, если стоит вопрос о площади поверхности, то на листе в клетку постройте все грани многогранника, обозначьте размеры. Далее внимательно вычисляйте сумму площадей всех полученных граней. Если будете предельно внимательны при построении и вычислении, то ошибка будет исключена.

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Используем оговоренный способ. Он нагляден. На листе в клетку строим все элементы (грани) в масштабе. Если длины рёбер будут большими, то просто подпишите их.

Ответ: 72

Решите самостоятельно:

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Посмотреть решение

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Посмотреть решение

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Посмотреть решение

Ещё задачи 25881, 77155, 77156. В них приведены решения другим способом (без построения), постарайтесь разобраться — что откуда взялось. Также решите уже представленным способом.

* * *

Если требуется найти объём составного многогранника. Разбиваем многогранник на составляющие его параллелепипеды, записываем внимательно длины их рёбер и вычисляем.

Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Объем многогранника, изображенного на рисунке равен сумме объёмов двух многогранников с рёбрами 6,2,4 и 4,2,2

Ответ: 64

Решите самостоятельно:

Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Посмотреть решение

Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

Посмотреть решение

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Посмотреть решение

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Посмотреть решение

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Посмотреть решение

Казалось бы, данные задачи можно вообще не рассматривать, они же просты и понятны. Но в их решении важна практика. Повторюсь, что ошибиться очень легко, попрактикуйтесь с подобными задачами и вы убедитесь.

В открытом банке задач много примеров аналогичных задач (смотрите здесь и здесь). Договоритесь с одноклассниками решить одни и те же задачи, затем сверьтесь.

Мы продолжим рассматривать задачи данной части, не пропустите! Успехов вам!!!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

05
Янв 2012

05 Задание (2022)

Задание 8 (№ 25641) из Открытого банка заданий для подготовки к ЕГЭ по математике.

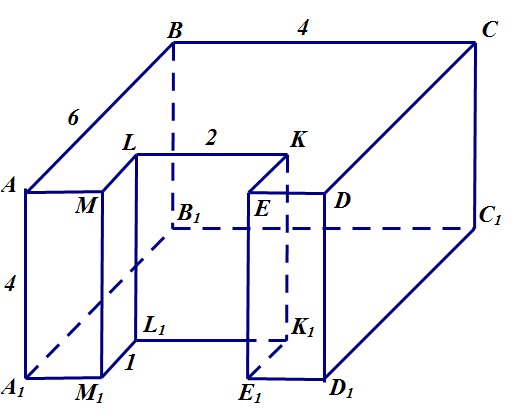
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые)

Решение. Площадь поверхности многогранника равна сумме площадей всех его граней. Так как все грани этого многогранника — прямоугольники, то для нахождения площади каждой грани мы используем формулу площади прямоугольника:

S=ab, где a и b — длины двух смежных сторон прямоугольника.

Обозначим вершины многогранника:

1.Найдем сначала площадь боковой поверхности. Для этого, чтобы не пропустить ни одной грани, обойдем наш многогранник по часовой стрелке, и запишем площадь каждой грани:

S_бок=A₁ABB₁+B₁CC₁+C₁CDD₁+D₁DEE₁+E₁EKK₁+K₁KLL₁+L₁LMM₁+M₁MAA₁.

S_бок=4×6+4×4+4×6+4×1+4×1+4×2+4×1+4×1=88

2. Найдем площадь верхней грани. Для этого из площади прямоугольника ABCD вычтем площадь прямоугольника MLKE:

6х4 — 2×1=22

3. Площадь нижней грани равна площади верхней грани и равна 22.

4. Сложим получившиеся площади: 88+22+22=132.

Ответ: 132.

Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачать

Firefox

|
Отзывов (10)
| Метки: решение задния В11

Источник

Практикум по теме «Площадь поверхности составного многогранника»
15 января 2020 г. 11 класс

Цель: практическое закрепление ЗУН.

Задачи из открытого банка задач.

1. Задание 8 № 25541

Найдите площадь поверхности
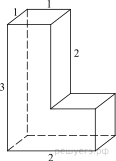
многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади
поверхности прямоугольного параллелепипеда с ребрами 2, 3, 1 и двух площадей
прямоугольников со сторонами 2, 1:

Ответ: 18.

2. Задание 8 № 25561

Найдите площадь
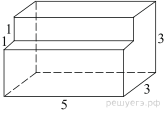
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади
поверхности прямоугольного параллелепипеда с ребрами 3, 3, 5 и двух площадей
квадратов со стороной 1:

Ответ: 76.

3. Задание 8 № 25581

Найдите площадь поверхности
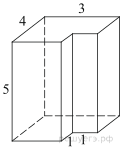
многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади
поверхности прямоугольного параллелепипеда с ребрами 3, 4, 5 и площади двух
квадратов со стороной 1:

Ответ: 92.

4. Задание 8 № 25601

Найдите площадь
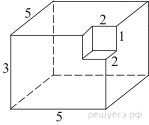
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна площади
поверхности прямоугольного параллелепипеда с ребрами 3, 5, 5:

Ответ: 110.

5. Задание 8 № 25621

Найдите площадь
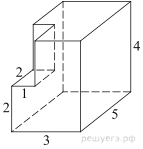
поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна площади
поверхности прямоугольного параллелепипеда с ребрами 3, 5, 4:

Ответ: 94.

Примечание для тех, кто не верит в это решение.

Посчитайте площадь поверхности, сложив площади всех девяти граней
данного многогранника, и смиритесь:

6. Задание 8 № 25641

Найдите площадь
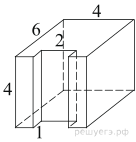
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

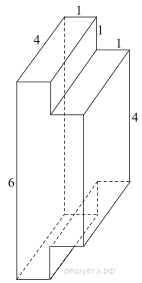
Площадь поверхности заданного многогранника равна сумме площадей
поверхности прямоугольного параллелепипеда с ребрами 6, 4, 4 и двух
прямоугольников со сторонами 1 и 4, уменьшенной на площадь двух прямоугольников
со сторонами 1 и 2:

Ответ: 132.

7. Задание 8 № 25661

Найдите площадь
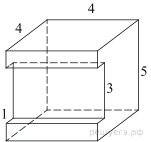
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
поверхности прямоугольного параллелепипеда с ребрами 4, 4, 5 и двух
прямоугольников со сторонами 1 и 4, уменьшенной на площадь двух прямоугольников
со сторонами 1 и 3:

Ответ: 114.

8. Задание 8 № 25681

Найдите площадь поверхности
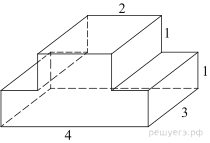
многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
прямоугольников со сторонами 1, 3, 4 и 1, 2, 3, уменьшенной на удвоенную
площадь прямоугольника со сторонами 2, 3:

Ответ: 48.

9. Задание 8 № 25701

Найдите площадь поверхности многогранника, изображенного на
рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
параллелепипедов с ребрами 1, 6, 4 и 1, 4, 4 уменьшенной на удвоенную площадь
квадрата стороной 4:

Ответ: 84.

Приведем другое решение

Площадь поверхности заданного многогранника равна площади
прямоугольного параллелепипеда с ребрами 6, 4, 2 уменьшенной на 4 площади
квадратов со стороной 1:

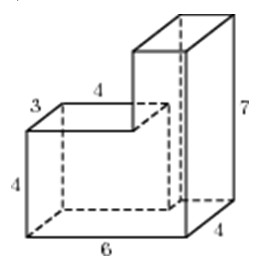
10. Задание 8 № 25721

Найдите площадь
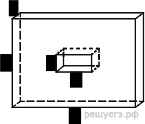
поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
большого и маленького параллелепипедов с ребрами 1, 5, 7 и 1, 1, 2, уменьшенной
на 4 площади прямоугольника со сторонами 1, 2 — передней грани маленького
параллелепипеда, излишне учтенной при расчете площадей поверхности
параллелепипедов:

Ответ: 96.

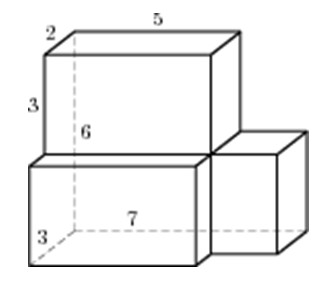
11. Задание 8 № 25881

Найдите площадь
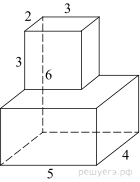
поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей
параллелепипедов со сторонами 2, 3, 3 и 5, 4, 3 уменьшенной на удвоенную
площадь прямоугольника со сторонами 3, 2:

Ответ: 124.

12. Задание 8 № 27071

Найдите площадь
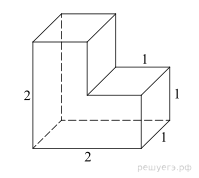
поверхности многогранника, изображенного на рисунке, все двугранные углы
которого прямые.

Решение.

Площадь поверхности заданного многогранника складывается из
четырех площадей квадратов со стороной 1, двух прямоугольников со сторонами 1 и
2 и двух граней (передней и задней), площади которых в свою очередь
складываются из трех единичных квадратов каждая. Всего 4 + 4 + 6 = 14.

Ответ: 14.

13. Задание 8 № 27158

Найдите площадь
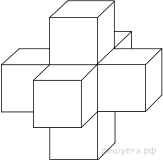
поверхности пространственного креста, изображенного на рисунке и составленного
из единичных кубов.

Решение.

Поверхности креста составлена из шести поверхностей кубов, у
каждого из которых отсутствует одна грань. Тем самым, поверхность креста
состоит из 30 единичных квадратов, поэтому ее площадь равна 30.

Ответ: 30.

14. Задание 8 № 77155

Найдите площадь
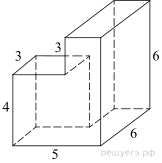
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности данного многогранника равна сумме площадей
поверхностей прямоугольных параллелепипедов с рёбрами 6, 6, 2 и 3, 3, 4,
уменьшенной на две площади прямоугольников со сторонами 3 и 4:

Ответ: 162.

15. Задание 8 № 77156

Найдите площадь
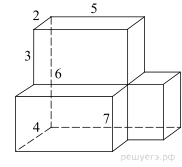
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности тела равна сумме поверхностей трех
составляющих ее параллелепипедов с ребрами 2, 5, 6; 2, 5, 3 и 2, 2,
3, уменьшенная на удвоенные площади прямоугольников со сторонами 5 ,3 и 2, 3:

Ответ: 156.

16. Задание 8 № 77157

Найдите площадь
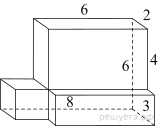
поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности тела равна сумме поверхностей трех
составляющих его параллелепипедов с измерениями 2, 4, 6; 1, 6, 2 и 2, 2, 2:

Ответ: 152.

17. Задание 8 № 512330

Найдите площадь
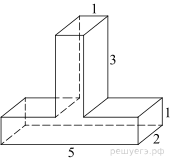
поверхности многогранника, изображённого на рисунке (все двугранные углы
прямые).

Решение.

Площадь поверхности данного многогранника складывается из площадей
двух параллелепипедов со сторонами 1, 3, 2 и 1, 2, 5 за вычетом двух площадей
прямоугольников со сторонами 2 и 1, которые учитываются дважды в представленном
многограннике:

Ответ: 52

Источник