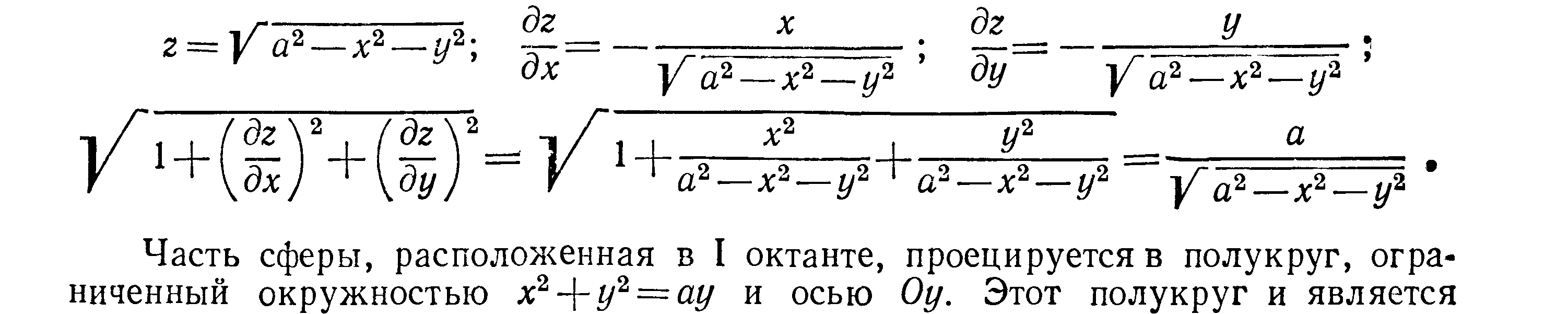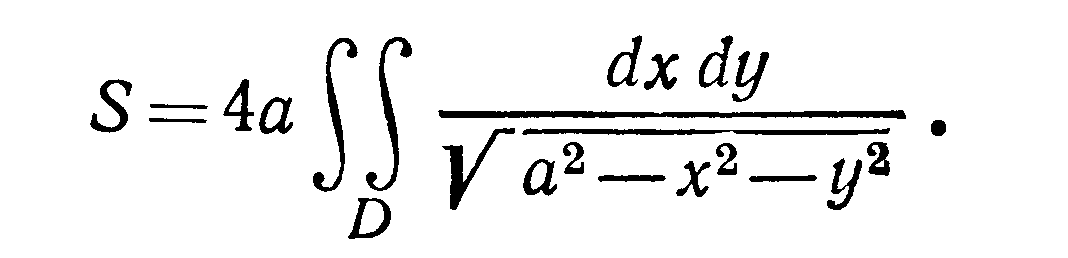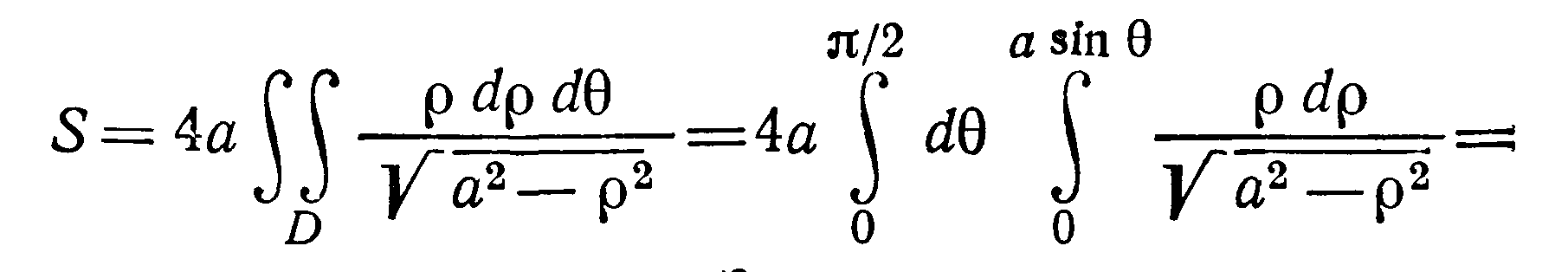Как найти площадь поверхности параболоида - Исправление недочетов и поиск решений вместе с Examum.ru

Площадь поверхности параболоида вращения — это сумма площадей основания и боковой поверхности параболоида.

Параболоид вращения — это поверхность, образующаяся при вращении параболы вокруг её оси симметрии.

Обозначения

Введём обозначения:

H — высота параболоида вращения;

R — радиус основания;

p — фокальный параметр;

y²=2px — каноническое уравнение параболы;

2px=y²+z² — уравнение параболоида вращения;

S_осн — площадь основания радиуса R;

S_{бок.параб} — площадь боковой поверхности;

S_параб — площадь поверхности параболоида вращения c высотой H.

Формула

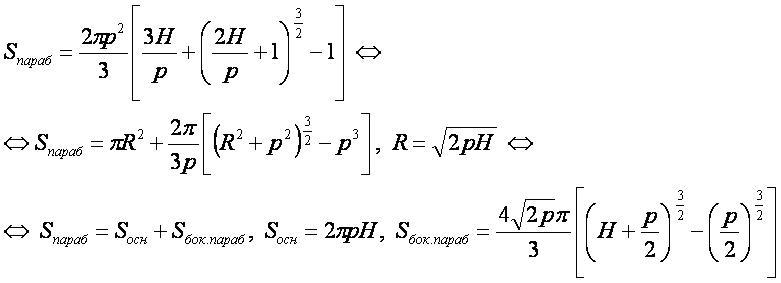
Вывод формулы

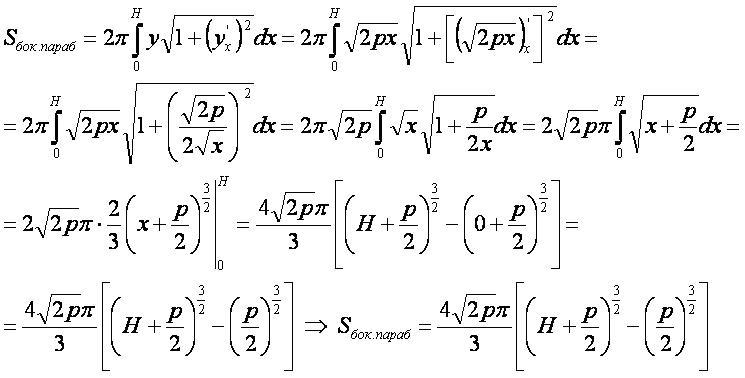
Для вывода используется формула 1 «площадь поверхности фигуры вращения».

Другие фигуры:

Ссылки

Участник:Logic-samara

Источник

Задачи с решениями

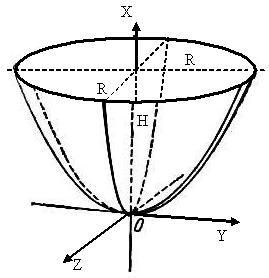
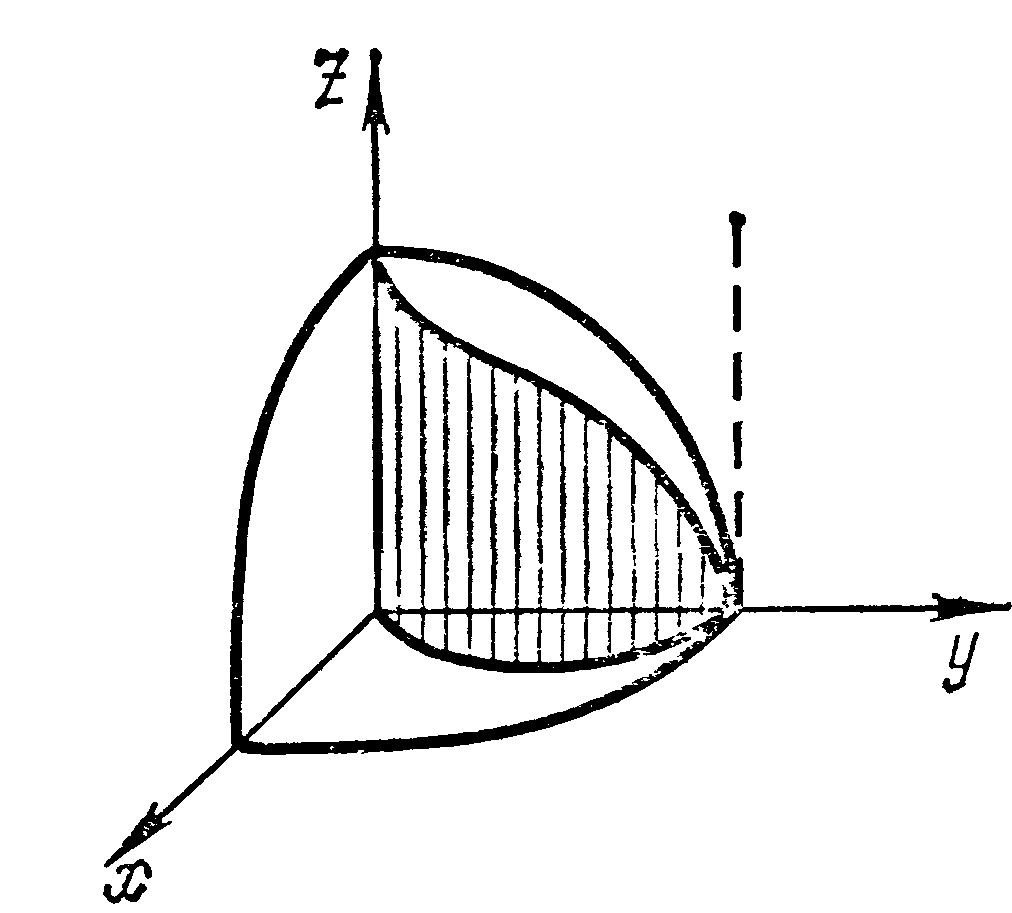
Найти площадь части сферы

заключенной внутри цилиндра

Решение Из уравнения сферы имеем
(для I октанта):

областью интегрирования D.
Поверхность расположена в четырех
октантах потому искомая площадь

Перейдем к полярным координатам, тогда
уравнение окружности примет вид

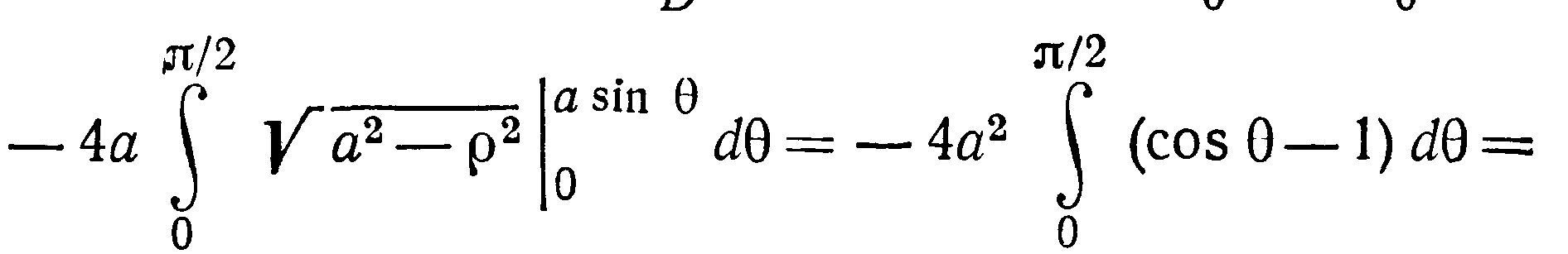
Найти площадь части конуса

внутри цилиндра

Решение Из уравнения конуса
имеем

Областью
интегрирования D является круг,
ограниченный окружностью

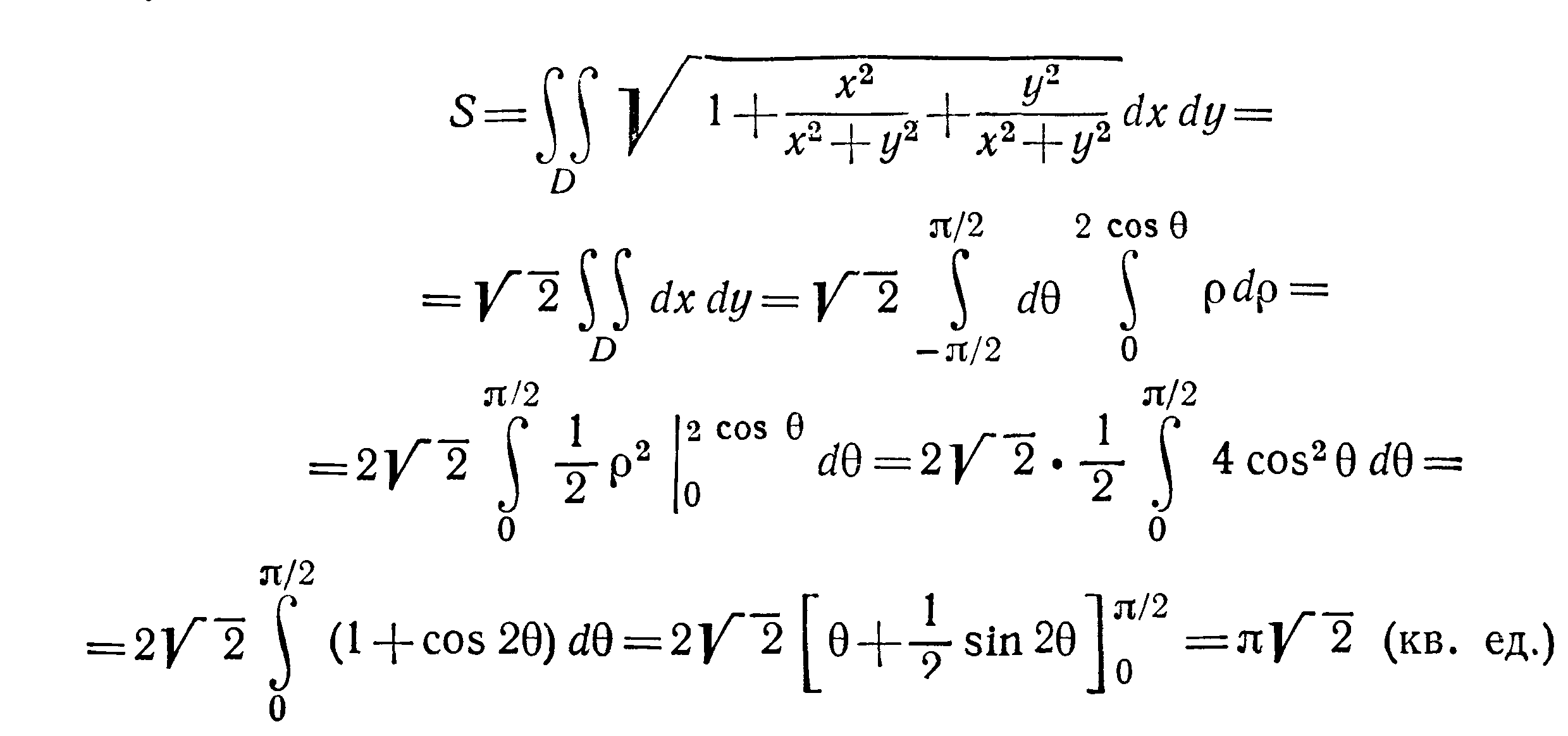
Вычислить площадь поверхности цилиндра

отсеченной плоскостями

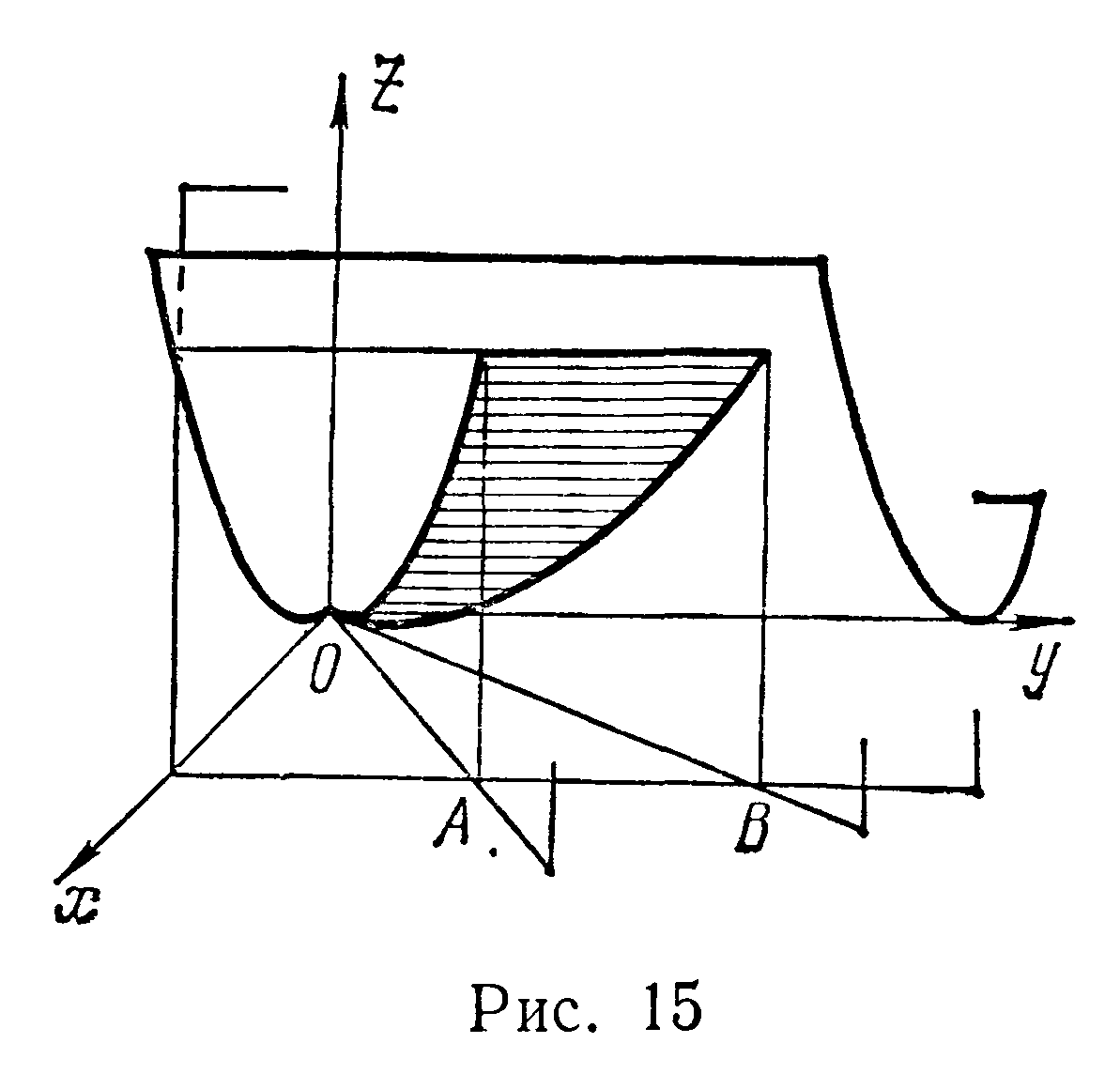
Решение Областью интегрирования
служит треугольник ОАВ. Из уравнения
цилиндра имеем

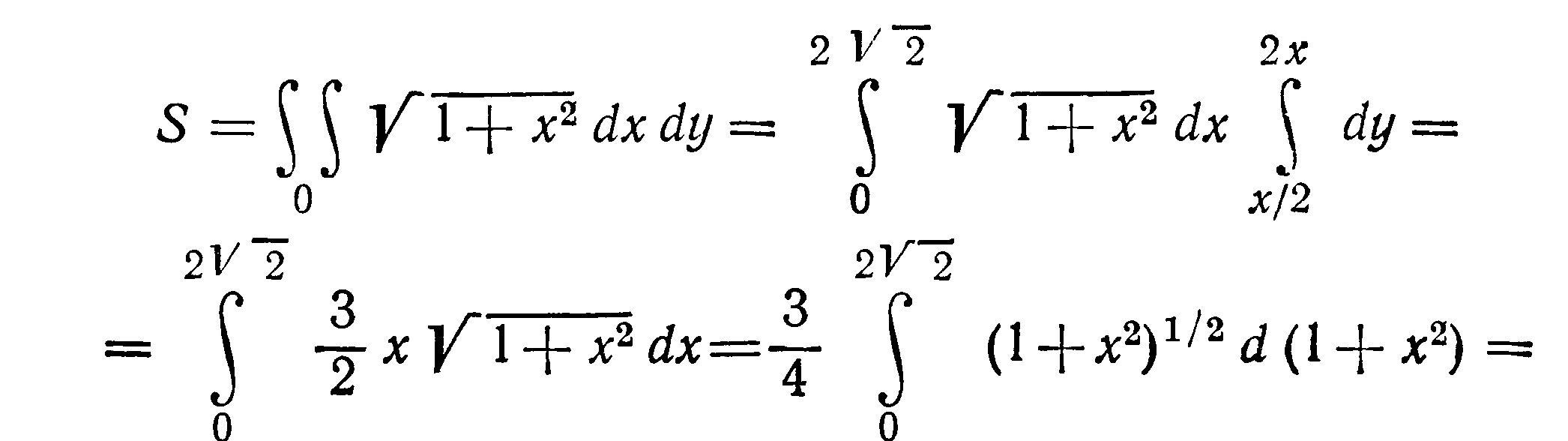
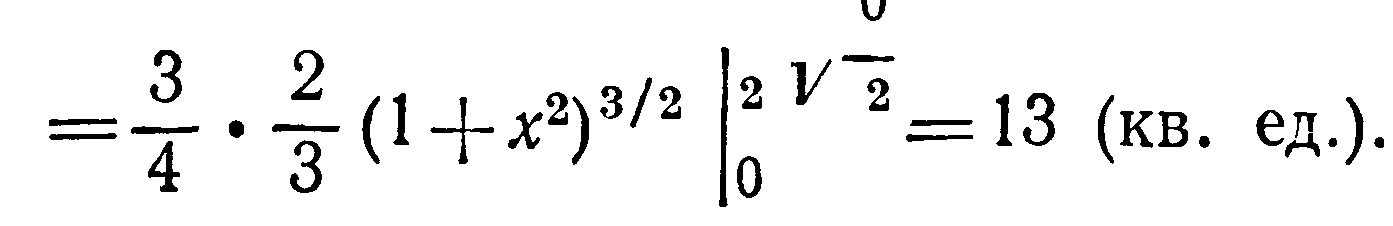
Вычислить площадь части поверхности
параболоида x

,
вырезанной цилиндром

Решение Область интегрирования
— окружность

(она расположена в плоскости yOz).
Из уравнения параболоида имеем

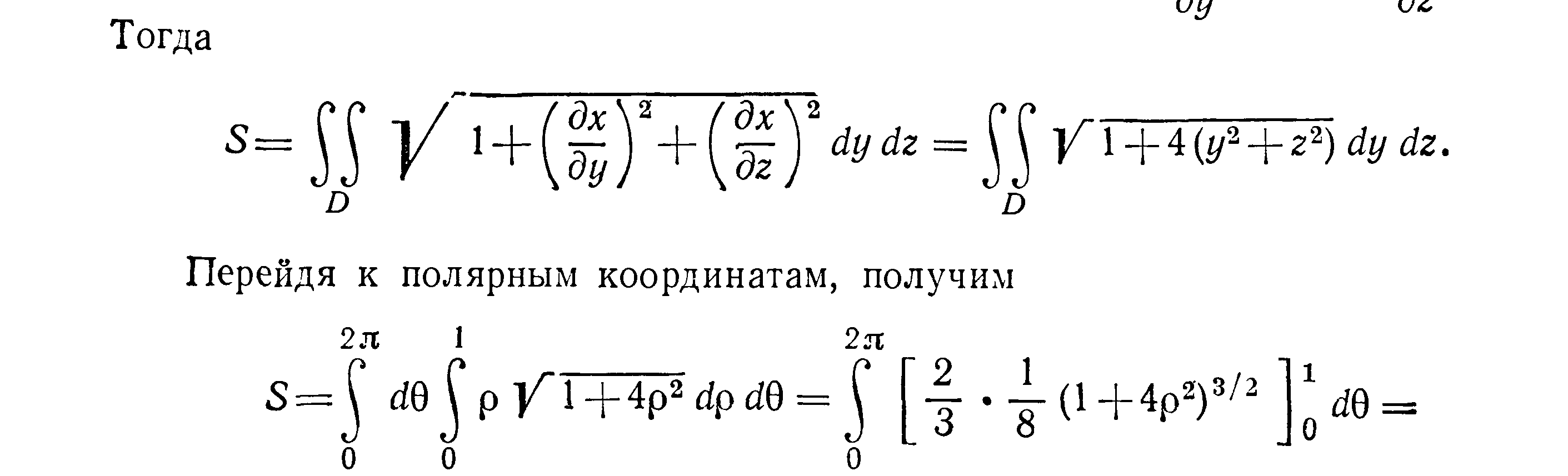
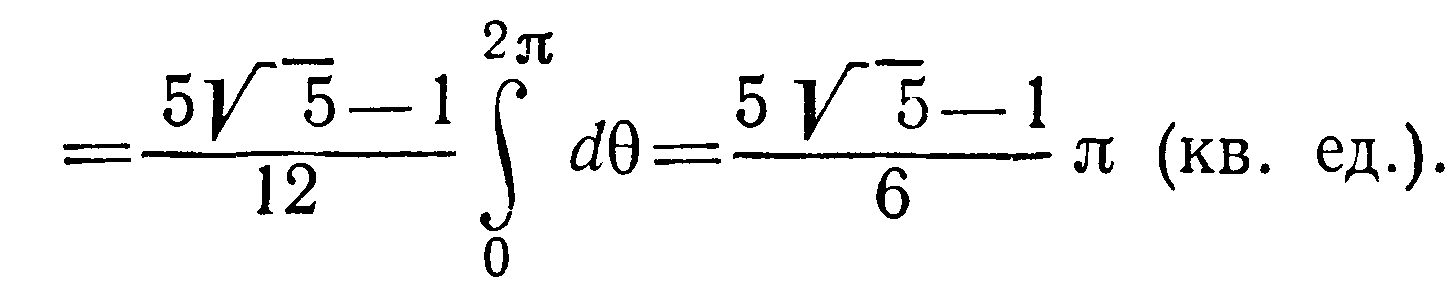
Задачи

36 . Найти площадь части поверхности

вырезанной цилиндром

37. Найти площадь части сферы

вырезанной цилиндром

38. Найти площадь той части плоскости z=
x:, которая заключена
внутри цилиндра

39. Найти площадь части поверхности
цилиндра z = x²,
вырезанной плоскостями

40. Вычислить площадь поверхности конуса

расположенной внутри цилиндра

41. Вычислить площадь поверхности цилиндра

расположенной внутри цилиндра

42. Найти площадь части поверхности

вырезанной плоскостями

Индивидуальные задания

Тройной интеграл

Пусть функция f (х, у, z)
определена в ограниченной замкнутой
пространственной области Т. Разобьем
область Т произвольным образом на п
элементарных областей T₁
Т₂, …, Т_n с
диаметрами d₁ d₂,
…, dn и объемами ∆V₁,
∆V_{2, ….,}∆Vn.
В каждой элементарной области возьмем
произвольную точку P_k
(ξ₁, ξ₂, … , ξ_n
) и умножим значение функции в точке Р_k
на объем этой области.

Интегральной суммой для функции f
(х, у, z) по области Т
называется сумма вида

Предел интегральной суммы при стремлении
к нулю наибольшего из диаметров всех
элементарных областей ∆Vk
называется тройным интегралом от функции
f (х, у, z) по
области Т и обозначается следующим
образом:

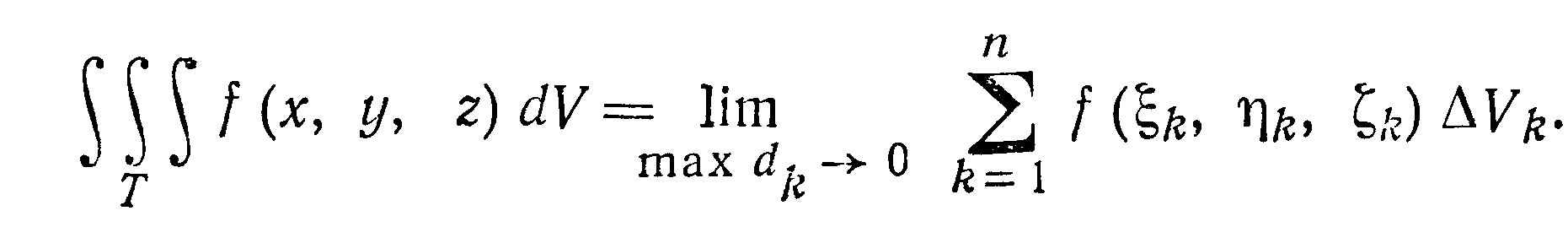
Конечный предел такого вида может
существовать только для ограниченной

функции.

Если f (х, у, z)
> 0 в области Т, то тройной интеграл

представляет собой массу тела, занимающего
область Т и имеющего переменную плотность
γ = f(x, у, z)
(физическое истолкование тройного
интеграла).

Основные свойства тройных интегралов
аналогичны свойствам двойных интегралов.

В декартовых координатах тройной
интеграл обычно записывают в виде

Пусть область интегрирования Т
определяется неравенствами x₁≤
x≤ x_2,y₁≤
y ≤ y_2,z₁≤ z
≤ z_2, гдеy₁(x),
y₂(x),
z₁(x,y),
z₂ (x,y)
непрерывные функции. Тогда тройной
интеграл от функции f (х,
у, z), распространенный на область Т,
вычисляется по формуле

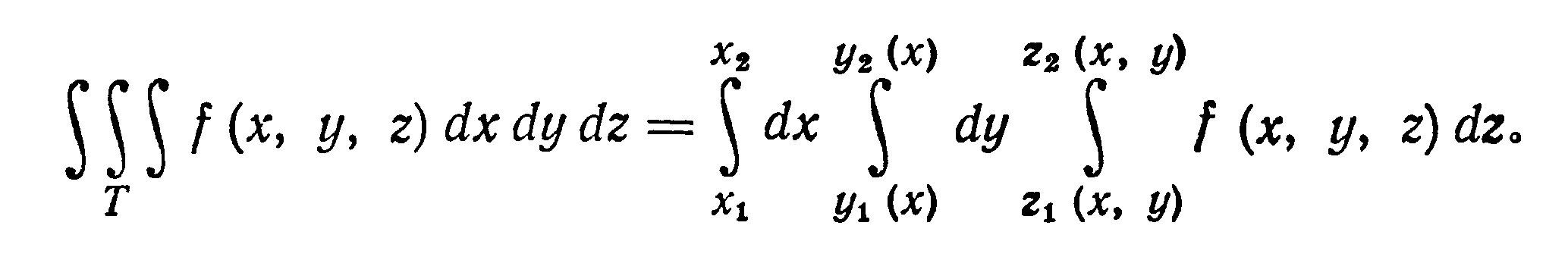
Если при вычислении тройного интеграла
требуется перейти от переменных х, у, z
к новым переменным и, v, w, связанным с х,
у, z соотношениями х = х(u,
v, w), y = y(u, v, w), z = z (u, v, w), где
функции х(и, v, w), y(u,v, w) z (u, v, w), непрерывные
вместе со своими частными производными
первого порядка, устанавливают взаимно
однозначное и в обе стороны непрерывное
соответствие между точками области Т
пространства Oxyz и точками некоторой
области Т’ пространства Ouvw и якобиан J
в области Т’ не обращается в нуль

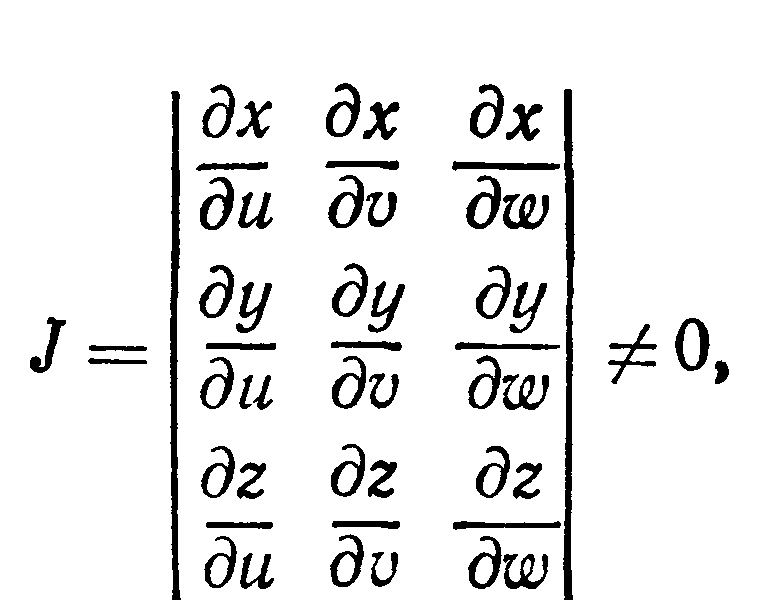
то пользуются формулой

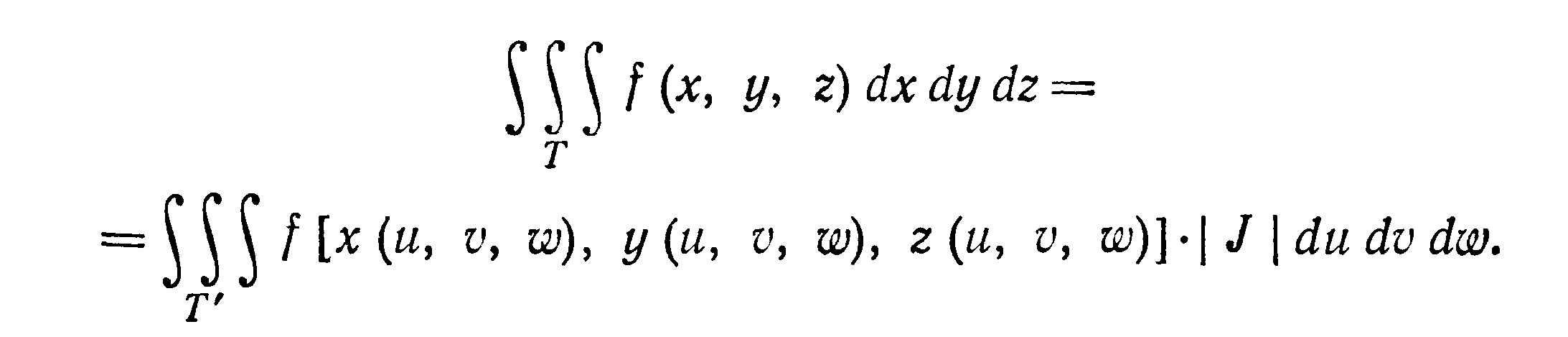
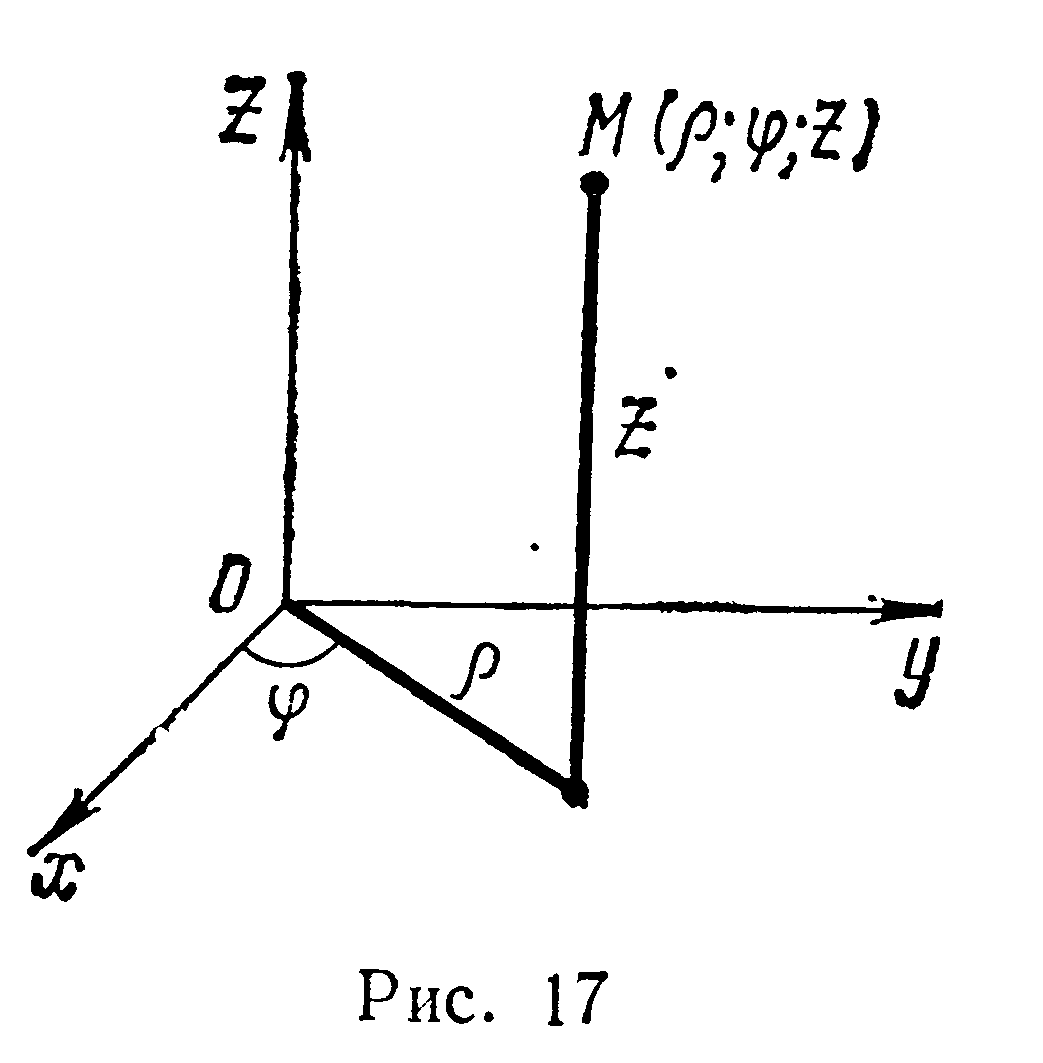
В частности, при переходе от декартовых
координат х, у, z к
цилиндрическим координатам ρ,φ , z
(рис. 17), связанным с х, у, z
соотношениями

якобиан преобразования J = ρ
и формула преобразования тройного
интеграла

к цилиндрическим координатам имеет вид

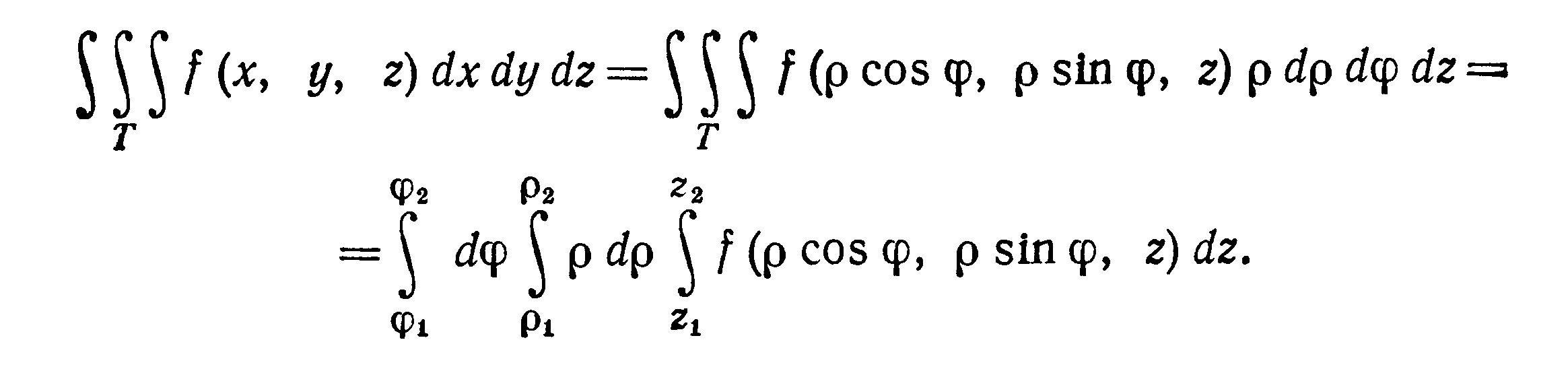
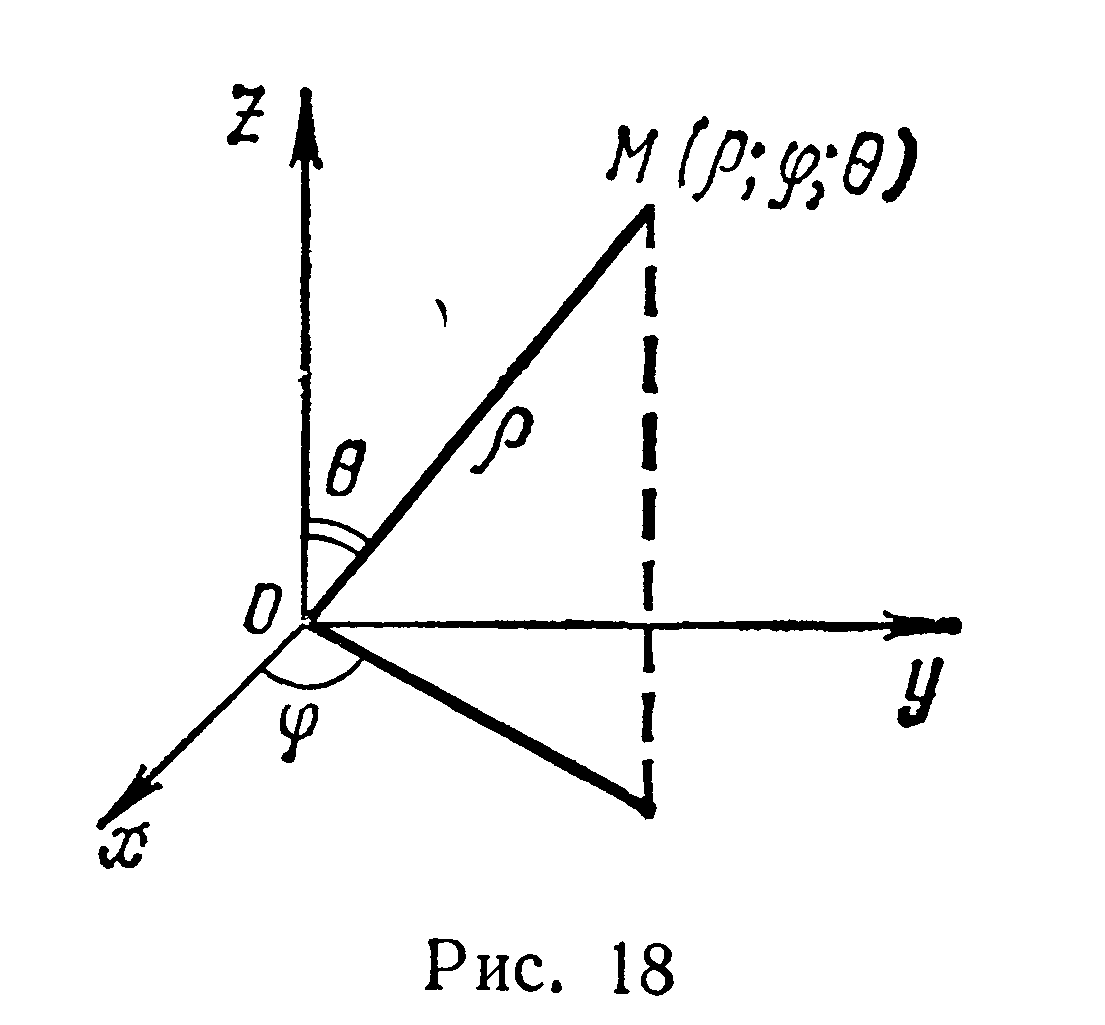
При переходе от декартовых координат
х, у, z к сферическим координатам ρ,φ,θ
(рис. 18), связанным с х, у, z соотношениями

якобиан преобразования J
= ρ² sinθ, и формула
преобразования тройного интеграла к
сферическим координатам имеет вид

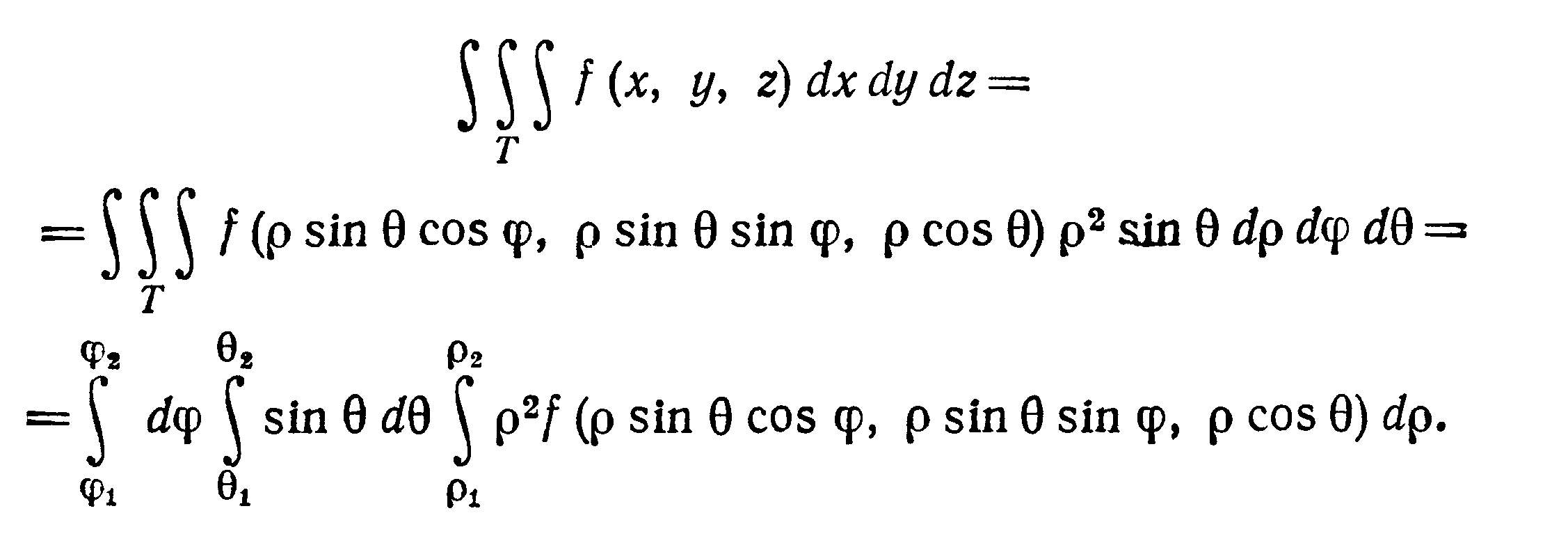
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Общая площадь поверхности параболоида Калькулятор

Search
Дом	математика ↺
математика	Геометрия ↺
Геометрия	3D геометрия ↺
3D геометрия	Параболоид ↺
Параболоид	Площадь поверхности параболоида ↺
Площадь поверхности параболоида	Общая площадь поверхности параболоида ↺

✖Площадь боковой поверхности параболоида — это общее количество двухмерных плоскостей, заключенных на боковой криволинейной поверхности параболоида.ⓘ Площадь боковой поверхности параболоида [LSA]

+10%

-10%

✖Радиус параболоида определяется как длина прямой линии от центра до любой точки на окружности круглой грани параболоида.ⓘ Радиус параболоида [r]

+10%

-10%

✖Общая площадь поверхности параболоида – это общее количество двухмерного пространства, заключенного на всей поверхности параболоида.ⓘ Общая площадь поверхности параболоида [TSA]

⎘ копия

Общая площадь поверхности параболоида Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Площадь боковой поверхности параболоида: 530 Квадратный метр —> 530 Квадратный метр Конверсия не требуется
Радиус параболоида: 5 метр —> 5 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

608.539816339745 Квадратный метр —> Конверсия не требуется

1 Общая площадь поверхности параболоида Калькуляторы

Общая площадь поверхности параболоида формула

Общая площадь поверхности параболоида = Площадь боковой поверхности параболоида+(pi*Радиус параболоида^2)

TSA = LSA+(pi*r^2)

Что такое параболоид?

В геометрии параболоид — это квадратичная поверхность, имеющая ровно одну ось симметрии и не имеющая центра симметрии. Термин «параболоид» происходит от параболы, которая относится к коническому сечению, обладающему аналогичным свойством симметрии. Всякое плоское сечение параболоида плоскостью, параллельной оси симметрии, есть парабола. Параболоид является гиперболическим, если каждое второе сечение плоскости является либо гиперболой, либо двумя пересекающимися прямыми (в случае сечения касательной плоскостью). Параболоид эллиптический, если каждое другое непустое плоское сечение является либо эллипсом, либо одной точкой (в случае сечения касательной плоскостью). Параболоид бывает либо эллиптическим, либо гиперболическим.

Источник

Площадь поверхности вращения тела

Пусть даны прямая и кривая Gamma , лежащая в одной плоскости с и расположенная по одну сторону от этой прямой. При вращении кривой Gamma вокруг оси получается поверхность lambda , площадь которой мы и хотим сначала определить, а потом вычислить (см. 46).

Начнем со случая, когда Gamma — отрезок, один конец которого отстоит от на , а другой — на (рис. 58). Тогда, как доказывается в школьном курсе геометрии, площадь поверхности вращения (боковой поверхности усеченного конуса) выражается формулой P(lambda)=pi(r+R)ell . В этом случае при r leqslant R имеем:

Прямая и кривая, лежащая в одной плоскости с прямой

2picdot rcdot ell leqslant P(lambda) leqslant 2picdot Rcdot ell,.

(1)

Таким образом, боковая поверхность конуса заключена между произведением длины образующей на длину наименьшей окружности и произведением длины образующей на длину наибольшей окружности.

То же самое неравенство будет иметь место и при вращении любой ломаной линии, расположенной по одну сторону от оси вращения:

2picdot rcdot ell leqslant P(lambda) leqslant 2picdot Rcdot ell,.

(2)

где и — наименьшее и наибольшее расстояния точек ломаной от оси , и ell — длина ломаной.

Для доказательства достаточно применить неравенство (1) к каждому звену ломаной, сложить полученные результаты и учесть что Sigmaell_k=ell и для любого звена имеем r leqslant r_k и R_k leqslant R (здесь r_k и R_k — наименьшее и наибольшее расстояния точек k-ro звена от оси вращения).

Естественно потребовать, чтобы неравенства (2) выполнялись для любой спрямляемой кривой. Кроме того, потребуем, чтобы площадь поверхности вращения обладала свойством аддитивности: при разбиении дуги Gamma на части $gamma_0, gamma_1, ldots, gamma_{n-1}$ должно выполняться равенство

$P(lambda)= sum_{k=0}^{n-1} P(omega_k),$

(3)

где lambda — поверхность, полученная при вращении всей дуги Gamma , а omega_k — при вращении части gamma_k .

Если применить к каждой части omega_k неравенства (2), то получим, что

2picdot r_kcdot ell_k leqslant P(omega_k) leqslant 2picdot R_kcdot ell_k,,

где ell_k=ell(gamma_k) — длина дуги gamma_k , а r_k и R_k — наименьшее и наибольшее расстояния точек этой дуги gamma_k от оси вращения. Складывая эти неравенства и учитывая требование аддитивности, получаем, что

$2pi sum_{k=0}^{n-1} r_kell_k leqslant P(lambda) leqslant 2pi sum_{k=0}^{n-1} R_kell_k,.$

(4)

Иными словами, площадь поверхности вращения должна разделять множества

$Biggl{~2pi sum_{k=0}^{n-1} r_kell_k~Biggr},qquad Biggl{~2pi sum_{k=0}^{n-1} R_kell_k~Biggr}.$

Именно это требование мы и примем за определение площади поверхности вращения.

Если Gamma — плоская спрямляемая кривая, лежащая по одну сторону от оси , то площадью поверхности lambda , получаемой при вращении этой кривой вокруг оси , называется число P(lambda) , разделяющее множества

$Biggl{~2pi sum_{k=0}^{n-1} r_kell_k~Biggr},qquad Biggl{~2pi sum_{k=0}^{n-1} R_kell_k~Biggr},$

соответствующие всевозможным разбиениям дуги Gamma . Здесь r_k,,R_k и ell_k имеют указанный выше смысл.

Докажем сейчас, что это число существует и единственно, а затем выведем для него выражение в виде интеграла. Выберем на плоскости систему координат, такую, что ось абсцисс совпадает с осью вращения. Зададим параметризацию кривой Gamma , выбрав в качестве параметра длину ell дуги , соединяющей в заданном направлении фиксированную точку кривой Gamma с произвольной точкой этой кривой (рис. 59). Тогда r_k и R_k будут наименьшими и наибольшими значениями ординаты для точек части gamma_k .

Произвольная точка на кривой

Поэтому суммы, стоящие в неравенствах (4) слева и справа, являются не чем иным, как суммами Дарбу для интеграла $2piintlimits_{0}^{L} y(ell),dell$ , где через обозначена длина всей кривой Gamma . Поскольку функция y(ell) непрерывна в силу непрерывности кривой Gamma , то существование и единственность числа, разделяющего эти суммы Дарбу, вытекают из теоремы существования интеграла от непрерывной функции. При этом мы доказали, что площадь поверхности вращения, т. е. число P(lambda) , разделяющее эти суммы, равняется интегралу:

$P(lambda)= 2piintlimits_{0}^{L} y(ell),dell,.$

(5)

Из формулы (5) получаются различные частные случаи в зависимости от того, как задана кривая Gamma . Если она задана параметрически:

$begin{cases}x=varphi(t),\ y=psi(t),end{cases} t_0 leqslant t leqslant T$ , то $dell= sqrt{bigl(varphi'(t)bigr)^2+ bigl(psi'(t)bigr)^2},dt$ ,

и формула (5) принимает вид:

$P(lambda)= 2pi intlimits_{t_0}^{T} psi(t) sqrt{bigl(varphi'(t)bigr)^2+ bigl(psi'(t)bigr)^2},dt$

(6)

(когда ell меняется от до , переменная { t} меняется от ${ t_0}$ до ).

В частности, если кривая Gamma задана явным уравнением y=f(x),~ a leqslant x leqslant b , то

$P(lambda)= 2pi intlimits_{a}^{b} f(x) sqrt{1+bigl(f'(x)bigr)^2},dx= 2pi intlimits_{a}^{b}ysqrt{1+(y')^2},dx,.$

(7)

Если кривая Gamma задана в полярных координатах уравнением rho=f(varphi) , где alpha leqslant varphi leqslant beta , а функция имеет непрерывную производную f'(varphi) на [alpha;beta] , то, учитывая, что y= rhosinvarphi= f(varphi)sinvarphi , a $dell= sqrt{rho_{varphi}^{prime2}+ rho^2},dvarphi$ , получим:

$P=2pi intlimits_{alpha}^{beta} rhosinvarphi sqrt{rho_{varphi}^{prime2}+ rho^2},dvarphi,.$

(8)

Пример 1. Найдем площадь поверхности шара радиуса .

Решение. Поместим начало координат в центр шара. Будем рассматривать поверхность шара как поверхность, полученную в результате вращения полуокружности x^2+y^2=R^2 вокруг оси . Тогда площадь поверхности шара найдется по формуле

$P=2pi intlimits_{-R}^{R} ysqrt{1+(y')^2},dx,.$

Так как $y=sqrt{R^2-x^2}$ — функция четная, то

$P=4pi intlimits_{0}^{R} ysqrt{1+(y')^2},dx,.$

Найдя $y'= frac{-x}{sqrt{R^2-x^2}}$ и вычислив сумму $1+(y')^2= 1+frac{x^2}{R^2-x^2}= frac{R^2}{R^2-x^2}$ , получим:

$P= 4pi intlimits_{0}^{R}! sqrt{R^2-x^2}cdot frac{R,dx}{sqrt{R^2-x^2}}= 4pi Rintlimits_{0}^{R}dx= Bigl.{4pi Rx}Bigr|_{0}^{R}= 4pi nR^2.$

Пример 2. Вычислить площадь поверхности, образованной вращением одной арки циклоиды вокруг Ox:

$begin{cases}x=a(t-sin{t}),\ y=a(1-cos{t}),end{cases} 0 leqslant t leqslant 2pi,.$

Решение. Найдем $x'_t=a(1-cos{t}),~ y'_t=asin{t}$ . Тогда

$(x'_t)^2+(y'_t)^2= 2a^2(1-cos{t})= 4a^2sin^2frac{t}{2},.$

Искомая площадь поверхности вращения равна

$begin{aligned}P&= 2pi intlimits_{0}^{2pi} a(1-cos{t})2asin frac{t}{2},dt= 8pi a^2 intlimits_{0}^{2pi}sin^3 frac{t}{3},dt= 8pi a^2 intlimits_{0}^{2pi}! left(1-cos^2 frac{t}{2} right)! sin frac{t}{2},dt=\ &= left.{8pi a^2! left(-2cos frac{t}{2}+ frac{2}{3}cos^3 frac{t}{2}right)}right|_{0}^{2pi}= frac{64}{3},pi a^2.end{aligned}$

Пример 3. Найдем площадь поверхности, образованной вращением лемнискаты rho^2=a^2cos2varphi вокруг полярной оси.

Решение. Имеем: $rho= asqrt{cos2varphi}~ Rightarrow~ rho'_{varphi}= frac{-asin2varphi}{sqrt{cos2varphi}}$ . Поэтому

$rho^{2}+rho_{varphi}^{prime2}= a^2cos2varphi+ frac{a^{2} sin^{2}2varphi}{cos2varphi}= a^2! left(cos2varphi+ frac{sin^{2}2varphi}{cos2varphi}right)= frac{a^{2}}{cos2varphi},.$

Пользуясь формулой (8) для вычисления площади поверхности в полярных координатах, найдем сначала половину искомой площади поверхности:

$frac{1}{2}P= 2pi intlimits_{0}^{pi/4} asqrt{cos2varphi}, frac{sinvarphicdot a}{sqrt{cos2varphi}}, dvarphi= 2pi a^2 intlimits_{0}^{pi/4} sinvarphi,dvarphi= 2pi a^2cdot frac{2-sqrt{2}}{2}= pi a^2bigl(2-sqrt{2}bigr).$

Вся площадь данной поверхности будет равна $P=2bigl(2-sqrt{2}bigr)pi a^2$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник