Как найти площадь поверхности параллелепипеда через объем

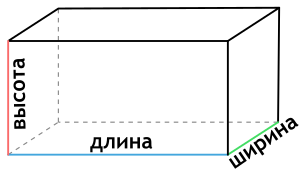
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.

Свойства прямоугольного параллелепипеда:

1. В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
2. Противоположные грани попарно равны и параллельны.
3. Все двугранные углы прямоугольного параллелепипеда – прямые.
4. Диагонали прямоугольного параллелепипеда равны.
5. Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

$B_1D^2=AD^2+DC^2+C_1C^2$

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

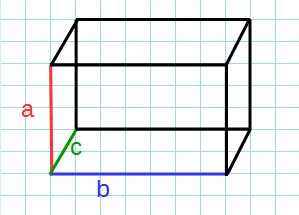
Чтобы были понятны формулы, введем обозначения:

$а$ — длина;

$b$ — ширина;

$с$ — высота(она же боковое ребро);

$P_{осн}$ — периметр основания;

$S_{осн}$ — площадь основания;

$S_{бок}$ — площадь боковой поверхности;

$S_{п.п}$ — площадь полной поверхности;

$V$ — объем.

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

$S_{бок}=P_{осн}·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.

$S_{п.п}=2(ab+bc+ac).$

Дополнительные сведения, которые пригодятся для решения задач:

Куб

$а$ — длина стороны.

$V=a^3;$

$S_{бок}=4а^2;$

$S_{п.п}=6а^2;$

$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Объем любой пирамиды равен трети произведения основания и высоты.

$V={1}/{3}S_{осн}·h$

В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

Площадь треугольника.

• $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$.
• $S={a·b·sin⁡α}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
• Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$.
• $S=p·r$, где $r$ — радиус вписанной окружности.
• $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности.
• Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
• Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ — длина стороны. 

В основании лежит четырехугольник.

1. Прямоугольник.
   $S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб.
   $S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба.
   $S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
3. Трапеция.
   $S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
4. Квадрат.
   $S=a^2$, где $а$ — сторона квадрата.

Теорема Пифагора.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Стоит использовать формулы, которые есть для данной фигуры.

Согласно правилам, для определения площади параллелепипеда надо знать его стороны.

S = 2(ab + ac + bc).

Однако, в самом примере мы знаем только два стороны из трех. Но нам известен и объем фигуры, который вычисляется формуле.

V = abc.

V = 112 см3, a=2, b=7.

с = V/ab = 112/2*7 = 112/14 = 8.

Теперь можно высчитать площадь:

S = 2(2*7 + 2*8 + 7*8) = 2(14 + 16 + 56) = 2 * 86 = 172 см2.

При желании можно было бы написать написать одну формулу, соединив все, без отдельного вычисления третьей стороны. Но так она была бы слишком большой и легко можно было бы допустить ошибку.

Как найти площадь поверхности параллелепипеда

На данной странице калькулятор поможет рассчитать площадь поверхности параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину.

Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.