Wafer Dirt
[263]
3 года назад
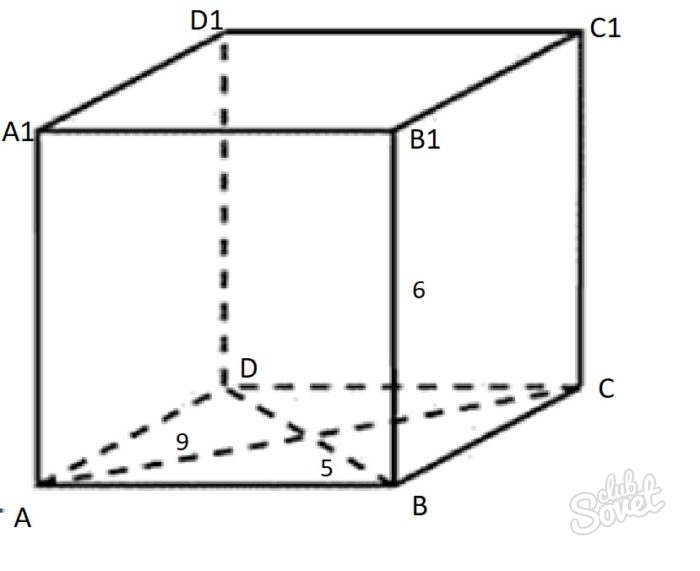
1) Диагональ, известная сторона (с) и диагональ нижнего основания образуют прямоугольный тр-ник. Нижнюю диагональ находим по т-ме Пифагора: √(6^2 — 4^2)= √(36-16) = √20;
2) Нижняя диагональ и другая известная сторона (в) образуют другой прямоугольный тр-ник. По той же т-ме Пифагора найдём сторону а: а = √((√20)^2 — 2^2) = √(20-4) = √16 = 4
3) Находим площадь поверхности параллелепипеда по формуле S = (aв + вс + ас)•2 = (4•2 + 2•4 + 4•4)•2 = 64
Ответ: 64
Прикрепляю фотографию, чтоб было понятнее
автор вопроса выбрал этот ответ лучшим
комментировать
в избранное
ссылка
отблагодарить
Как найти площадь поверхности параллелепипеда
Призма, у которой все стороны являются параллелограммами, и есть параллелепипед. Коробка, холодильник, здания, аквариум, кусочек сахара-рафинада – вот немногие примеры параллелепипеда в нашей повседневной жизни.
1
Разновидность, свойства параллелепипеда
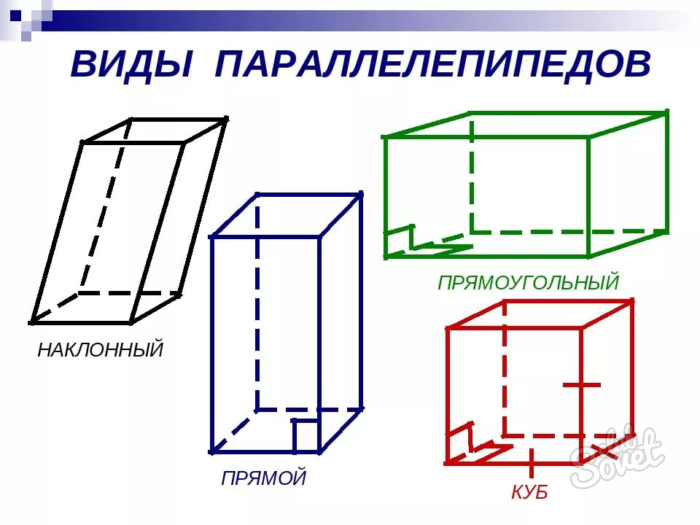
Различают прямой и наклонный параллелепипед.
Прямой – это тот, ребра которого перпендикулярны основанию плоскости. Если основанием является прямоугольник, тогда фигура называется прямоугольным параллелепипедом. Если основанием и боковыми гранями является квадрат – куб.
Наклонный параллелепипед имеет наклон боковых граней к основанию под углом, отличным от 90 градусов.
Свойства параллелепипеда:
- Противоположные грани равны и параллельны.
- Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов 3-х его измерений, т.е. D^2=a^2+b^2+c^2.
- Все диагонали пересекаются в одной точке, делящей их пополам.
- Параллелепипед симметричен по отношению к середине его диагонали.
2
Площадь поверхности параллелепипеда
Как известно, существует несколько разновидностей параллелепипеда, поэтому и формулы для нахождения площади полной поверхности будут различаться.
Прямоугольный параллелепипед
У прямоугольного параллелепипеда основания и боковые грани – прямоугольники.
В данном случае используется формула S(п)=2(a*b+b*c+a*c).
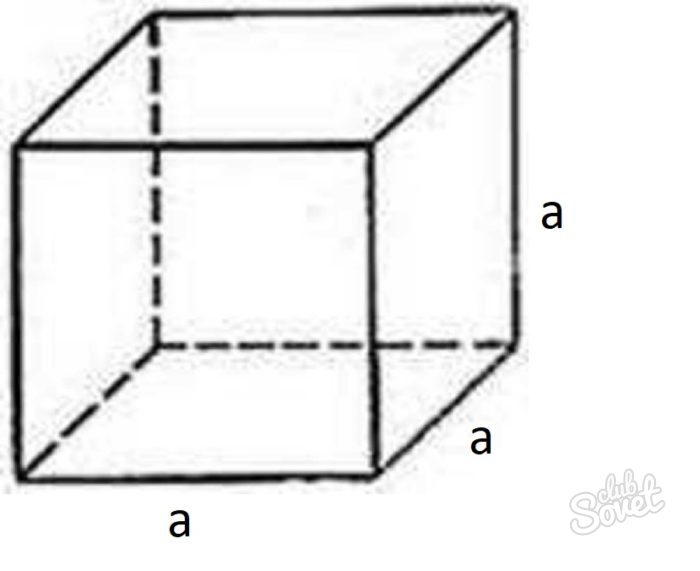
Куб
Куб является частным случаем параллелепипеда. У него все стороны равны. Воспользовавшись формулой выше, получаем S(п)=2(a*a+a*a+a*a). В результате преобразования можно получить сокращенную версию формулы для нахождения площади полной поверхности куба S(п)=6*a^2.
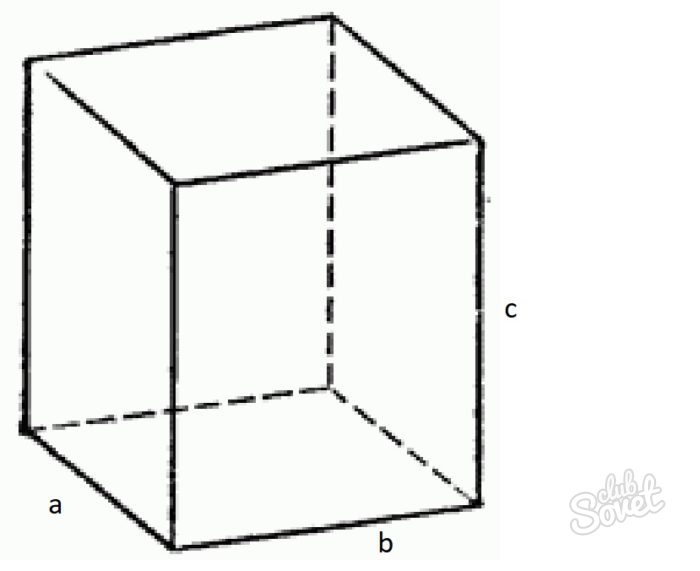
Прямой параллелепипед
В то время, когда у прямоугольного параллелепипеда основанием является прямоугольник, прямой может иметь там любой параллелограмм, будь то квадрат или ромб. Именно поэтому формула для нахождения площади полной поверхности такой фигуры будет иной: S(п)=S(б)+2S(о), где S(о) – площадь основания, S(б) – площадь боковой поверхности.
Площадь основания S(о) будет зависеть от того, какая фигура лежит в основании.
В свою очередь, площадь боковой поверхности рассчитывается, как S(б)=P(о)*h, где P(о) – периметр основания, h – высота.
3
Как найти площадь поверхности параллелепипеда – пример
Основанием прямого параллелепипеда служит ромб. Меньшая его диагональ равна 5 см, большая диагональ – 9 см, периметр равен 20 см. Найти площадь полной поверхности параллелепипеда, если его высота равна 6 см.
Для решения задачи понадобится формула S(п)=S(б)+2S(о).
В основании параллелепипеда лежит ромб, следовательно, его площадь необходимо найти.
S(б)=P(о)*h=20*6=120 см^2
S(о)=(d1+d2)/2=(5+9)/2=7см^2
Подставив данные в формулу, получаем S(п)=120+2*7=134 см^2.
Человека окружает множество вещей-параллелепипедов. Системный блок компьютера, кирпич, шкаф, различные архитектурные сооружения. Даже не замечая, параллелепипед занял значимое место в современном мире.
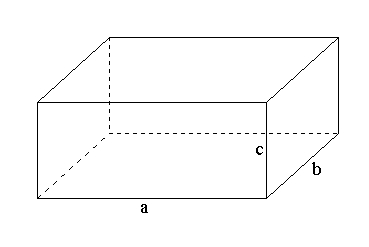
Параллелепипед – это многогранник с 6 гранями, каждая из которых является параллелограммом.
Прямоугольный параллелепипед – это параллелепипед, каждая грань которого является прямоугольником.
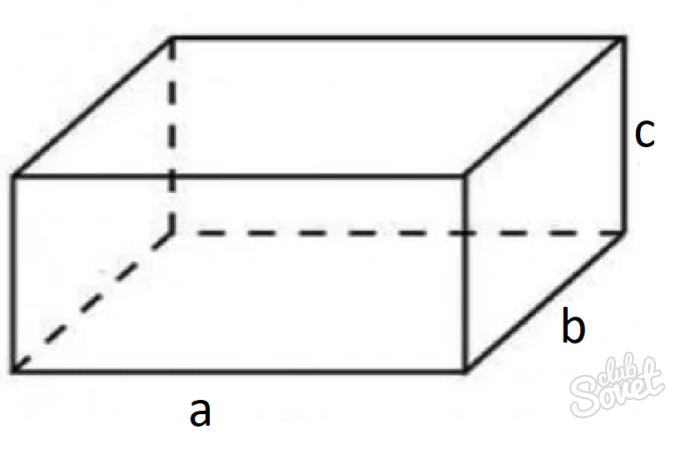
Любой параллелепипед характеризуется 3 сторонами a, b и c (см. рисунок) и диагональю. Именно эти характеристики используются в формулах параллелепипеда при вычислении объема и площади.
Диагональ параллелепипеда – это отрезок, соединяющий противоположные вершины параллелепипеда.
Формула диагонали параллелепипеда
Диагональ d прямоугольного параллелепипеда можно получить, зная его стороны:
d2 = a2 + b2 + c2
Формула площади параллелепипеда
Площадь поверхности прямоугольного параллелепипеда можно получить, зная его стороны:
S = 2(ab + ac + bc)
Формула объема параллелепипеда
Объем прямоугольного параллелепипеда можно вычислить, зная его стороны:
V = abc
Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Определение.
Прямоугольный параллелепипед — это многогранная объемная фигура ограничена шестью прямоугольниками.
Куб является частным случаем прямоугольного параллелепипеда.
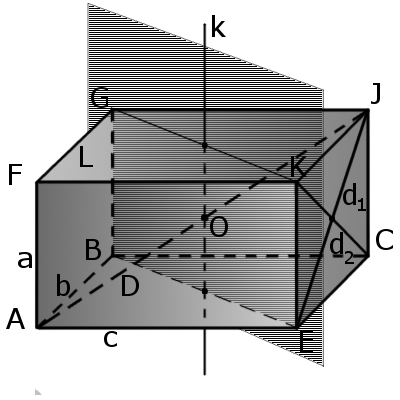 |
|
| Рис.1 |
Основные свойства правильного прямоугольного параллелепипеда
Противоположные грани прямоугольного параллелепипеда параллельны и равны.
Ребра прямоугольного параллелепипеда, которые сходятся в одной вершине взаимно перпендикулярны.
Не параллельные грани прямоугольного параллелепипеда пересекаются под прямым углом.
У прямоугольного параллелепипеда четыре диагонали.
Диагонали прямоугольного параллелепипеда равны между собой и пересекаются в одной точке.
Объем прямоугольного параллелепипеда
Формула. Объем прямоугольного параллелепипеда равна произведению длин его сторон:
V = a · b · c
Площадь поверхности прямоугольного параллелепипеда
Определение. Поверхность прямоугольного параллелепипеда состоит из суммы площадей прямоугольников, ограничивающие его.
Формула. Площадь поверхности прямоугольного параллелепипеда через длины его сторон:
S = 2a·b + 2a·c + 2b·c
Диагональ прямоугольного параллелепипеда
Определение. Диагональ прямоугольного параллелепипеда — это отрезок, соединяющий две не соседние вершины, лежащие на разных гранях.
Формула. Длина диагонали прямоугольного параллелепипеда через длины его сторон:
d = √a2 + b2 + c2
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.
Свойства прямоугольного параллелепипеда:
- В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
- Противоположные грани попарно равны и параллельны.
- Все двугранные углы прямоугольного параллелепипеда – прямые.
- Диагонали прямоугольного параллелепипеда равны.
- Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
$B_1D^2=AD^2+DC^2+C_1C^2$
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$а$ — длина;
$b$ — ширина;
$с$ — высота(она же боковое ребро);
$P_{осн}$ — периметр основания;
$S_{осн}$ — площадь основания;
$S_{бок}$ — площадь боковой поверхности;
$S_{п.п}$ — площадь полной поверхности;
$V$ — объем.
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_{бок}=P_{осн}·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
$S_{п.п}=2(ab+bc+ac).$
Дополнительные сведения, которые пригодятся для решения задач:
Куб
$а$ — длина стороны.
$V=a^3;$
$S_{бок}=4а^2;$
$S_{п.п}=6а^2;$
$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Объем любой пирамиды равен трети произведения основания и высоты.
$V={1}/{3}S_{осн}·h$
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
Площадь треугольника.
- $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$.
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$.
- $S=p·r$, где $r$ — радиус вписанной окружности.
- $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности.
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
- Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ — длина стороны.
В основании лежит четырехугольник.
- Прямоугольник.
$S=a·b$, где $а$ и $b$ — смежные стороны. - Ромб.
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба.
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами. - Трапеция.
$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции. - Квадрат.
$S=a^2$, где $а$ — сторона квадрата.
Пример:
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.
Решение:
Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.
Объем пирамиды, в основании которой лежит прямоугольник
$V={S_{прямоугольника}·h}/{3}={a·b·h}/{3}$, где $a$ и $b$ — стороны прямоугольника.
Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.
В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.
Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).
$СС_1=АА_1=4$
$V={А_1В_1·A_1D_1·СС_1}/{3}={8·12·4}/{3}=128$
Ответ: $128$
Теорема Пифагора.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$