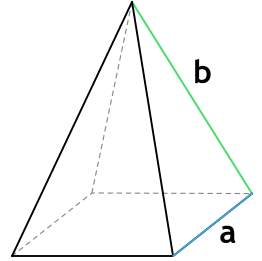
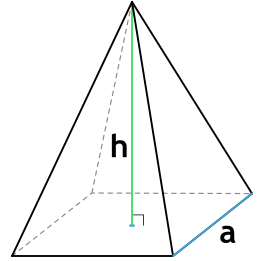
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.
Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.
-
Формула площади правильной пирамиды
- 1. Общая формула
- 2. Площадь правильной треугольной пирамиды
- 3. Площадь правильной четырехугольной пирамиды
- 4. Площадь правильной шестиугольной пирамиды
Формула площади правильной пирамиды
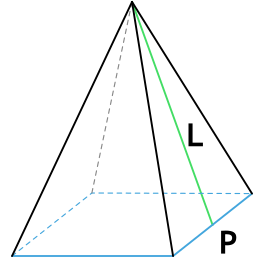
1. Общая формула
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.
Sполн. = Sбок. + Sосн.
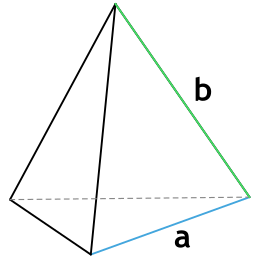
Боковой гранью правильной пирамиды является равнобедренный треугольник.
Площадь треугольника вычисляется по формулам:
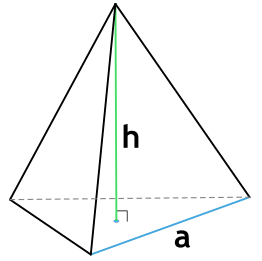
1. Через длину основания (a) и высоту (h):
2. Через основание (a) и боковую сторону (b):
Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.
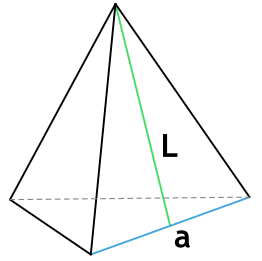
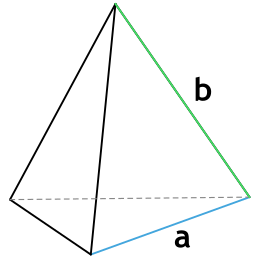
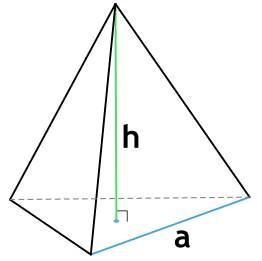
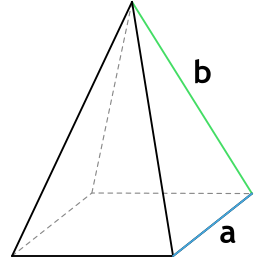
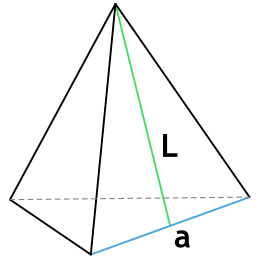
2. Площадь правильной треугольной пирамиды
Основание: равносторонний треугольник.
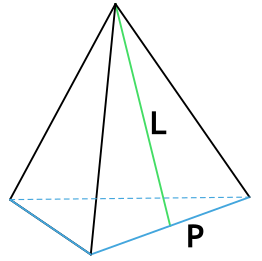
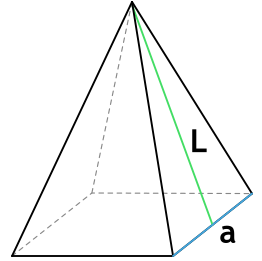
L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.
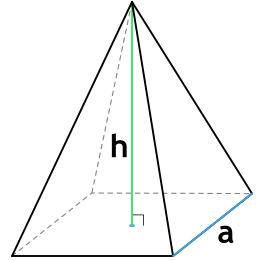
3. Площадь правильной четырехугольной пирамиды
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 2aL |
 |
|
| полная | Sполн. = a2 + 2aL |
 |
microexcel.ru
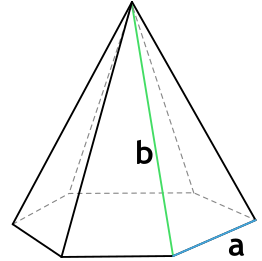
4. Площадь правильной шестиугольной пирамиды
Основание: правильный шестиугольник

{S_{полн} = dfrac{1}{2}PL + S}
На странице вы найдете онлайн-калькуляторы, которые помогут найти площадь полной и боковой поверхности правильной пирамиды, а также треугольной, четырехугольной и шестиугольной пирамиды. Кроме того приводятся формулы, по которым вы можете произвести расчет самостоятельно.
- калькулятор площади поверхности пирамиды
- формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
- формула площади полной поверхности правильной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и боковую грань
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной пирамиды через периметр и апофему
- формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- примеры задач
Познакомьтесь с важными понятиями, которые необходимо знать для расчета площади поверхности пирамиды.
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.
Площадь полной поверхности пирамиды — это сумма площадей боковых граней и площади основания.
Площадь боковой поверхности пирамиды — это совокупная площадь всех боковых граней пирамиды.
Апофема — перпендикуляр, опущенный из вершины пирамиды на ребро основания.
Формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
{S_{полн} = dfrac{1}{2}PL+S}
P — периметр основания пирамиды
L — апофема пирамиды
S — площадь основания пирамиды
Формула площади полной поверхности правильной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{na}{2} {Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} + sqrt{h^2+ Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
n — число сторон основания
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{a^2 sqrt{3}+6aL}{4}}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{a^2 sqrt{3}+6a sqrt{b^2 — dfrac{a^2}{4}}}{4}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{3a}{2} {Bigg( dfrac{a}{2 tg ( 60°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{полн} = 2a {Bigg( dfrac{a}{2 tg ( 45°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{полн} = a^2+2aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3asqrt{b^2-dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{полн} = 3a {Bigg( dfrac{a}{2 tg ( 30°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной пирамиды через периметр и апофему
{S_{бок} = dfrac{1}{2}PL}
P — периметр основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{na}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( dfrac{180°}{n})} Bigg) ^2} }
a — сторона основания пирамиды
h — высота пирамиды
n — число сторон основания
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{бок} = dfrac{3}{2}aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{бок} = dfrac{3a sqrt{b^2 — dfrac{a^2}{4}}}{2}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{3a}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
{S_{бок} =dfrac{1}{2}PL}
P — периметр основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{бок} = 2aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 2a sqrt{b^2 — dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{бок} = 3aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 3asqrt{b^2-dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{бок} = 3a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Примеры задач на нахождение площади поверхности пирамиды
Задача 1
Стороны основания правильной четырехугольной пирамиды равны 60см, боковые ребра равны 78см. Найдите площадь поверхности этой пирамиды.
Решение
Так как пирамида правильная четырехугольная, то воспользуемся соответствующей формулой площади поверхности через сторону основания и боковую грань.
S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}} = 60^2 + 2 cdot 60 sqrt{78^2- dfrac{60^2}{4}} = 3600 + 120 sqrt{6084- dfrac{3600}{4}} = 3600 + 120 sqrt{6084 — 900} = 3600 + 120 sqrt{5184} = 3600 + 120 cdot 72 = 3600 + 8640 = 12240 : см²
Ответ: 12240 см²
Проверим полученный ответ с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной треугольной пирамиды со стороной 6см и апофемой 10см.
Решение
Из условия мы знаем апофему и сторону правильной треугольной пирамиды, поэтому нам потребуется эта формула.
S_{бок} = dfrac{3}{2}aL = dfrac{3}{2} cdot 6 cdot 10 = dfrac{3}{2} cdot 60 = 90 : см²
Ответ: 90 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной четырехугольной пирамиды сторона основания 6см и высота 4см.
Решение
Подставим значения в формулу и произведем расчет.
S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} = 2 cdot 6 sqrt{4^2+ Bigg( dfrac{6}{2 tg ( 45°)} Bigg) ^2} = 60 : см²
Ответ: 60 см²
Проверка .
Как найти площадь поверхности пирамиды
На данной странице калькулятор поможет рассчитать площадь поверхности пирамиды онлайн. Для расчета задайте площадь основания и апофему.
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.
Апофема – опущенный перпендикуляр из вершины на ребро основания.
Боковая поверхность через периметр и апофему
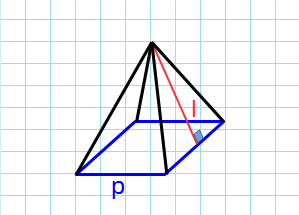
Формула площади боковой поверхности правильной пирамиды через периметр и апофему:
p — периметр основания пирамиды; l — апофема пирамиды.
Боковая поверхность через высоту и сторону основания
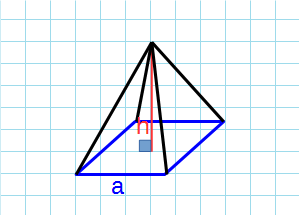
Формула площади боковой поверхности правильной пирамиды через высоту и сторону основания:
a — сторона основания; h — высота пирамиды; n — число сторон в основании.
Полная поверхность через высоту и сторону основания

Формула площади полной поверхности правильной пирамиды через высоту и сторону основания:
a — сторона основания; h — высота пирамиды; n — число сторон в основании.
Полная площадь тетраэдра
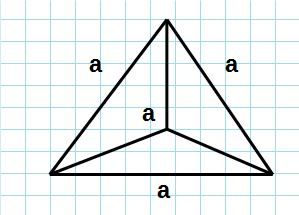
Формула полной площадь тетраэдра:
a — сторона основания.
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Формула для вычисления площади поверхности правильной пирамиды
Через периметр, площадь и апофему $S_{text {полн }}=frac{1}{2} P L+S_{text {осн }}$, где:
P — периметр основания
S — площадь основания
L — апофема пирамиды
Через стороны и высоту $left.S=frac{n cdot a}{2}left(frac{a}{2 cdot operatorname{tg}left(frac{180^{circ}}{n}right)}+sqrt{h^{2}+left(2 cdot operatorname{tg}left(frac{180^{circ}}{n}right)right.}right)^{2}right)$, где:
n — число сторон основания
a — длина стороны основания
h — высота пирамиды
Площадь поверхности пирамиды. В этой статье мы рассмотрим с вами задачи с правильными пирамидами. Напомню, что правильная пирамида – это пирамида, основанием которой является правильный многоугольник, вершина пирамиды проецируется в центр этого многоугольника.
Боковая грань такой пирамиды это равнобедренный треугольник. Высота этого треугольника, проведенная из вершины правильной пирамиды, называется апофемой, SF – апофема:
В представленном ниже типе задач требуется найти площадь поверхности всей пирамиды или площадь её боковой поверхности. На блоге уже рассмотрено несколько задач с правильными пирамидами, где ставился вопрос о нахождении элементов (высоты, ребра основания, бокового ребра), можете посмотреть.
В типовых заданиях, как правило, рассматриваются правильные треугольные, четырёхугольные и шестиугольные пирамиды. Задач с правильными пятиугольными и семиугольными пирамидами пока не встречал.
Кстати, на проекте youclever неплохой визуальный гид по пирамиде: с красивыми картинками, основными формулами и свойствами. Подходит тем, кто лучше воспринимает информацию визуально. Там весь учебник по геометрии такой — мало задач, но много понятных рисунков.
Формула площади всей поверхности проста — требуется найти сумму площади основания пирамиды и площади её боковой поверхности:
Рассмотрим задачи:
Стороны основания правильной четырехугольной пирамиды равны 72, боковые ребра равны 164. Найдите площадь поверхности этой пирамиды.
Площадь поверхности пирамиды равна сумме площадей боковой поверхности и основания:
*Боковая поверхность состоит из четырёх равных по площади треугольников. Основание пирамиды это квадрат.
Площадь боковой стороны пирамиды можем вычислить воспользовавшись формулой Герона:
Таким образом, площадь поверхности пирамиды равна:
Ответ: 28224
Стороны основания правильной шестиугольной пирамиды равны 22, боковые ребра равны 61. Найдите площадь боковой поверхности этой пирамиды.
Основанием правильной шестиугольной пирамиды является правильный шестиугольник.
Площадь боковой поверхности данной пирамиды состоит из шести площадей равных треугольников с сторонами 61,61 и 22:
Найдём площадь треугольника, воспользуемся формулой Герона:
Таким образом, площадь боковой поверхности равна:
Ответ: 3240
*В представленных выше задачах площадь боковой грани можно было найти используя другую формулу треугольника, но для этого нужно вычислить апофему.
27155. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
Для того, чтобы найти площадь поверхности пирамиды нам необходимо знать площадь основания и площадь боковой поверхности:
Площадь основания равна 36, так как это квадрат со стороной 6.
Боковая поверхность состоит из четырёх граней, которые являются равными треугольниками. Для того, чтобы найти площадь такого треугольника требуется знать его основание и высоту (апофему):
*Площадь треугольника равна половине произведения основания и высоты проведённой к этому основанию.
Основание известно, оно равно шести. Найдём высоту. Рассмотрим прямоугольный треугольник (он выделен жёлтым):
Один катет равен 4, так как это высота пирамиды, другой равен 3, так как он равен половине ребра основания. Можем найти гипотенузу, по теореме Пифагора:
Значит площадь боковой поверхности пирамиды равна:
Таким образом, площадь поверхности всей пирамиды равна:
Ответ: 96
27069. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Посмотреть решение
27070. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Посмотреть решение
Существуют ещё формулы площади боковой поверхности правильной пирамиды. В правильной пирамиде основание является ортогональной проекцией боковой поверхности, поэтому:
где φ — двугранный угол при основании
Отсюда площадь полной поверхности правильной пирамиды может быть найдена по формуле:
Еще одна формула боковой поверхности правильной пирамиды:
P — периметр основания, l — апофема пирамиды
*Эта формула основывается на формуле площади треугольника.
Если хотите узнать подробнее как эти формулы выводятся, не пропустите, следите за публикацией статей. На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.