Как найти площадь поверхности прямоугольного параллелепипеда егэ

Всего: 20    1–20

Добавить в вариант

Объем куба равен 8. Найдите площадь его поверхности.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.

Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.

Объем куба равен 8. Найдите площадь его поверхности.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.

Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его площадь поверхности.

Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности.

Площадь поверхности куба равна 24. Найдите его объем.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.

Объем первого куба в 8 раз больше объема второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2 и 7. Найдите его площадь поверхности.

Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 5 и 7. Найдите его площадь поверхности.

Площадь поверхности куба равна 864. Найдите его объем.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 12 и 12. Диагональ параллелепипеда равна 18. Найдите площадь поверхности параллелепипеда.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 7 и 4. Объем параллелепипеда равен 140. Найдите площадь его поверхности.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 8 и 5. Объем параллелепипеда равен 280. Найдите площадь его поверхности.

Объем одного куба в 729 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Объем одного куба в 125 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Всего: 20    1–20

Источник

Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

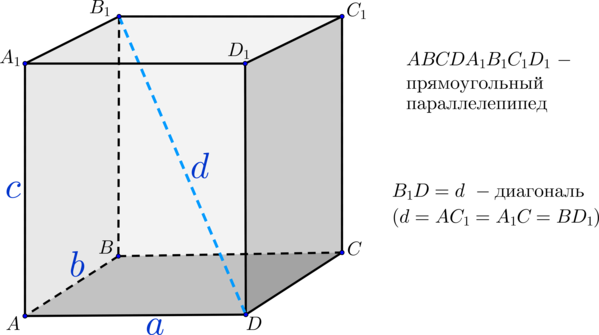
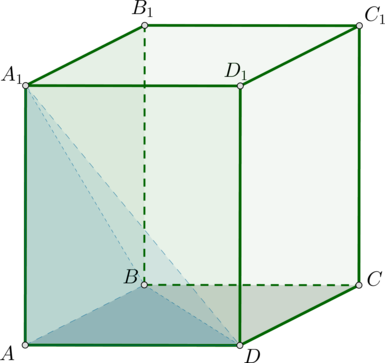
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.

Свойства прямоугольного параллелепипеда:

  1. В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
  2. Противоположные грани попарно равны и параллельны.
  3. Все двугранные углы прямоугольного параллелепипеда – прямые.
  4. Диагонали прямоугольного параллелепипеда равны.
  5. Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
  6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
  7. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
  8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

$B_1D^2=AD^2+DC^2+C_1C^2$

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$а$ — длина;

$b$ — ширина;

$с$ — высота(она же боковое ребро);

$P_{осн}$ — периметр основания;

$S_{осн}$ — площадь основания;

$S_{бок}$ — площадь боковой поверхности;

$S_{п.п}$ — площадь полной поверхности;

$V$ — объем.

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

$S_{бок}=P_{осн}·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.

$S_{п.п}=2(ab+bc+ac).$

Дополнительные сведения, которые пригодятся для решения задач:

Куб

$а$ — длина стороны.

$V=a^3;$

$S_{бок}=4а^2;$

$S_{п.п}=6а^2;$

$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Объем любой пирамиды равен трети произведения основания и высоты.

$V={1}/{3}S_{осн}·h$

В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

Площадь треугольника.

  • $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$.
  • $S={a·b·sin⁡α}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
  • Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$.
  • $S=p·r$, где $r$ — радиус вписанной окружности.
  • $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности.
  • Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
  • Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ — длина стороны. 

В основании лежит четырехугольник.

  1. Прямоугольник.
    $S=a·b$, где $а$ и $b$ — смежные стороны.
  2. Ромб.
    $S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба.
    $S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
  3. Трапеция.
    $S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
  4. Квадрат.
    $S=a^2$, где $а$ — сторона квадрата.

Пример:

Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.

Решение:

Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.

Объем пирамиды, в основании которой лежит прямоугольник

$V={S_{прямоугольника}·h}/{3}={a·b·h}/{3}$, где $a$ и $b$ — стороны прямоугольника.

Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.

В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.

Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).

$СС_1=АА_1=4$

$V={А_1В_1·A_1D_1·СС_1}/{3}={8·12·4}/{3}=128$

Ответ: $128$

Теорема Пифагора.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Источник

Формулы объёма и площади поверхности. Многогранники.

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

  1. Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
  2. Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.


Куб 		V=a^3 S = 6a^2
d=asqrt{3}, d- диагональ

Параллелепипед 		V=S_text{OCH}h, h - высота

Прямоугольный параллелепипед 		V=abc S = 2ab+2bc+2ac
d=sqrt{a^2+b^2+c^2}

Призма 		V=S_text{OCH}h S = 2S_text{OCH}+

Пирамида 		V=frac{1}{3}S_text{OCH}h S = S_text{OCH}+

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Задача 1.Объём куба равен 12. Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение:

Пирамида в кубе
Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб :-)

Очевидно, их 6, поскольку у куба 6 граней.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Разберем задачи, где требуется найти площадь поверхности многогранника.

Мы рассмотрим призмы и пирамиды. Начнем с призмы.

Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.

Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.

Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Пирамида в кубе

Решение.

Многогранник на рисунке – это прямая призма с высотой 12.

P_text{OCH}=8+6+6+2+2+4=28.

Пирамида в кубе

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

S_1=6cdot 6=36 (больший квадрат), S_2=2cdot 4=8 (маленький прямоугольник), S_text{OCH}=36+8=44

Подставим все данные в формулу: и найдем площадь поверхности многогранника:

S=28cdot12+2cdot44=336+88=424.

Ответ: 424.

Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Пирамида в кубе

Решение.

Пирамида в кубе

Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:

P_text{OCH}=4+5+2+1+2+4=18.

Пирамида в кубе

Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:

S_1=4cdot4=16;~S_2=2cdot1=2 (большой прямоугольник), S_text{OCH}=16+2=18 (маленький прямоугольник).

Найдем площадь полной поверхности: =18cdot1+2cdot18=54

Ответ: 54

Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Пирамида в кубе

Решение.

Покажем еще один способ решения задачи.

Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.

И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:

S=((4+1+4+1)cdot 3+2cdot 4 cdot 1)+6cdot 1-2cdot 1=42.

Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.

Ответ: 42

Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.

Пирамида в кубе

Решение.

Пусть АВ = 5 см, ВС = 3 см, тогда angle{ABC}=120^{circ}

Из Delta ABC по теореме косинусов найдем ребро АС:

AC^2=AB^2+BC^2-2cdot ABcdot BC cdot cos120^{circ}

AC^2=25+9-2cdot5cdot3cdotleft(-frac{1}{2}right)=47, ~AC = 7

Отрезок АС – большая сторона Delta ABC, следовательно, ACC_1A_1 - большая боковая грань призмы.

Поэтому ACcdot CC_1=35, или 7cdot h=35, откуда h=5.

(5+3+7)cdot5=75.

Ответ: 75

Теперь две задачи на площадь боковой поверхности пирамиды.

Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.

Пирамида в кубе

Решение.

Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.

Проведем AKperp BC, тогда BC perp DK (по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.

Delta ABC – равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.

Из прямоугольного Delta ABK получим:

AK=sqrt{AB^2-BK^2}=sqrt{13^2-5^2}=sqrt{169-25}=sqrt{144}=12.

Из прямоугольного Delta DAK имеем:

DK=sqrt{DA^2+AK^2}=sqrt{9^2+12^2}=sqrt{81+144}=sqrt{225}=15.

Delta ADB=Delta ADC (по двум катетам), тогда S_{ADB}=S_{ADC}, следовательно

=2S_{ADB}+S_{BDC},=2cdotfrac{1}{2}cdot13cdot9+frac{1}{2}cdot10cdot15=117+75=192.

Ответ: 192

Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.

Пирамида в кубе

Решение:

Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.

Площадь поверхности пирамиды равна

=pcdot h+a^2, где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.

Значит, полупериметр основания p = 24 cdot 2 = 48.

Апофему найдем по теореме Пифагора:

h=sqrt{37^2-12^2}=sqrt{(37-12)(37+12)}=sqrt{25cdot49}=5cdot7=35

S = 48cdot 35+24^2=1680+576=2256.

Ответ: 2256

Как решать задачи на нахождение объема многогранника сложной формы?

Покажем два способа.

Первый способ

1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.

Второй способ.

1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.

Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Пирамида в кубе

Решение.

Пирамида в кубе

1) Достроим составной многогранник до параллелепипеда.

2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту: V=9cdot 4cdot10=360

3) Найдем объем лишней части, то есть маленького параллелепипеда.

Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем V_1=5cdot4cdot7=140.

4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры: V=360-140=220.

Ответ: 220.

Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.

Пирамида в кубе

Объем призмы равен V=S_{OCH}cdot h, а так как призма прямая, то ее боковое ребро является и высотой, то есть h=6.

Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания

S_{OCH}=frac{1}{2}cdot ab=frac{1}{2}cdot6cdot7=21.

V=21cdot6=126.

Ответ: 126

Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.

Пирамида в кубе

Решение.

Объем призмы равен V = S_{OCH}cdot h

Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.

Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в 9^2 = 81 раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.

Объем воды не изменился, V=S_1cdot h_1=S_2 cdot h_2. Так как S_2=81S_1, высота воды h_2 должна быть в 81 раз меньше, чем h_1. Она равна 324:81 = 4 (см).

Ответ: 4

Задача 12. Объем параллелепипеда ABCDA_1B_1C_1D_1. Найдите объем треугольной пирамиды ABDA_1.

Пирамида в кубе

Решение.
Опустим из вершины A_1 высоту A_1H Н на основание ABCD.

=S_{ABCD}cdot A_1H

=frac{1}{3}S_{ABD}cdot A_1H

Пирамида в кубе

Диагональ основания делит его на два равных треугольника, следовательно, S_{ABD}=frac{1}{2}S_{ABCD}.

Имеем:

ABDA_1=frac{1}{3}S_{ABD}cdot A_1H=frac{1}{3}cdotfrac{1}{2}S_{ABCD}cdot A_1H=frac{1}{6}V_{ABCDA_1B_1C_1D_1}=frac{1}{6}cdot21=3,5.

Ответ: 3,5

Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна 6sqrt{3}.

Пирамида в кубе

Решение.
По формуле объема пирамиды, .

В основании пирамиды лежит правильный треугольник. Его площадь равна S_{OCH}=frac{a^2sqrt{3}}{4}.

S_{OCH}=frac{8^2sqrt{3}}{4}=frac{64sqrt{3}}{4}=16sqrt{3}.

Объем пирамиды V=frac{1}{3}cdot16sqrt{3}cdot6sqrt{3}=16cdot6=96.

Ответ: 96

Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.

Пирамида в кубе

Решение.

По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.

Пусть AD=x, тогда S_{OCH}=x^2.

Так как точки М и К – середины АD и DС соответственно, то DM=DK=frac{x}{2}.

S_{MDK}=frac{1}{2}MDcdot DK=frac{1}{2}cdotfrac{x}{2}cdotfrac{x}{2}=frac{1}{8}x^2.

Площадь треугольника MDK, лежащего в основании новой призмы, составляет frac{1}{8} часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: V=S_{OCH}cdot h, и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен 32:8=4.

Ответ: 4

Докажем полезную теорему.

Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

Доказательство:

Пирамида в кубе

Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.

S=a_1l+a_2l+dots+a_nl,

S=(a_1+a_2+dots+a_n)l,

S=P_{perp}cdot l.

Больше задач на формулы объема и площади поверхности здесь.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

8. Геометрия в пространстве (стереометрия)


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Задачи по теме «Прямоугольный параллелепипед»

(blacktriangleright) Прямоугольный параллелепипед – это параллелепипед, все грани которого являются прямоугольниками.
Другими словами, это прямая призма, основания которой – прямоугольники.
(эти определения эквивалентны).

Тогда:

1) противоположные грани равны между собой;

2) боковые ребра перпендикулярны основаниям, то есть являются высотами;

3) как следствие, формула для объема принимает вид: ({Large{V=abc}}), где (a, b, c) – три различных боковых ребра.

(blacktriangleright) Диагональ прямоугольного параллелепипеда – это отрезок, соединяющий две противоположные (не лежащие в одной грани) вершины.

1) Все диагонали равны, пересекаются в одной точке и делятся ею пополам;

2) Диагональ (d) можно найти по формуле: ({Large{d^{,2}=a^2+b^2+c^2}}).


Задание
1

#2863

Уровень задания: Легче ЕГЭ

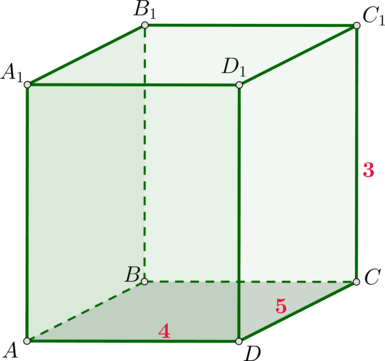
Дан прямоугольный параллелепипед, стороны основания которого равны (4) и (5), а боковое ребро равно (3). Найдите наибольшую площадь его грани.

Заметим, что все варианты для площадей его граней – это всевозможные попарные произведения чисел (3,4,5), то есть (3cdot
4), (4cdot 5) или (3cdot 5). Среди этих произведений наибольшим является (4cdot 5=20).

Ответ: 20


Задание
2

#2864

Уровень задания: Легче ЕГЭ

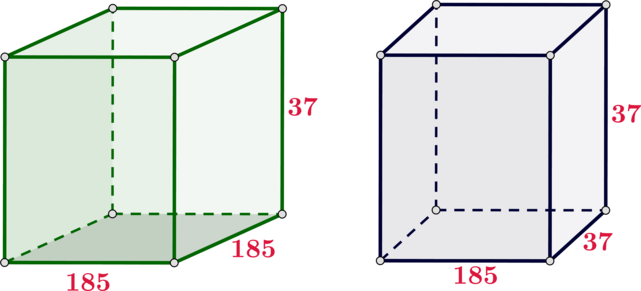
Даны два прямоугольных параллелепипеда: ребра одного равны (185), (185) и (37); а ребра другого равны (185, 37) и (37). Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда?

Отношение их объемов равно: [dfrac{V_1}{V_2}=dfrac{185cdot 185cdot 37}{185cdot 37cdot 37}=
dfrac{185}{37}=5.]

Ответ: 5


Задание
3

#2865

Уровень задания: Легче ЕГЭ

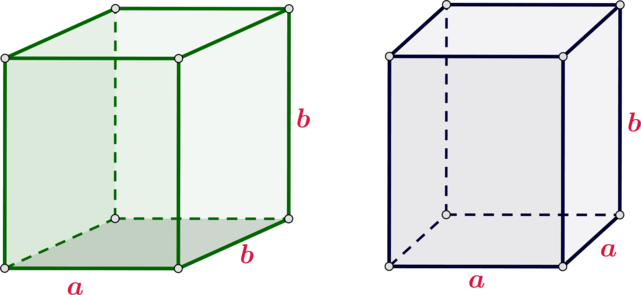
Даны два прямоугольных параллелепипеда: ребра одного равны (a, b) и (b), а ребра другого равны (a, a) и (b). На сколько площадь полной поверхности первого параллелепипеда больше, чем площадь поверхности второго параллелепипеда, если (a=1000, b=1001).

Площадь полной поверхности первого параллелепипеда [S_1=2(ab+b^2+ab)] Площадь полной поверхности второго параллелепипеда [S_2=2(ab+ab+a^2)] Следовательно, [S_1-S_2=2(b^2-a^2)=2(b-a)(b+a)=2(1001-1000)(1001+1000)=4002.]

Ответ: 4002


Задание
4

#3974

Уровень задания: Равен ЕГЭ

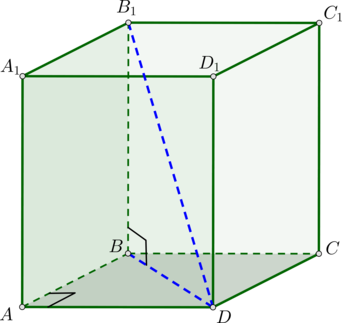
Дан прямоугольный параллелепипед (ABCDA_1B_1C_1D_1). Во сколько раз объем пирамиды (AA_1BD) меньше объема этого параллелепипеда?

Пусть (AB=x), (AD=y), (AA_1=z). Тогда объем параллелепипеда равен [V_{par}=S_{ABCD}cdot AA_1=xycdot z.] Так как (S_{ABD}=0,5S_{ABCD}) (потому что по определению прямоугольного параллелепипеда в основании лежит прямоугольник), то объем пирамиды [V_{pir}=dfrac13cdot S_{ABC}cdot AA_1=
dfrac13cdot dfrac12xycdot z=dfrac16xyz.] Следовательно, объем пирамиды в 6 раз меньше объема параллелепипеда.

Ответ:

6


Задание
5

#2867

Уровень задания: Равен ЕГЭ

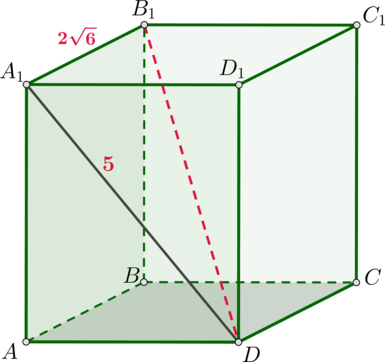
В прямоугольном параллелепипеде диагональ грани (AA_1D_1D) равна (5), а (AB=2sqrt6). Найдите диагональ параллелепипеда.

Так как параллелепипед прямоугольный, то все его грани – прямоугольники, а у прямоугольника обе диагонали равны. Следовательно, (A_1D=AD_1). Рассмотрим диагональ (A_1D) и диагональ параллелепипеда (B_1D). Треугольник (A_1B_1D) прямоугольный, так как ребро (A_1B_1) перпендикулярно грани (AA_1D_1D) (по определению прямоугольного параллелепипеда). Следовательно, гипотенуза [B_1D=sqrt{A_1B_1^2+A_1D^2}=sqrt{5^2+(2sqrt6)^2}=7.]

Ответ: 7


Задание
6

#2641

Уровень задания: Равен ЕГЭ

Дан прямоугольный параллелепипед с ребрами (2, 3) и (6). Найдите его диагональ.

Пусть (AB=2, AD=3 , AA_1=6).

По теореме Пифагора из прямоугольного треугольника (ABD) ((angle
A=90^circ)) имеем: (BD^2=AB^2+AD^2).

Из прямоугольного треугольника (BB_1D) ((angle B=90^circ)) по теореме Пифагора (B_1D^2=BD^2+BB_1^2).

Подставляя (BD^2) из первого равенства во второе, получим:

[B_1D^2=AB^2+AD^2+BB_1^2=2^2+3^2+6^2=4+9+36=49 quad Leftrightarrow quad B_1D=7.]

Ответ: 7


Задание
7

#2689

Уровень задания: Равен ЕГЭ

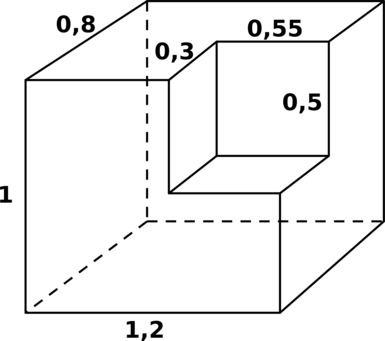
Найдите объём фигуры, получившейся после удаления маленького прямоугольного параллелепипеда из большого.

Объём оставшейся фигуры равен разности объёмов большого прямоугольного параллелепипеда (каким он был до удаления) и маленького (удалённого).

Таким образом, искомый объём равен [0,8cdot 1cdot 1,2 — 0,3cdot 0,5cdot 0,55 = 0,8775,.]

Ответ: 0,8775

Учащимся старших классов будет полезно научиться решать задачи ЕГЭ на нахождение объема и других неизвестных параметров прямоугольного параллелепипеда. Опыт предыдущих лет подтверждает тот факт, что подобные задания являются для многих выпускников достаточно сложными.

При этом понимать, как найти объем или площадь прямоугольного параллелепипеда, должны старшеклассники с любым уровнем подготовки. Только в этом случае они смогут рассчитывать на получение конкурентных баллов по итогам сдачи единого госэкзамена по математике.

Основные нюансы, которые стоит запомнить

  • Параллелограммы, из которых состоит параллелепипед, являются его гранями, их стороны — ребрами. Вершины этих фигур считаются вершинами самого многогранника.
  • Все диагонали прямоугольного параллелепипеда равны. Так как это прямой многогранник, то боковые грани представляют собой прямоугольники.
  • Так как параллелепипед — это призма, в основании которой находится параллелограмм, эта фигура обладает всеми свойствами призмы.
  • Боковые ребра прямоугольного параллелепипеда перпендикулярны основанию. Следовательно, они являются его высотами.

Готовьтесь к ЕГЭ вместе со «Школково»!

Чтобы занятия проходили легко и максимально эффективно, выбирайте наш математический портал. Здесь вы найдете весь необходимый материал, который потребуется на этапе подготовки к единому государственному экзамену.

Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию, основные формулы и элементарные задачи с решением, а затем постепенно переходим к заданиям экспертного уровня. Вы можете потренироваться, например, с решением задач на тему “Призма”.

Нужную базовую информацию вы найдете в разделе «Теоретическая справка». Вы также можете сразу приступить к решению задач по теме «Прямоугольный параллелепипед» в онлайн-режиме. В разделе «Каталог» представлена большая подборка упражнений разной степени сложности. База заданий регулярно пополняется.

Проверьте, легко ли вы сможете найти объем прямоугольного параллелепипеда, прямо сейчас. Разберите любое задание. Если упражнение дается вам легко, переходите к более сложным задачам. А если возникли определенные сложности, рекомендуем вам планировать свой день таким образом, чтобы ваше расписание включало занятия с дистанционным порталом «Школково».

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник

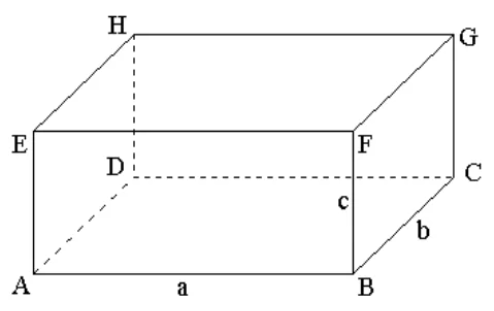
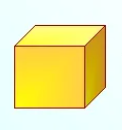
Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).

Рисунок 1

Определение

Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.

Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.

У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.

Рисунок 2

Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.

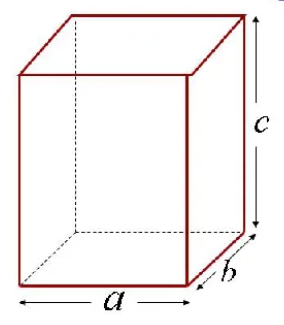
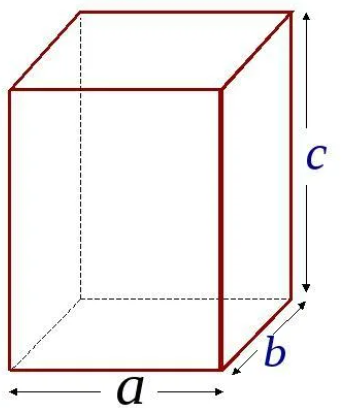
Длина, ширина, высота

Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.

Рисунок 3

Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.

Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.

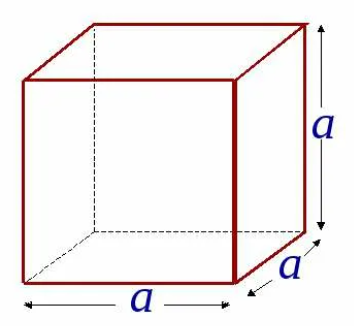
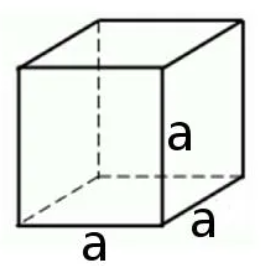
Куб

Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).

Рисунок 4

Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a2. Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a2

Объем прямоугольного параллелепипеда

Рисунок 5

С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.

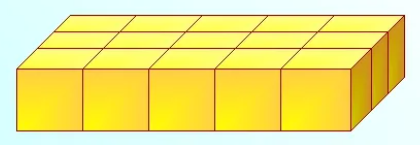
Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.

Рисунок 6

 

За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.

Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм3; с ребром 1 см – кубическим сантиметром (см3) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.

Формула объема прямоугольного параллелепипеда

Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.

Рисунок 7

Объем куба

Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:

V=a3

Рисунок 8

Пирамида

Рисунок 9

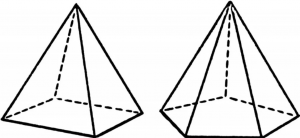
Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).

Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).

Рисунок 10

Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.

Рисунок 11

Даниил Романович | Просмотров: 1.1k

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти людей которые ищут работу
  • Капуста в голубцах жесткая что делать как исправить
  • Тестораскаточная машина рвет тесто как исправить
  • Как найти квадрат числа 100
  • Как найти судебный акт по постановлению