В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
- Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)
Формула получена следующим образом:
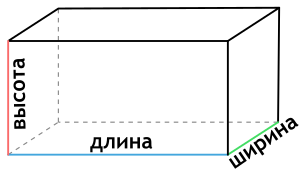
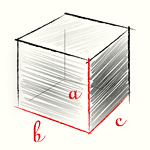
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.

{S_{полн} = 2(ab+bc+ac)}
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер — это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
В дополнение на сайте можно найти объем параллелепипеда.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота — это ребра прямоугольного параллелепипеда.
Содержание:
- калькулятор площади поверхности прямоугольного параллелепипеда
- формула площади поверхности прямоугольного параллелепипеда
- формула площади боковой поверхности прямоугольного параллелепипеда
- примеры задач
Формула площади поверхности прямоугольного параллелепипеда
{S_{полн} = 2(ab+bc+ac)}
a — длина прямоугольного параллелепипеда
b — ширина прямоугольного параллелепипеда
c — высота прямоугольного параллелепипеда
Формула площади боковой поверхности прямоугольного параллелепипеда
{S_{бок} = 2(ac+bc)}
a — длина прямоугольного параллелепипеда
b — ширина прямоугольного параллелепипеда
c — высота прямоугольного параллелепипеда
Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда
Задача 1
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.
Решение
Для нахождения площади поверхности воспользуемся первой формулой. Подставим в нее значения длины, ширины и высоты параллелепипеда и произведем вычисления.
S_{полн} = 2(ab+bc+ac) = 2(2 cdot 4 + 4 cdot 5 + 2 cdot 5) = 2(8 + 20 + 10) = 2(38) = 76 : см^2
Ответ: 76 см²
Проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3см 5см и 6см.
Решение
Задача аналогична предыдущей, поэтому повторим действия, подставив новые значения измерений параллелепипеда.
S_{полн} = 2(ab+bc+ac) = 2(3 cdot 5 + 5 cdot 6 + 3 cdot 6) = 2(15 + 30 + 18) = 2(63) = 126 : см^2
Ответ: 126 см²
Для проверки ответа используем калькулятор .
Задача 3
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 9м 24м 11м.
Решение
Еще одна типовая задача. Для ее решения также воспользуемся первой формулой.
S_{полн} = 2(ab+bc+ac) = 2(9 cdot 24 + 24 cdot 11 + 9 cdot 11) = 2(216 + 264 + 99) = 2(579) = 1158 : см^2
Ответ: 1158 см²
Проверка .
Задача 4
Найдите площадь боковой поверхности прямоугольного параллелепипеда у которого a=4см, b=5см, c=7см.
Решение
В этой задаче нам необхожимо найти площадь боковой поверхности. Поэтому мы будем использовать для ее решения вторую формулу.
S_{бок} = 2(ac+bc) = 2(4 cdot 7 + 5 cdot 7) = 2(28 + 35) = 2(63) = 126 : см^2
Ответ: 126 см²
Как всегда ответ можно проверить с помощью калькулятора .
Площадь поверхности прямоугольного параллелепипеда, формула.
Параллелепипедом называется призма, основание которой параллелограмм. Параллелепипед имеет шесть граней, и все они — параллелограммы.
Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым. Прямой параллелепипед у которого все шесть граней прямоугольники, называется прямоугольным.
Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме площадей трех граней этого параллелепипеда:
[S = 2(S_a+S_b+S_c) = 2(ab + bc + ac)]
(a,b,c — ребра параллелепипеда)
Вычислить, найти площадь поверхности прямоугольного параллелепипеда по формуле (1).
Площадь поверхности параллелепипеда |
стр. 323 |
|---|
Параллелепипед — это призма, в основании которой находится параллелограмм. Противоположные стороны параллелепипеда равны. Соответственно, у них будут и равные площади. Всего у параллелепипеда 6 граней, значит:
Sобщ = 2(S1+S2+S3)
Идем дальше. Примем, что ребра параллелограмма равны a, b и с. Где a, b — стороны основания (образуют S1), а с — высота параллелограмма. b и с образуют S2, а c и a образуют S3.
Далее: существует несколько различных случаев:
1) Если все шесть граней параллелепипеда являются прямоугольниками — то такой параллелепипед называется прямоугольным. И его площадь высчитывается по формуле:
Sобщ = 2(S1+S2+S3) = 2(ab + bс + aс)
2) Если четыре из шести граней параллелограмма являются прямоугольниками, то такой параллелепипед называется прямым. Его площадь считается не только через длину его ребер, но и через величину непрямого угла между сторонами параллелограмма, не являющегося прямоугольником:
Sобщ = 2(S1+S2+S3) = 2(absinX + сb + aс)
3) Куб — тоже частный случай параллелограмма. Это прямоугольный параллелограмм, все ребра которого равны. Соответственно, будут равны и все стороны. Площадь высчитывать легче всего:
Sобщ = 2(S1+S2+S3) = 2(a^a+а^2+a^2)=6a^2, где а — ребро куба.
Общая формула площади поверхности параллелограмма в полном варианте применяется в тех случаях, когда он не является прямоугольным. Ребра такой призмы расположены не под прямым углом друг к другу, а значит синус этих углов не равен единице, как в предыдущих случаях, когда мы его просто не указывали.
Если допустить, что углы между ребрами параллелограмма равны:
- угол между а и b = X
- угол между а и c = Y
- угол между c и b = Z
Тогда:
Sобщ = 2(S1+S2+S3) = 2(absinX + сbsinZ + aсsinY)
Далее можно упомянуть еще один вид параллелограммов: те, у которых лишь две стороны являются прямоугольниками. Допустим, что S1 — это площадь прямоугольника в основании. Тогда:
Sобщ = 2(S1+S2+S3) = 2(absinX + сbsinZ + aсsinY) = 2(ab + сbsinZ + aсsinY), т.к. Х=90 градусов и sinX=1.
Вот как-то так)
Как найти площадь поверхности прямоугольного параллелепипеда
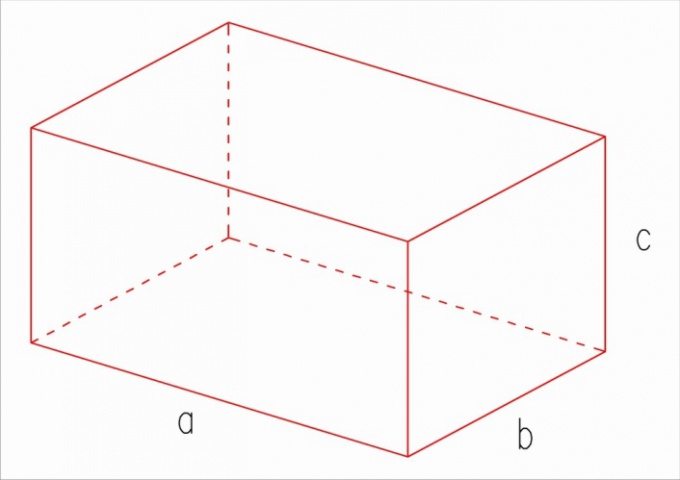
Прямоугольным называется такой параллелепипед, все шесть граней которого являются прямоугольниками. Формула расчета площади его поверхности очень проста: S = 2(ab + bc + ac), где a, b и c – длины ребер.
Инструкция
Для начала вычислите площади трех разных граней параллелепипеда. Например, длина параллелепипеда (а) равна 7 см, ширина (b) – 6 см, а высота (с) – 4 см. Тогда площадь верхней (нижней) грани будет равна ab, т.е. 7х6=42 см. Площадь одной из боковых граней будет равна bc, т.е. 6х4=24 см. Наконец, площадь передней (задней) грани будет равна ac, т.е. 7х4=28 см.
Теперь сложите вместе все три результата и умножьте полученную сумму на два. В нашем это будет выглядеть следующим образом: 42+24+28=94; 94х2=188. Таким образом, площадь поверхности данного прямоугольного параллелепипеда будет равна 188 см.
Обратите внимание
Будьте внимательны и не путайте прямоугольный параллелепипед с прямым. У прямого параллелепипеда прямоугольниками являются только боковые стороны (4 из 6-ти граней), а верхнее и нижнее основания – произвольные параллелограммы.
Полезный совет
В качестве частного случая прямоугольного параллелепипеда может рассматриваться куб. Так как все его грани равны, то для нахождения его поверхности будет необходимо возвести длину ребра в квадрат и умножить на 6.
Источники:
- Онлайн-калькулятор, рассчитывающий площадь поверхности прямоугольного параллелепипеда
- как находить прямоугольный параллелепипед
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.