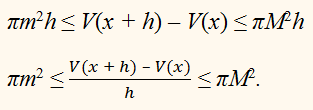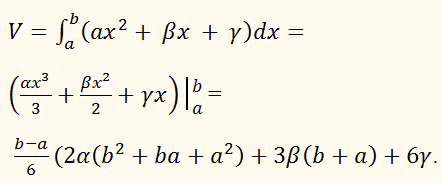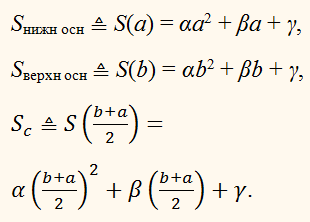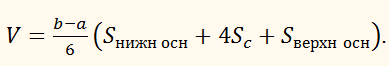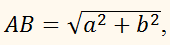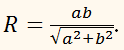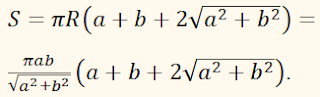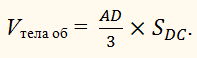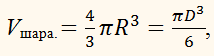Как найти площадь поверхности тела вращения треугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Тела и поверхности вращения. Шар. Цилиндр. Конус

Тела и поверхности вращения.

Шар. Цилиндр. Конус. Площади поверхности и объемы этих фигур.

Подробная теория с наглядными иллюстрациями и основные формулы.

Читай эту статью, здесь все это есть.

Всего за 15 минут ты полностью во всём разберешься!

Тело вращения – это тело в пространстве, которое возникает при вращении какой-нибудь плоской фигуры вокруг какой-нибудь оси.

Вот самый простой пример: цилиндр.

Берем прямоугольник и начинаем вращать его вокруг одной из сторон.

Смотри.

Было–вращаем–стало:

А теперь гораздо хитрее. Бывает так, что ось вращения находится далеко от фигуры, которая вращается.

Например, так:

Вращаем:

Что получится? Бублик. А по-научному – ТОР.

Ну и так вот можно любую фигуру вертеть вокруг любой оси, и будут получаться разные более или менее сложные тела вращения.

Ну, а поверхность вращения – это просто граница тела вращения. Ведь поверхность это всегда граница тела.

Здесь мы рассмотрим подробно несколько тел вращения. Те, которые встречаются в школьных задачах. Это шар, цилиндр и конус.

Шар

Шар – тело вращения, полученное вращением полуокружности вокруг диаметра.

Было–вращаем–стало:

Вообще-то есть и другое определение шара – через ГМТ (геометрическое место точек)

Шар – геометрическое место точек, удаленных от одной фиксированной точки на расстояние, не более заданного.

Скажу тебе по секрету, что, хоть второе определение и пугающее на вид, оно удобнее в обращении. Задумайся, ведь если тебя попросят сказать, что такое шар, ты скажешь что-то вроде:

«ну …там есть центр и радиус…», подразумевая, что все точки внутри шара находятся я на расстоянии не большем, чем радиус.

Ну, в общем, шар он и есть шар.

Названия, которые ты должен знать:

Незнакомое тебе, наверное, только одно.

Диаметральное сечение шара – сечение, проходящее через центр. Это сечение иногда еще называют большим кругом.

А вообще:

Любое сечение шара – круг.
Граница шара называется сфера. (Так же, как граница круга – окружность.)

Площадь поверхности сферы

( {{S}_{поверхности }}=4pi {{R}^{2}})

( R) – радиус

Откуда взялось? Умные математики придумали – это не так уж просто – придется просто запомнить.

Объем шара

( {{V}_{шара}}=frac{4}{3}pi {{R}^{3}})

( R) – радиус

Это еще одна хитрая формула, которую придется запомнить, не понимая, откуда она взялась.

Если ты знаком с производной, то можешь заметить это:

( {{V’}_{шара}}={{S}_{поверхности}})

И это не случайно! Но почему это так вышло, мы тоже здесь обсуждать не будем. Можешь попробовать доказать это сам!

Цилиндр

Цилиндр – тело, образованное вращением прямоугольника вокруг одной из сторон.

Вообще-то, полное имя этого тела – «прямой круговой цилиндр», но составители задач и мы вместе с ними по дружбе называем его просто цилиндром. Названия, относящиеся к цилиндру, такие:

Основания у цилиндра – это круги

Еще у цилиндра есть так называемая развертка.

Представь, что у нас от цилиндра осталась только боковая поверхность, и мы ее разрезали вдоль образующей и развернули.

Что получится? Представь себе, прямоугольник.

Развертка цилиндра – прямоугольник.

Площадь боковой поверхности цилиндра

( {{S}_{бок.}}=2pi RH)

( R) – радиус

( H) – высота, она же образующая.

Откуда взялась эта формула? Это как раз легко! Именно потому, что цилиндр можно развернуть, и получится прямоугольник ( 2pi Rcdot H).

Площадь этого прямоугольника и есть площадь боковой поверхности цилиндра.

Площадь прямоугольника, как мы хорошо помним равна произведению сторон, поэтому

( {{S}_{бок.}}=2pi RH)

Площадь полной поверхности цилиндра

Прибавляем теперь площадь двух кругов – оснований и получаем:

( {{S}_{полн .}}=2pi RH+2pi {{R}^{2}})

Можно вынести (хотя и не обязательно) ( 2pi R):

( {{S}_{полн .}}=2pi Rleft( H+R right))

Но эту формулу неудобно запоминать!

Гораздо проще запомнить, что полная поверхность – сумма боковой поверхности и еще двух кругов – оснований, а боковая поверхность – прямоугольник. И тогда ( {{S}_{полн .}}) можно вообще не запоминать, ты всегда сам напишешь, что

( {{S}_{полн .}}=underbrace{2pi RH}_{прямоугольник}+underbrace{2pi {{R}^{2}}}_{два круга})

Объем цилиндра

( V=pi {{R}^{2}}H)

( R) – радиус основания ( H) – высота

Это точно как у призмы и параллелепипеда!

( V={{S}_{основания}}cdot H), только у призмы и параллелепипеда ( {{S}_{основания}}) — это площадь многоугольника, а у цилиндра ( {{S}_{основания}}) — это площадь круга.

Конус

Конус – тело вращения, образованное вращением прямоугольного треугольника вокруг одного из катетов.

Было–вращаем–стало:

И опять же, полное название этого тела: «прямой круговой конус», но во всех задачах у нас говорится просто «конус».

Названия, относящиеся к конусу:

Что тут нужно твердо помнить?

Основание корпуса – круг
Все образующие конуса – равны.

Ясно ли это? Вроде должно быть ясно, ведь образующая – это гипотенуза (одна и та же!) Треугольника, который вращаем, а радиус основания – катет.

У конуса тоже есть развертка.

Снова представим, что основания нет, разрежем боковую поверхность вдоль образующей и развернём кулек. Что получится?

Представь себе сектор круга. Пусть длина образующей равна ( l).

Развертка конуса – сектор круга радиуса ( l)

Площадь поверхности конуса

Как найти площадь боковой поверхности корпуса? Вспомним о развертке, ведь для цилиндра все было просто именно с помощью развертки.

По формуле площади сектора ( {{S}_{бок.}}={{l}^{2}}cdot frac{alpha }{2}) Где ( alpha ) – угол при вершине в радианах.

И это уже формула. В некоторых задачах бывает дан именно угол при вершине в развертке конуса.

Но если все же даны только образующая и радиус основания, как быть?

Нужно осознать, что же такое дуга в развертке? Это бывшая окружность основания! Поэтому длина этой дуги равна ( 2pi R).

С другой стороны, длина этой же дуги равна ( alpha cdot l), так как это дуга окружности радиуса ( l). Поэтому

( alpha cdot l=2pi R)

Подставляем

( {{S}_{бок.}}={{l}^{2}}cdot frac{alpha }{2}=frac{l}{2}cdot alpha cdot l=frac{l}{2}cdot 2pi R)

Итак,

( {{S}_{бок.}}=pi Rl), где

( R) — радиус окружности основания,

( l) — длина образующей

Ну, и осталось площадь полной поверхности конуса. Прибавим к боковой поверхности площадь круга основания, и получаем:

( {{S}_{полн. }}=pi Rl+pi {{R}^{2}})

Можно вынести ( pi R):

( {{S}_{полн. }}=pi Rleft( l+R right))

Но, как и для цилиндра, не надо запоминать вторую формулу, гораздо проще всегда пользоваться первой.

Объём конуса

( V=frac{1}{3}pi {{R}^{2}}H)

( R) – радиус основания (

H) – высота

Это так же, как у пирамиды

( V=frac{1}{3}{{S}_{осн.}}cdot H), только

( {{S}_{осн. }}) — это не площадь многоугольника, а площадь круга.

А вот откуда взялась ( frac{1}{3})?, по-прежнему остается загадкой, потому что эта ( frac{1}{3}) получена в результате довольно хитрых рассуждений умных математиков.

А тебе нужно очень твердо запомнить, что в формулах объёма «треугольных» фигур: конуса и пирамиды эта ( frac{1}{3}) и есть, а в формулах параллелепипеда, призмы и цилиндра ее нет!

Бонус: Вебинары по стереометрии из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 14 Стереометрия. Расстояние между точками и от точки до прямой

В этом видео мы научимся «видеть» 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).

Затем мы научимся двум основным вещам — находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.

На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии.

Не перескакивайте, не пропускайте его! Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.

ЕГЭ 14. Стереометрия. Пирамида. Разбор варианта профильного ЕГЭ 2020

В этом видео:

Как нарисовать шестиугольную пирамиду.
Как подписать вершины пирамиды чтобы потом легче было решать задачу.
Как исправить рисунок, если грани пирамиды сливаются.
Доказательство пунктов А и Б, а также их правильная запись, которую примет любой проверяющий на ЕГЭ.
Нахождение площади основания и объема пирамиды.
Самое главное, на что нужно обратить внимание.

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук — ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 — WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org — email для записи

тысячи учеников, поступивших в лучшие ВУЗы страны
автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
закончил МФТИ, преподавал на малом физтехе;
репетиторский стаж — c 2003 года;
в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».

Источник

Слайд 1Площадь поверхности
тел вращения

Слайд 2Основная цель:
сформиравать навык решения задач по

теме

Слайд 3

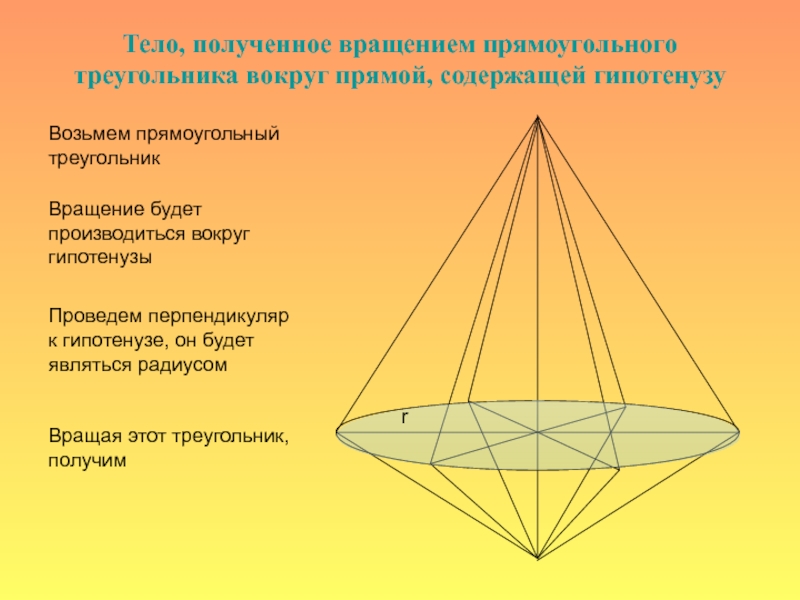
Тело, полученное вращением прямоугольного треугольника вокруг прямой,

содержащей гипотенузу
Возьмем прямоугольный треугольник
Вращение будет производиться вокруг

гипотенузы

Проведем перпендикуляр к гипотенузе, он будет являться радиусом

Вращая этот треугольник, получим

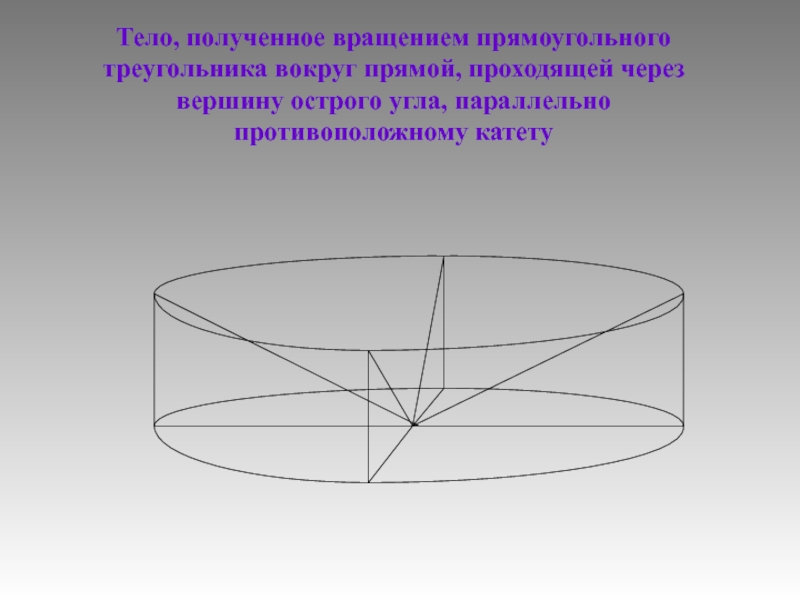
Слайд 4Тело, полученное вращением прямоугольного треугольника вокруг прямой,

проходящей через вершину острого угла, параллельно противоположному

катету

Слайд 5

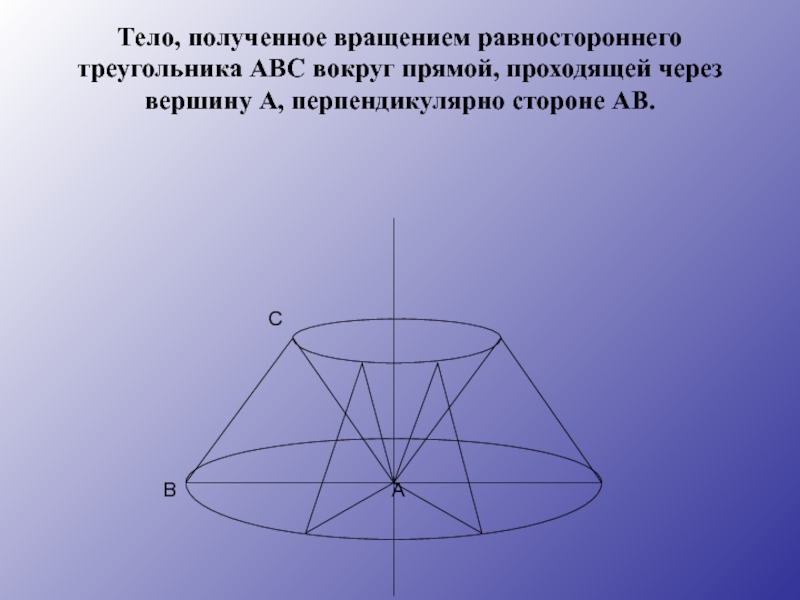
C

B A

Тело, полученное вращением равностороннего треугольника АВС вокруг прямой, проходящей через вершину А, перпендикулярно стороне АВ.

Слайд 6

Тело, полученное вращением равностороннего треугольника вокруг прямой,

содержащей одну из сторон треугольника

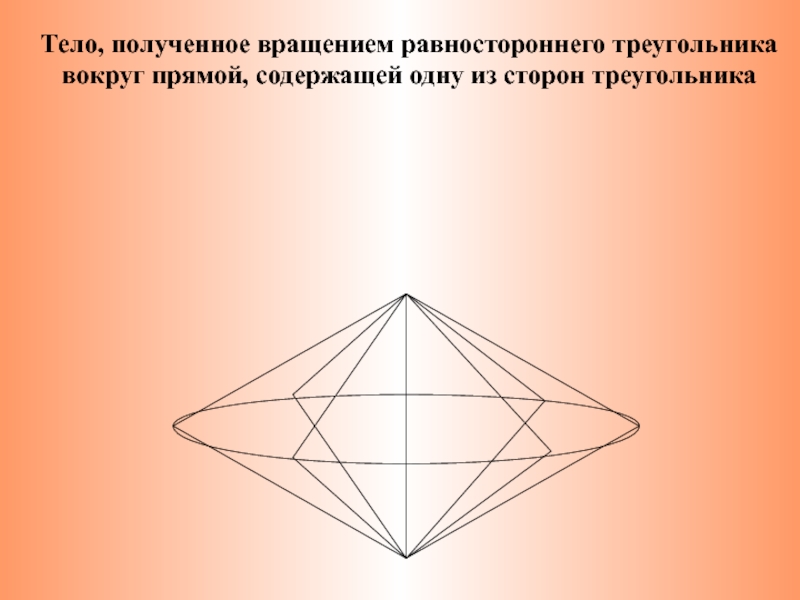
Слайд 7

Тело, полученное вращением тупоугольного равнобедренного треугольника вокруг

прямой, содержащей основание треугольника

Слайд 8

Тело, полученное вращением равностороннего треугольника вокруг прямой,

проходящей через вершину треугольника параллельно противолежащей стороне

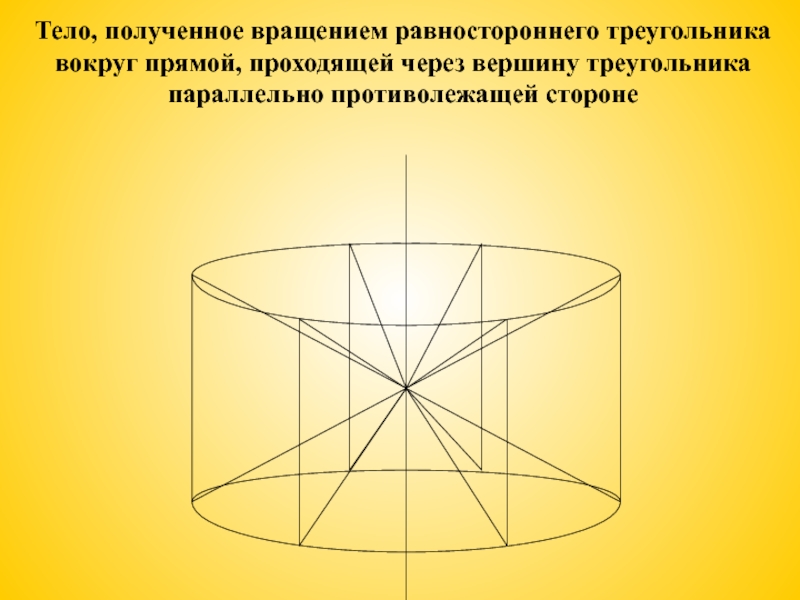
Слайд 9

Тело, полученное вращением прямоугольного треугольника вокруг прямой,

проходящей через вершину острого угла перпендикулярно гипотенузе

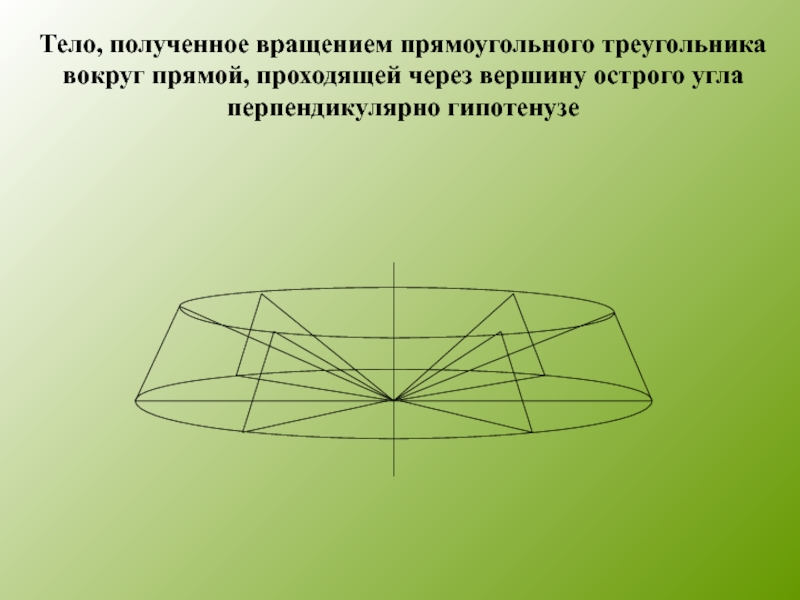
Слайд 10

Тело, полученное вращением прямоугольной трапеции вокруг прямой,

содержащей меньшую боковую сторону

Слайд 11

Тело, полученное вращением прямоугольной трапеции вокруг прямой,

содержащей меньшее основание

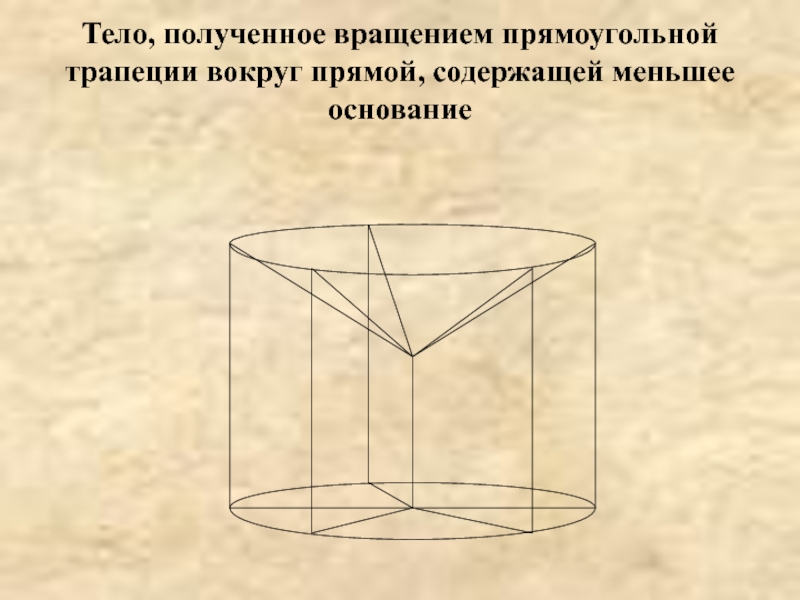
Слайд 12

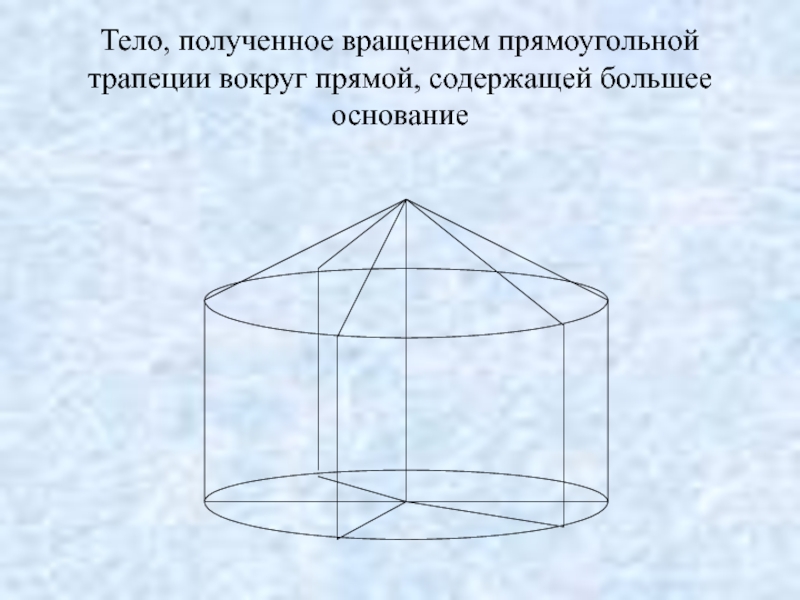
Тело, полученное вращением прямоугольной трапеции вокруг прямой,

содержащей большее основание

Слайд 13

Тело, полученное вращением равнобедренной трапеции вокруг прямой,

содержащей меньшее основание

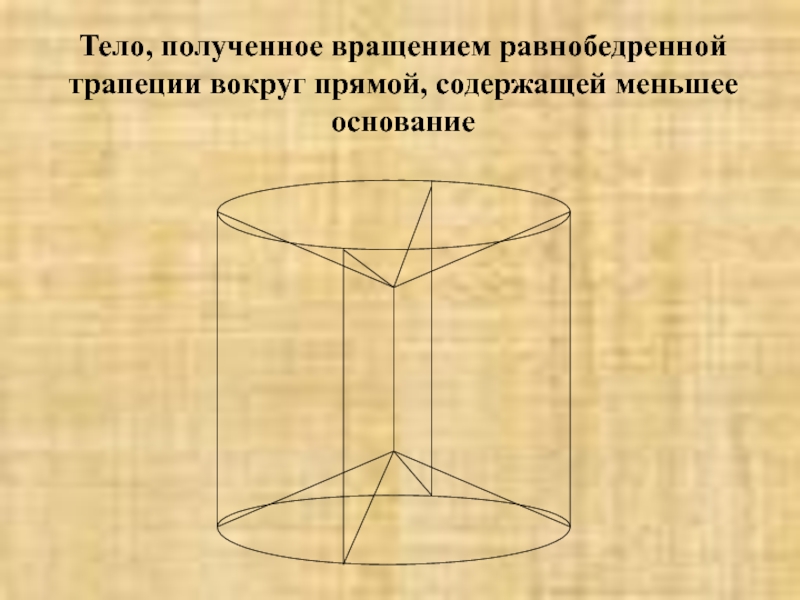
Слайд 14

Тело, полученное вращением равнобедренной трапеции вокруг прямой,

содержащей большее основание

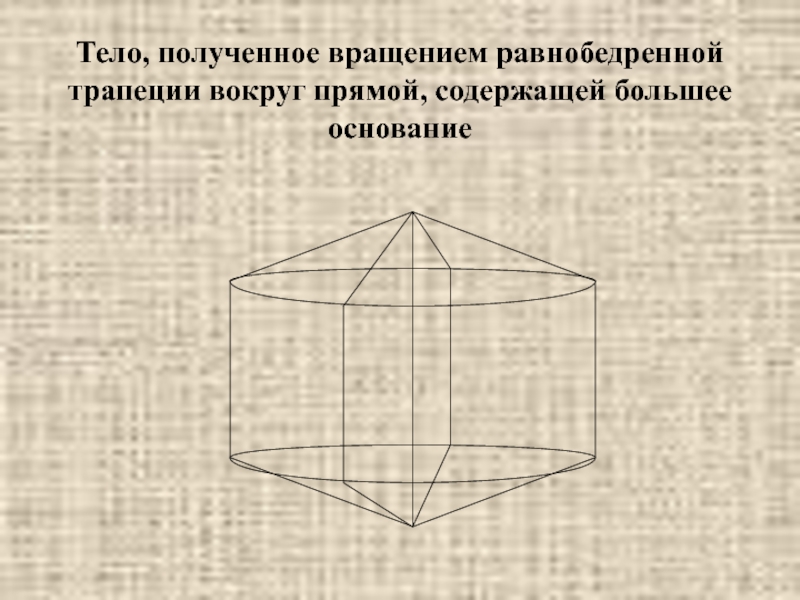
Слайд 15

Тело, полученное вращением ромба вокруг прямой, содержащей

сторону ромба

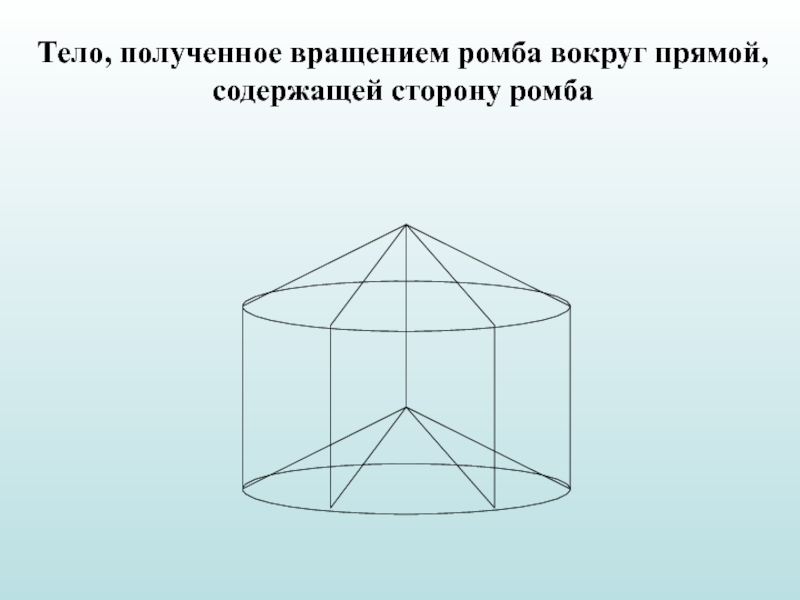
Слайд 16

Тело, полученное вращением ромба вокруг прямой, проходящей

через вершину ромба параллельно одной из диагоналей.

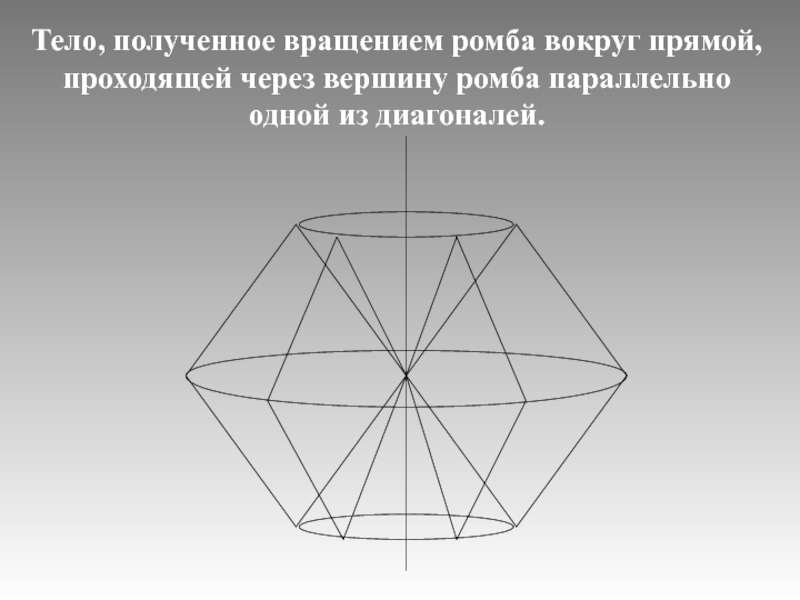
Слайд 17Задача 1
Прямоугольный треугольник с катетом 8

см и прилежащим к нему углом 30°

вращается вокруг прямой, содержащей гипотенузу. Найдите площадь поверхности полученного тела.

Так как r лежит напротив угла в 30°, то он равен половине гипотенузы.

Слайд 18Задача 2
Равнобедренный треугольник, у которого боковые

стороны равны по 4 см, а один

из углов 120°, вращается вокруг прямой, содержащей большую сторону. Найти площадь поверхности полученного тела.

Так как треугольник АВС равен треугольнику АВ1С, то

Так как r лежит напротив угла в 30°, то он равен половине гипотенузы r=2

Слайд 20Задача
В равнобедренной трапеции основания равны 14

и 50 см, а диагональ 40 см.

Эта трапеция вращается вокруг прямой, содержащей меньшее основание трапеции. Найдите площадь поверхности полученного тела.

Источник

Телом вращения в
самом простом случае называется такое тело, которое плоскостями,
перпендикулярными к некоторой прямой – оси вращения, пересекается по кругам с
центрами, которые лежат на этой прямой.

Круговой цилиндр,
конус, шар – примеры тел вращения.

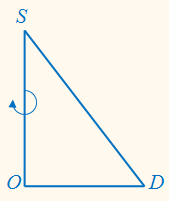
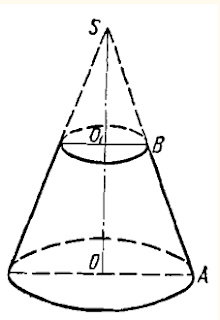
Конус можно
получить вращением прямоугольного треугольника вокруг одного из катетов.
Катет SO, вокруг которого происходит вращение, называется осью
конуса, а гипотенуза является образующей конуса. Кроме того, катет ОD равняется радиусу основы конуса, а катет SO равняется его высоте:

R = ОD, Н = SO.

Найдем формулу для
вычисления объема любого тела вращения.

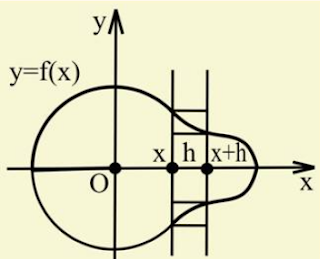
Проведем плоскость
через ось тела и введем в этой плоскости декартовые координаты х, y приняв ось тела
за ось х. Плоскость ху пересекает
поверхность тела по линии, для которой ось
х является осью симметрии.

Пусть y
= (х) – уравнение той части этой линии, которая расположена
над осью х. Проведем через точку
(х, 0) плоскость,
перпендикулярную оси х, и обозначим через
V(x) объём части тела, которая лежит влево от этой
плоскости, V(x) является функцией от х.
Разность

V(x + h)
– V(x)

представляет собой объем прослойки тела толщиной h,
заключительного между двумя плоскостями, которые перпендикулярны оси х и проходят через точки с абсциссами х и х + h. Пусть М – большее,
а m – наименьшее значение функции f(х)
на отрезке [x, x
+ h]. Тогда рассмотренная прослойка тела содержит цилиндр с
радиусом m и высотой h и находится в цилиндре с радиусом М и той же высотой h. Поэтому

При стремлении высоты
h к нулю левая и правая части последнего
неравенства стремятся к одной и той же величине
πf ²(x). Средняя ж часть этого
неравенства при стремлении h к 0 стремится к производной

V‘(x)
функции V(x). Виходить,

V‘(x) = πf
²(x).

По известной формуле

Эта формула и даёт
объём части тела, заключённого между параллельными плоскостями х = а и х
= b.

Формула Симпсона.

Если плоскость сечения S(x) тела Т перпендикулярная к оси Ох, то
функция х имеет вид

S(x) = αx²
+ βx + γ,

и объём такого тела,
которое находится между плоскостями

х = а и х
= b,

равен:

Обозначим площади сечений:

Тогда полученное ранее виражение для вычисления объёма тела Т можно представить в виде:

Эту формулу называют формулой Симпсона.

С помощью формулы
Симпсона легко получить выражения для вычисления объёмов тел, сечения которых плоскостью,
перпендикулярной оси Ох, можно представить в виде:

S(х)
= αх² + βх + γ.

Например, это объёмы
шара, пирамиды, конуса, так как соответствующие сечения этих тел соответствуют указанному
условию.

ПРИМЕР:

Для шара радиуса R имеем:

a = –R, b = R,

S(a) = S(b) = 0,
S_c = πR²,

ПРИМЕР:

В случае пирамиды:

a = 0, b = H,
S(a) = S₀,
S_c = (¹/₂)²S₀,

С помощью формулы Симпсона удобно
решать задачи на вычисление объёмов частей тел, которые
ограничены параллельными сечениями.

ПРИМЕР:

В случае усечённого конуса (с радиусами оснований R и r, высотой h) имеем:

a = 0, b = h,
S(a) = πR²,
S(b) = πr²,

Заметим, что при
вычислении S_c,
мы воспользовались тем, что осевым сечением усечённого конуса является
трапеция, средняя линия которой равняется диаметру сечения этого конуса
плоскостью

ЗАДАЧА:

Прямоугольный треугольник, катеты которого равны а и b, вращается
вокруг прямой, которая проходит через вершину прямого угла параллельно гипотенузе.
Найдите площадь поверхности тела вращения.

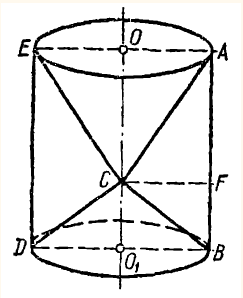
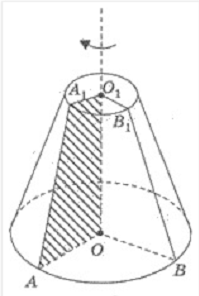
Прямоугольный ∆ABC (∠ C
= 90°) вращается вокруг прямой

OO₁ ∥ AB.

Точка С лежит на прямой OO₁. Найти площадь поверхности тела вращения, если

АС = b и ВС
= а.

Поверхность тела вращения будет
состоять из боковой поверхности цилиндра
ABDE и боковых поверхностей
конусов ACE и BCD. Образующую
цилиндра найдём из данного треугольника:

а радиусы оснований конусов и цилиндров,
которые равны между собой, определим из ∆ABC:

CF ×
AB = AC × CB.

Обозначив CF через R, найдём

Тогда поверхность тела вращения

ОТВЕТ:

Усечённый конус
может быть получен вращением прямоугольной трапеции вокруг боковой стороны,
перпендикулярной основанию.

Сторона ОО₁, вокруг которой вращается трапеция, называется осью усечённого
конуса, а вторая боковая сторона АВ трапеции – касательной
усечённого конуса. Основания трапеции будут соответственно радиусами нижнего и
верхнего основания усечённого конуса:

ОА = R, ВО₁ = r.

Поверхность, полученную
вращением большой стороны АА₁ трапеции
ОО₁А₁А называют боковой поверхностью усечённого
конуса.

Каждый отрезок этой
поверхности (а также его длина), который соединяет ближайшие точки окружностей
оснований усечённого конуса, называют образующими усечённого конуса. АА₁ и ВВ₁ –
образующие усечённого конуса. Они равны между собой.

Шар, так же как цилиндр и конус, является телом вращения. Он получается при
вращении полуокружности вокруг его диаметра как оси.

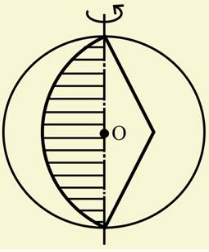
Если ось вращения совпадает с радиусом, который ограничивает круговой
сектор АОС, то полученный от вращения шаровой сектор называется
простым, а если ось вращения не совпадает с радиусом, который ограничивает
круговой сектор СОD,
то шаровой сектор называется полупустым.

Объём тела, полученного при вращении плоской фигуры вокруг оси.

Объём тела, описываемого плоской фигурой при вращении её вокруг
оси, лежащей в плоскости этой фигуры и не пересекающей её, равен произведению
площади фигуры на длину окружности, описываемой центром тяжести этой площади:

V_{тела об} =
2πSd_c,

где S – площадь вращающейся фигуры, а d_c– расстояние
от центра тяжести фигуры до оси вращения.

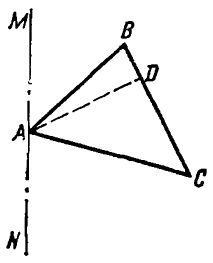
Если ∆ АВС вращается вокруг оси МN, которая
лежит в плоскости

треугольника, проходит через его вершину
А, но
не пересекает стороны ВС, то объём тела, полученного при этом вращении, равен произведению
поверхности S_ВС, образуемой противоположной стороной ВС,
на одну треть высоты треугольника, опущенной на эту сторону, то есть

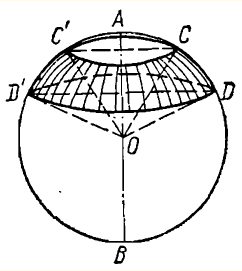
Объём шарового сектора и шара.

Объём шарового сектора, получаемого вращением вокруг диаметра МN кругового сектора АОВ, есть
предел, к которому стремится объём тела, образуемого вращением многоугольника, ограниченного
радиусами ОА и ОВ и правильной ломаной линией АСDВ.

Эта ломаная вписана в дугу кругового сектора, когда число сторон её неограниченно
увеличивается (и, следовательно, длина каждой из сторон АС, СD,
… стремится к нулю).

Объём шарового сектора равен произведению поверхности соответствующего
шарового пояса (или шарового
сегмента) на треть радиуса:

где R – радиус шарового сектора, а Н –
высота шарового пояса (сегмента).

Объём шара равен произведению его поверхности на треть
радиуса:

где R – радиус шара, D – диаметр шара.

Формулу для объёма шара получаем, положив в формуле для объёма шарового
сектора

Н = 2R.

Объём шарового сегмента равен объёму цилиндра, у которого радиус основания есть
высота сегмента, а высота цилиндра равна радиусу шара, уменьшенному на треть высоты
сегмента, то есть

где h – высота сегмента, а
R –
радиус шара.

Задания к уроку 16

Задание 1
Задание 2
Задание 3

Другие уроки:

Урок 1. Единицы измерения объёмов
Урок 2. Объём прямой призмы
Урок 3. Объём наклонной призмы
Урок 4. Объём правильной призмы
Урок 5. Объём прямого параллелепипеда
Урок 6. Объём наклонного параллелепипеда
Урок 7. Объём прямоугольногопараллелепипеда
Урок 8. Объём куба
Урок 9. Объём пирамиды
Урок 10. Объём правильной пирамиды
Урок 11. Объём усечённой пирамиды
Урок 12. Объём цилиндра
Урок 13. Объём конуса
Урок 14. Объём усечённого конуса
Урок 15. Объём шара и его частей
Урок 17. Комбинации тел (2)
Урок 18. Правильные многогранники
Урок 19. Объёмы подобных тел

Источник

Телом вращения называют пространственную фигуру, полученную в результате вращения некоторой плоской фигуры вокруг оси. Среди всех тел вращения выделяют цилиндр, конус и шар.

Цилиндром называют фигуру, полученную в результате вращения прямоугольника вокруг одной из его сторон (оси цилиндра).

Образующей цилиндра называют отрезок, соединяющий точки окружностей оснований цилиндра, и перпендикулярный диаметрам его оснований.

Высотой цилиндра называют перпендикуляр, заключенный между основаниями цилиндра.

На рисунке 9.66 прямая – ось вращения; – высота, – образующая цилиндра, полученного вращением прямоугольника вокруг стороны . Основание цилиндра – круг радиуса . Прямоугольник – осевое сечение цилиндра.

Объем цилиндра высоты находят по формуле:

$LaTeX formula: V=S_{o.}cdot h$ . (9.15)

Площадь основания цилиндра ( – радиус основания) находят по формуле:

$LaTeX formula: S_{o.}=pi r ^2$ . (9.16)

Площадь поверхности цилиндра находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.17)

Площадь боковой поверхности цилиндра находят по формуле:

$LaTeX formula: S_{delta .}=2pi r l$ , (9.18)

где – радиус основания, – высота, – образующая цилиндра.

Конусом называют фигуру, полученную в результате вращения прямоугольного треугольника вокруг одного из катетов (оси конуса).

Образующей конуса называют отрезок, соединяющий вершину конуса с точкой окружности основания конуса.

Высотой конуса называют перпендикуляр, соединяющий вершину конуса с центром его основания.

На рисунке 9.67 прямая – ось вращения; – высота конуса, – образующая конуса, – осевое сечение конуса, полученного вращением прямоугольного треугольника вокруг катета .

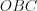
Усеченным конусом называют часть конуса, ограниченную его основанием и сечением, параллельным плоскости основания.

На рисунке 9.68 изображен усеченный конус.

Объем конуса высоты находят по формуле:

$LaTeX formula: V=frac{1}{3}S_{o.}cdot h$ . (9.19)

Площадь основания конуса ( – радиус основания) находят по формуле:

$LaTeX formula: S_{o.}=pi r^2$ . (9.20)

Площадь поверхности конуса находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.21)

Площадь боковой поверхности конуса находят по формуле:

$LaTeX formula: S_{delta .}=pi r l$ , (9.22)

где – радиус основания, – образующая конуса.

Объем усеченного конуса находят по формуле:

$LaTeX formula: V=frac{1}{3}pi h(r^2_1+r^2_2+r_1r_2)$ , (9.23)

где и – радиусы оснований, – высота.

Площадь боковой поверхности усеченного конуса находят по формуле:

$LaTeX formula: S_{delta .}=pi (r_1+r_2)l$ , (9.24)

где и – радиусы оснований, – высота, – образующая усеченного конуса.

Сферой называют фигуру, полученную в результате вращения полуокружности вокруг ее диаметра (рис. 9.69).

Шаром называют фигуру, полученную вращением полукруга вокруг его диаметра.

Сечение сферы плоскостью – окружность.

Сечение шара плоскостью – круг.

Сечение шара плоскостью, проходящей через центр шара, называют большим кругом (на рисунке 9.69 круг с центром в точке и радиусом ).

Касательной плоскостью к сфере (шару) называется плоскость, имеющая со сферой единственную общую точку (на рисунке 9.69 плоскость ). Эту точку называют точкой касания сферы и плоскости (на рисунке 9.69 точка ).

Касательная плоскость перпендикулярна радиусу сферы в точке касания.

Площадь сферы радиуса находят по формуле:

$LaTeX formula: S_{cphi .}=4pi R^2$ . (9.25)

Объем шара радиуса находят по формуле:

$LaTeX formula: V_{wapa}=frac{4}{3}pi R^3$ . (9.26)

Выпуклый многоугольник вписан в сферу, если все его вершины лежат на поверхности сферы, и описан около сферы, если все его стороны касаются поверхности сферы.

Сферическим (шаровым) сегментом называют часть сферы (шара), отсекаемую плоскостью.

Высотой шарового сегмента называют длину отрезка диаметра, перпендикулярного основанию шарового сегмента, расположенного между этим основанием и сферой (на рис. 9.70 ).

Шаровым сектором называют тело, полученное вращением кругового сектора вокруг одного из ограничивающих круговой сектор радиусов.

Высотой шарового сектора называют высоту части его сферической поверхности.

На рисунке 9.70 шаровой сектор получен в результате вращения кругового сектора вокруг радиуса .

Объем шарового сегмента находят по формуле:

$LaTeX formula: V_{c.}=pi h^2(R-frac{1}{3}h)$ . (9.27)

Площадь сферической поверхности находят по формуле:

$LaTeX formula: S_{n.}=2pi Rh$ , (9.28)

где – радиус шара; – высота сегмента.

Объем шарового сектора находят по формуле:

$LaTeX formula: V_{cekappa .}=frac{2}{3}pi R^2h$ , (9.29)

где – радиус шара; – высота сегмента.

Пример 1. Осевое сечение цилиндра – квадрат со стороной . Найдите объем и площадь поверхности цилиндра.

Решение. Так как осевое сечение квадрат (рис. 9.71), то , $LaTeX formula: r=frac{a}{2}$ .

По формулам 9.15 и 9.16 найдем объем цилиндра: $LaTeX formula: V=pi cdot frac{a^2}{4}cdot a=frac{pi a^3}{4}$ .

По формулам 9.16 , 9.17 и 9.18 найдем площадь поверхности цилиндра: $LaTeX formula: S_{n.}=frac{2pi a^2}{4}+frac{2pi a^2}{2}=frac{3pi a^2}{2}$ .

Ответ: ; .

Пример 2. Площадь боковой поверхности цилиндра равна , а объем его равен . Найдите высоту этого цилиндра.

Решение. Площадь боковой поверхности и объем цилиндра найдем по формулам 9.18 и 9.15 , где – радиус основания, – высота цилиндра.

Тогда согласно условию задачи запишем: $LaTeX formula: begin{cases} 2pi Rh=119, \ pi R^2h=7pi. end{cases}$

Разделим первое уравнение системы на второе и получим: $LaTeX formula: frac{2pi Rh}{pi R^2h}=frac{119}{7pi }$ , $LaTeX formula: frac{2}{R}=frac{17}{pi }$ , $LaTeX formula: R=frac{2pi }{17}$ .

Найдем из первого уравнения системы: $LaTeX formula: h=frac{119}{2pi R}=frac{119cdot 17}{2pi cdot 2pi }=frac{2023}{4pi ^2}$ .

Ответ: $LaTeX formula: frac{2023}{4pi ^2}$ .

Пример 3. Найдите объем и площадь поверхности конуса, осевым сечением которого является правильный треугольник со стороной см (рис. 9.72).

Решение. Так как см, а см, то из теоремы Пифагора: $LaTeX formula: h=sqrt{l^2-r^2}$ , (см).

По формулам 9.19 и 9.20 найдем объем конуса: $LaTeX formula: V=frac{1}{3}cdot pi cdot 3cdot 3=3pi$ ( $LaTeX formula: _{CM}\^3$ ).

По формулам 9.20 , 9.21 и 9.22 найдем площадь поверхности конуса: $LaTeX formula: S_{n.}=3pi +6pi =9pi$ ( $LaTeX formula: _{CM}\^2$ ).

Ответ: $LaTeX formula: _{CM}\^3$ ; $LaTeX formula: _{CM}\^2$ .

Пример 4. Радиус основания конуса равен , а угол при вершине в развертке его боковой поверхности равен $LaTeX formula: 90^{circ}$ . Определите объем конуса.

Решение. Рассмотрим конус радиуса и развертку его боковой поверхности – круговой сектор радиуса (рис. 9.73).

Найдем длину окружности в основании конуса: $LaTeX formula: C_{okappa p.}=2pi r=2sqrt{15}pi$ .

Найдем длину дуги в развертке боковой поверхности конуса: $LaTeX formula: C_{g.}=frac{2pi l}{360^{circ}}cdot 90^{circ}=frac{pi l}{2}$ .

Так как $LaTeX formula: C_{okappa p.}=C_{g.}$ , то $LaTeX formula: 2pi r=frac{pi l}{2}$ и .

Из теоремы Пифагора: , .

По формулам 9.19 и 9.20 найдем объем конуса: $LaTeX formula: V=frac{1}{3}cdot pi cdot 15cdot 15=75pi$ .

Ответ: .

Пример 5. Осевое сечение конуса – равнобокая трапеция с основаниями и . Образующая конуса равна . Найдите площадь боковой поверхности и объем конуса.

Решение. Имеем усеченный конус (рис. 9.74), радиусы оснований которого соответственно равны и . Зная образующую конуса , найдем его высоту: $LaTeX formula: h=sqrt{l^2-(r_1-r_2)^2}$ , .

По формуле 9.24 найдем площадь боковой поверхности конуса: $LaTeX formula: S_{delta .}=20sqrt{7}pi$ .

По формуле 9.23 найдем объем конуса:

$LaTeX formula: V=frac{1}{3}pi 2sqrt{7}(64+4+16)=56sqrt{7}pi$ .

Ответ: ; .

Пример 6. Периметр правильного шестиугольника, все вершины которого лежат на поверхности шара, равен . Объем шара равен . Найдите расстояние от центра шара до плоскости шестиугольника.

Решение. Найдем сторону правильного шестиугольника, зная его периметр: . Так как радиус окружности, описанной около правильного шестиугольника, равен его стороне, то на рисунке 9.75 .

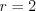
Объем шара находят по формуле 9.26 .

Так как , то $LaTeX formula: 36pi =frac{4}{3}pi R^3$ , $LaTeX formula: 9=frac{1}{3}R^3$ , , .

Из теоремы Пифагора: $LaTeX formula: d=sqrt{R^2-r^2}$ , .

Ответ: .

Пример 7. Сторона квадрата, описанного около шара, равна . Найдите площадь сферической поверхности, отсекаемой плоскостью квадрата от шара, если радиус шара равен (рис. 9.76).

Решение. 1. Найдем диагональ квадрата, зная его сторону: , . Поскольку сечение шара плоскостью – круг, а квадрат описан около этого круга, то радиус сечения равен: $LaTeX formula: r=frac{d}{2}$ , .

2. Из теоремы Пифагора: $LaTeX formula: l=sqrt{R^2-r^2}$ , .

3. Найдем высоту сферической поверхности:

, .

4. По формуле 9.28 найдем площадь сферической поверхности:

$LaTeX formula: S_{n.}=2pi Rh$ , $LaTeX formula: S_{n.}=10pi (5-sqrt{17})$ .

Ответ: .

Пример 8. Равнобедренная трапеция с основаниями см и см и острым углом $LaTeX formula: 60^{circ}$ вращается вокруг меньшего основания. Вычислите поверхность полученной фигуры вращения.

Решение. Рассмотрим равнобедренную трапецию с основаниями см и см (рис. 9.77). Вращая трапецию вокруг основания , получим тело, боковая поверхность которого состоит из боковой поверхности цилиндра и боковой поверхности двух равных конусов: $LaTeX formula: S_{n.}=S_{delta .}+2S_{delta .kappa .}$ . В трапеции из вершин и проведем высоты и . Тогда $LaTeX formula: BN=CM=R_{v.}=R_{kappa .}=h_{mp.}$ .

Рассмотрим прямоугольный треугольник : $LaTeX formula: angle BAN=60^{circ}$ , $LaTeX formula: AN=frac{1}{2}(AD-NM)=frac{1}{2}cdot 1=frac{1}{2}$ (см),

тогда (см) и $LaTeX formula: BN=sqrt{1^2-left ( frac{1}{2} right )^2}=frac{sqrt{3}}{2}$ (см).

Согласно формуле $LaTeX formula: S_{delta .v.}=2pi R_{v.}l_{v.}$ получим: $LaTeX formula: S_{delta .v.}=2pi cdot frac{sqrt{3}}{2}cdot 13=13sqrt{3}pi$ ( $LaTeX formula: _{CM}\^2$ ).

Согласно формуле $LaTeX formula: S_{delta .kappa .}=pi R_{kappa .}l_{kappa .}$ получим: $LaTeX formula: S_{delta .kappa .}=pi frac{sqrt{3}}{2}cdot 1=frac{sqrt{3}pi }{2}$ ( $LaTeX formula: _{CM}\^2$ ).

Найдем площадь поверхности тела вращения: $LaTeX formula: S_{n.}=13sqrt{3}pi +2cdot frac{sqrt{3}pi }{2}=14sqrt{3}pi$ ( $LaTeX formula: _{CM}\^2$ ).

Ответ: $LaTeX formula: _{CM}\^2$ .

1. В цилиндре умейте определять: радиус основания, высоту, образующую, осевое сечение.

2. В конусе умейте определять: радиус основания, высоту, образующую, осевое сечение.

3. Различайте шар и сферу (поверхность шара). Умейте определять: 1) центр, радиус и диаметр сферы; 2) в шаре: центр, радиус, диаметр, сечение, шаровой сегмент и шаровой сектор.

Источник

Тела вращения (объемные геометрические фигуры) : определения, формулы периметра поверхности и площади. Виды: цилиндр, конус, шар, шаровой сектор, шаровой сегмент.

Цилиндр

Цилиндр — тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями.
Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых (образующих) и проходящими через точки некоторой кривой (направляющей).
Основания цилиндра — плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями, ограничивающими цилиндр.
Высота цилиндра — расстояние между основаниями цилиндра.

Виды цилиндров

Прямой — цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), прямая между которыми перпендикулярна плоскостям этих оснований. Данная прямая называется осью цилиндра.
Косой — цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), отрезок между которыми не перпендикулярен плоскостям этих оснований.
Круговой — цилиндр с окружностью в роли направляющей.
Цилиндр вращения (или прямой круговой) — цилиндр, который можно получить вращением (то есть тело вращения) прямоугольника вокруг одной из его сторон, содержащая которую прямая в таком случае будет осью этого цилиндра и его осью симметрии.
Эллиптический, параболический и гиперболический – цилиндр, основания которого являются эллипсами, параболами или гиперболами. Последние два имеют бесконечный объём.
Равносторонний — цилиндр вращения, диаметр основания которого равен его высоте.

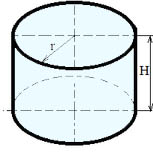
Формулы для цилиндра:

Объем цилиндра: V=π∙R²∙h или V=S_o∙h
Поверхность цилиндра: S= 2∙S_o + S_бок или S= 2∙π∙R² + 2∙π∙R∙h
Площадь основания: S_o= 2∙π∙R²Площадь боковой поверхности: S_бок=2∙π∙R∙h
Где: V — объем цилиндра, R — радиус цилиндра, h — высота цилиндра, S_o — площадь основания цилиндра, π = 3.141592.

Формулы для полого цилиндра:

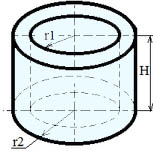
Объем цилиндра: V = π ∙ h ∙ (r₂² — r₁²) где r₂ > r₁Площадь боковой поверхности: S_бок = 2 ∙ π ∙ h ∙ (r₁ + r₂)
Где: V — объем цилиндра, R — радиус цилиндра, h — высота цилиндра, S_o — площадь основания цилиндра, π = 3.141592.

Конус

Конус – поверхность, образованная в пространстве множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса).
Боковая поверхность конуса — объединение образующих конуса; образующая поверхность конуса является конической поверхностью.
Высота конуса — отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка).
Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
Конусность — соотношение высоты и диаметра основания конуса.

Типы конусов

Прямой — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром. Прямая, соединяющая вершину и центр основания, называется осью конуса.
Косой (или наклонный) — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
Круговой — конус, основание которого является кругом.
Конус вращения или прямой круговой конус (часто под конусом подразумевают именно его) — конус, который можно получить вращением (то есть тело вращения) прямоугольного треугольника вокруг прямой, содержащей катет треугольника (эта прямая является осью конуса).
Эллиптический, параболический и гиперболический — конус, опирающийся на эллипс, параболу или гиперболу. Последние два имеют бесконечный объем.
Усечённый или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.
Равносторонний — конус вращения, образующая которого равна диаметру основания.

Формулы для конуса:

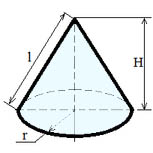
Объем конуса: V = 1/3·π·R²·h или V=1/3·S_o·h
Поверхность конуса: S=S_o+S_бок или S=π∙R²+π∙R∙h
Площадь основания: S_o=π∙R²Площадь боковой поверхности: S_бок=π∙R∙l
Образующая: l=√(R²+h²)
Где: V — объем конуса, S_o — площадь основания, R — радиус основания, h — высота конуса, l — образующая, π=3.141592.

Формулы для усеченного конуса:

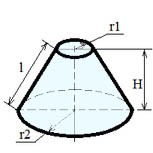
Объем конуса: V=1/3·π·(r₁²+r₂²+r₁·r₂)·h
Площадь боковой поверхности: S_бок=π∙(r₁+r₂)∙l
Где: r1 — радиус нижнего основания усеченного конуса; r2 — радиус верхнего основания усеченного конуса; l — образующая усеченного конуса, π=3.141592.

Шар

Шар — это тело ограниченное шаровой поверхностью.
Шаровая (сферическая) поверхность – это геометрическое место точек пространства, равноудаленных от одной точки — центра шара. Радиус и диаметр определяют также, как и для окружности.
Все плоские сечения шара — круги. Наибольший круг получается в сечении шара плоскостью, проходящей через центр. Такой круг делит шар пополам. Радиус большого круга равен радиусу шара. Через две точки шара, лежащие на концах одного диаметра, можно провести бесчисленное множество больших кругов — меридианы. Через две точки, не лежащие на концах диаметра шара можно провести только один большой круг.
Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью основанием которой служит основание сегмента, а вершиной — центр шара.
Шаровой (сферический) сегмент — часть шара, осекаемая от него какой-нибудь плоскостью. Основание шарового сегмента – круг. Высота шарового сегмента — длина перпендикуляра от поверхности шара до основания. Вершина шарового сегмента — точка пересечения высоты шарового сегмента с поверхностью шара.
Шаровой слой — это часть шара, заключенная между двумя секущими параллельными плоскостями. Шаровой пояс или Шаровая зона — кривая поверхность шарового слоя. Круги — основания шарового пояса. Расстояние между основаниями — высота шарового слоя.

Формулы для шара:

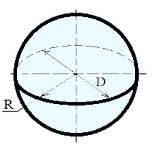
Объем шара: V = 4/3 ·π· R³ или V=1/6 ·π · D³
Площадь поверхности сферы: S= 4 ·π· R² или S=π · D²
Площадь основания: S_o=π∙R²Где: R — радиус шара, π = 3.141592.

Формулы для шарового сектора:

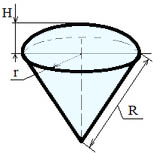
Высота конуса: h_конуса=R²−r²
Высота сегмента: h_{сегмента}= R−R²−r²Площадь поверхности шарового сектора: S_{сектора}= S_{сегмента}+ S_конуса
или S_{сектора}= 2∙π∙R∙h_{сегмента}+ π∙R∙rили S_{сектора}=2∙π∙ R ∙(R−R²−r²) + π∙R∙r
Объем шарового сектора: V = 2/3∙(π∙R²∙h) или V = 1/3∙( R∙S)
Где: R — радиус шара, r — радиус сегмента, π = 3.141592.

Формулы для шарового сегмента:

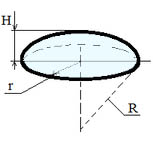
Площадь поверхности шарового сегмента : S = 2∙π∙R∙h
Объем шарового сегмента : V = (π ·H² (R -1/3 ·h)
Где: R — радиус шара, r — радиус сегмента, h= высота шарового сегмента, π = 3.141592.

Также на сайте описаны многогранники, в том числе: определения и формулы.

Источник

Тела и поверхности вращения. Шар. Цилиндр. Конус

Шар

Площадь поверхности сферы

Объем шара

Цилиндр

Площадь боковой поверхности цилиндра

Площадь полной поверхности цилиндра

Объем цилиндра

Конус

Площадь поверхности конуса

Объём конуса

Бонус: Вебинары по стереометрии из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 14 Стереометрия. Расстояние между точками и от точки до прямой

ЕГЭ 14. Стереометрия. Пирамида. Разбор варианта профильного ЕГЭ 2020

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Слайд 1Площадь поверхности тел вращения

Слайд 2Основная цель: сформиравать навык решения задач по

теме

Слайд 3 Тело, полученное вращением прямоугольного треугольника вокруг прямой,

содержащей гипотенузуВозьмем прямоугольный треугольникВращение будет производиться вокруг

Слайд 4Тело, полученное вращением прямоугольного треугольника вокруг прямой,

проходящей через вершину острого угла, параллельно противоположному

Слайд 5

C

Слайд 6 Тело, полученное вращением равностороннего треугольника вокруг прямой,

содержащей одну из сторон треугольника

Слайд 7 Тело, полученное вращением тупоугольного равнобедренного треугольника вокруг

прямой, содержащей основание треугольника

Слайд 8 Тело, полученное вращением равностороннего треугольника вокруг прямой,

проходящей через вершину треугольника параллельно противолежащей стороне

Слайд 9 Тело, полученное вращением прямоугольного треугольника вокруг прямой,

проходящей через вершину острого угла перпендикулярно гипотенузе

Слайд 10 Тело, полученное вращением прямоугольной трапеции вокруг прямой,

содержащей меньшую боковую сторону

Слайд 11 Тело, полученное вращением прямоугольной трапеции вокруг прямой,

содержащей меньшее основание

Слайд 12 Тело, полученное вращением прямоугольной трапеции вокруг прямой,

содержащей большее основание

Слайд 13 Тело, полученное вращением равнобедренной трапеции вокруг прямой,

содержащей меньшее основание

Слайд 14 Тело, полученное вращением равнобедренной трапеции вокруг прямой,

содержащей большее основание

Слайд 15 Тело, полученное вращением ромба вокруг прямой, содержащей

сторону ромба

Слайд 16 Тело, полученное вращением ромба вокруг прямой, проходящей

через вершину ромба параллельно одной из диагоналей.

Слайд 17Задача 1 Прямоугольный треугольник с катетом 8

см и прилежащим к нему углом 30°

Слайд 18Задача 2 Равнобедренный треугольник, у которого боковые

стороны равны по 4 см, а один

Слайд 20Задача В равнобедренной трапеции основания равны 14

и 50 см, а диагональ 40 см.

Цилиндр

Конус

Шар

Слайд 1Площадь поверхности
тел вращения

Слайд 2Основная цель:
сформиравать навык решения задач по

Слайд 3

Тело, полученное вращением прямоугольного треугольника вокруг прямой,

содержащей гипотенузу
Возьмем прямоугольный треугольник
Вращение будет производиться вокруг

Слайд 6

Тело, полученное вращением равностороннего треугольника вокруг прямой,

Слайд 7

Тело, полученное вращением тупоугольного равнобедренного треугольника вокруг

Слайд 8

Тело, полученное вращением равностороннего треугольника вокруг прямой,

Слайд 9

Тело, полученное вращением прямоугольного треугольника вокруг прямой,

Слайд 10

Тело, полученное вращением прямоугольной трапеции вокруг прямой,

Слайд 11

Тело, полученное вращением прямоугольной трапеции вокруг прямой,

Слайд 12

Тело, полученное вращением прямоугольной трапеции вокруг прямой,

Слайд 13

Тело, полученное вращением равнобедренной трапеции вокруг прямой,

Слайд 14

Тело, полученное вращением равнобедренной трапеции вокруг прямой,

Слайд 15

Тело, полученное вращением ромба вокруг прямой, содержащей

Слайд 16

Тело, полученное вращением ромба вокруг прямой, проходящей

Слайд 17Задача 1
Прямоугольный треугольник с катетом 8

Слайд 18Задача 2
Равнобедренный треугольник, у которого боковые

Слайд 20Задача
В равнобедренной трапеции основания равны 14