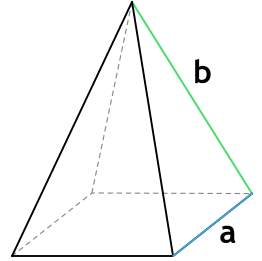
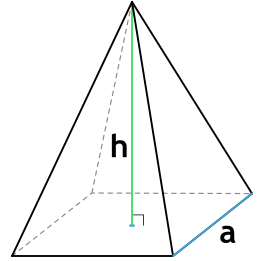
1. Многогранник и шар
Шар вписан в призму, если он касается всех граней призмы.
Шар описан около призмы, если все вершины призмы лежат на поверхности шара.
Не во всякую призму можно вписать шар и не около всякой призмы можно описать шар.
Шар вписан в пирамиду, если он касается всех граней пирамиды.
Шар описан около пирамиды, если все вершины пирамиды лежат на поверхности шара.
2. Многогранник и цилиндр
Цилиндр вписан в прямую призму, если основания цилиндра вписаны в основания призмы.
Цилиндр описан около прямой призмы, если его основания описаны около оснований призмы.
Цилиндр вписан в пирамиду, если одно из его оснований принадлежит основанию пирамиды, а другое его основание вписано в сечение пирамиды плоскостью, параллельной ее основанию.
Цилиндр описан около пирамиды, если основание пирамиды вписано в одно из оснований цилиндра, а вершина пирамиды принадлежит другому основанию цилиндра.
3. Многогранник и конус
Конус вписан в призму, если основание конуса вписано в одно из оснований призмы, а вершина конуса принадлежит другому основанию призмы.
Конус описан около призмы, если вершины одного из оснований призмы лежат на поверхности конуса, а все вершины другого основания призмы принадлежат основанию конуса.
Конус вписан в пирамиду, если основание конуса вписано в основание пирамиды, а вершина конуса совпадает с вершиной пирамиды.
Конус описан около пирамиды, если основание конуса описано около основания пирамиды, а вершина конуса совпадает с вершиной пирамиды.
4. Комбинация тел вращения
Шар вписан в конус, если он касается основания конуса в его центре, а боковой поверхности – по окружности. Центр шара находится на оси конуса и равноудален от центра основания и образующей конуса.
Шар описан около конуса, если вершина и окружность основания конуса лежат на поверхности шара. Центр шара лежит на прямой, содержащей ось конуса, и равноудален от вершины и точек окружности основания конуса.
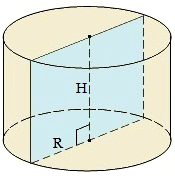
Шар вписан в цилиндр, если он касается оснований цилиндра в их центрах, а боковой поверхности цилиндра по большой окружности шара, параллельной основаниям. Центр шара лежит на середине оси цилиндра, а радиус шара можно найти по формуле:


Шар описан около цилиндра, если окружности оснований цилиндра лежат на поверхности шара.
Не во всякий цилиндр можно вписать шар, но около всякого цилиндра можно описать шар.
При решении задач целесообразно строить вспомогательное сечение, проходящее через ось цилиндра или конуса и центр шара. При этом в сечении цилиндра будет получаться прямоугольник, в сечении конуса – равнобедренный треугольник, в сечении шара – круг с радиусом, равным радиусу шара.
Конус вписан в цилиндр, если основание конуса совпадает с одним из оснований цилиндра, а вершина конуса совпадает с центром другого основания цилиндра.
Конус описан около цилиндра, если одно из оснований цилиндра касается боковой поверхности конуса, а другое основание цилиндра принадлежит основанию конуса.
Пример 1. Шар радиуса 
Решение. Шар можем вписать только в прямоугольный параллелепипед, основание которого является квадрат (рис.9.78). Следовательно, имеем куб с ребром 


Найдем радиус шара, описанного около куба: 
По формуле 9.26 найдем объем шара, описанного около куба: 
Ответ: 
Пример 2. Все вершины треугольной призмы, основанием которой является треугольник со сторонами 



Решение. Так как шар описан около призмы, то все вершины призмы лежат на поверхности шара. Центр шара, с одной стороны, равноудален от вершин призмы, а с другой стороны, равноудален от центров окружностей, описанных около оснований призмы.
На рисунке 9.79: точки 




Радиус окружности, описанной около основания призмы, найдем по формуле 
Площадь основания призмы найдем по формуле Герона 

Тогда 
По теореме Пифагора: 

Площадь поверхности шара найдем по формуле 9.25 : 
Ответ: 
Пример 3. Найдите отношение радиуса шара, описанного около правильного тетраэдра, к радиусу шара, вписанного в этот тетраэдр.
Решение. Пусть ребро тетраэдра равно 





Поскольку точки 




Угол 



Вписанный шар касается всех граней тетраэдра, следовательно, его радиус является перпендикуляром к плоскостям граней, то есть 
Так как 





Длину отрезка 

Найдем отношение радиусов описного около тетраэдра и вписанного в тетраэдр шаров:

Ответ: 
Пример 4. В прямой параллелепипед, одна из диагоналей оснований которого равна 

Решение. Окружность можно вписать в квадрат или в ромб. Но диагональ квадрата не может быть равна его стороне. Диагональ ромба может быть равна его стороне, если угол ромба равен 
Согласно формуле 

Высота параллелепипеда равна высоте цилиндра: 
Согласно формуле 9.6 найдем объем параллелепипеда:

Ответ: 
Пример 5. Около правильной треугольной пирамиды описан цилиндр, объем которого равен 
Решение. Пусть 

Согласно формулам 9.15 и 9.16 запишем: 

Так как основание пирамиды – правильный треугольник со стороной 


Найдем площадь основания пирамиды: 
Согласно формуле 9.11 запишем объем пирамиды: 


Ответ: 
Пример 6. Конус вписан в треугольную призму, основанием которой является прямоугольный треугольник с катетами 


Решение. 1. Найдем гипотенузу треугольника: 
2. Найдем радиус окружности, вписанной в основание призмы:


3. Высота конуса равна высоте призмы: 
4. По теореме Пифагора найдем образующую конуса:


5. По формуле 9.22 найдем боковую поверхность конуса: 

Ответ: 
Пример 7. Правильная шестиугольная пирамида вписана в конус, объем которого равен 
Решение. На рисунке 9.82: 


С учетом формул 9.19 и 9.20 получим: 





Найдем радиус окружности, вписанной в шестиугольник: 

По теореме Пифагора найдем апофему пирамиды:

По формуле 9.13 найдем площадь боковой поверхности пирамиды:


Ответ: 
Пример 8. Конус, высота которого равна 

Решение. На рисунке 9.83 построено осевое сечение конуса. Так как 


По теореме Пифагора: 

Ответ: 
Пример 9. В конус, осевое сечение которого – равносторонний треугольник, вписан шар. Найдите объем конуса, если объем шара равен 

Решение. Объем шара находят по формуле 9.26 . Радиус шара найдем, решая уравнение 






В свою очередь радиус окружности, вписанной в правильный треугольник со стороной 



Найдем радиус основания конуса и его высоту: 


Согласно формулам 9.19 и 9.20 найдем объем конуса: 

Ответ: 
Пример 10. В цилиндр, площадь поверхности которого равна 
Решение. Осевое сечение цилиндра – квадрат. Тогда, если радиус основания цилиндра 


Согласно условию задачи: 





Тогда 

Ответ: 
1. В любую треугольную пирамиду можно вписать шар и около любой треугольной пирамиды можно описать шар.
2. В любой конус можно вписать шар и около любого конуса можно описать шар.
3. Решая задачи стереометрии, часто вовсе не обязательно изображать сами пространственные фигуры, а достаточно лишь выполнить некоторые фрагменты рисунка.
Объем прямой призмы высоты 


Площадь поверхности прямой призмы находят по формуле:

Площадь боковой поверхности прямой призмы высоты 


Объем наклонной призмы можно вычислить по формуле:

Площадь поверхности наклонной призмы можно вычислить по формуле:

Объем пирамиды высоты 

Площадь поверхности пирамиды находят по формуле:

Площадь боковой поверхности правильной пирамиды находят по формуле:

где 
Объем цилиндра высоты 

Площадь основания цилиндра (

Площадь поверхности цилиндра находят по формуле:

Площадь боковой поверхности цилиндра находят по формуле:

где 


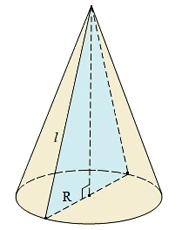
Объем конуса высоты 

Площадь основания конуса (

Площадь поверхности конуса находят по формуле:

Площадь боковой поверхности конуса находят по формуле:

где r – радиус основания, l – образующая конуса.
Площадь сферы радиуса 

Объем шара радиуса

Площадь поверхности геометрической фигуры измеряется в квадратных единицах. Очень часто используется в повседневной жизни, в строительстве, на производствах. Например, нужно вам покрасить комнату, зная сколько краски используется на кв. метр, и площади стен комнаты легко можно вычислить, сколько всего вам нужно купить краски.
Различают два вида площадей поверхности тел: Sбок — площадь боковой поверхности тела, и Р — площадь полной поверхности тела, которая равна сумме площадей боковой поверхности и основания тела.
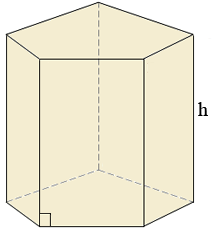
Формула площади поверхности призмы
Площадь боковой поверхности прямой призмы равна периметру основания умноженному на высоту призмы (высота=боковому ребру).
Sбок = ph=pl
р — периметр основания;
h — высота;
l — боковое ребро.
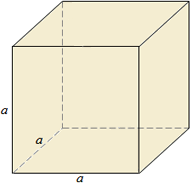
Формула площади поверхности куба
Площадь боковой поверхности куба равна числу боковых граней умноженному на квадрат ребра.
Sбок = 4a2
Площадь полной поверхности куба равна числу всех граней куба умноженному на квадрат ребра.
P = 6a2
а — ребро куба.
Формула площади поверхности пирамиды
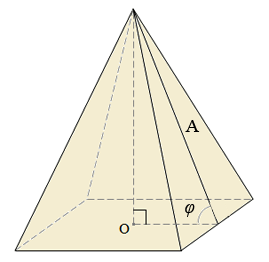
1) Правильная пирамида:
Sбок = pA
p — периметр основания;
A — апофема.
Sбок =
S — площадь основания;
φ — угол между боковой гранью и основанием пирамиды.
Sбок = Sгр n
Sгр — площадь одной боковой грани; n — количество боковых граней пирамиды.
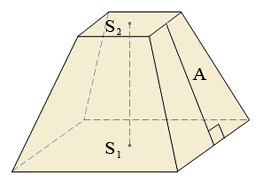
2) Правильная усеченная пирамида:
Sбок = (p1+p2)A
p1 ,p2 — периметры оснований;
A — апофема.
Р = Sбок + S1 + S2
Р — площадь полной поверхности правильной усеченной пирамиды;
Sбок — площадь боковой поверхности правильной усеченной пирамиды;
S1 + S2 — площади оснований.
Формула площади поверхности цилиндра
Sбок = 2rh =
dh
P = 2r2+2
rh = 2
(r+h)
P — площадь полной поверхности цилиндра;
r — радиус цилиндра;
d — диаметр цилиндра;
h — высота цилиндра.
Формула площади поверхности конуса
1) Прямой круговой конус:
Sбок = rl = 1/2
dl
P = r2 +
rl=
r(r+l)
P — площадь полной поверхности конуса;
r -радиус конуса;
d -диаметр конуса;
l — образующая конуса.
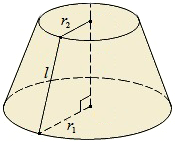
2) Усеченный прямой круговой конус:
Sбок = l(r1 + r2) = 1/2
l(d1 + d2)
P = l(r1 + r2) +
(r1 + r2)
P — площадь полной поверхности усеченного конуса;
r1, r2 — радиусы оснований усеченного конуса;
d1, d2 — диаметры оснований усеченного конуса;
l — образующая усеченного конуса.
Формула площади поверхности шара (сферы)
Шар — тело, созданное вращением полукруга вокруг диаметра.
Сфера — поверхность шара.
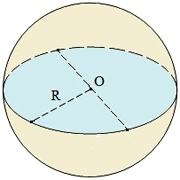
P = 4R2 =
D2
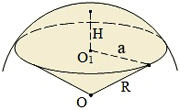
Формула площади поверхности сферического сегмента
Сферический сегмент — часть сферы, что отсекается от сферы плоскостью.
Sсф. сегм. = 2Rh =
(a2 + h2)
Формула площади поверхности шарового сегмента
Шаровой сегмент — часть шара, что отсекается от шара плоскостью, и ограничивается кругом (основание шарового сегмента) и сферическим сегментом.
Sшар. сегм. = (2Rh+a2) =
(h2+2a2)
R — радиус шара;
D — диаметр шара;
h — высота сегмента;
a — радиус основания сегмента
Площадь полной поверхности куба равна 1,5 м2. Найдите ребро куба.
Найти площадь боковой поверхности конуса с радиусом равным 3 см, образованным направляющей равной 7 см.
Радиус большего основания, образующая и высота усеченного конуса равны 7, 5 и 4 см соответственно. Найдите площадь боковой поверхности конуса.

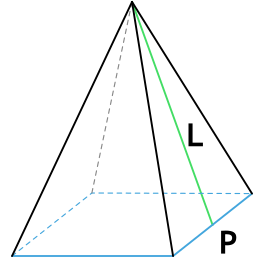
{S_{полн} = dfrac{1}{2}PL + S}
На странице вы найдете онлайн-калькуляторы, которые помогут найти площадь полной и боковой поверхности правильной пирамиды, а также треугольной, четырехугольной и шестиугольной пирамиды. Кроме того приводятся формулы, по которым вы можете произвести расчет самостоятельно.
- калькулятор площади поверхности пирамиды
- формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
- формула площади полной поверхности правильной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и боковую грань
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной пирамиды через периметр и апофему
- формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- примеры задач
Познакомьтесь с важными понятиями, которые необходимо знать для расчета площади поверхности пирамиды.
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.
Площадь полной поверхности пирамиды — это сумма площадей боковых граней и площади основания.
Площадь боковой поверхности пирамиды — это совокупная площадь всех боковых граней пирамиды.
Апофема — перпендикуляр, опущенный из вершины пирамиды на ребро основания.
Формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
{S_{полн} = dfrac{1}{2}PL+S}
P — периметр основания пирамиды
L — апофема пирамиды
S — площадь основания пирамиды
Формула площади полной поверхности правильной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{na}{2} {Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} + sqrt{h^2+ Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
n — число сторон основания
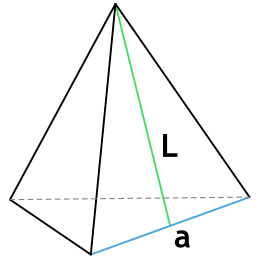
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{a^2 sqrt{3}+6aL}{4}}
a — сторона основания пирамиды
L — апофема пирамиды
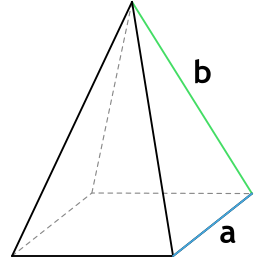
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{a^2 sqrt{3}+6a sqrt{b^2 — dfrac{a^2}{4}}}{4}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{3a}{2} {Bigg( dfrac{a}{2 tg ( 60°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{полн} = 2a {Bigg( dfrac{a}{2 tg ( 45°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{полн} = a^2+2aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3aL}
a — сторона основания пирамиды
L — апофема пирамиды
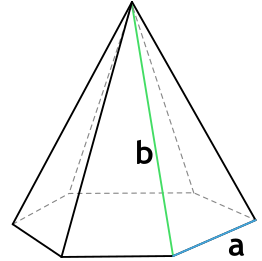
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3asqrt{b^2-dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{полн} = 3a {Bigg( dfrac{a}{2 tg ( 30°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной пирамиды через периметр и апофему
{S_{бок} = dfrac{1}{2}PL}
P — периметр основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{na}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( dfrac{180°}{n})} Bigg) ^2} }
a — сторона основания пирамиды
h — высота пирамиды
n — число сторон основания
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{бок} = dfrac{3}{2}aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{бок} = dfrac{3a sqrt{b^2 — dfrac{a^2}{4}}}{2}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{3a}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
{S_{бок} =dfrac{1}{2}PL}
P — периметр основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{бок} = 2aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 2a sqrt{b^2 — dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{бок} = 3aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 3asqrt{b^2-dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{бок} = 3a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Примеры задач на нахождение площади поверхности пирамиды
Задача 1
Стороны основания правильной четырехугольной пирамиды равны 60см, боковые ребра равны 78см. Найдите площадь поверхности этой пирамиды.
Решение
Так как пирамида правильная четырехугольная, то воспользуемся соответствующей формулой площади поверхности через сторону основания и боковую грань.
S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}} = 60^2 + 2 cdot 60 sqrt{78^2- dfrac{60^2}{4}} = 3600 + 120 sqrt{6084- dfrac{3600}{4}} = 3600 + 120 sqrt{6084 — 900} = 3600 + 120 sqrt{5184} = 3600 + 120 cdot 72 = 3600 + 8640 = 12240 : см²
Ответ: 12240 см²
Проверим полученный ответ с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной треугольной пирамиды со стороной 6см и апофемой 10см.
Решение
Из условия мы знаем апофему и сторону правильной треугольной пирамиды, поэтому нам потребуется эта формула.
S_{бок} = dfrac{3}{2}aL = dfrac{3}{2} cdot 6 cdot 10 = dfrac{3}{2} cdot 60 = 90 : см²
Ответ: 90 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной четырехугольной пирамиды сторона основания 6см и высота 4см.
Решение
Подставим значения в формулу и произведем расчет.
S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} = 2 cdot 6 sqrt{4^2+ Bigg( dfrac{6}{2 tg ( 45°)} Bigg) ^2} = 60 : см²
Ответ: 60 см²
Проверка .
Формулы объёма и площади поверхности. Многогранники.
Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:
- Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
- Элементарная логика.
Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.
 Куб |
|
|
 Параллелепипед |
|
|
 Прямоугольный параллелепипед |
|
|
 Призма |
|

|
 Пирамида |
|

|
Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».
Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.
Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.
Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.
Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.
Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение:
Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 
Очевидно, их 6, поскольку у куба 6 граней.
Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.
Разберем задачи, где требуется найти площадь поверхности многогранника.
Мы рассмотрим призмы и пирамиды. Начнем с призмы.
Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.
Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Многогранник на рисунке – это прямая призма с высотой 12.
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
(больший квадрат),
(маленький прямоугольник),
Подставим все данные в формулу: 
Ответ: 424.
Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение.
Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:
Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:
(большой прямоугольник),
(маленький прямоугольник).
Найдем площадь полной поверхности:
Ответ: 54
Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Покажем еще один способ решения задачи.
Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.
И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:
Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.
Ответ: 42
Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.
Решение.
Пусть АВ = 5 см, ВС = 3 см, тогда
Из по теореме косинусов найдем ребро АС:
Отрезок АС – большая сторона , следовательно,
большая боковая грань призмы.
Поэтому или
откуда
Ответ: 75
Теперь две задачи на площадь боковой поверхности пирамиды.
Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.
Решение.
Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.
Проведем , тогда
(по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.
– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.
Из прямоугольного получим:
Из прямоугольного имеем:
(по двум катетам), тогда
следовательно
Ответ: 192
Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.
Решение:
Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.
Площадь поверхности пирамиды равна
где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.
Значит, полупериметр основания .
Апофему найдем по теореме Пифагора:
Ответ: 2256
Как решать задачи на нахождение объема многогранника сложной формы?
Покажем два способа.
Первый способ
1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.
Второй способ.
1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.
Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
1) Достроим составной многогранник до параллелепипеда.
2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:
3) Найдем объем лишней части, то есть маленького параллелепипеда.
Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем
4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
Ответ: 220.
Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.
Объем призмы равен , а так как призма прямая, то ее боковое ребро является и высотой, то есть
Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания
Ответ: 126
Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.
Решение.
Объем призмы равен
Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.
Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.
Объем воды не изменился, Так как
высота воды
должна быть в 81 раз меньше, чем
Она равна
(см).
Ответ: 4
Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды
Решение.
Опустим из вершины высоту
Н на основание
Диагональ основания делит его на два равных треугольника, следовательно,
Имеем:
Ответ: 3,5
Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна
Решение.
По формуле объема пирамиды, 
В основании пирамиды лежит правильный треугольник. Его площадь равна
Объем пирамиды
Ответ: 96
Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.
Решение.
По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.
Пусть тогда
Так как точки М и К – середины АD и DС соответственно, то
Площадь треугольника MDK, лежащего в основании новой призмы, составляет часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен
Ответ: 4
Докажем полезную теорему.
Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство:
Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.
Больше задач на формулы объема и площади поверхности здесь.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
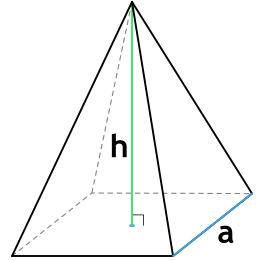
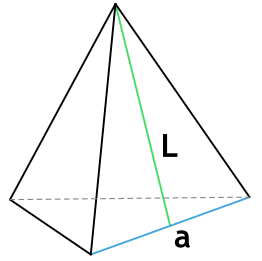
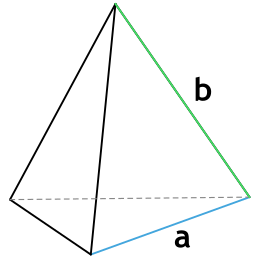
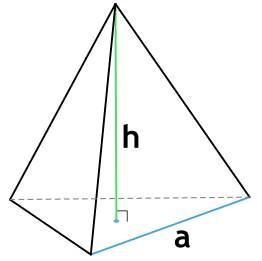
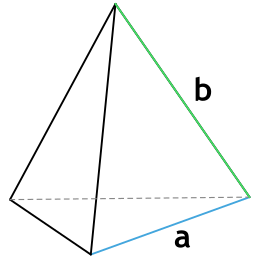
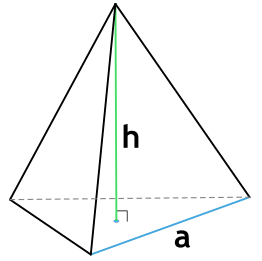
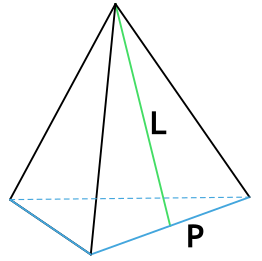
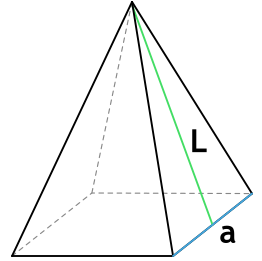
Площадь поверхности пирамиды. В этой статье мы рассмотрим с вами задачи с правильными пирамидами. Напомню, что правильная пирамида – это пирамида, основанием которой является правильный многоугольник, вершина пирамиды проецируется в центр этого многоугольника.
Боковая грань такой пирамиды это равнобедренный треугольник. Высота этого треугольника, проведенная из вершины правильной пирамиды, называется апофемой, SF – апофема:
В представленном ниже типе задач требуется найти площадь поверхности всей пирамиды или площадь её боковой поверхности. На блоге уже рассмотрено несколько задач с правильными пирамидами, где ставился вопрос о нахождении элементов (высоты, ребра основания, бокового ребра), можете посмотреть.
В типовых заданиях, как правило, рассматриваются правильные треугольные, четырёхугольные и шестиугольные пирамиды. Задач с правильными пятиугольными и семиугольными пирамидами пока не встречал.
Кстати, на проекте youclever неплохой визуальный гид по пирамиде: с красивыми картинками, основными формулами и свойствами. Подходит тем, кто лучше воспринимает информацию визуально. Там весь учебник по геометрии такой — мало задач, но много понятных рисунков.
Формула площади всей поверхности проста — требуется найти сумму площади основания пирамиды и площади её боковой поверхности:
Рассмотрим задачи:
Стороны основания правильной четырехугольной пирамиды равны 72, боковые ребра равны 164. Найдите площадь поверхности этой пирамиды.
Площадь поверхности пирамиды равна сумме площадей боковой поверхности и основания:
*Боковая поверхность состоит из четырёх равных по площади треугольников. Основание пирамиды это квадрат.
Площадь боковой стороны пирамиды можем вычислить воспользовавшись формулой Герона:
Таким образом, площадь поверхности пирамиды равна:
Ответ: 28224
Стороны основания правильной шестиугольной пирамиды равны 22, боковые ребра равны 61. Найдите площадь боковой поверхности этой пирамиды.
Основанием правильной шестиугольной пирамиды является правильный шестиугольник.
Площадь боковой поверхности данной пирамиды состоит из шести площадей равных треугольников с сторонами 61,61 и 22:
Найдём площадь треугольника, воспользуемся формулой Герона:
Таким образом, площадь боковой поверхности равна:
Ответ: 3240
*В представленных выше задачах площадь боковой грани можно было найти используя другую формулу треугольника, но для этого нужно вычислить апофему.
27155. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
Для того, чтобы найти площадь поверхности пирамиды нам необходимо знать площадь основания и площадь боковой поверхности:
Площадь основания равна 36, так как это квадрат со стороной 6.
Боковая поверхность состоит из четырёх граней, которые являются равными треугольниками. Для того, чтобы найти площадь такого треугольника требуется знать его основание и высоту (апофему):
*Площадь треугольника равна половине произведения основания и высоты проведённой к этому основанию.
Основание известно, оно равно шести. Найдём высоту. Рассмотрим прямоугольный треугольник (он выделен жёлтым):
Один катет равен 4, так как это высота пирамиды, другой равен 3, так как он равен половине ребра основания. Можем найти гипотенузу, по теореме Пифагора:
Значит площадь боковой поверхности пирамиды равна:
Таким образом, площадь поверхности всей пирамиды равна:
Ответ: 96
27069. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Посмотреть решение
27070. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Посмотреть решение
Существуют ещё формулы площади боковой поверхности правильной пирамиды. В правильной пирамиде основание является ортогональной проекцией боковой поверхности, поэтому:
где φ — двугранный угол при основании
Отсюда площадь полной поверхности правильной пирамиды может быть найдена по формуле:
Еще одна формула боковой поверхности правильной пирамиды:
P — периметр основания, l — апофема пирамиды
*Эта формула основывается на формуле площади треугольника.
Если хотите узнать подробнее как эти формулы выводятся, не пропустите, следите за публикацией статей. На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.