Как найти площадь правильного десятиугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Правильный десятиугольник

Площадь правильного десятиугольника — это число, характеризующее десятиугольник в единицах измерения площади.

Правильный десятиугольник (декагон) — это десятиугольник у которого все стороны и углы равны.

Содержание

1 Обозначения
2 Формулы:
- 2.1 n=10:
- 2.2 α=π/10:
3 Другие многоугольники:
4 Ссылки

Обозначения

Введём обозначения:

a — длина стороны;

n — число сторон, n=10;

r — радиус вписанной окружности;

R — радиус описанной окружности;

α — половинный центральный угол, α=π/10;

P₁₀ — периметр правильного десятиугольника;

S_Δ — площадь равнобедренного треугольника с основанием равным стороне и боковыми сторонами равными радиусу описанной окружности;

S₁₀ — площадь правильного десятиугольника.

Формулы:

n=10:

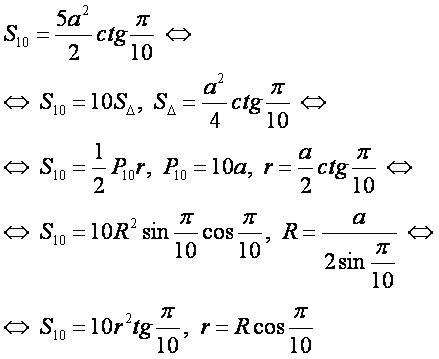
α=π/10:

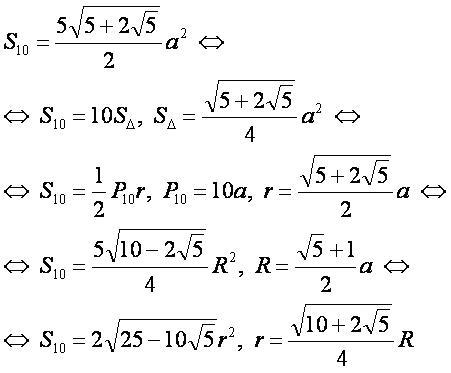
где

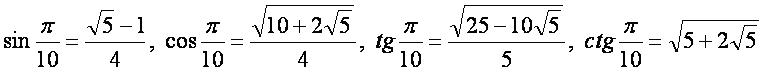
Другие многоугольники:

Ссылки

Участник:Logic-samara

Источник

From Wikipedia, the free encyclopedia

Regular decagon
A regular decagon
Type	Regular polygon
Edges and vertices	10
Schläfli symbol	{10}, t{5}
Coxeter–Dynkin diagrams
Symmetry group	Dihedral (D₁₀), order 2×10
Internal angle (degrees)	144°
Properties	Convex, cyclic, equilateral, isogonal, isotoxal
Dual polygon	Self

In geometry, a decagon (from the Greek δέκα déka and γωνία gonía, «ten angles») is a ten-sided polygon or 10-gon.^[1] The total sum of the interior angles of a simple decagon is 1440°.

Regular decagon[edit]

A regular decagon has all sides of equal length and each internal angle will always be equal to 144°.^[1] Its Schläfli symbol is {10} ^[2] and can also be constructed as a truncated pentagon, t{5}, a quasiregular decagon alternating two types of edges.

Side length[edit]

The picture shows a regular decagon with side length and radius of the circumscribed circle.

So the regular decagon can be constructed with ruler and compass.

Further conclusions

${displaystyle ;R={frac {2a}{{sqrt {5}}-1}}={frac {a}{2}}({sqrt {5}}+1);}$ and the base height of ${displaystyle Delta ,E_{10}E_{1}M,}$ (i.e. the length of ) is ${displaystyle h={sqrt {R^{2}-(a/2)^{2}}}={frac {a}{2}}{sqrt {5+2{sqrt {5}}}};}$ and the triangle has the area: ${displaystyle A_{Delta }={frac {a}{2}}cdot h={frac {a^{2}}{4}}{sqrt {5+2{sqrt {5}}}}}$ .

Area[edit]

The area of a regular decagon of side length a is given by:^[3]

${displaystyle A={frac {5}{2}}a^{2}cot left({frac {pi }{10}}right)={frac {5}{2}}a^{2}{sqrt {5+2{sqrt {5}}}}simeq 7.694208843,a^{2}}$

In terms of the apothem r (see also inscribed figure), the area is:

${displaystyle A=10tan left({frac {pi }{10}}right)r^{2}=2r^{2}{sqrt {5left(5-2{sqrt {5}}right)}}simeq 3.249196962,r^{2}}$

In terms of the circumradius R, the area is:

${displaystyle A=5sin left({frac {pi }{5}}right)R^{2}={frac {5}{2}}R^{2}{sqrt {frac {5-{sqrt {5}}}{2}}}simeq 2.938926261,R^{2}}$

An alternative formula is where d is the distance between parallel sides, or the height when the decagon stands on one side as base, or the diameter of the decagon’s inscribed circle.
By simple trigonometry,

${displaystyle d=2aleft(cos {tfrac {3pi }{10}}+cos {tfrac {pi }{10}}right),}$

and it can be written algebraically as

{displaystyle d=a{sqrt {5+2{sqrt {5}}}}.}

Sides[edit]

A regular decagon has 10 sides and is equilateral. It has 35 diagonals

Construction[edit]

As 10 = 2 × 5, a power of two times a Fermat prime, it follows that a regular decagon is constructible using compass and straightedge, or by an edge-bisection of a regular pentagon.^[4]

Construction of decagon

Construction of pentagon

An alternative (but similar) method is as follows:

Construct a pentagon in a circle by one of the methods shown in constructing a pentagon.
Extend a line from each vertex of the pentagon through the center of the circle to the opposite side of that same circle. Where each line cuts the circle is a vertex of the decagon. In other words, the image of a regular pentagon under a point reflection with respect of its center is a concentric congruent pentagon, and the two pentagons have in total the vertices of a concentric regular decagon.
The five corners of the pentagon constitute alternate corners of the decagon. Join these points to the adjacent new points to form the decagon.

Nonconvex regular decagon[edit]

The length ratio of two inequal edges of a golden triangle is the golden ratio, denoted by Phi , or its multiplicative inverse:

${displaystyle Phi -1={frac {1}{Phi }}=2,cos 72,^{circ }={frac {1}{,2,cos 36,^{circ }}}={frac {,{sqrt {5}}-1,}{2}}{text{.}}}$

So we can get the properties of a regular decagonal star, through a tiling by golden triangles that fills this star polygon.

The golden ratio in decagon[edit]

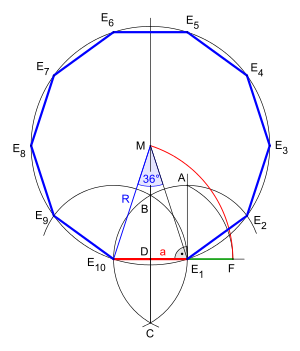
Both in the construction with given circumcircle^[5] as well as with given side length is the golden ratio dividing a line segment by exterior division the
determining construction element.

In the construction with given circumcircle the circular arc around G with radius GE₃ produces the segment AH, whose division corresponds to the golden ratio.

${displaystyle {frac {overline {AM}}{overline {MH}}}={frac {overline {AH}}{overline {AM}}}={frac {1+{sqrt {5}}}{2}}=Phi approx 1.618{text{.}}}$

In the construction with given side length^[6] the circular arc around D with radius DA produces the segment E₁₀F, whose division corresponds to the golden ratio.

${displaystyle {frac {overline {E_{1}E_{10}}}{overline {E_{1}F}}}={frac {overline {E_{10}F}}{overline {E_{1}E_{10}}}}={frac {R}{a}}={frac {1+{sqrt {5}}}{2}}=Phi approx 1.618{text{.}}}$

Decagon with given circumcircle,^[5] animation

Decagon with a given side length,^[6] animation

Symmetry[edit]

Symmetries of a regular decagon. Vertices are colored by their symmetry positions. Blue mirrors are drawn through vertices, and purple mirrors are drawn through edges. Gyration orders are given in the center.

The regular decagon has Dih₁₀ symmetry, order 20. There are 3 subgroup dihedral symmetries: Dih₅, Dih₂, and Dih₁, and 4 cyclic group symmetries: Z₁₀, Z₅, Z₂, and Z₁.

These 8 symmetries can be seen in 10 distinct symmetries on the decagon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway labels these by a letter and group order.^[7] Full symmetry of the regular form is r20 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.

Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g10 subgroup has no degrees of freedom but can seen as directed edges.

The highest symmetry irregular decagons are d10, an isogonal decagon constructed by five mirrors which can alternate long and short edges, and p10, an isotoxal decagon, constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular decagon.

Dissection[edit]

10-cube projection	40 rhomb dissection

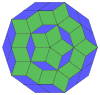
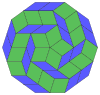
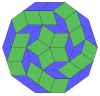
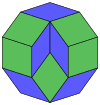
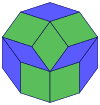
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms.^[8]
In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular decagon, m=5, and it can be divided into 10 rhombs, with examples shown below. This decomposition can be seen as 10 of 80 faces in a Petrie polygon projection plane of the 5-cube. A dissection is based on 10 of 30 faces of the rhombic triacontahedron. The list OEIS: A006245 defines the number of solutions as 62, with 2 orientations for the first symmetric form, and 10 orientations for the other 6.

Regular decagon dissected into 10 rhombi

5-cube

Skew decagon[edit]

3 regular skew zig-zag decagons

{5}#{ }	{5/2}#{ }	{5/3}#{ }

A regular skew decagon is seen as zig-zagging edges of a pentagonal antiprism, a pentagrammic antiprism, and a pentagrammic crossed-antiprism.

A skew decagon is a skew polygon with 10 vertices and edges but not existing on the same plane. The interior of such an decagon is not generally defined. A skew zig-zag decagon has vertices alternating between two parallel planes.

A regular skew decagon is vertex-transitive with equal edge lengths. In 3-dimensions it will be a zig-zag skew decagon and can be seen in the vertices and side edges of a pentagonal antiprism, pentagrammic antiprism, and pentagrammic crossed-antiprism with the same D_5d, [2⁺,10] symmetry, order 20.

These can also be seen in these 4 convex polyhedra with icosahedral symmetry. The polygons on the perimeter of these projections are regular skew decagons.

Orthogonal projections of polyhedra on 5-fold axes

Dodecahedron

Icosahedron

Icosidodecahedron

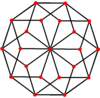Rhombic triacontahedron

Petrie polygons[edit]

The regular skew decagon is the Petrie polygon for many higher-dimensional polytopes, shown in these orthogonal projections in various Coxeter planes:^[9] The number of sides in the Petrie polygon is equal to the Coxeter number, h, for each symmetry family.

A₉	D₆	B₅
9-simplex	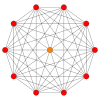4₁₁	1₃₁	5-orthoplex	5-cube

References[edit]

^ ^a ^b Sidebotham, Thomas H. (2003), The A to Z of Mathematics: A Basic Guide, John Wiley & Sons, p. 146, ISBN 9780471461630.
^ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 9, ISBN 9780521098595.
^ The elements of plane and spherical trigonometry, Society for Promoting Christian Knowledge, 1850, p. 59. Note that this source uses a as the edge length and gives the argument of the cotangent as an angle in degrees rather than in radians.
^ Ludlow, Henry H. (1904), Geometric Construction of the Regular Decagon and Pentagon Inscribed in a Circle, The Open Court Publishing Co..
^ ^a ^b Green, Henry (1861), Euclid’s Plane Geometry, Books III–VI, Practically Applied, or Gradations in Euclid, Part II, London: Simpkin, Marshall,& CO., p. 116. Retrieved 10 February 2016.
^ ^a ^b Köller, Jürgen (2005), Regelmäßiges Zehneck, → 3. Section «Formeln, Ist die Seite a gegeben …» (in German). Retrieved 10 February 2016.
^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
^ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
^ Coxeter, Regular polytopes, 12.4 Petrie polygon, pp. 223-226.

External links[edit]

Weisstein, Eric W. «Decagon». MathWorld.
Definition and properties of a decagon With interactive animation

Источник

Десятиугольник, виды, свойства и формулы.

Десятиугольник – это многоугольник, общее количество углов (вершин) которого равно десяти.

Десятиугольник, выпуклый и невыпуклый десятиугольник

Правильный десятиугольник (понятие и определение)

Построение правильного десятиугольника

Свойства правильного десятиугольника

Формулы правильного десятиугольника

Десятиугольник, выпуклый и невыпуклый десятиугольник:

Десятиугольник – это многоугольник с десятью углами.

Десятиугольник – это многоугольник, общее количество углов (вершин) которого равно десяти.

Десятиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый десятиугольник – это десятиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Звёздчатый десятиугольник – десятиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного десятиугольника многоугольника. Стороны звёздчатого десятиугольника могут пересекаться между собой.

Рис. 1. Выпуклый десятиугольник

Рис. 2. Невыпуклый десятиугольник

Сумма внутренних углов любого выпуклого десятиугольника равна 1440°.

Правильный десятиугольник (понятие и определение):

Правильный десятиугольник (декагон) – это правильный многоугольник с десятью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный десятиугольник – это десятиугольник, у которого все стороны равны, а все внутренние углы равны 144°.

Рис. 3. Правильный десятиугольник

Правильный десятиугольник имеет 10 сторон, 10 углов и 10 вершин.

Углы правильного десятиугольника образуют десять равнобедренных треугольников.

Правильный десятиугольник можно построить с помощью циркуля и линейки.

Построение правильного десятиугольника:

Постройте сначала правильный пятиугольник.
Соедините все его (правильного пятиугольника) вершины с центром описанной окружности прямыми до пересечения с этой же окружностью на противоположной стороне. В этих точках пересечения и находятся остальные пять вершин десятиугольника.
Соедините по порядку вершины правильного пятиугольника и пять точек, найденные шагом ранее. Искомый десятиугольник построен.

Свойства правильного десятиугольника:

Все стороны правильного десятиугольника равны между собой.

a₁ = a₂ = a₃ = a₄= a₅ = a₆ = a₇= a₈ = a₉ = a₁₀

Все углы равны между собой и составляют 144°.

α₁ = α₂ = α₃ = α₄ = α₅ = α₆ = α₇ = α₈ = α₉ = α₁₀ = 144°

Рис. 4. Правильный десятиугольник

Сумма внутренних углов любого правильного десятиугольника равна 1440°.
Все биссектрисы углов между сторонами равны и проходят через центр правильного десятиугольника O.

Рис. 5. Правильный десятиугольник

Количество диагоналей правильного десятиугольника равно 35.

Рис. 6. Правильный десятиугольник

(из каждой вершины правильного десятиугольника выходит 7 диагоналей)

Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр многоугольника O.

Рис. 7. Правильный десятиугольник

Формулы правильного десятиугольника:

Пусть a – сторона десятиугольника, r – радиус окружности, вписанной в десятиугольник, R – радиус описанной окружности десятиугольника, P – периметр десятиугольника, S – площадь десятиугольника.

Формулы стороны правильного десятиугольника:

Формулы периметра правильного десятиугольника:

Формулы площади правильного десятиугольника:

Формулы радиуса окружности, вписанной в правильный десятиугольник:

Формулы радиуса окружности, описанной вокруг правильного десятиугольника:

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности
104

Источник

Площадь правильного десятиугольника — это число, характеризующее правильный десятиугольник в единицах измерения площади.

Правильный десятиугольник (декагон) — это десятиугольник, у которого все стороны и углы равны.

Обозначения[править]

Введём обозначения:

a — длина стороны;

n — число сторон, n=10;

r — радиус вписанной окружности;

R — радиус описанной окружности;

α — половинный центральный угол, α=π/10;

P₁₀ — периметр правильного десятиугольника;

S_Δ — площадь равнобедренного треугольника с основанием, равным стороне, и боковыми сторонами, равными радиусу описанной окружности;

S₁₀ — площадь правильного десятиугольника.

Формулы[править]

Применима формула для площади правильного n-угольника при n=10:

${displaystyle S_{10}=5a^{2}ctg{frac {pi }{10}}Leftrightarrow }$

${displaystyle Leftrightarrow S_{10}=10S_{triangle }, S_{triangle }={frac {a^{2}}{4}}ctg{frac {pi }{10}}Leftrightarrow }$

${displaystyle Leftrightarrow S_{10}={frac {1}{2}}P_{10}r, P_{10}=10a, r={frac {a}{2}}ctg{frac {pi }{10}}Leftrightarrow }$

${displaystyle Leftrightarrow S_{10}=10R^{2}sin {frac {pi }{10}}cos {frac {pi }{10}}, R={frac {a}{2sin {frac {pi }{10}}}}Leftrightarrow }$

${displaystyle Leftrightarrow S_{10}=10r^{2}tg{frac {pi }{10}}, r=Rcos {frac {pi }{10}}}$

Используя значения тригонометрических функций углов для угла α=π/10:

${displaystyle S_{10}={frac {5{sqrt {5+2{sqrt {5}}}}}{2}}a^{2}Leftrightarrow }$

${displaystyle Leftrightarrow S_{10}=10S_{triangle }, S_{triangle }={frac {sqrt {5+2{sqrt {5}}}}{4}}a^{2}Leftrightarrow }$

${displaystyle Leftrightarrow S_{10}={frac {1}{2}}P_{10}r, P_{10}=10a, r={frac {sqrt {5+2{sqrt {5}}}}{2}}aLeftrightarrow }$

${displaystyle Leftrightarrow S_{10}={frac {5{sqrt {10-2{sqrt {5}}}}}{4}}R^{2}, R={frac {sqrt {{sqrt {5}}+1}}{2}}aLeftrightarrow }$

${displaystyle Leftrightarrow S_{10}=2{sqrt {25-10{sqrt {5}}}}r^{2}, r={frac {sqrt {10+2{sqrt {5}}}}{4}}R}$

где ${displaystyle sin {frac {pi }{10}}={frac {{sqrt {5}}-1}{4}}}$ , ${displaystyle cos {frac {pi }{10}}={frac {sqrt {10+2{sqrt {5}}}}{4}}}$ , ${displaystyle tg{frac {pi }{10}}={frac {sqrt {25-10{sqrt {5}}}}{5}}}$ , ${displaystyle ctg{frac {pi }{10}}={sqrt {5+2{sqrt {5}}}}}$

Другие многоугольники[править]

Площадь равностороннего треугольника;
Площадь квадрата;
Площадь правильного пятиугольника;
Площадь правильного шестиугольника;
Площадь правильного восьмиугольника;
Площадь правильного десятиугольника;
Площадь правильного двенадцатиугольника;
Площадь правильного шестнадцатиугольника;
Площадь правильного двадцатиугольника;
Площадь правильного n-угольника.

Источник

Видео: Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnline

Содержание

Обычный десятиугольник
Внутренние углы правильного десятиугольника
Сумма внутренних углов
Внешние углы
Количество диагоналей
Центр
Периметр
Площадь
Неправильный десятиугольник
Площадь неправильного десятиугольника по гауссовским определителям
Упражнение решено
Решение
Свойства Десятиугольника
Ссылки

В десятиугольник представляет собой плоскую фигуру в форме многоугольника с 10 сторонами и 10 вершинами или точками. Декагоны могут быть правильными или неправильными, в первом случае все стороны и внутренние углы имеют одинаковую величину, а во втором стороны и / или углы отличаются друг от друга.

На рисунке 1 показаны примеры десятиугольника каждого типа, и, как мы видим, правильный десятиугольник очень симметричен.

Основными элементами каждого десятиугольника являются:

-Стороны, отрезки линии, которые при соединении образуют десятиугольник.

-Vertices или точки между каждой последовательной стороной.

-Внутренние и внешние углы между соседними сторонами.

-Диагональные, сегменты, соединяющие две непоследовательные вершины.

Вершины названы заглавными буквами, как показано на рисунке 1, где использовались первые буквы алфавита, но можно использовать любую букву.

Стороны обозначены двумя буквами вершин, между которыми они находятся, например, сторона AB — это сторона между вершинами A и B. То же самое сделано с диагоналями, поэтому у нас есть диагональ AF, которая соединяет точки A и F.

Для углов мы используем этот символ: ∠, похожий на наклонную L. Например, угол ∠ ABC — это угол, вершиной которого является B, а сторонами являются отрезки AB и BC.

Обычный десятиугольник

В правильном десятиугольнике все стороны имеют одинаковую меру, как и внутренние углы. Поэтому говорят, что это равносторонний (равные стороны) и равносторонний (равные углы). Это очень симметричная фигура

Внутренние углы правильного десятиугольника

Чтобы найти меру внутренних углов правильного многоугольника, включая правильный десятиугольник, используется следующая формула:

Куда:

-I — мера угла в градусах.

-n — количество сторон многоугольника. В случае десятиугольника n = 10.

Подставляя n = 10 в предыдущую формулу, получаем следующее:

Говорят, что многоугольник выпуклый если его угловые размеры меньше 180 °, иначе многоугольник вогнутый. Поскольку любой внутренний угол правильного десятиугольника составляет 144º и меньше 180º, то это выпуклый многоугольник.

Сумма внутренних углов

Сумма внутренних углов любого многоугольника в градусах:

S = (n-2) x 180 °; n всегда больше 2

В этой формуле мы имеем:

-S — это сумма размеров внутренних углов.

-n — количество сторон. Для десятиугольника n = 10

Применяя формулу для n = 10, получаем:

S = (10 — 2) x 180º = 1440º

Внешние углы

Между одной стороной и продолжением соседней стороны образуется внешний угол, посмотрим:

Сумма угла ∠ ABC плюс внешний угол составляет 180 °, то есть они равны дополнительный. Следовательно, внешний угол равен 180º-144º = 36º, как мы видим на рисунке.

Количество диагоналей

Как было сказано ранее, диагонали — это отрезки, соединяющие непоследовательные вершины. Сколько диагоналей мы можем нарисовать в десятиугольнике? Когда количество вершин невелико, их легко сосчитать, но когда это число увеличивается, вы можете потерять счет.

К счастью, есть формула, по которой можно узнать, сколько диагоналей многоугольника. п стороны:

Подставляем десятиугольник n = 10 и получаем:

D = 10 х (10 — 3) / 2 = 35

В правильном десятиугольнике все диагонали пересекаются в одной точке, которая является центром фигуры:

Центр

Центр многоугольника определяется как точка, равноудаленная от любой вершины. На рисунке выше центр совпадает с точкой пересечения всех диагоналей.

Периметр

Если у правильного десятиугольника есть сторона a, его периметр P равен сумме всех сторон:

P = 10.a

Площадь

Зная длину к сбоку площадь правильного десятиугольника рассчитывается по формуле:

Приблизительная формула для площади:

И третий способ найти площадь — по длине апофемы L_К. Это сегмент, который соединяет середину одной стороны с центром многоугольника.

В этом случае площадь можно рассчитать по формуле:

Неправильный десятиугольник

Неправильный десятиугольник не является равносторонним или равноугольным, и обычно ему не хватает симметрии правильной фигуры, хотя некоторые десятиугольники могут иметь ось симметрии.

Они также могут быть выпуклыми или вогнутыми, если внутренние углы превышают 180º.

Неправильный десятиугольник на фиг. 1 вогнут, поскольку некоторые из его внутренних углов больше 180 °. Ясно, что существует множество комбинаций углов и сторон, которые приводят к неправильному десятиугольнику.

В любом случае верно, что:

-Внутренние углы неправильного десятиугольника также составляют в сумме 1440º.

-Также имеет 35 диагоналей.

Площадь неправильного десятиугольника по гауссовским определителям

В общем, не существует единой формулы для определения площади неправильного многоугольника, поскольку стороны и углы разные. Однако его можно найти, зная координаты вершин и вычисливГауссовские детерминанты:

-Позвоним (х_п , Y_п) к координатам вершин, причем п варьируется от 1 до 10.

-Вы можете начать с любой вершины, до которой координаты (x₁, Y₁). Теперь нам нужно подставить значения каждой координаты в эту формулу:

Где детерминанты — это именно операции в скобках.

-Важно отметить, что последний определитель снова включает первую вершину вместе с последней. Для десятиугольника это будет выглядеть так:

(Икс₁₀Y₁ — Икс₁Y₁₀)

Важный: Полоски имеют абсолютное значение и означают, что окончательный результат дается с положительным знаком. всегда.

Процедура может быть трудоемкой, если у фигуры много вершин, в случае с десятиугольником — 10 операций, поэтому желательно составить таблицу или список.

Упражнение решено

Вычислите площадь неправильного десятиугольника, показанного на рисунке. Координаты вершин — A, B, C… J, значения которых показаны слева.

Решение

-Делаем каждую из 10 операций:

2×6 – 4×0 = 12 – 0 =12
0×4 – 6×(-2) = 0 + 12 =12
(-2)×7- 4×(-5) = -14 + 20 = 6
(-5)×2 – 7×(-6) = -10 + 42 = 32
(-6)×(-4) – 2×(-4) = 24 + 8 =32
(-4)×(-2) – (-4)×(-2) = 8 – 8 =0
(-2)×0 – (-2)×(-1) =0 -2
(-1)×0 – 0×(2) = 0 – 0 = 0
2×2 – 0×8 = 4 – 0 = 4
8×4 -2×2 = 32 – 4 = 28

-Давайте добавим результаты:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Положительный результат получается даже без столбцов абсолютного значения, но если он отрицательный, знак меняется.

-Предыдущий результат делится на 2, и это площадь многоугольника:

А = 124/2 = 62

Свойства Десятиугольника

Вот краткое изложение общих свойств десятиугольника, правильного или неправильного:

-У него 10 сторон и 10 вершин.

-Сумма внутренних углов 1440º.

-Есть 35 диагоналей.

-Периметр — это сумма всех сторон.

-Вы можете создавать треугольники внутри многоугольника, рисуя сегменты от одной вершины ко всем остальным. В десятиугольнике можно нарисовать 8 треугольников таким образом, как показано ниже:

Ссылки

Александр, Д. 2013. Геометрия. 5-е. Издание. Cengage Learning.
Decagon.com. Декагон. Получено с: decagono.com
Открытый справочник по математике. Декагон. Получено с: mathopenref.com.
Sangaku Maths. Элементы многоугольника и их классификация. Получено с: sangakoo.com.
Википедия. Декагон. Получено с: es.wikipedia.com.

Источник

Содержание

Обозначения

Формулы:

n=10:

α=π/10:

Другие многоугольники:

Ссылки

Regular decagon[edit]

Side length[edit]

Area[edit]

Sides[edit]

Construction[edit]

Nonconvex regular decagon[edit]

The golden ratio in decagon[edit]

Symmetry[edit]

Dissection[edit]

Skew decagon[edit]

Petrie polygons[edit]

See also[edit]

References[edit]

External links[edit]

Десятиугольник, виды, свойства и формулы.

Десятиугольник, выпуклый и невыпуклый десятиугольник:

Правильный десятиугольник (понятие и определение):

Построение правильного десятиугольника:

Свойства правильного десятиугольника:

Формулы правильного десятиугольника:

Обозначения[править]

Формулы[править]

Другие многоугольники[править]

Содержание

Обычный десятиугольник

Внутренние углы правильного десятиугольника

Сумма внутренних углов

Внешние углы

Количество диагоналей

Центр

Периметр

Площадь

Неправильный десятиугольник

Площадь неправильного десятиугольника по гауссовским определителям

Упражнение решено

Решение

Свойства Десятиугольника

Ссылки