Как найти площадь правильного девятиугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Вычисление девятиугольника (фигура с девятью вершинами). Введите одно известное значение, затем нажмите кнопку вычислить.

Поделиться расчетом:

Калькулятор девятиугольника, введите одно известное значение

Длина стороны(a)

Меньшая диагональ(d1)

Средняя диагональ(e)

Большая диагональ(d3)

Высота(h)

Периметр(p)

Площадь(S)

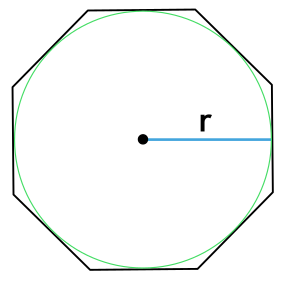
Радиус описанной окружности(R)

Радиус вписанной окружности(r)

Вычислить

Очистить

Формулы:

a = 2 * R * sin( π / 9 )
d = 2 * R * sin( 2 * π / 9 )
e = 2 * R * sin( 3 * π / 9 )
f = 2 * R * sin( 4 * π / 9 )
h = R + r
p = 9 * a
S = 9/2 * R * sin( 2 * π / 9 )
r = a / 2 * tan( π / 9 )
Угол: 140°, 27 диагоналей.

Источник

Каким способом считать:

Через тангенс

Через радиус вписанной окружности

Укажите размеры:

Количество сторон

Длина одной стороны

Площадь:

Решение:

Ссылка на страницу с результатом:

# Теория

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Правильный многоугольник так же называют правильным n-угольником, где n — это количество сторон в многоугольнике (пятиугольник, шестиугольник и т.д.).

В любой правильный многоугольник можно вписать окружность. Такая окружность называется вписанной окружностью.

Около любого правильного многоугольника можно описать окружность.

Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.

Формулы площади правильного многоугольника

S = dfrac {n cdot a^2}{4 cdot tg lparen dfrac{360degree}{2n} rparen}

S = dfrac {n cdot a^2}{4 cdot tg lparen dfrac{180degree}{n} rparen}

S — площадь правильного многоугольника
n — количество сторон
a — длина стороны
tg — тангенс

Площадь правильного многоугольника через радиус вписанной окружности

S = p cdot r

S = dfrac{1}{2} cdot n cdot a cdot r

S — площадь правильного многоугольника
p — полупериметр правильного многоугольника
r — радиус вписанной окружности правильного многоугольника
n — количество сторон
a — сторона правильного многоугольника

p = dfrac{n cdot a}{2}

Войдите чтобы писать комментарии

Источник

На странице собраны калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного многоугольника по стороне и количеству сторон, а также зная радиус вписанной и описанной окружностей.

Содержание:

калькулятор площади правильного многоугольника
формула площади правильного многоугольника через длину стороны
формула площади правильного многоугольника радиус вписанной окружности
формула площади правильного многоугольника радиус описанной окружности
пример задачи

Формула площади правильного многоугольника через длину стороны и число сторон

S = dfrac{na^2}{4} cdot ctg dfrac{180°}{n}

a — длина стороны многоугольника

n — число сторон многоугольника

Формула площади правильного многоугольника через радиус вписанной окружности

S = nr^2 tg dfrac{180°}{n}

r — радиус вписанной в многоугольник окружности

n — число сторон многоугольника

Формула площади правильного многоугольника через радиус описанной окружности

S = dfrac{nR^2}{2} cdot sin dfrac{360°}{n}

R — радиус описанной в многоугольник окружности

n — число сторон многоугольника

Пример задачи на нахождение площади правильного многоугольника

Задача 1

Найдите площадь правильного n-угольника, если n = 6, r = 9 см, где r — радиус вписанной окружности.

Решение

Чтобы решить эту задачу мы используем вторую формулу.

S = nr^2 tg dfrac{180°}{n} = 6 cdot 9^2 cdot tg dfrac{180°}{6} = 6 cdot 81 cdot tg 30° = 486 cdot tg 30° = 486 cdot 0.57735027 approx 280.59223 : см^2

Ответ: 486 cdot tg 30° approx 280.59223 : см^2

Чтобы проверить ответ воспользуемся калькулятором .

Источник

Правильный девятиугольник

Площадь правильного девятиугольника — это число, характеризующее девятиугольник в единицах измерения площади.

Правильный девятиугольник — это девятиугольник у которого все стороны и углы равны.

Содержание

1 Обозначения
2 Формулы:
- 2.1 n=9:
3 Другие многоугольники:
4 Ссылки

Обозначения

Введём обозначения:

a — длина стороны;

n — число сторон, n=9;

r — радиус вписанной окружности;

R — радиус описанной окружности;

α — половинный центральный угол, α=π/9;

P₉ — периметр правильного девятиугольника;

S_Δ — площадь равнобедренного треугольника с основанием равным стороне и боковыми сторонами равными радиусу описанной окружности;

S₉ — площадь правильного семиугольника.

Формулы:

n=9:

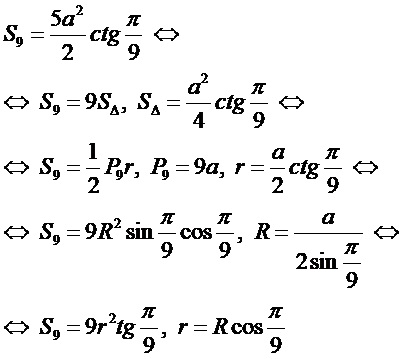
Другие многоугольники:

Ссылки

Участник:Logic-samara

Источник

Загрузить PDF

Правильный многоугольник представляет собой двумерную выпуклую фигуру, у которой все стороны и углы равны. Площадь некоторых многоугольников, таких как треугольников или четырехугольников, можно найти по простым формулам, но если у многоугольника больше четырех сторон, воспользуйтесь формулой, в которую входит апофема и периметр фигуры.

1

Вычислите периметр. Периметр равен сумме всех сторон многоугольника. Если многоугольник правильный, периметр равен произведению одной стороны на число сторон «n».^[1]
2
Найдите апофему. Апофема — это перпендикуляр, опущенный из центра многоугольника на любую из его сторон. Найти апофему немного сложнее, чем периметр.
- Формула для вычисления апофемы: а = s/(2tg(180/n)), где «s» — сторона, «n» — число сторон.
3

Запишите формулу для вычисления площади. Площадь любого правильного многоугольника вычисляется по формуле: S = (a * p)/2, где «a» — апофема, «p» — периметр.
4
Подставьте значения «а» и «р» в формулу, чтобы вычислить площадь. Для примера рассмотрим шестиугольник (n = 6), сторона которого равна 10 см (s = 10).
- Периметр: р = n * s = 6 * 10 = 60.
- Вычислите апофему. а = s/(2tg(180/n)) = 10/(2tg(180/6)) = 10/1,1547 = 8,66.
- Площадь многоугольника: S = (a * p)/2 = (8,66 * 60)/2 = 259,8 см².
- Обратите внимание, что (8,66 * 60)/2 = (8,66/2) * 60 = 8,66 * (60/2), то есть на 2 можно сначала разделить апофему или периметр, а не произведение апофемы и периметра. При этом вы получите один и тот же результат.
Реклама

1

Представьте правильный многоугольник как совокупность нескольких треугольников. Каждая сторона многоугольника представляет собой основание треугольника; таким образом, число треугольников равно числу сторон многоугольников. Все треугольники равны, то есть равны их стороны и высоты.^[2]
2

Вспомните формулу для вычисления площади треугольника. S = 1/2bh, где «b» — основание треугольника (которое совпадает со стороной многоугольника), «h» — высота треугольника (которая совпадает с апофемой правильного многоугольника).^[3]
3

Обратите внимание на сходство формул. Формула для вычисления площади правильного многоугольника S = 1/2аp, где «а» — сторона многоугольника, «р» — периметр многоугольника. Периметр равен стороне, умноженной на число сторон («n»); в правильном многоугольнике «n» равно числу треугольников, составляющих многоугольник. Таким образом, формула для вычисления площади многоугольника представляет собой формулу для вычисления площади треугольника, умноженную на количество треугольников в многоугольнике.^[4]

Реклама

Советы

Если правильный многоугольник разделен на треугольники, а площадь одного треугольника дана, вычислять апофему не нужно. Просто умножьте площадь одного треугольника на количество сторон многоугольника.

Об этой статье

Эту страницу просматривали 27 523 раза.

Была ли эта статья полезной?

Источник