Как найти площадь правильного многоугольника через радиус - Исправление недочетов и поиск решений вместе с Examum.ru

На странице собраны калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного многоугольника по стороне и количеству сторон, а также зная радиус вписанной и описанной окружностей.

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Содержание:

калькулятор площади правильного многоугольника
формула площади правильного многоугольника через длину стороны
формула площади правильного многоугольника радиус вписанной окружности
формула площади правильного многоугольника радиус описанной окружности
пример задачи

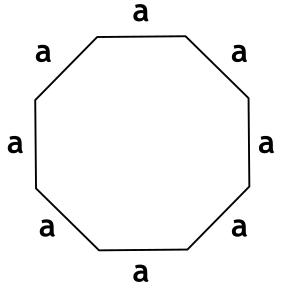
Формула площади правильного многоугольника через длину стороны и число сторон

S = dfrac{na^2}{4} cdot ctg dfrac{180°}{n}

a — длина стороны многоугольника

n — число сторон многоугольника

Формула площади правильного многоугольника через радиус вписанной окружности

S = nr^2 tg dfrac{180°}{n}

r — радиус вписанной в многоугольник окружности

n — число сторон многоугольника

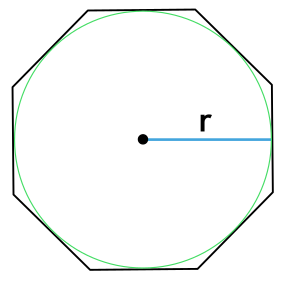
Формула площади правильного многоугольника через радиус описанной окружности

S = dfrac{nR^2}{2} cdot sin dfrac{360°}{n}

R — радиус описанной в многоугольник окружности

n — число сторон многоугольника

Пример задачи на нахождение площади правильного многоугольника

Задача 1

Найдите площадь правильного n-угольника, если n = 6, r = 9 см, где r — радиус вписанной окружности.

Решение

Чтобы решить эту задачу мы используем вторую формулу.

S = nr^2 tg dfrac{180°}{n} = 6 cdot 9^2 cdot tg dfrac{180°}{6} = 6 cdot 81 cdot tg 30° = 486 cdot tg 30° = 486 cdot 0.57735027 approx 280.59223 : см^2

Ответ: 486 cdot tg 30° approx 280.59223 : см^2

Чтобы проверить ответ воспользуемся калькулятором .

Источник

Площадь правильного многоугольника по радиусу описанной окружности и количеству сторон

Калькулятор рассчитывает площадь правильного многоугольника по радиусу описанной около многоугольника окружности и количеству сторон.

Введите радиус описанной окружности R

Введите количество сторон многоугольника n

Формула площади правильного многоугольника по радиусу описанной около многоугольника окружности и количеству сторон

Где R — радиус описанной около правильного многоугольника окружности,
n — количество сторон правильного многоугольника

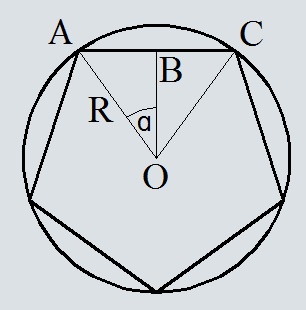
Вывод формулы площади правильного многоугольника по радиусу описанной около многоугольника окружности и количеству сторон

Треугольники AOB и COB равны и являются прямоугольными.

AO=OC=R.

Угол α будет равен 360 градусов/(количество сторон * 2)

Площадь треугольника ACO будет равно произведению половины основания AC=2×AB на высоту BO

Затем умножим площадь треугольника ACO на количество сторон правильного многоугольника и получим площадь правильного многоугольника

Заменим sin(2α)=2sin(α)cos(α) и подставим вместо α ранее выведенную формулу

Похожие калькуляторы

Источник

Найдём площадь правильного многоугольника через радиусы вписанной и описанной окружностей и через его сторону.

Любой правильный многоугольник вписан в окружность и описан около окружности. Центры вписанной и описанной окружностей совпадают и называются центром правильного многоугольника.

Соединив центр правильного n-угольника

$[{A_1}{A_2}{A_3}{A_4}...{A_{n - 1}}{A_n}]$

со всеми его вершинами, получим n равнобедренных треугольников.

Основание каждого такого треугольника равно стороне многоугольника, боковые стороны равны радиусу описанной около многоугольника окружности угол при вершине — центральному углу правильного многоугольника

$[{A_1}{A_2} = a,]$

$[O{A_1} = O{A_2} = R,]$

$[angle {A_1}O{A_2} = frac{{{{360}^o}}}{n}]$

Так как площадь треугольника равна половине произведения его сторон на синус угла между ними,

$[{S_{Delta {A_1}O{A_2}}} = frac{1}{2} cdot {A_1}O cdot {A_2}O cdot sin angle {A_1}O{A_2}.]$

Отсюда

$[{S_{Delta {A_1}O{A_2}}} = frac{1}{2} cdot {R^2} cdot sin frac{{{{360}^o}}}{n}.]$

Поскольку многоугольник состоит из n таких треугольников, формула площади правильного многоугольника через радиус описанной окружности:

$[S = frac{1}{2} cdot {R^2} cdot n cdot sin frac{{{{360}^o}}}{n}.]$

Проведём в треугольнике A1OA2 высоту OF. Её длина равна радиусу вписанной в правильный n-угольник окружности:

По свойству равнобедренного треугольника OF является также его биссектрисой и медианой:

$[angle {A_1}OF = frac{1}{2}angle {A_1}O{A_2} = frac{1}{2} cdot frac{{{{360}^o}}}{n} = frac{{{{180}^o}}}{n},]$

$[{A_1}F = frac{1}{2}{A_1}{A_2}.]$

Из прямоугольного треугольника A1OF по определению тангенса

$[tgangle {A_1}OF = frac{{{A_1}F}}{{OF}},]$

откуда

$[{A_1}F = OF cdot tgangle {A_1}OF = r cdot tgfrac{{{{180}^o}}}{n}.]$

Так как площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне,

$[{S_{Delta {A_1}O{A_2}}} = frac{1}{2} cdot {A_1}{A_2} cdot OF = {A_1}Fcdot OF,]$

$[{S_{Delta {A_1}O{A_2}}} = r cdot tgfrac{{{{180}^o}}}{n} cdot r = {r^2} cdot tgfrac{{{{180}^o}}}{n}.]$

Площадь

$[{A_1}{A_2}{A_3}{A_4}...{A_{n - 1}}{A_n}]$

равна сумме n таких площадей.

Таким образом, формула площади правильного многоугольника через радиус вписанной окружности:

$[S = {r^2} cdot n cdot tgfrac{{{{180}^o}}}{n}.]$

Из треугольника A1OF

$[OF = frac{{{A_1}F}}{{tgangle {A_1}OF}} = frac{{frac{1}{2}{A_1}{A_2}}}{{tgangle {A_1}OF}} = frac{a}{{2tgfrac{{{{180}^o}}}{n}}}.]$

Следовательно,

$[{S_{Delta {A_1}O{A_2}}} = {A_1}F cdot OF = frac{1}{2}a cdot frac{a}{{2tgfrac{{{{180}^o}}}{n}}} = frac{{{a^2}}}{{4tgfrac{{{{180}^o}}}{n}}}.]$

Поскольку многоугольник состоит из n равных треугольников, формула площади правильного многоугольника через его сторону:

$[S = frac{{{a^2} cdot n}}{{4tgfrac{{{{180}^o}}}{n}}}.]$

Источник

Формула для вычисления площади правильного многоугольника по сторонам и длине каждой стороны:

S = N ⋅ a² / (4 ⋅ tg(180 / π)),

где N — количество сторон, a — длина стороны, π = константа равная (3.14).

Формула для вычисления площади правильного многоугольника через радиус вписанной окружности:

S = N ⋅ r² ⋅ tg(180 / π),

где N — количество сторон, r — радиус вписанной окружности, π = константа равная (3.14).

Формула для вычисления площади правильного многоугольника через радиус описанной окружности:

S = N ⋅ R² ⋅ sin(360 / π) / 2,

где N — количество сторон, R — радиус описанной окружности, π = константа равная (3.14).

Источник

Площадь правильного многоугольника

Онлайн калькулятор — площадь правильного многоугольника

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Правильный многоугольник так же называют правильным n-угольником, где n — это количество сторон в многоугольнике (пятиугольник, шестиугольник и т.д.).

В любой правильный многоугольник можно вписать окружность. Такая окружность называется вписанной окружностью.

Около любого правильного многоугольника можно описать окружность.

Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.

Площадь правильного многоугольника

Соединив центр правильного n-угольника

со всеми его вершинами, получим n равнобедренных треугольников.

Так как площадь треугольника равна половине произведения его сторон на синус угла между ними,

Проведём в треугольнике A1OA2 высоту OF. Её длина равна радиусу вписанной в правильный n-угольник окружности:

По свойству равнобедренного треугольника OF является также его биссектрисой и медианой:

Из прямоугольного треугольника A1OF по определению тангенса

Так как площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне,

равна сумме n таких площадей.

Таким образом, формула площади правильного многоугольника через радиус вписанной окружности:

Из треугольника A1OF

Формула площади правильного многоугольника

Правильный многоугольник так же называют правильным n-угольником , где n — это количество сторон в многоугольнике (пятиугольник, шестиугольник и т.д.).

Около любого правильного многоугольника можно описать окружность.

источники:

Площадь правильного многоугольника

http://calcsbox.com/post/formula-plosadi-pravilnogo-mnogougolnika.html

Источник