Как найти площадь поверхности усеченной пирамиды
На данной странице калькулятор поможет рассчитать площадь поверхности пирамиды онлайн. Для расчета задайте периметры оснований и апофему.
Усеченная пирамида — многогранник, образованный пирамидой и её сечением, параллельным основанию.
Апофема – опущенный перпендикуляр из вершины на ребро основания.
Боковая поверхность через периметры и апофему
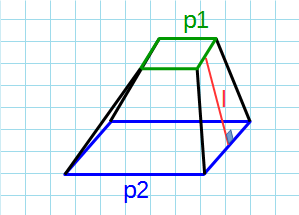
Формула площади боковой поверхности усеченной пирамиды через периметры и апофему:
p1 — периметр верхнего основания; p2 — периметр нижнего основания; l — апофема усеченной пирамиды.
Усечённой пирамидой называется часть пирамиды между её основанием и плоскостью, параллельной ему.
Усечённая пирамида, полученная из правильной пирамиды сечением, параллельным её основанию, называется правильной усечённой пирамидой.
|
|
 |
| Рис. (1). Правильная усечённая треугольная пирамида (ABCKNV)
(ABC) и (KNV) — основания пирамиды, OO1 — высота. |
Рис. (2). Правильная усечённая четырёхугольная пирамида (ABCDZVNK) (ABCD) и (ZVNK) — основания, OO1 — высота |
Объём усечённой пирамиды:
.
Площадь боковой поверхности правильной усечённой пирамиды:
;
(h) — апофема правильной усечённой пирамиды, на данных рисунках это отрезок (LF).
|
Рис. (3). Апофема правильной треугольной усечённой пирамиды |
Рис. (4). Апофема правильной четырёхугольной усечённой пирамиды |
Источники:
Рис .1. Правильная усечённая треугольная пирамида ABCKNV. © ЯКласс.
Рис.2. Правильная усечённая четырёхугольная пирамида ABCDZVNK. © ЯКласс.
Рис. 3. Апофема правильной треугольной усечённой пирамиды. © ЯКласс.
Рис. 4. Апофема правильной четырёхугольной усечённой пирамиды. © ЯКласс.
Онлайн калькулятор площади боковой поверхности усеченной пирамиды
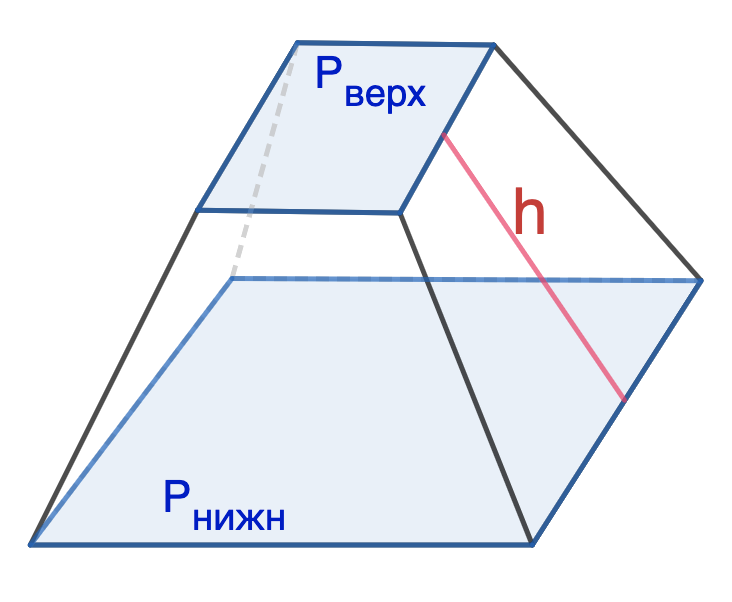
Периметр верхнего основания (P1)
Периметр нижнего основания (P2)
Апофема (h)
Формула
(S_{бок} = frac{1}{2}*(P_1+P_2)*h)
(P_1, P_2) — периметры оснований,
h — апофема.
Онлайн калькулятор рассчитает площадь боковой поверхности любой правильной усеченной пирамиды, то есть пирамиды с правильным многоугольником в основании.
Усеченная пирамида – это многогранник, который образуется основанием пирамиды и параллельным ему сечением. Можно сказать, что усеченная пирамида – это пирамиду со срезанной верхушкой. Эта фигура обладает множеством уникальных свойств:
- Боковые грани пирамиды являются трапециями;
- Боковые ребра правильной усеченной пирамиды одинаковой длины и наклонены к основанию под одинаковым углом;
- Основания являются подобными многоугольниками;
- В правильной усеченной пирамиде, грани представляют собой одинаковые равнобедренные трапеции, площадь которых равна. Также они наклонены к основанию под одним углом.
Формула площади боковой поверхности усеченной пирамиды представляет собой сумму площадей ее сторон:
Так как стороны усеченной пирамиды представляют собой трапеции, то для расчета параметров придется воспользоваться формулой площади трапеции. Для правильной усеченной пирамиды можно применить другую формулу расчета площади. Так как все ее стороны, грани, и углы при основании равны, то можно применить периметры основания и апофему, а также вывести площадь через угол при основании.
Если по условиям в правильной усеченной пирамиде даны апофема (высота боковой стороны) и длины сторон основания, то можно произвести расчет площади через полупроизведение суммы периметров оснований и апофемы:
Давайте рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная пятиугольная пирамида. Апофема l = 5 см, длина грани в большом основании равна a = 6 см, а грань в меньшем основании b = 4 см. Рассчитайте площадь усеченной пирамиды.
Для начала найдем периметры оснований. Так как нам дана пятиугольная пирамида, мы понимаем, что основания представляют собой пятиугольники. Значит, в основаниях лежит фигура с пятью одинаковыми сторонами. Найдем периметр большего основания:
Таким же образом находим периметр меньшего основания:
Теперь можем рассчитывать площадь правильной усеченной пирамиды. Подставляем данные в формулу:
Таким образом, мы рассчитали площадь правильной усеченной пирамиды через периметры и апофему.
Еще один способ расчета площади боковой поверхности правильной пирамиды, это формула через углы у основания и площадь этих самых оснований.
Давайте рассмотрим пример расчета. Помним, что данная формула применяется только для правильной усеченной пирамиды.
Пусть дана правильная четырехугольная пирамида. Грань нижнего основания a = 6 см, а грань верхнего b = 4 см. Двухгранный угол при основании β = 60°. Найдите площадь боковой поверхности правильной усеченной пирамиды.
Для начала рассчитаем площадь оснований. Так как пирамида правильная, все грани оснований равны между собой. Учитывая, что в основании лежит четырехугольник, понимаем, что нужно будет рассчитать площадь квадрата. Она представляет собой произведение ширины на длину, но в квадрате эти значения совпадают. Найдем площадь большего основания:
Теперь используем найденные значения для расчета площади боковой поверхности.

Зная несколько несложных формул, мы легко рассчитали площадь боковой трапеции усеченной пирамиды через различные значения.












