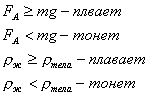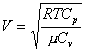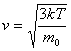формулы по физике
4
Площади
l
– длинна
b
— высота, ширина.
Площадь круга:
Кинематика.
Равномерное
движение:
a
= 0
V
= S/t
Ускоренное движение:
a
> 0
a
= (V
– V0
)/ t
S
= S0
+ V0t
(at2
)/2
a
= (V2
– V02
)/ 2S
Последовательный
ряд нечетных чисел:
— ую:
просто:
Движение под
углом к горизонту.
Скорость по оси
ОХ:
Скорость по оси
ОУ:
Максимальное время
подъема:
tполн
= 2t
Расстояние :
S
= Vxtполн.
Максимальная
высота:
Движение тела,
брошенного горизонтально:
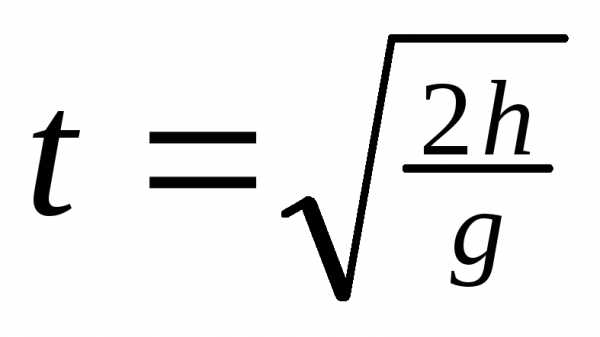

F
= ma
P
= mg
Fтр.
= -N
F
= -F
Момент сил.
M=Fl
M1+M2+…+Mn = 0
Пружина.
x
– удлинение.
k
– кооф. растяжения.
l
= l
– l0
l
– абсолют. удлинение пружины.
ε
-относит. удлинение.
l0
– начальная длинна
Работа и энергия.
;
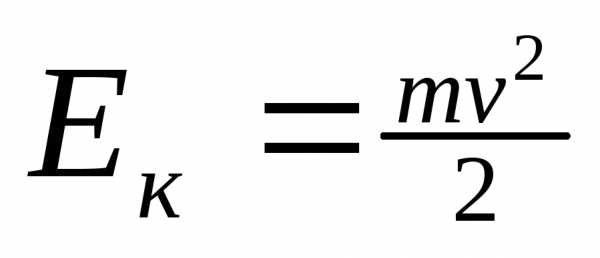
Движение по окр-ти.
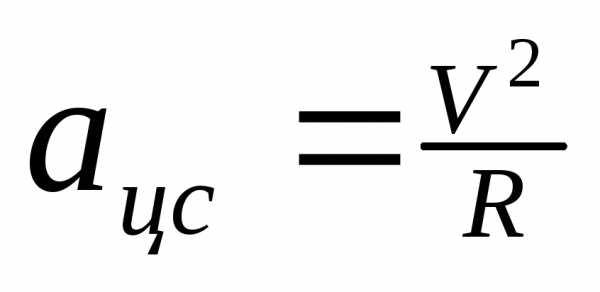
w
— угловая скорость.[рад/с]
v
-линейная скорость.
n
— частота обращения. [об./мин.]
T
– период обращения. [время]
Угловая скорость.
Период обращения.
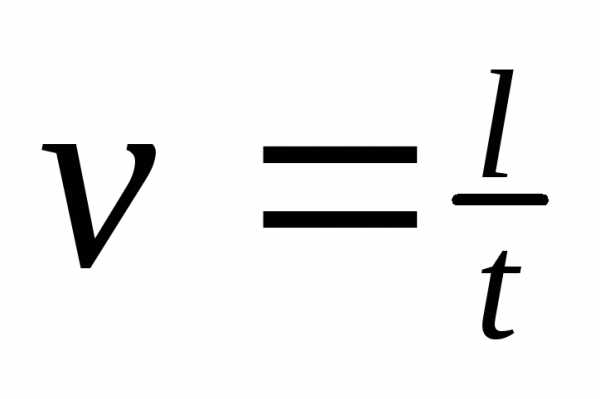
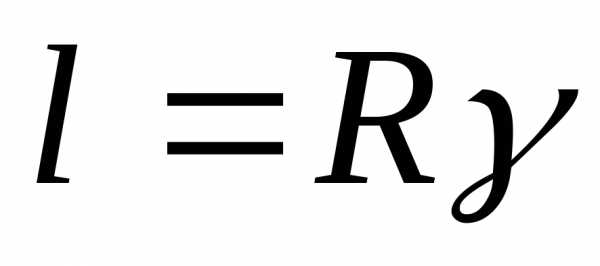
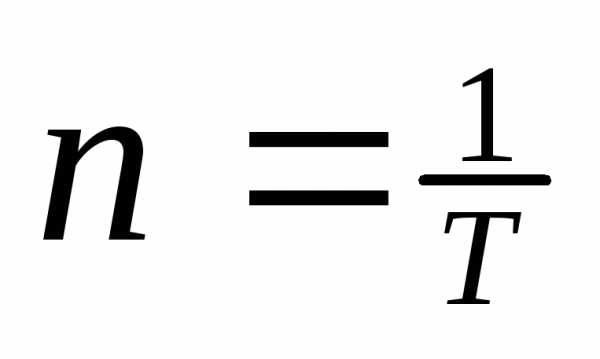
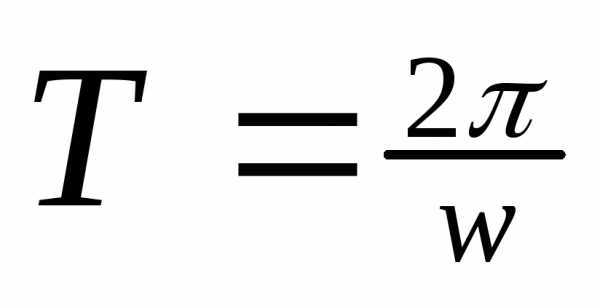
Для случаев, когда
n
= [обороты]
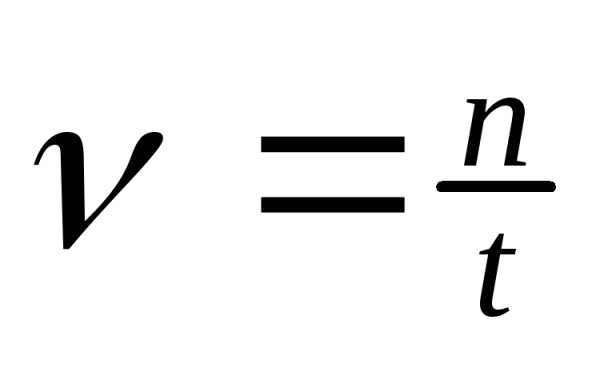
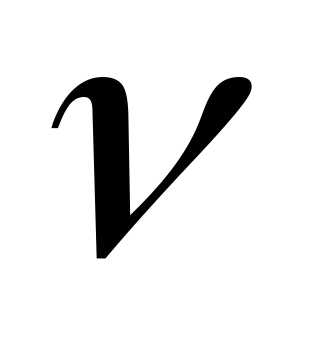
частота [1/с = 1 Гц]

угол.
l
– длинна дуги.
Импульс.
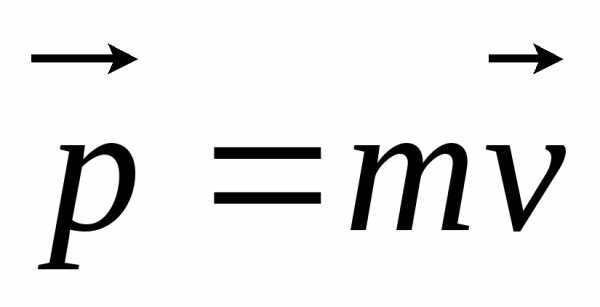
Не упругое вз-вие.
до: после:
в проекции на ось
х:
Упругое соударение.
до вз-я: после:
в проекции на ось
х:
Реактивное движение:
в проекции на ось
х: (вверх)
║
0 изначально.
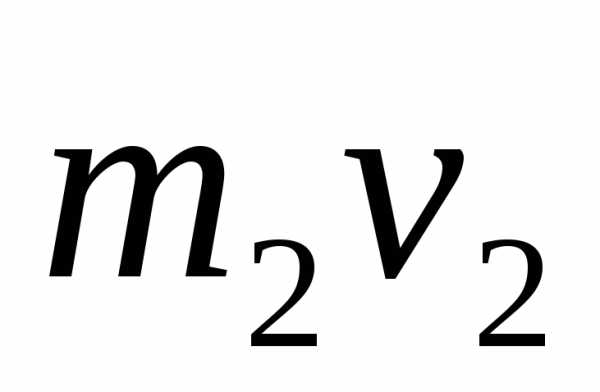
импульс газов
Импульс силы.
Механика жидкостей
и газов.
Давление. Закон
Паскаля.
-//- жидкости на дно
сосуда.
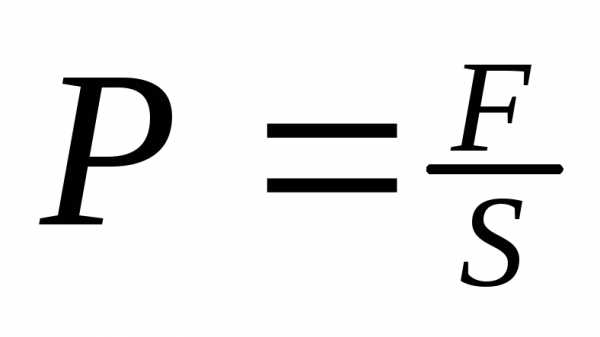
F
– сила давления
S
– поверхность[1Па = 1Н/1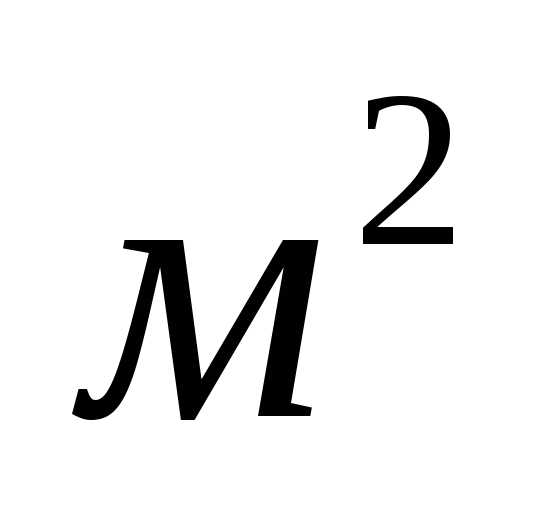
h
– высота уровня жидкости.
Сообщающиеся
сосуды.

Архимедова сила.
Атм. давление
;
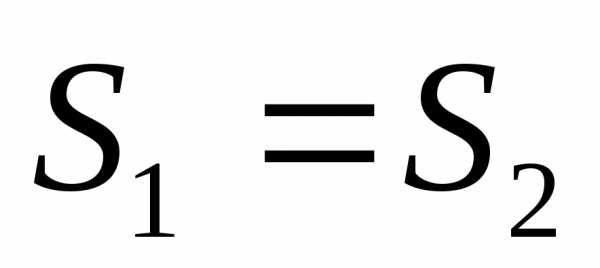
/
вытесненной жидкости
цилиндром.
Закон Гука. Растягив.
сила.
l
–первоначальная длинна стержня
Δl
–абсолютное удлинение
S
–площадь поперечного сеч.
E
–кооф. пропорцион., модуль Юнга, модуль
упругости.

-закон
Гука
КПД машин.
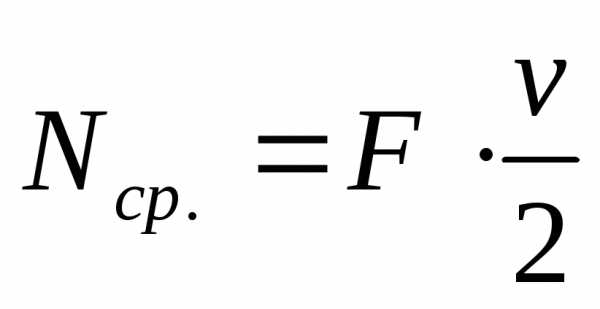
[1дж/1с = 1 Вт]
Колебания и волны.
Звук.
F
– возвращающая сила
k
– постоянная возвращающ.
x
– смещение
Маятник.

– длинна маятника
Математический
маятник – точка, подвешенная на невесомой
и нерастяжимой нити.
Пружинный маятник:
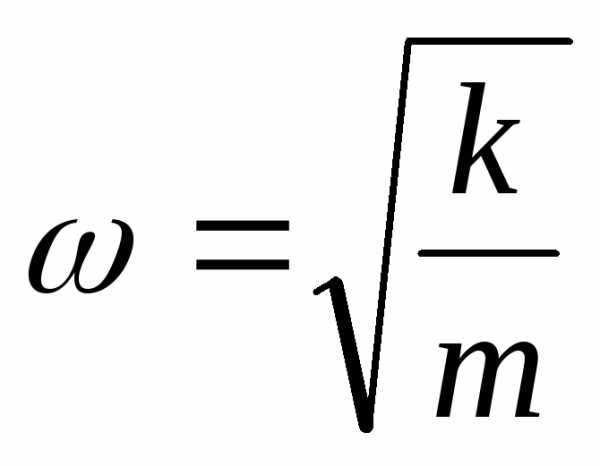
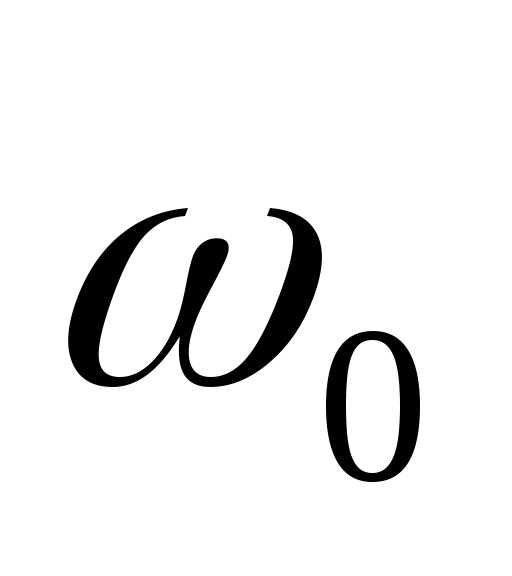
циклическая частота колебаний
Фаза колебаний.

угловая скорость

угол поворота
Скорость
распространения волн

Электромагнитные
колебания.
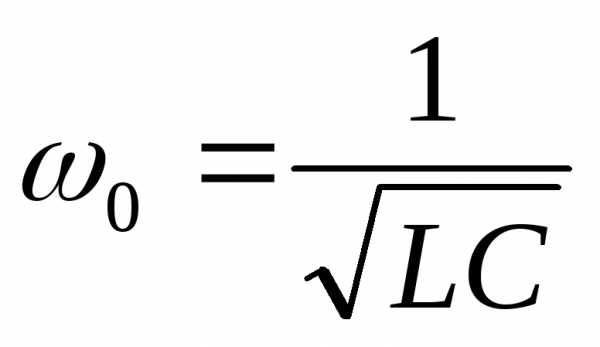
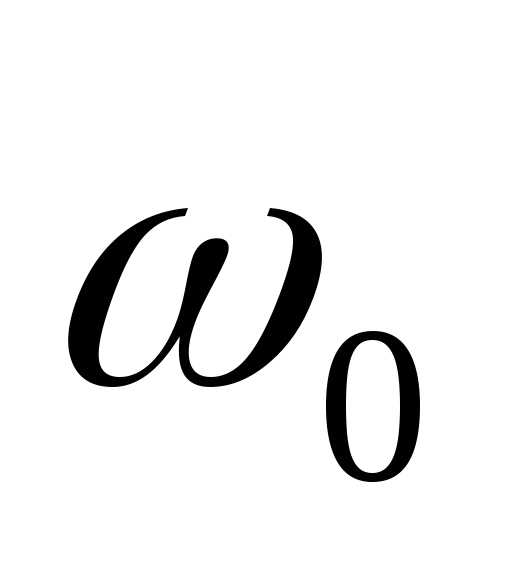
собственна частота колебаний в контуре
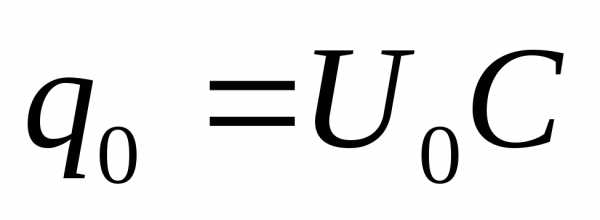
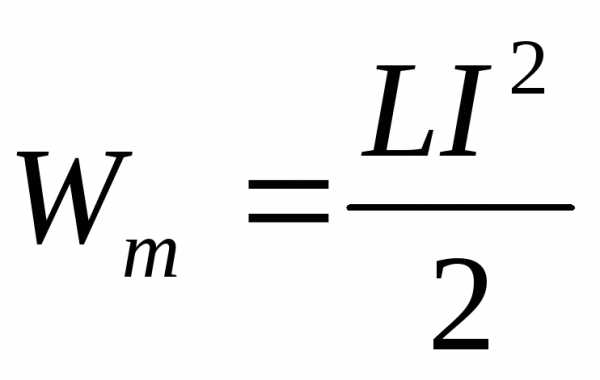
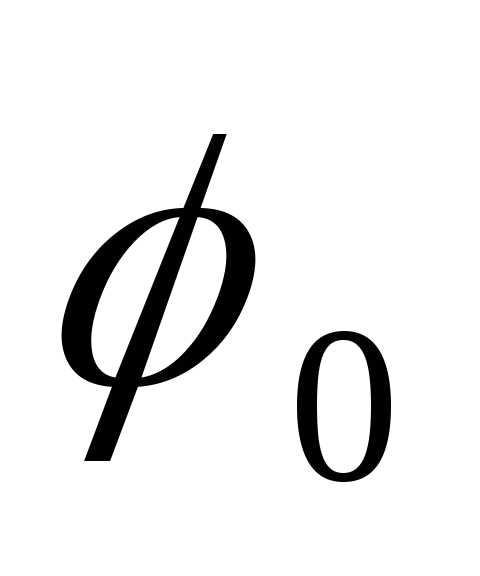
фаза
колебаний
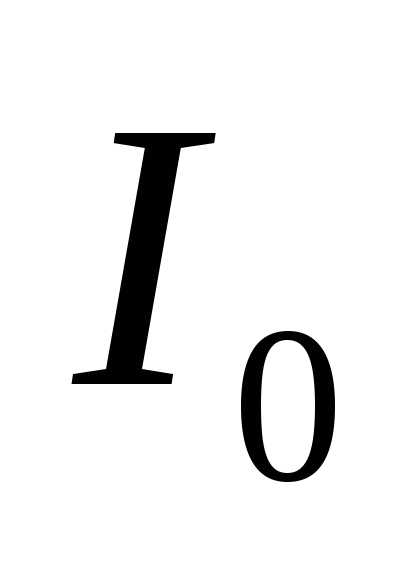
амплитуда тока
С – скорость в
ваакуме
n
– абс. показатель преломления среды
Молекулярно-кинетическая
теория

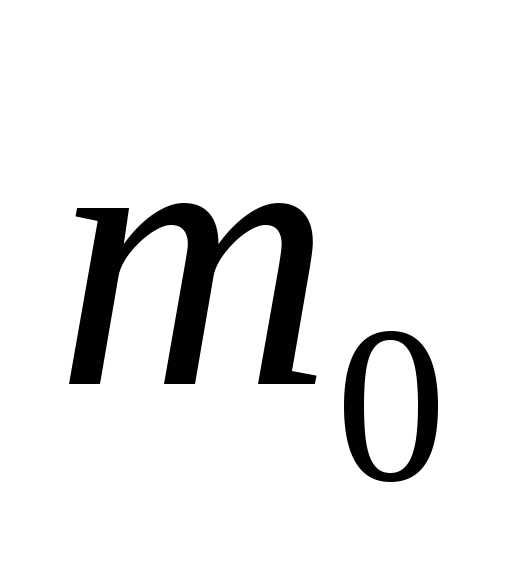
масса молекулы
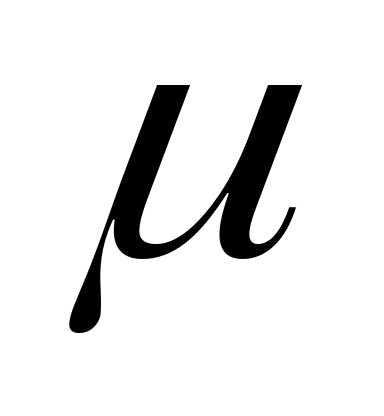
молярная масса
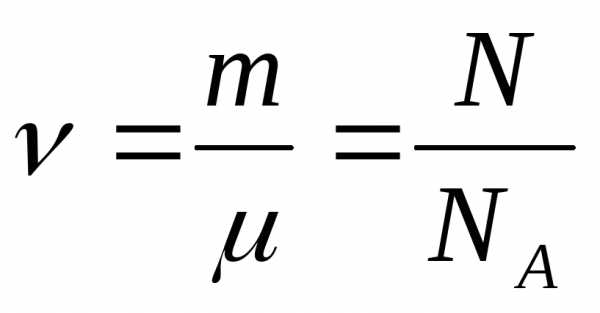
число молекул.
Теплоемкость тела.
с – теплоемкость
тела
U
– внутренняя энергия
А – работа
q –
теплота сгорания
!!! Бывает наоборот!
Линейное расширение
твердых тел.
—
кооф. линейного расширен.
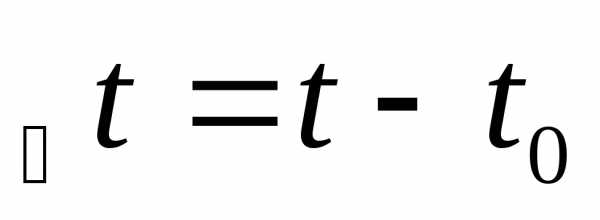
интервал температур.
Объемное расширение
твердых тел.

кооф. объемного расш. тел.
Свойства газов.
T
= const
– изотермический
P
= const
– изобарический
V
= const
– изохорический
Главный газовый
закон:
Закон Менделеева
– Клаперона
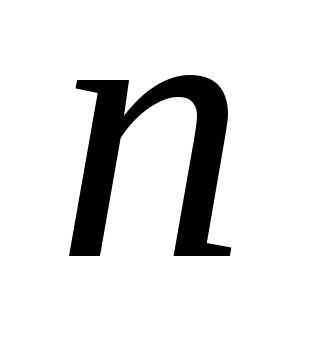
концентрация молекул
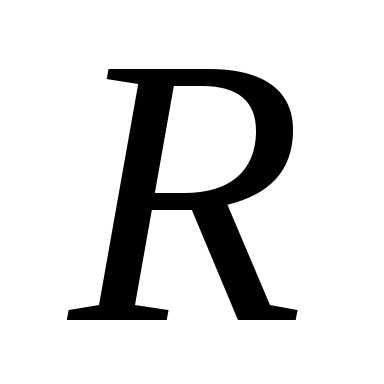
8.31 Дж/моль*К
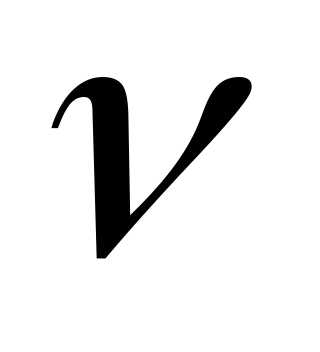
кол-во в-ва.
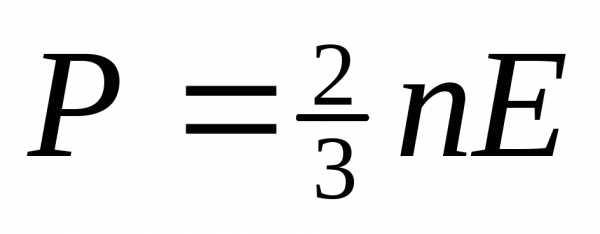

k =
1.38*10^-23 Дж/К
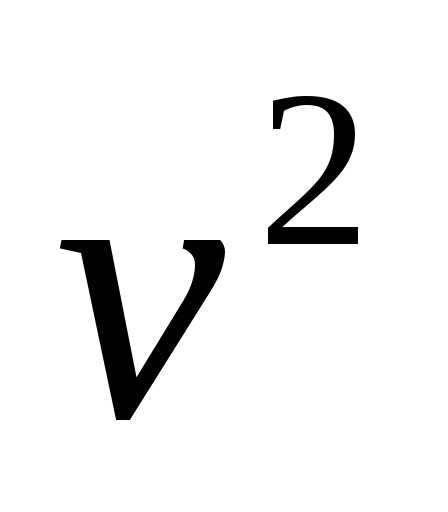
среднеквадратичная ск-ть

средняя кинетич. энергия движ. мол-лы.
КПД тепловой машины.

кол-во теплоты, получ. рабочим телом от
нагрев.
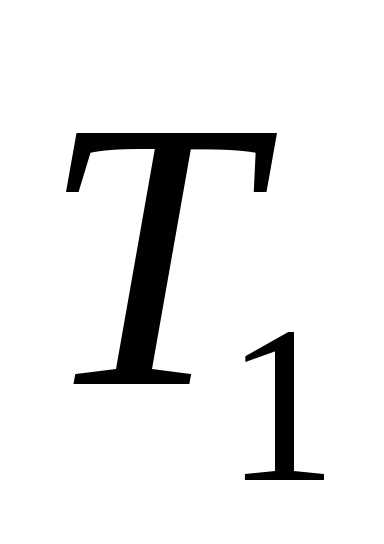
t
холод.
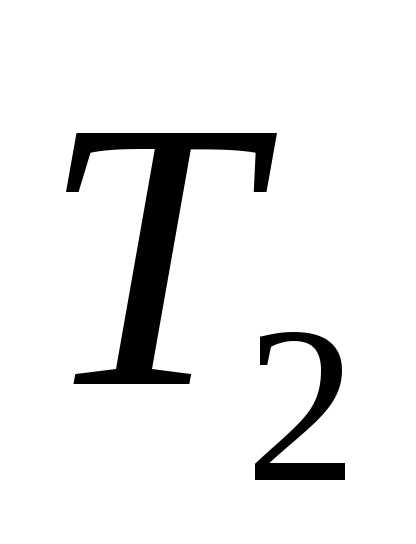
нагреват.
Электричество и
магнетизм.
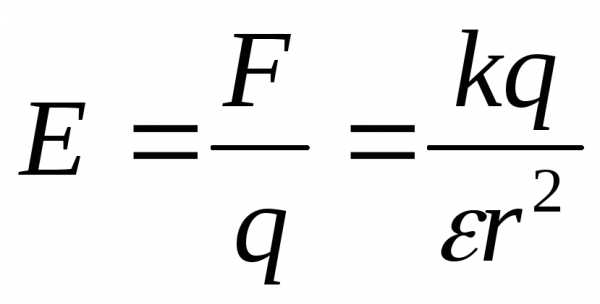
;
Эквипотенциальные
пов-ти.
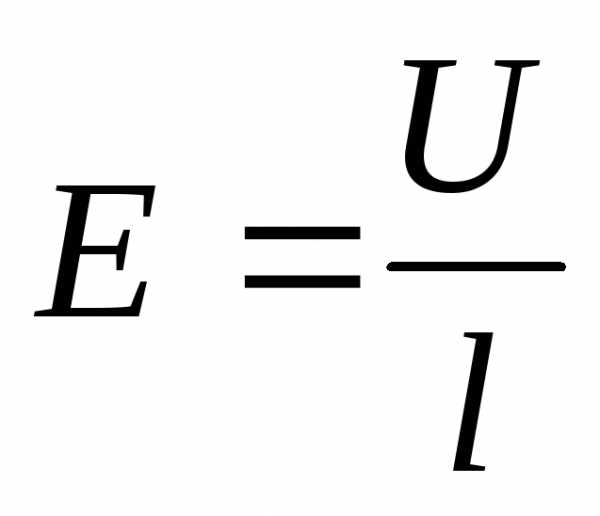
l
– расстояние

поверхностная плотность заряда
Закон Кулона
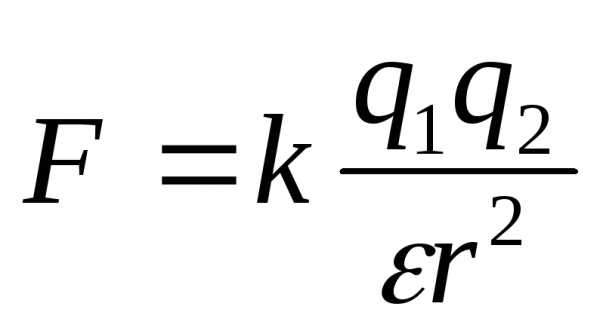
[Н]
Ф/м
эл. постоянная
Электроемкость.
Конденсаторы.
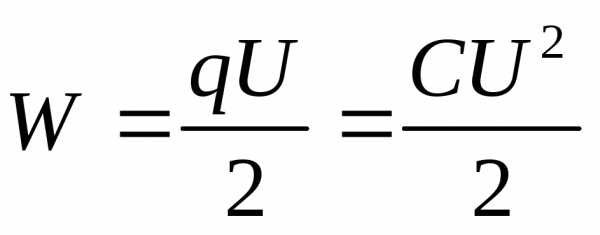
W
– Энергия
Электроемкость
плоского:
Шара:
Параллельное
подключение конденсаторов:
Последовательное
подключение:
Постоянный
электрический ток.

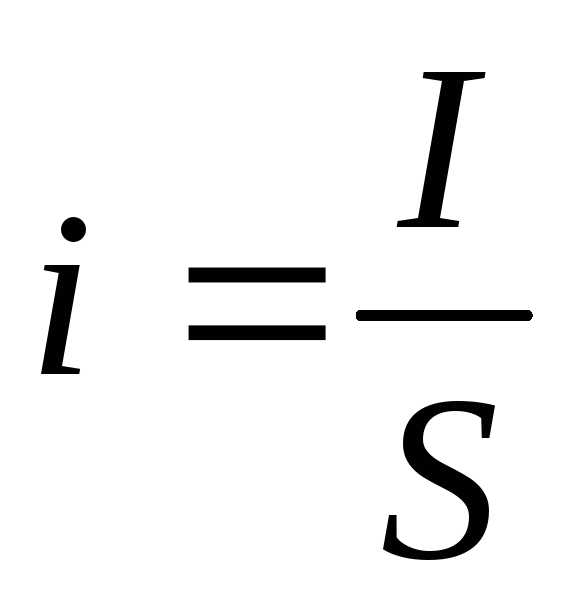
i
– плотность тока
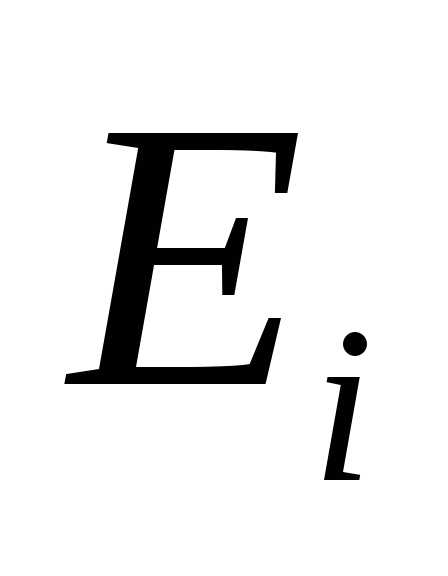
Электродвиж. сила
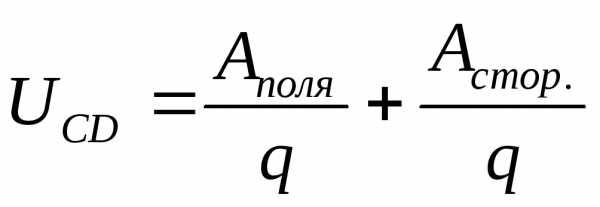

работа, совершенная сторонними силами
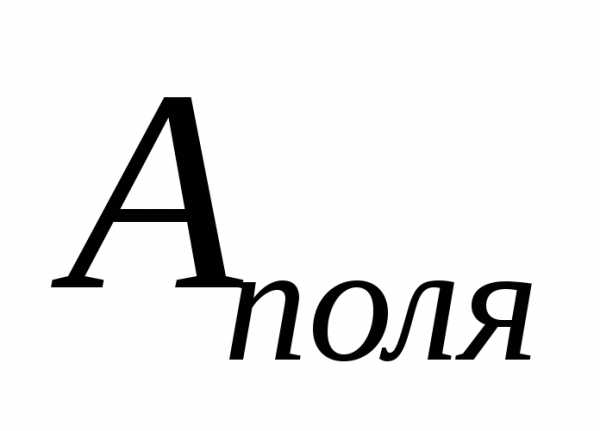
сила эл. поля
Закон Ома для
участка цепи.

G
— кооф. пропрциональности проводника(его
проводимость)
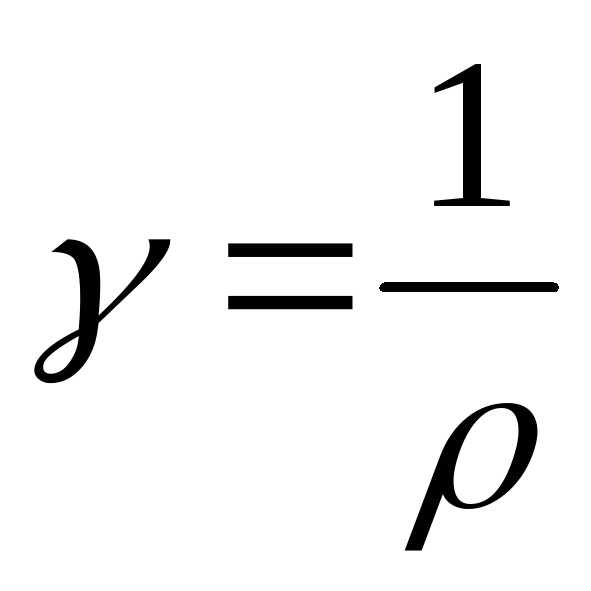

удельная проводимость.

температурный кооф. сопр.

удельное сопротивление
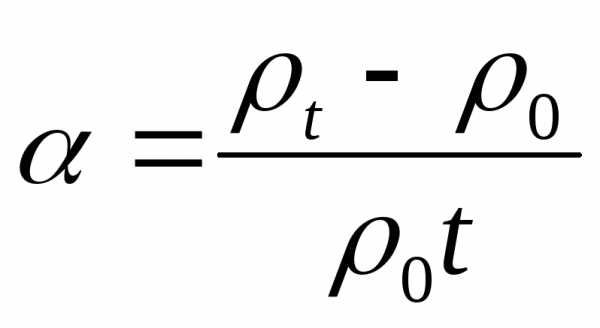
^ -1]
постоянная:
Последовательное
и парал-ное соединение проводников.
Последовательное:
Параллельное:
Закон Ома для полной
цепи:
Последоват. соед.
батарей:
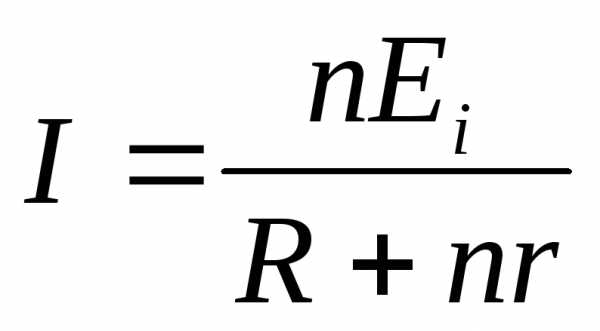
n
– кол-во батарей
Параллельное соед.
батарей:
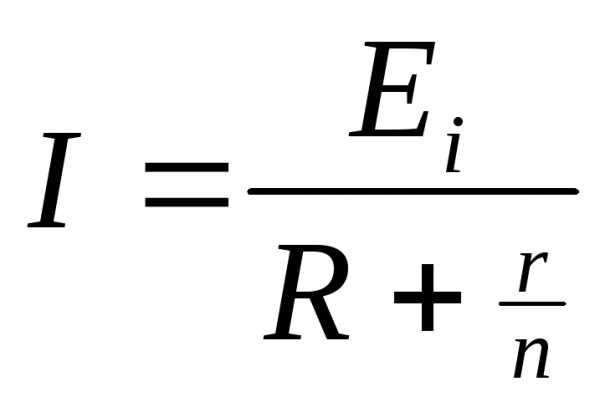
Работа при перемещении
эл. заряда в эл. поле. Потенциал.
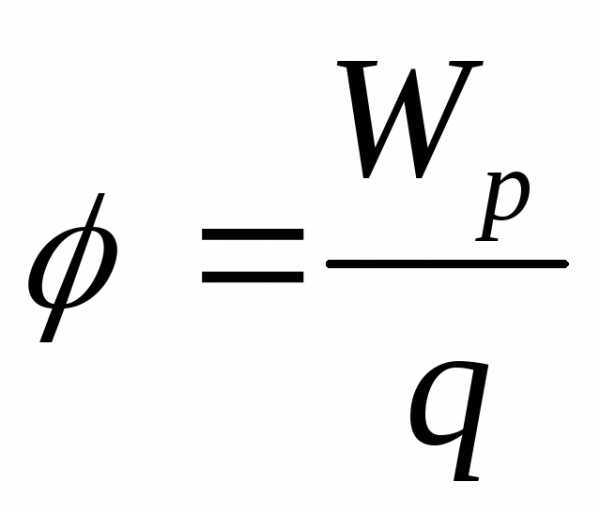

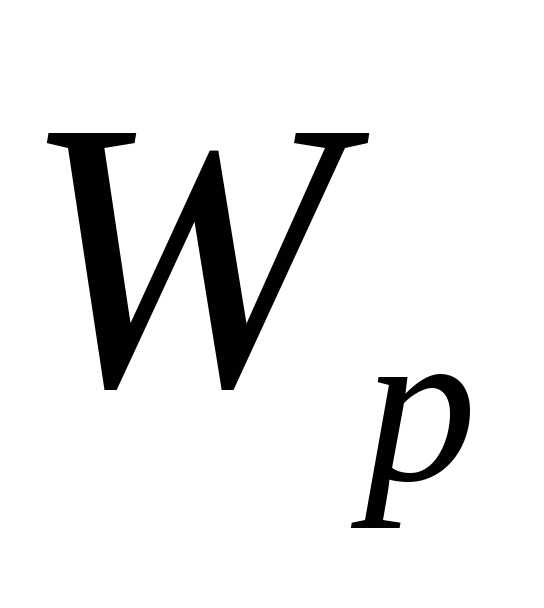
потенциальная энергия заряда в поле.
Работа и мощность
эл. тока:
Напряжение.
Магнитное поле
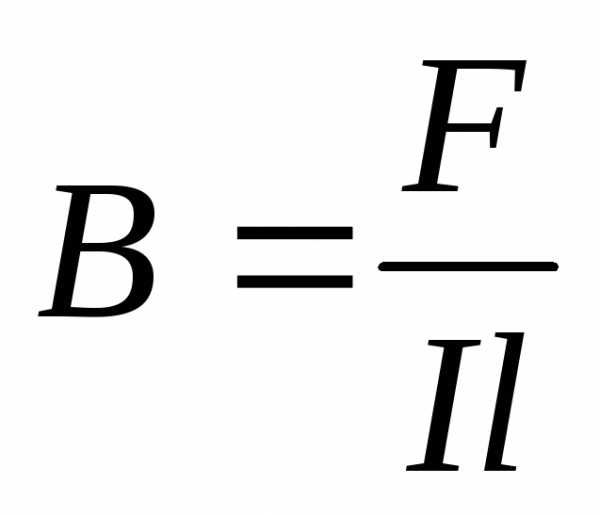
При расположении
проводника с током под углом альфа к
вектору В.
B
– магнитная индукция
I
— сила тока
l
– длинна проводника
M
– макс. момент сил
S
– площадь рамки
Сила Лоуренца

n
– концентр. свободных частиц
v
–скорость упор. движ.
S
–площадь поперечного сечения проводника
Магнитная
прониуаемость.
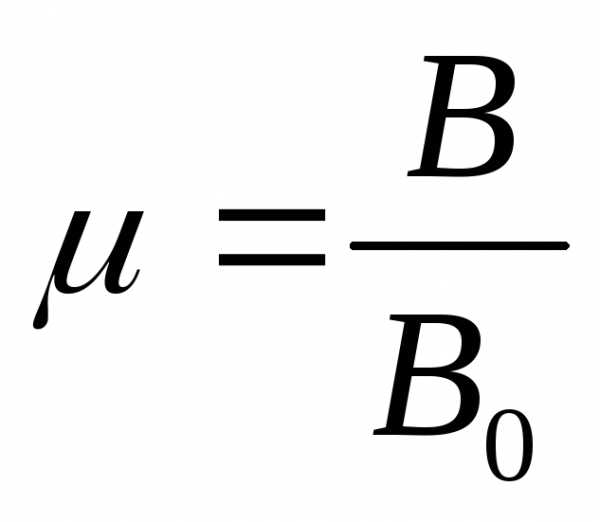
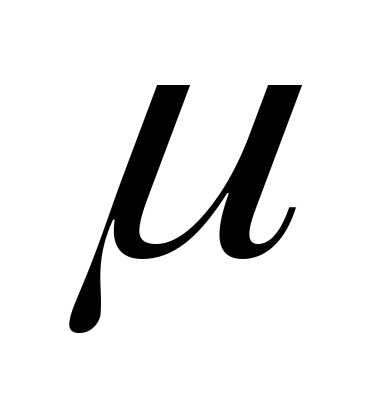
прониц. среды
H-
напряженность магнитного поля.
Электромагнитная
индукция
[Вб]

Ф – магнитный поток
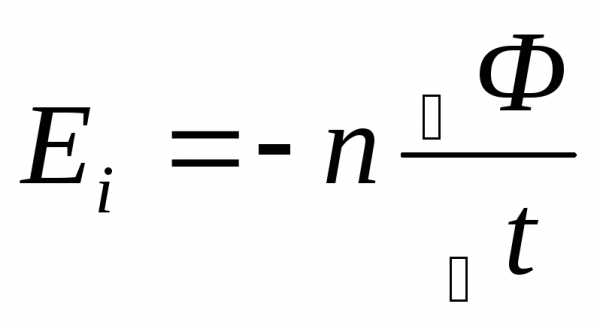
Самоиндукция.
;
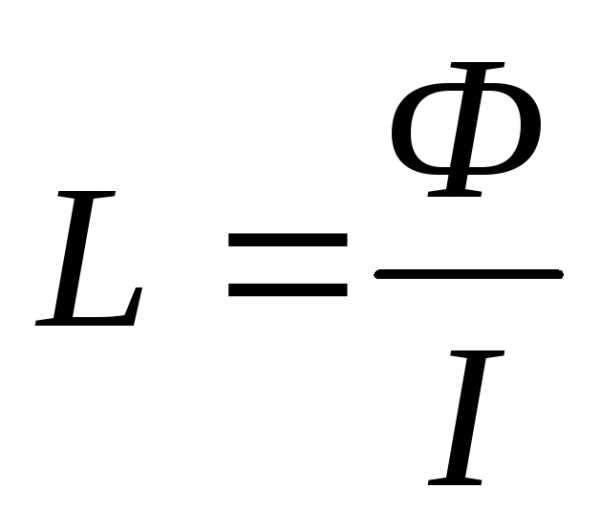
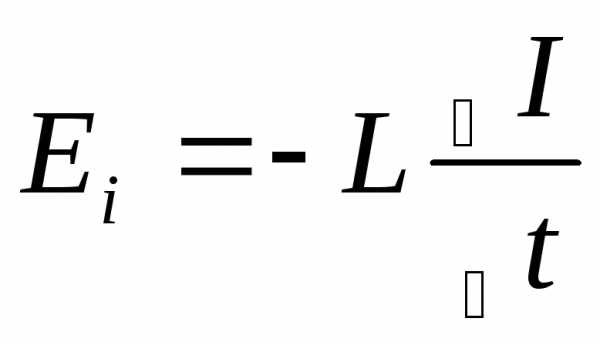
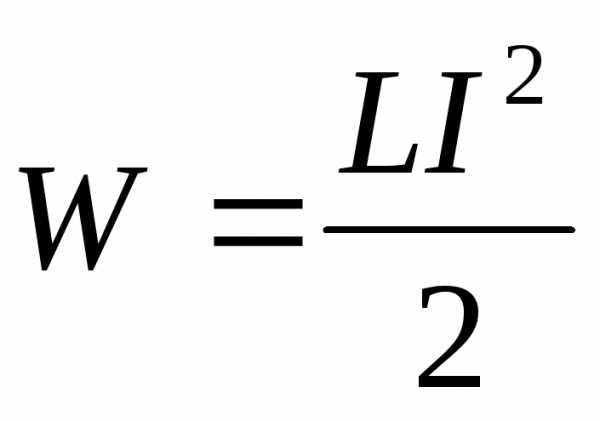
W — энергия
Магнитная рамка.
b,a
– стороны рамки
S
— площадь рамки
Электроны.

Электролиты
Оптика
Закон преломления
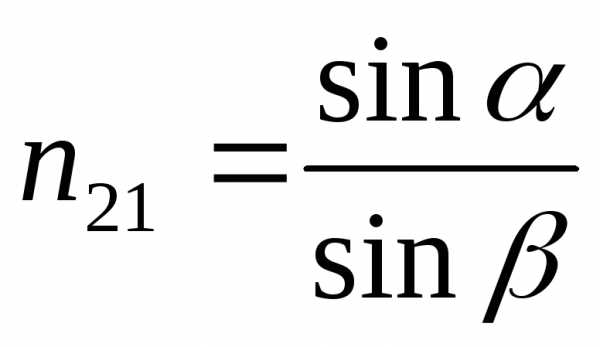
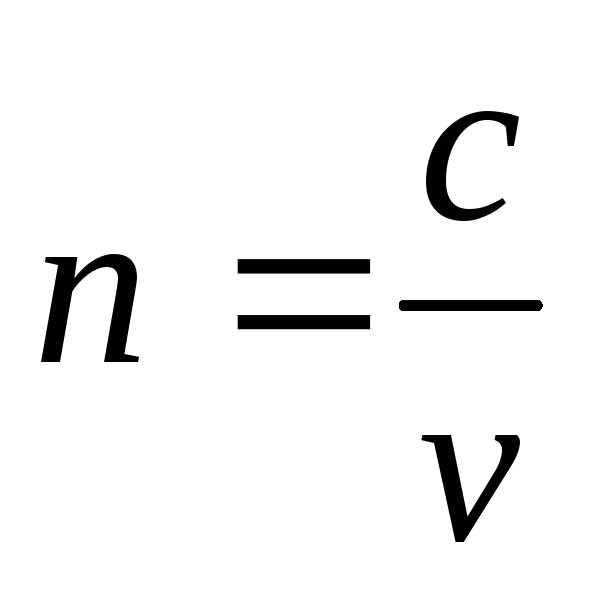
ваакум
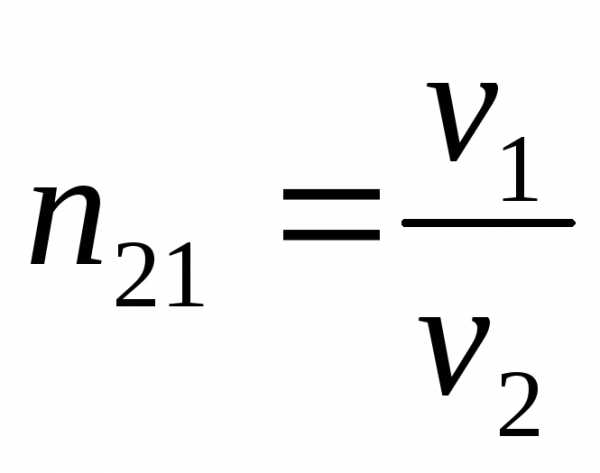
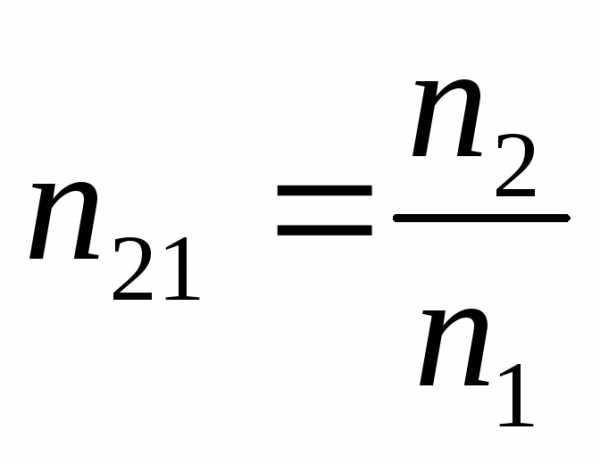


относит. показатель преломления.

скорости света во 2-й и первой средах.
Линзы
d
–расстояние предмета от линзы
f
–расстояние от изображения до предмета
F
– фокус
D
–Оптическая сила линзы [диоптрии]
k
— увеличение линзы
Квантовая физика
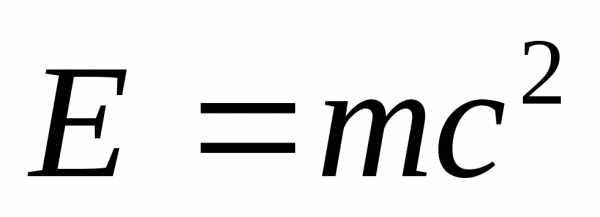
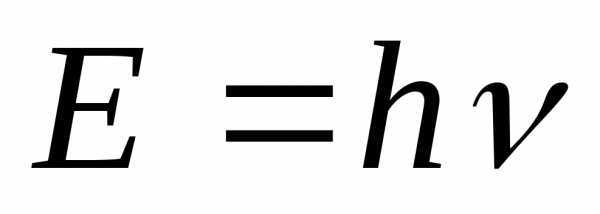
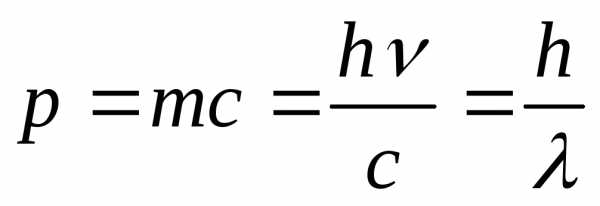

длинна волны излучения
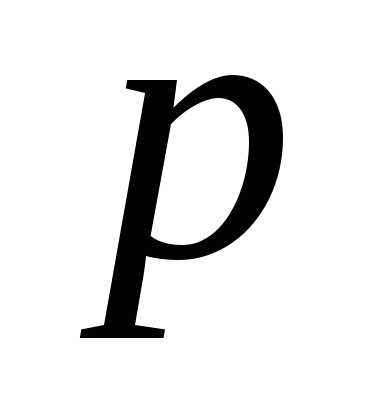
импульс фотона

частота излучения
В магнитно-преломляющих
средах:
В однородно
прозрачной среде:

относит. диэликтрич. проницаемость
среды

относит. магнитная проницаемость среды.
n
– постоянная
Уравнение Эйнштейна.
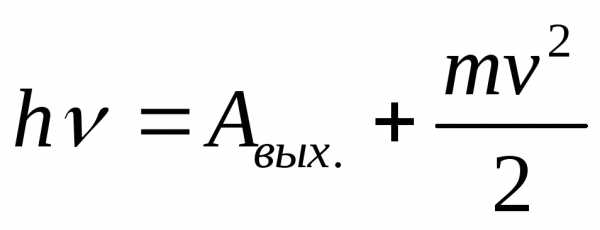
А – работа выхода
электрона из в-ва
Фотоэффект.
Для того, чтобы
фотоэффект имел место, необходимо что
бы энергия кванта света была больше
работы выхода. Предльное значение
частоты, при которой еще наблюдается
фотоэффект, наз. красной границей
фотоэффекта.
studfiles.net
Все формулы по школьной физике
Площади
l – длинна
b — высота,
ширина.
Площадь круга:
Кинематика.
Равномерное движение:
a = 0
V = S/t
Ускоренное движение:
a > 0
a = (V – V0 )/ t
S = S0 + V0t
± (at2
)/2
a = (V2 – V02
)/ 2S
Последовательный ряд нечетных чисел:
— ую:
просто:
Движение под углом к горизонту.
Скорость по оси ОХ:
Скорость по оси ОУ:
Максимальное время подъема:
tполн = 2t
Расстояние :
S = Vx tполн.
Максимальная высота:
Движение тела, брошенного горизонтально:
;
Динамика.
F = ma
P = mg
Fтр. = -mN
F = -F
Момент сил.
M=Fl
M1+M2+…+Mn = 0
Пружина.
x – удлинение.
k – кооф. растяжения.
<l = l – l0
<l – абсолют. удлинение пружины.
ε -относит.
удлинение.
l0 –
начальная длинна
Работа и энергия.
;
;
Движение по окр-ти.
;
w — угловая
скорость.[рад/с]
v -линейная скорость.
n — частота обращения. [об./мин.]
T – период обращения. [время]
Угловая скорость. Период
обращения.
; ;
; ;
Для случаев, когда n = [обороты]
;
— частота [1/с = 1 Гц]
— угол.
l – длинна дуги.
Импульс.
;
Не упругое вз-вие.
до: после:
в проекции на ось х:
Упругое соударение.
до вз-я: после:
в проекции на ось х:
Реактивное движение:
в проекции на ось х: (вверх)
║
0
изначально.
— импульс газов
Импульс силы.
Механика жидкостей и газов.
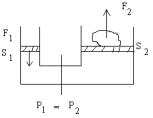
Давление. Закон Паскаля.
-//- жидкости на дно сосуда.
; F – сила давления
S – поверхность[1Па = 1Н/1]
h – высота уровня жидкости.
Сообщающиеся сосуды.
;
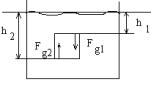
Архимедова сила. Атм. давление
;
;
/
вытесненной жидкости цилиндром.
Закон Гука.
Растягив. сила.
l –первоначальная длинна стержня
Δl –абсолютное удлинение
S –площадь поперечного сеч.
E –кооф. пропорцион., модуль Юнга, модуль упругости.
— напряженность
-закон Гука
КПД машин.
; [1дж/1с = 1 Вт]
Колебания и волны. Звук.
F – возвращающая сила
k – постоянная возвращающ.
x – смещение
Маятник.
;l – длинна маятника
Математический маятник – точка, подвешенная на
невесомой и нерастяжимой нити.
Пружинный маятник:
;
— циклическая частота колебаний
Фаза колебаний.
— угловая скорость
— угол поворота
Скорость распространения волн
;
Электромагнитные колебания.
;
— собственна частота колебаний в контуре
;
;
— фаза колебаний
— амплитуда тока
С – скорость в ваакуме
n – абс. показатель преломления среды
Молекулярно-кинетическая
теория
;
— масса молекулы
— молярная масса
; N – число
молекул.
Теплоемкость тела.
с – теплоемкость тела
U – внутренняя энергия
А – работа
q – теплота сгорания
!!! Бывает наоборот!
Линейное
расширение твердых тел.
— кооф. линейного расширен.
— интервал температур.
Объемное
расширение твердых тел.
— кооф. объемного расш. тел.
Свойства газов.
T = const –
изотермический
P = const – изобарический
V = const –
изохорический
Главный газовый закон:
Закон Менделеева – Клаперона
— концентрация молекул
= 8.31 Дж/моль*К
— кол-во в-ва.
;
;
k = 1.38*10^-23 Дж/К
— среднеквадратичная ск-ть
— средняя кинетич. энергия движ. мол-лы.
КПД тепловой машины.
— кол-во теплоты, получ. рабочим телом от нагрев.
— t холод.
— нагреват.
Электричество и магнетизм.
[В/м] ;
Эквипотенциальные пов-ти.
;
l – расстояние
— поверхностная плотность заряда
Закон Кулона
; [Н]
Ф/м
эл.
постоянная
Электроемкость. Конденсаторы.
[Дж]
W – Энергия
Электроемкость плоского:
Шара:
Параллельное подключение конденсаторов:
Последовательное подключение:
Постоянный электрический ток.
;
; i – плотность тока
— Электродвиж. сила
[В]
— работа, совершенная сторонними силами
— сила эл. поля
Закон Ома для участка цепи.
;
G — кооф.
пропрциональности проводника(его проводимость)
;
— удельная проводимость.
— температурный кооф. сопр.
— удельное
сопротивление
[1 град. ^ -1]
постоянная:
Последовательное
и парал-ное соединение проводников.
Последовательное:
Параллельное:
Закон Ома для полной цепи:
Последоват. соед. батарей:
;
n – кол-во батарей
Параллельное соед. батарей:
;
Работа при перемещении эл. заряда в эл. поле.
Потенциал.
;
— потенциал эл. поля
— потенциальная энергия заряда в поле.
Работа и мощность эл. тока:
Напряжение.
Магнитное поле
;
При расположении проводника с током под углом альфа к
вектору В.
B – магнитная индукция
I — сила тока
l – длинна проводника
M – макс. момент сил
S – площадь
рамки
Сила Лоуренца
;
n – концентр. свободных частиц
v –скорость упор. движ.
S –площадь поперечного сечения проводника
Магнитная прониуаемость.
;
— магнитная прониц. среды
H- напряженность магнитного поля.
Электромагнитная индукция
[Вб]
;
Ф – магнитный поток
;
Самоиндукция.
; [Гн]
;
; W — энергия
Магнитная
рамка.
b,a – стороны
рамки
S — площадь
рамки
Электроны.
;
Электролиты
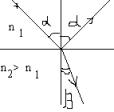
Оптика
Закон преломления
; — ваакум
; ; ;
— относит. показатель преломления.
— скорости света во 2-й и первой средах.
Линзы
d –расстояние предмета от линзы
f –расстояние от изображения до предмета
F – фокус
D –Оптическая сила линзы [диоптрии]
k — увеличение
линзы
Квантовая физика
; ;
;
— длинна волны излучения
— импульс фотона
— частота излучения
В магнитно-преломляющих средах:
В однородно прозрачной среде:
— относит. диэликтрич. проницаемость среды
— относит. магнитная проницаемость среды.
n – постоянная
Уравнение Эйнштейна.
;
А – работа выхода электрона из в-ва
Фотоэффект.
Для того, чтобы фотоэффект имел место, необходимо что
бы энергия кванта света была больше работы выхода. Предельное значение частоты,
при которой еще наблюдается фотоэффект, наз. красной границей фотоэффекта.
Список литературы
Для подготовки данной работы были использованы
материалы с сайта http://ilib.ru/
Дата добавления: 30.07.2003
www.km.ru
Площади фигур — формулы.
2014-07-25 | Автор: Анна
Вспоминаем формулы для вычисления площадей фигур!
Формулы площадей фигур
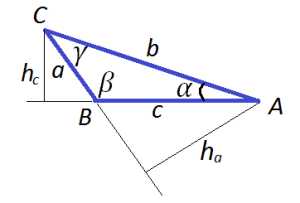
| Треугольник общего вида. a, b, c — стороны, p — полупериметр, r — радиус вписанной окружности, R — радиус описанной окружности |
 |
|
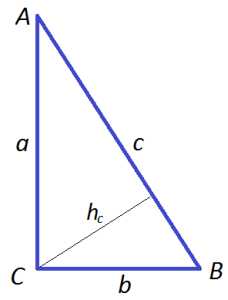
| Прямоугольный треугольник. a, b — катеты, с — гипотенуза, p — полупериметр, r — радиус вписанной окружности, R — радиус описанной окружности |
 |
 |
| Правильный треугольник |
 |
|
| Прямоугольник. a,b — стороны, d — диагонали. |
||
| Квадрат. | 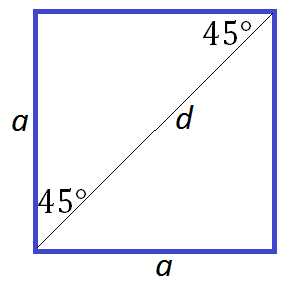 |
|
| Параллелограмм. a,b — стороны, d — диагонали, h — высота |
||
| Ромб. a — сторона, d — диагональ, h — высота |
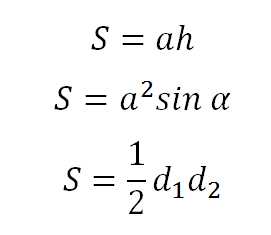 |
|
| Трапеция. a,b — основания, h — высота, d — диагонали. |
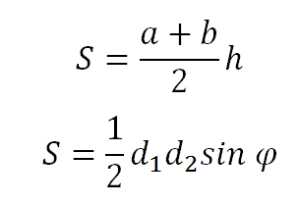 |
|
| Круг. |  |
|
| Элементы круга. | 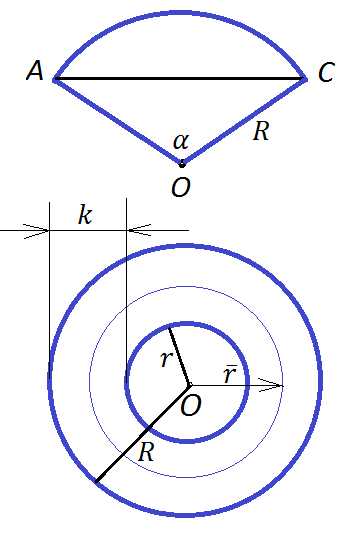 |
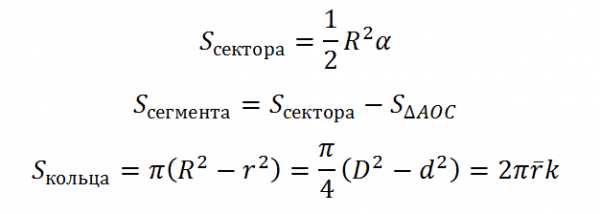 |
| Правильный n-угольник |
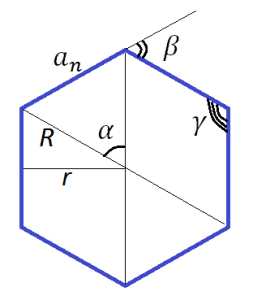 |
easy-physic.ru
Содержание:
Определение площади и объема:
В повседневной жизни нам довольно часто приходится иметь дело с определением таких величин, как площадь и объем. Представьте себе, что вам необходимо сделать ремонт в квартире (или доме): побелить стены и потолок, покрасить пол. Чтобы закупить необходимое количество материалов, нужно определить площадь поверхностей и объем краски.
Из уроков математики вам известно, как находить площадь некоторых фи-гур: квадрата, прямоугольника, параллелограмма.
|
Рис. 6.1. |
Рис. 6.2. |
Рис. 6.3 |
Площадь прямоугольника ABCD (рис. 6.1) вычисляется по формуле:
S = a · b, (6.1)
где a – ширина прямоугольника, b – высота.
Площадь параллелограмма ABCD (рис. 6.2) также находится по формуле 6.1. Площадь квадрата найти легко, поскольку его ширина и высота одинаковы:
S = a · a = a2 , (6.2)
Из рис. 6.1 видно, что площадь прямоугольного треугольника АBC можно найти по формуле:
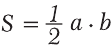
Проблема определения площади круга была решена еще в Древней Греции. Для этого нужно знать радиус круга и число «пи», приблизительное значение
которого π ≈ 3,14.
Площадь круга равняется
S = π · R2, (6.4) .
Значение числа 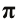
Вычисление объема простых фигур
Каждое тело занимает определенный объем. Чем большую часть пространства занимает тело, тем больше его объем. Объем обозначают буквой V (от volume – объем). Чтобы найти объем прямоугольного бруска или ящика (математики называют эту геометрическую фигуру параллелепипедом) со сторона-ми a, b и h, надо их перемножить (рис. 6.4):
|
Рис. 6.4. |
Рис. 6.5. |
|
V = a · b · h (6.4)
Поскольку S = a · b,
где S – это площадь основания ящика, то формулу (6.4) можно переписать и так:
V = S · h (6.5)
У куба все ребра равны, потому его объем равняется:
V = a · a · a = a3 (6.6)
Объем цилиндра (рис. 6.5) с радиусом основания R и высотой h можно также определить по формуле (6.5), то есть:
V = S · h = πR2 · h (6.7)
Объем шара (рис. 6.6)
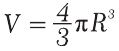
Единицы измерения объема
Поскольку длину сторон измеряют в единицах длины (метр, дециметр, сантиметр и т. д.), то единицы измерения объема – это единицы длины, возведенные в третью степень.
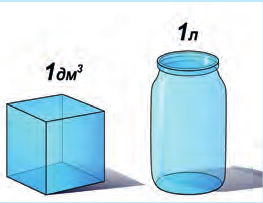
Куб с ребром 1 м имеет объем 1 м3 (один кубический метр). Один литр (1 л) по определению – это объем куба с ребром 1 дм (рис. 6.7), то есть 1 л = 1 дм3 (дециметр кубический). Один литр равен 1000 кубических сантиметров: 1 л = 1000 см3. Объем в один сантиметр кубический еще называют миллилитром, то есть тысячной частью литра (1 мл = 0,001 л).
Рис. 6.7. Один литр – это 1дм3
Напомним, что дециметр – это десятая часть метра, а сантиметр – сотая часть метра
Таблица 6.1
| 1 м3 = 1 000 л | 1 м3 = 1 000 000 см3 |
| 1 л = 1 дм3 | 1 л = 1000 см3 |
| 1 дм3 = 1 000 см3 | 1 л = 1 000 мл |
| 1 см3 = 1 мл | 1 мл = 0,001 л |
- Заказать решение задач по физике
Измерение объема тел неправильной формы
Прибор для измерения объема называют мензуркой, или мерным цилиндром (рис. 6.8). Мензурка – это прозрачный сосуд с нанесенными делениями, которые обозначают объем в миллилитрах. Дома у вас наверняка есть мерный стакан, то есть та же мензурка. Литровой или поллитровой банкой, или стаканом (250 мл) также можно пользоваться, если не нужна большая точность. С помощью мензурки можно определить объем жидкости и тела неправильной формы. Для этого в мензурку нужно налить воду и определить объем этой воды. Потом полностью погрузить тело в воду и запомнить новое значение объема. Разница измеренных значений равна объему тела.
Рис. 6.8. Деления мензурки определяют объем в миллилитрах (то есть в см3)
История:
 |
Существует легенда, согласно которой первым такой способ определения объема изобрел древнегреческий ученый Архимед. Произошло это во время размышлений над довольно сложной зада-чей, предложенной царем Гиероном. Идея решения возникла тогда, когда Архимед влез в ванну и заметил, что уровень воды поднялся. Ученый понял, что вытесненный объем воды как раз равен объему погруженного в нее тела. Восторженный Архимед выпрыгнул из ванны и выбежал на улицу с криком «Эврика! Эврика!», что в переводе с древнегреческого значит «На-шел! Нашел!». |
Итоги:
- Площадь тел правильной формы равна произведению основы на высоту и измеряется в квадратных единицах длины S = a · b.
- Объем тел правильной формы определяется как произведение площади основы на высоту и измеряется в кубических единицах V = S · h.
- Объем тел произвольной формы определяют с помощью мензурки
- Площадь круга определяют по формуле S = π · R2.
- Объем шара равен
.
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Что изучает механика в физике
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
- Точность измерений и погрешности
Все формулы по школьной физике
Площади
l – длинна
b — высота,
ширина.
Площадь круга:
Кинематика.
Равномерное движение:
a = 0
V = S/t
Ускоренное движение:
a > 0
a = (V – V0 )/ t
S = S0 + V0t
± (at2
)/2
a = (V2 – V02
)/ 2S
Последовательный ряд нечетных чисел:
— ую:
просто:
Движение под углом к горизонту.
Скорость по оси ОХ:
Скорость по оси ОУ:
Максимальное время подъема:
tполн = 2t
Расстояние :
S = Vx tполн.
Максимальная высота:
Движение тела, брошенного горизонтально:
;
Динамика.
F = ma
P = mg
Fтр. = -mN
F = -F
Момент сил.
M=Fl
M1+M2+…+Mn = 0
Пружина.
x – удлинение.
k – кооф. растяжения.
<l = l – l0
<l – абсолют. удлинение пружины.
ε -относит.
удлинение.
l0 –
начальная длинна
Сила всемирного тяготения
Сила тяжести
Работа и энергия.
;
;
Криволинейное движение
Движение по окр-ти.
;
w — угловая
скорость.[рад/с]
v -линейная скорость.
n — частота обращения. [об./мин.]
T – период обращения. [время]
Угловая скорость. Период
обращения.
;
;
;
;
Для случаев, когда n = [обороты]
;
— частота [1/с = 1 Гц]
— угол.
l – длинна дуги.
Импульс.
;
Не упругое вз-вие.
до: после:
в проекции на ось х:
Упругое соударение.
до вз-я: после:
в проекции на ось х:
Реактивное движение:
в проекции на ось х: (вверх)
║
0
изначально.
— импульс газов
Импульс силы.
Механика жидкостей и газов.
Давление. Закон Паскаля.
-//- жидкости на дно сосуда.
; F – сила давления
S – поверхность[1Па = 1Н/1]
h – высота уровня жидкости.
Сообщающиеся сосуды.
;
Архимедова сила. Атм. давление
;
;
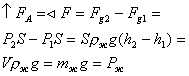
вытесненной жидкости цилиндром.
Закон Гука.
Растягив. сила.
l –первоначальная длинна стержня
Δl –абсолютное удлинение
S –площадь поперечного сеч.
E –кооф. пропорцион., модуль Юнга, модуль упругости.
— напряженность
-закон Гука
КПД машин.
; [1дж/1с = 1 Вт]
Колебания и волны. Звук.
F – возвращающая сила
k – постоянная возвращающ.
x – смещение
Маятник.
;l – длинна маятника
Математический маятник – точка, подвешенная на
невесомой и нерастяжимой нити.
Пружинный маятник:
;
— циклическая частота колебаний
Фаза колебаний.
— угловая скорость
— угол поворота
Скорость распространения волн
;
Электромагнитные колебания.
;
— собственна частота колебаний в контуре
;
;
— фаза колебаний
— амплитуда тока
С – скорость в ваакуме
n – абс. показатель преломления среды
Молекулярно-кинетическая
теория
;
— масса молекулы
— молярная масса
; N – число
молекул.
Теплоемкость тела.
с – теплоемкость тела
U – внутренняя энергия
А – работа
q – теплота сгорания
!!! Бывает наоборот!
Линейное
расширение твердых тел.
— кооф. линейного расширен.
— интервал температур.
Объемное
расширение твердых тел.
— кооф. объемного расш. тел.
Свойства газов.
T = const –
изотермический
P = const – изобарический
V = const –
изохорический
Главный газовый закон:
Закон Менделеева – Клаперона
— концентрация молекул
= 8.31 Дж/моль*К
— кол-во в-ва.
;
;
k = 1.38*10^-23 Дж/К
— среднеквадратичная ск-ть
— средняя кинетич. энергия движ. мол-лы.
КПД тепловой машины.
— кол-во теплоты, получ. рабочим телом от нагрев.
— t холод.
— нагреват.
Электричество и магнетизм.
[В/м] ;
Эквипотенциальные пов-ти.
;
l – расстояние
— поверхностная плотность заряда
Закон Кулона
; [Н]
Ф/м
эл.
постоянная
Электроемкость. Конденсаторы.
[Дж]
W – Энергия
Электроемкость плоского:
Шара:
Параллельное подключение конденсаторов:
Последовательное подключение:
Постоянный электрический ток.
;
; i – плотность тока
— Электродвиж. сила
[В]
— работа, совершенная сторонними силами
— сила эл. поля
Закон Ома для участка цепи.
;
G — кооф.
пропрциональности проводника(его проводимость)
;
— удельная проводимость.
— температурный кооф. сопр.
— удельное
сопротивление
[1 град. ^ -1]
постоянная:
Последовательное
и парал-ное соединение проводников.
Последовательное:
Параллельное:
Закон Ома для полной цепи:
Последоват. соед. батарей:
;
n – кол-во батарей
Параллельное соед. батарей:
;
Работа при перемещении эл. заряда в эл. поле.
Потенциал.
;
— потенциал эл. поля
— потенциальная энергия заряда в поле.
Работа и мощность эл. тока:
Напряжение.
Магнитное поле
;
При расположении проводника с током под углом альфа к
вектору В.
B – магнитная индукция
I — сила тока
l – длинна проводника
M – макс. момент сил
S – площадь
рамки
Сила Лоуренца
;
n – концентр. свободных частиц
v –скорость упор. движ.
S –площадь поперечного сечения проводника
Магнитная прониуаемость.
;
— магнитная прониц. среды
H- напряженность магнитного поля.
Электромагнитная индукция
[Вб]
;
Ф – магнитный поток
;
Самоиндукция.
;
[Гн]
;
; W — энергия
Магнитная
рамка.
b,a – стороны
рамки
S — площадь
рамки
Электроны.
;
Электролиты
Оптика
Закон преломления
;
— ваакум
;
;
;
— относит. показатель преломления.
— скорости света во 2-й и первой средах.
Линзы
d –расстояние предмета от линзы
f –расстояние от изображения до предмета
F – фокус
D –Оптическая сила линзы [диоптрии]
k — увеличение
линзы
Квантовая физика
;
;
;
— длинна волны излучения
— импульс фотона
— частота излучения
В магнитно-преломляющих средах:
В однородно прозрачной среде:
— относит. диэликтрич. проницаемость среды
— относит. магнитная проницаемость среды.
n – постоянная
Уравнение Эйнштейна.
;
А – работа выхода электрона из в-ва
Фотоэффект.
Для того, чтобы фотоэффект имел место, необходимо что
бы энергия кванта света была больше работы выхода. Предельное значение частоты,
при которой еще наблюдается фотоэффект, наз. красной границей фотоэффекта.
Список литературы
Для подготовки данной работы были использованы
материалы с сайта http://ilib.ru/
Дата добавления: 30.07.2003
База рефератов на портале KM.RU существует с 1999 года. Она пополнялась не только готовыми рефератами, докладами, курсовыми, но и авторскими публикациями, чтобы учащиеся могли использовать их и цитировать при самостоятельном написании работ.
Это популяризирует авторские исследования и научные изыскания, что и является целью работы истинного ученого или публициста. Таким образом, наша база — электронная библиотека, созданная в помощь студентам и школьникам.
Уважаемые авторы! Если Вы все же возражаете против размещения Вашей публикации или хотите внести коррективы, напишите нам на почту info@corp.km.ru, мы незамедлительно выполним Вашу просьбу или требование.
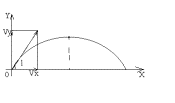
По графику скорости от времени v(t) можно найти перемещение тела. Для этого нужно уметь рассчитывать площади плоских фигур.
По-английски «Square» – значит «площадь». Первая буква этого слова – буква «S». Перемещение обозначают буквой S потому, что S – это площадь фигуры, заключенной между линией скорости и горизонтальной осью времени.
Как вычислить площади плоских фигур
Рис.1. Чтобы рассчитать перемещение по графику v(t) нужно уметь вычислять площади трех плоских фигур
Площадь прямоугольника
Площадь прямоугольника (рис. 1а) можно найти, перемножив две его перпендикулярные стороны:
[ large boxed{ S_{text{прямоуг}} = a cdot b }]
Площадь трапеции
Примечание: Трапеция – это четырехугольник, две его стороны параллельные, а две другие – не параллельные. Параллельные стороны называются основаниями трапеции.
Умножив полусумму оснований трапеции на ее высоту, получим площадь (рис. 1б) трапеции:
[ large boxed{ S_{text{трапец}} = frac{1}{2} (a + b) cdot h }]
Площадь прямоугольного треугольника
Для прямоугольного треугольника (рис. 1в) площадь можно вычислить, перемножив два его катета и взяв половину от получившегося произведения:
[ large boxed{ S_{text{треуг}} = frac{1}{2} cdot a cdot b }]
Скорость не меняется
Пусть тело движется по прямой и при этом его скорость не изменяется (остается одной и той же). На языке математики «скорость не изменяется» можно записать так:
[v=const]
На графике для скорости v(t) такая скорость обозначается горизонтальной линией. На рисунке 2 эта линия обозначена синим цветом.
Рис.2. Площадь прямоугольника на графике v(t), если скорость тела не изменяется, будет численно равна перемещению тела
Примечание: Движение с постоянной (т. е. с одной и той же) скоростью называют равномерным движением.
Если скорость направлена по оси движения – линия лежит выше оси t времени (рис. 2а).
А когда скорость направлена против оси движения – линия скорости располагается ниже оси t времени (рис. 2б). Математики в таком случае говорят: «Скорость имеет отрицательную проекцию на ось».
Какую бы проекцию не имела скорость – положительную, или отрицательную, длина вектора скорости остается положительной. Поэтому, когда мы вычисляем площадь фигуры, то не учитываем знак «минус» для скорости (рис. 2б).
В обоих случаях перемещение тела можно вычислить по формуле:
[ large S = v_{0} cdot (t_{2} — t_{1}) ]
Примечание: Перемещение тела – это всегда либо нулевая, либо положительная величина S. Математики словосочетание «либо нулевая, либо положительная» заменят одним словом «не отрицательная».
Скорость увеличивается
Когда скорость тела увеличивается, то линия скорости на графике v(t) всегда располагается так, чтобы с ростом времени удаляться от оси времени. Чем больше времени пройдет, тем дальше от горизонтали располагаются точки, лежащие на линии скорости (рис. 3).
Рис.3. Так выглядит зависимость скорости от времени v(t), когда тело увеличивает свою скорость, двигаясь по оси – рис а) и против оси – рис. б)
Примечание: Движение с возрастающей скоростью называют равноускоренным движением.
Когда тело движется по направлению оси, линия скорости расположена выше горизонтальной оси времени (рис 3а).
А если тело движется против оси, линия скорости располагается ниже горизонтальной оси времени (рис. 3б).
Вычислим перемещение тела, движущегося в положительном направлении оси Ox. Для тела, движущегося противоположно оси, перемещение рассчитывается аналогично.
Выбор интервала времени влияет на то, будем ли мы вычислять площадь трапеции (рис. 4а), или прямоугольного треугольника (рис. 4б).
Рис.4. График v(t) — тело движется в положительном направлении оси и увеличивает свою скорость. От того, какой интервал времени мы выберем, зависит, будем ли мы вычислять путь, пройденный телом, с помощью площади трапеции – рис. а), или прямоугольного треугольника — рис. б)
На графике скорости v(t) для рисунка 4а перемещение с помощью трапеции вычисляется так:
[ large S = frac{1}{2} cdot (v_{1} + v_{2}) cdot (t_{2} — t_{1}) ]
А для рисунка 4б перемещение тела найдем с помощью площади треугольника:
[ large S = frac{1}{2} cdot v_{2} cdot (t_{2} — 0) ]
Скорость уменьшается
Когда тело замедляется и его скорость уменьшается, с ростом времени линия скорости приближается к горизонтальной оси t
- сверху – если тело движется по оси (рис. 5а),
- или снизу – когда тело движется против оси (рис. 5б).
Рис.5. Так выглядит зависимость скорости от времени v(t), когда тело уменьшает свою скорость, двигаясь по оси – рис а) и против оси – рис. б)
Примечание: Движение с уменьшающейся по модулю скоростью называют равнозамедленным движением.
Будем вычислять перемещение тела, движущегося в положительном направлении оси Ox. Аналогичным способом рассчитывается перемещение тела, движущегося противоположно оси.
От того, какой интервал времени нас интересует, зависит, будем ли мы вычислять площадь трапеции (рис. 6а), или треугольника (рис. 6б).
Рис.6. График v(t) — тело движется в положительном направлении оси и уменьшает свою скорость. Выбор интервала времени определяет, будем ли мы вычислять путь, пройденный телом, с помощью трапеции – рис. а), или треугольника — рис. б)
Найдем на графике v(t) перемещение с помощью площади трапеции для рисунка 6а:
[ large S = frac{1}{2} cdot (v_{1} + v_{2}) cdot (t_{2} — t_{1}) ]
А для рисунка 6б перемещение тела найдем с помощью площади треугольника:
[ large S = frac{1}{2} cdot v_{1} cdot (t_{2} — t_{1}) ]
Выводы
На графике v(t) перемещение – это:
- площадь прямоугольника, когда скорость не изменяется;
- площадь треугольника, или трапеции, когда скорость изменяется — падает, или растет.
На этой странице представлена справочная информация с формулами для вычисления площадей простых фигур (сечений) с указанием положения их центров тяжестей.
Эта страничка будет полезна при расчёте более сложных фигур (составных поперечных сечений): определении положения центра тяжести, а также общей площади.
Центры тяжести
Для всех фигур, положение центра тяжести в статье обозначается буквой – C, это наиболее используемый вариант. Также иногда центр тяжести обозначают буквой – O.
Формулы для расчёта площадей
В сопромате площадь поперечного сечения обозначается буквой – A, однако, в некоторой литературе ты можешь встретить обозначения с буквой – F.
Другую справочную информацию, размещённую на сайте – ssopromat.ru, можешь найти, перейдя по указанной ссылке.


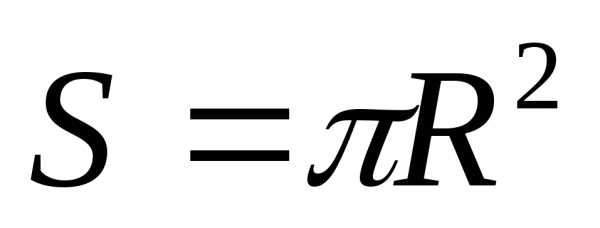


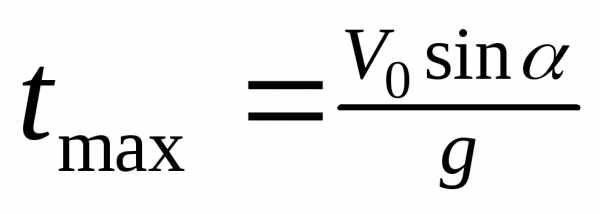
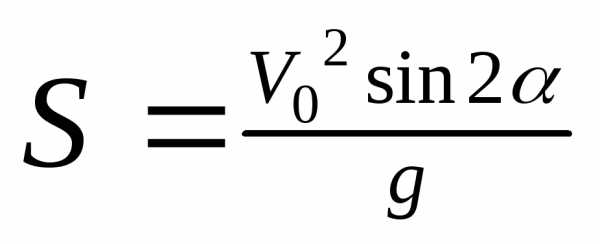
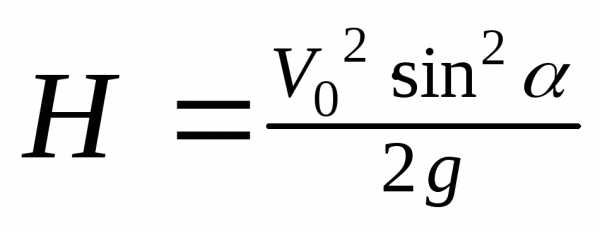

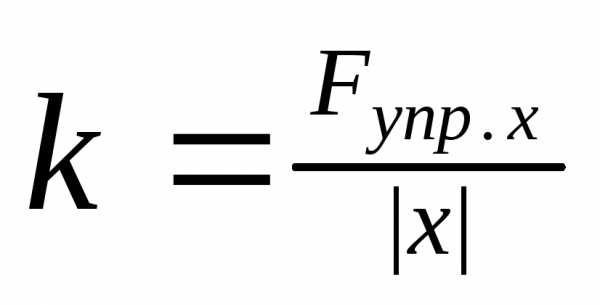
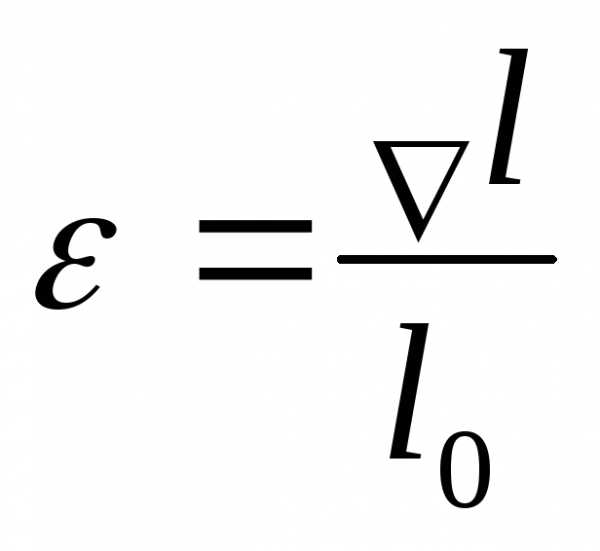

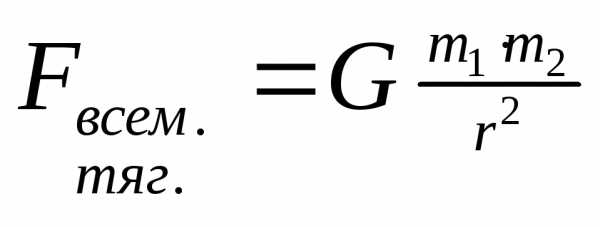
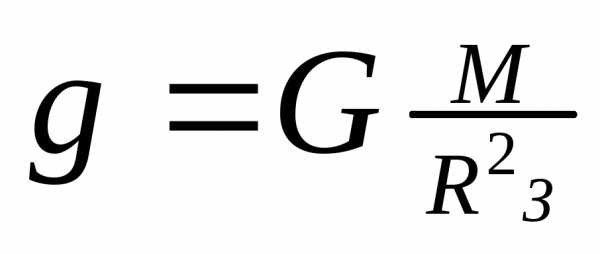
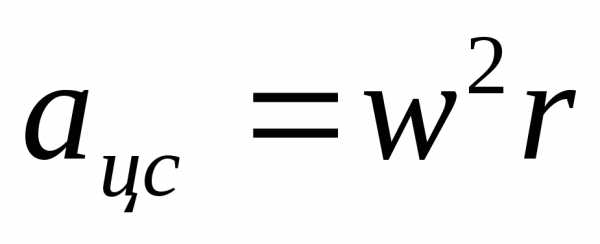

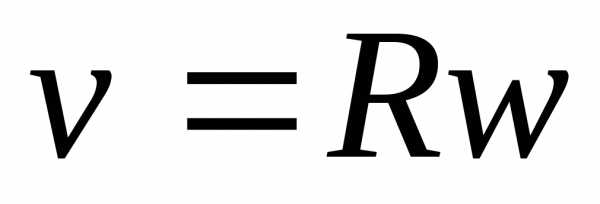

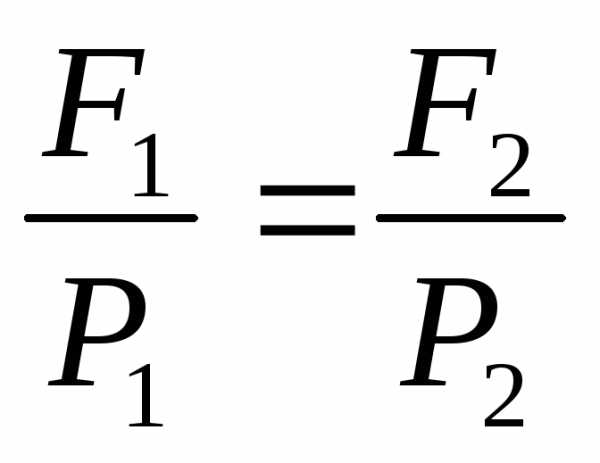
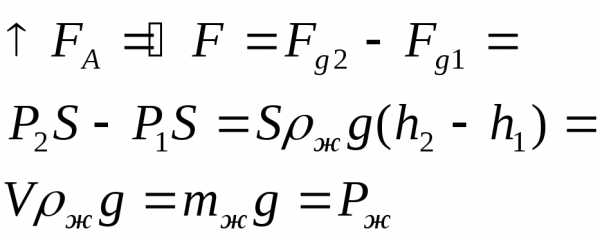
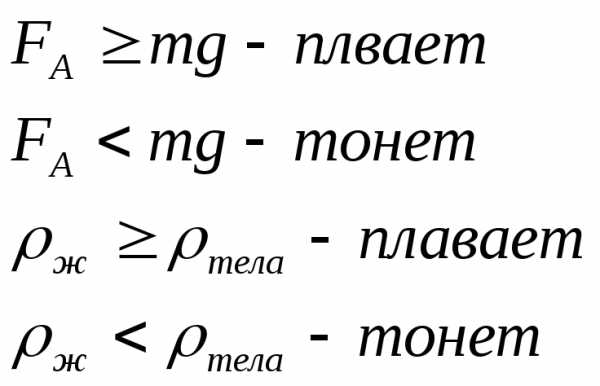


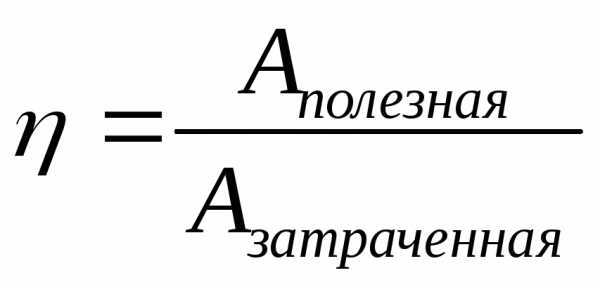

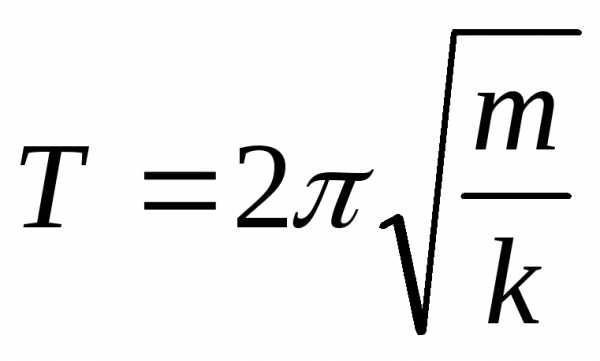
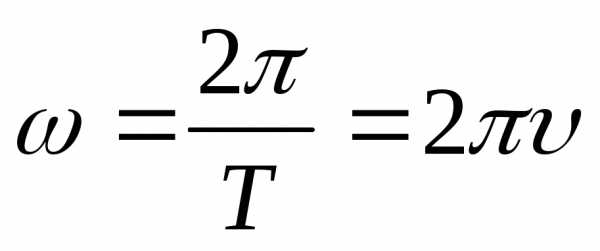
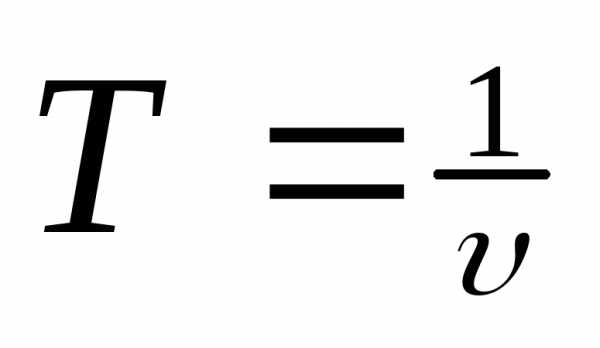

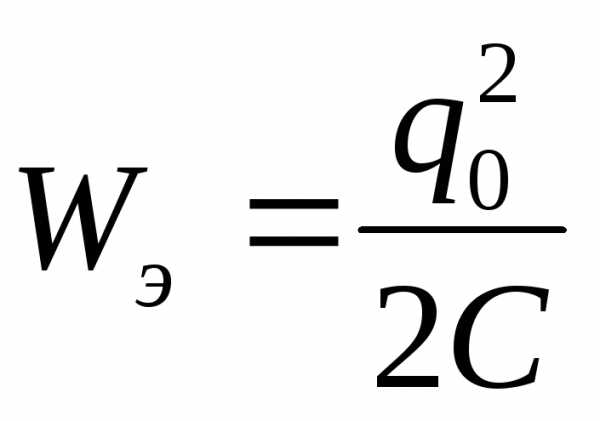

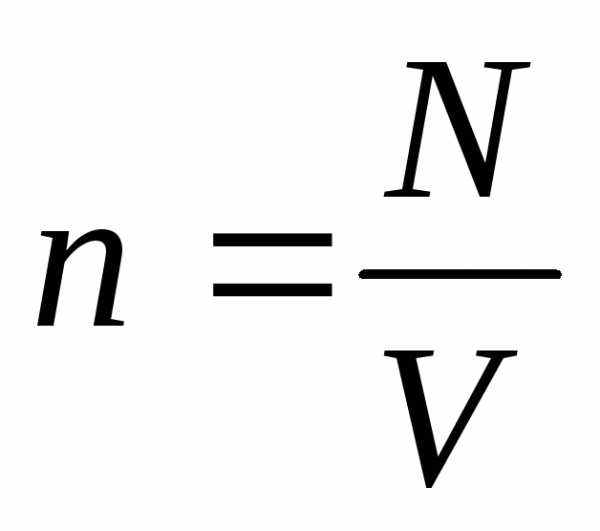
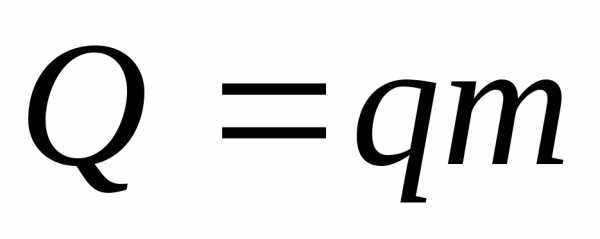

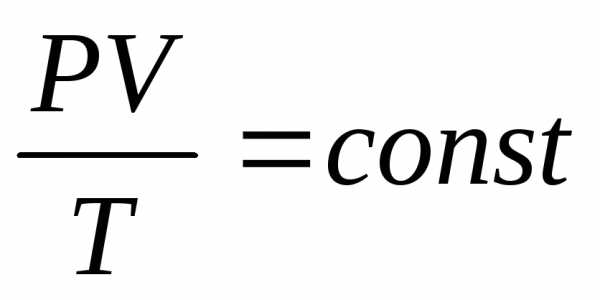
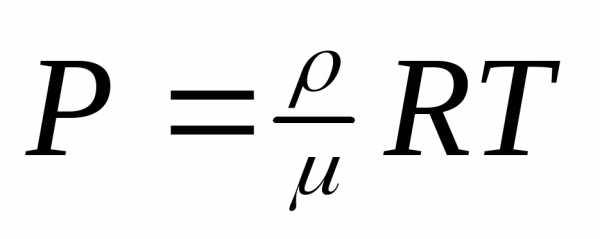





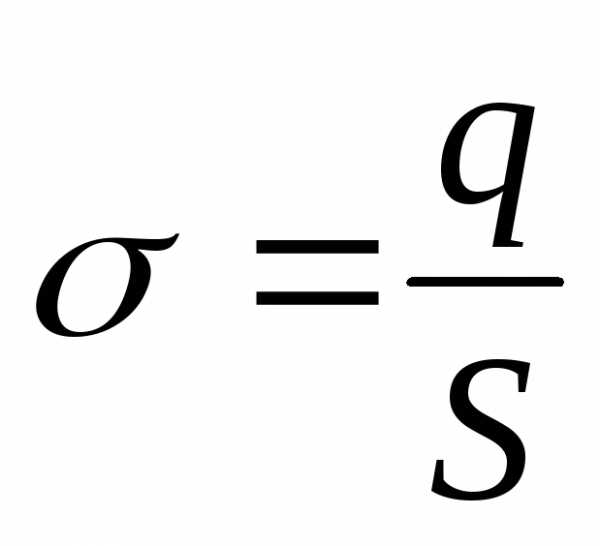

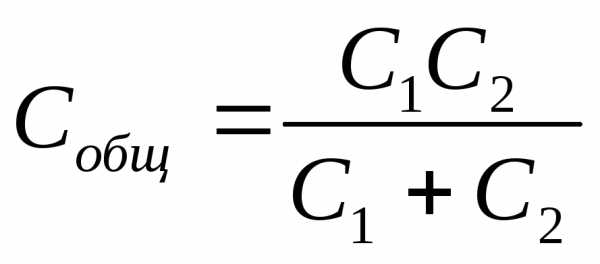
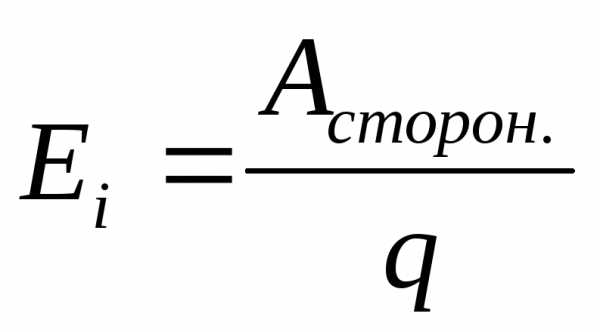
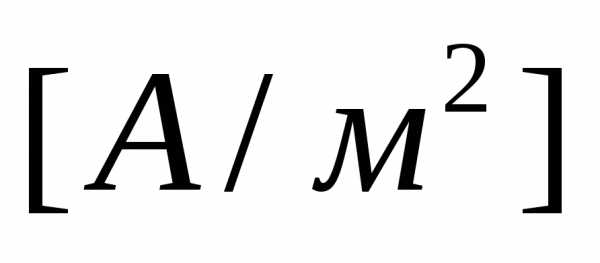

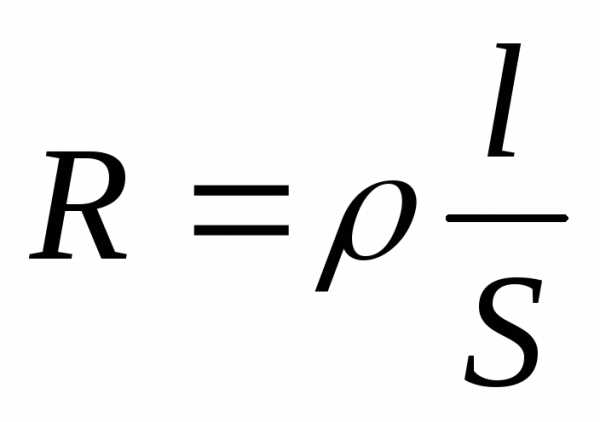

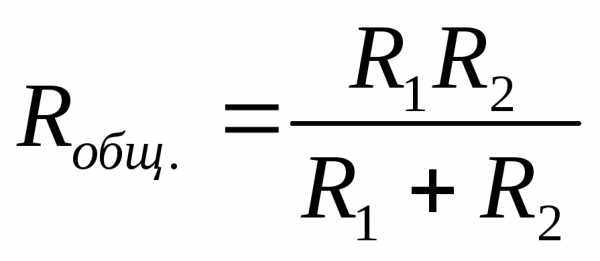
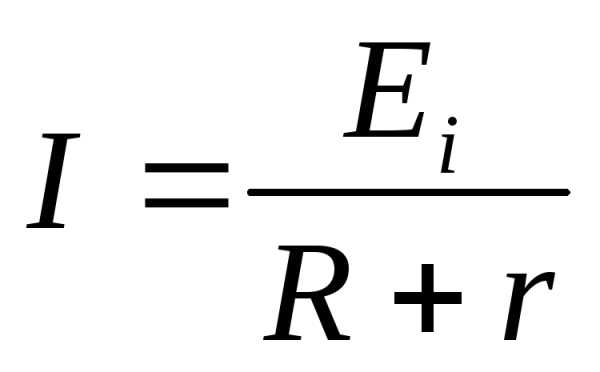
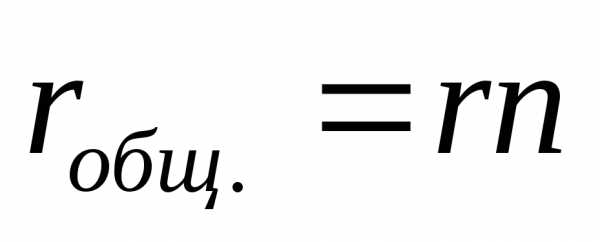

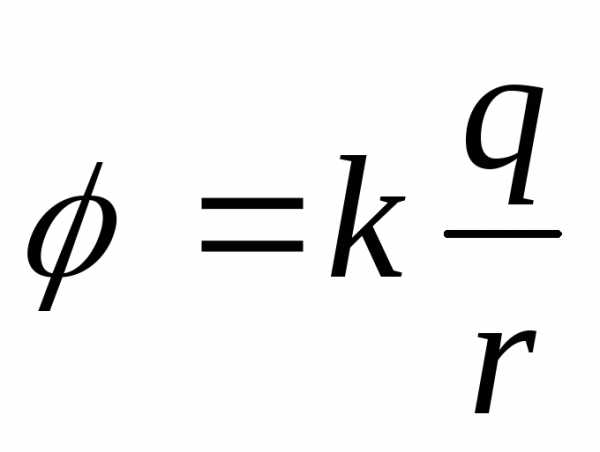
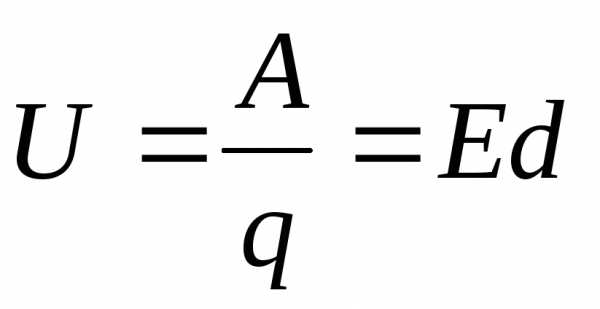
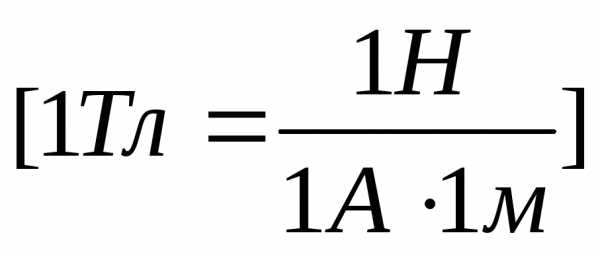


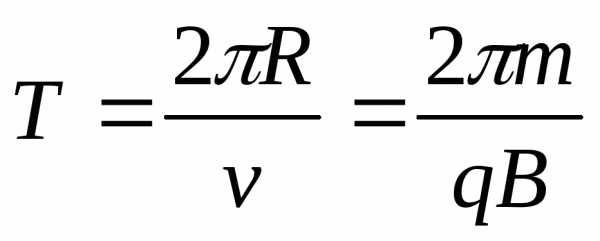
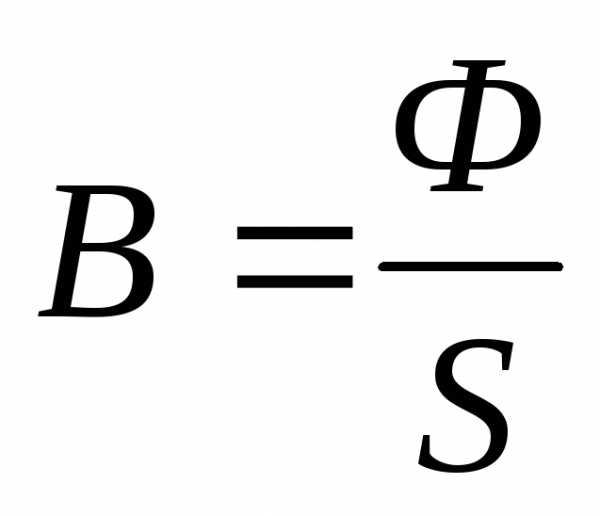
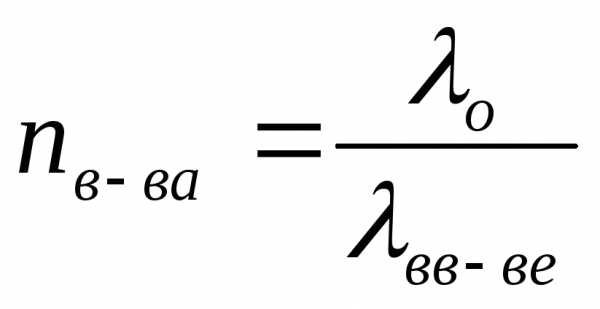
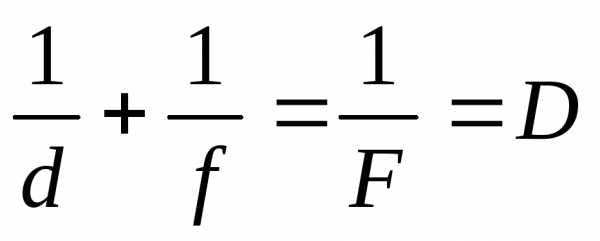
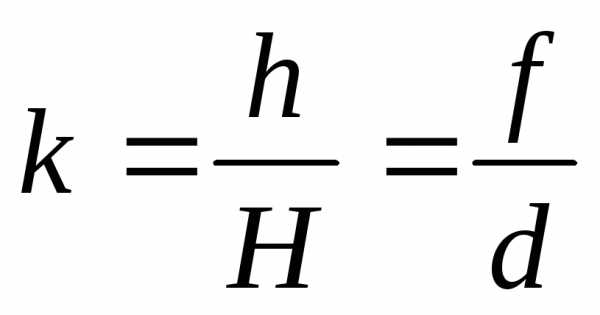
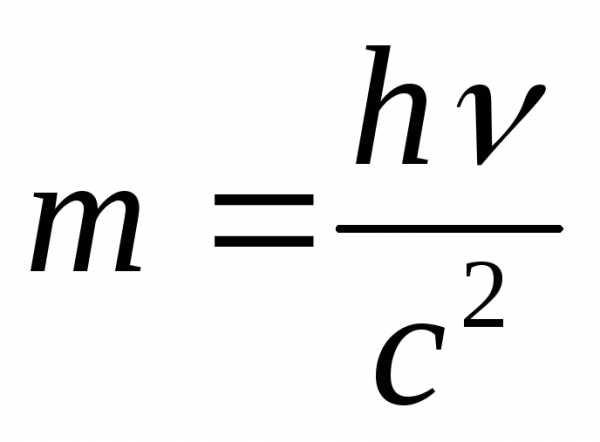
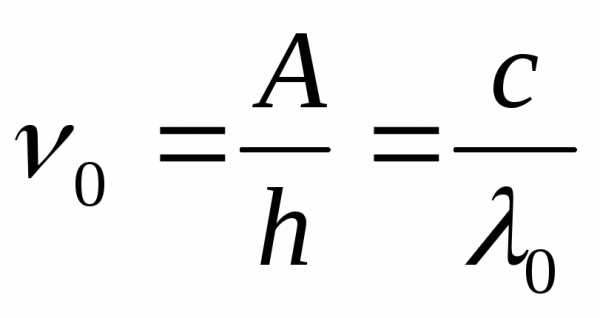
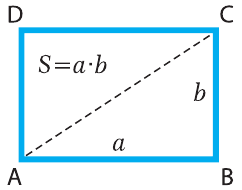
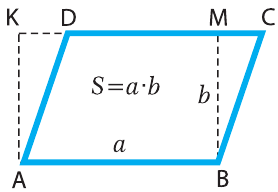
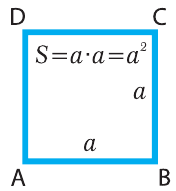
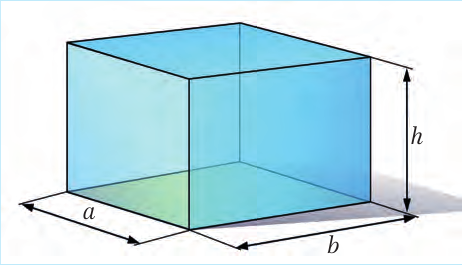
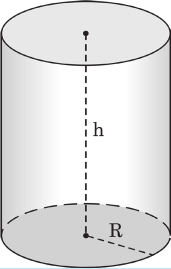
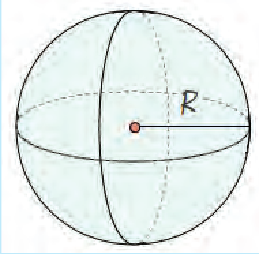 Рис. 6.6.
Рис. 6.6.