lxtik
#5021
2011-03-08 04:13 GMT
Пользователи
6 сообщений
Репутация 0 [-][+]
[img][/img]
Как решить не получается?
Знаю что P=F
p=g*p*h
p= P/S
как вычислить?
Личное сообщение
iskander
#5023
2011-03-08 19:40 GMT
Администраторы
3361 сообщений
http://alexandr4784.narod.ru/
Откуда: Псков
Кто: книгоиздательство
Репутация 179 [-][+]
Гиря давит на камеру силой
(F=mg)
и создает в камере давление
(p=frac{F}{S})
такое же давление и в трубке
(p=rho{gh})
Приравниваем давления и находим площадь.
Личное сообщение
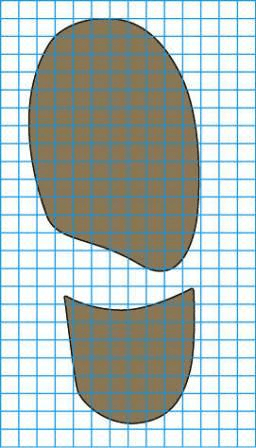
Зная свою массу и площадь ботинка, вычислите, какое давление вы производите при ходьбе и какое — стоя на месте.
Указание. Площадь опоры ботинка определите следующим образом. Поставьте ногу на лист клетчатой бумаги и обведите контур той части подошвы, на которую опирается нога (рис. 94).
рис. 94.
Сосчитайте число полных квадратиков, попавших внутрь контура, и прибавьте к нему половину числа неполных квадратиков, через которые прошла линия контура. Полученное число умножьте на площадь одного квадратика (площадь квадратика на листе, взятом из школьной тетради, равна
1
4
с
м
2
) и найдите площадь подошвы.
reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. §36. Задание. Номер №1
Решение
Определим площадь подошвы:
S = 465 + (1/2 *80) * 1/4 = 126,25
с
м
2
Стоя, человек оказывает давление на пол двумя на ногами.
p
=
F
2
S
;
F=gm;
p
=
g
m
2
S
;
g ≈10 Н/кг;
m = 50 кг;
p
=
10
∗
50
2
∗
126
,
25
≈ 1,9802 Н/
с
м
2
=
1
,
9802
0
,
0001
Н/
м
2
= 19802 Па = 19,8 кПа
Идя по земле, давление оказывается в среднем одной ногой, поэтому
p
=
F
S
;
p
=
10
∗
50
126
,
25
≈ 3,9604 Н/
с
м
2
=
3
,
9604
0
,
0001
Н/
м
2
= 39604 Па = 39,6 кПа
Ответ. 19,8 кПа; 39,6 кПа.
Сила трения скольжения — сила, возникающая между соприкасающимися телами при их относительном движении и направленная против движения
Ft = μ·N
Сила нормальной реакции опоры N=m·g, поэтому Ft = μ·m·g
Вектор силы трения скольжения всегда направлен противоположно вектору скорости движения тела относительно соприкасающегося с ним тела. Поэтому действие силы трения скольжения всегда приводит к уменьшению модуля относительной скорости тел.
Сила трения скольжения зависит от силы давления тел друг на друга (силы нормальной реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения и не зависит от площади соприкосновения. Это можно объяснить тем, что увеличивая площадь соприкосновения, мы уменьшаем удельное давление тел друг на друга.
Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается чаще всего латинской буквой μ. Обычно коэффициент трения меньше единицы. Он зависит от материалов соприкасающихся тел и от качества обработки поверхностей. При скольжении сила трения направлена по касательной к соприкасающимся поверхностям в сторону, противоположную относительной скорости
Обозначения:
Ft — сила трения
μ – коэффициент трения
N – сила нормальной реакции опоры
m — масса тела
g — ускорение свободного падения
Сила трения
Сила трения – сила механического сопротивления, возникающая в плоскости соприкосновения двух прижатых друг к другу тел при их относительном перемещении.
Сила сопротивления, действующая на тело, направлена противоположено относительному перемещению данного тела.
Сила трения возникает по двум причинам: 1) первая и основная причина заключается в том, что в местах соприкосновения молекулы веществ притягиваются друг к другу, и для преодоления их притяжения требуется совершить работу. Соприкасающиеся поверхности касаются друг друга лишь в очень небольших по площади местах. Их суммарная площадь составляет 0,01÷0,0010,01 div 0,001 от общей (кажущейся) площади соприкосновения. При скольжении площадь реального соприкосновения не остается неизменной. Сила трения (скольжения) будет изменяться в процессе движения. Если тело, которое скользит, прижать сильнее к телу, по которому происходит скольжение, то вследствие деформации тел площадь пятен соприкосновения (и сила трения) увеличится пропорционально прижимающей силе.
$$F_text{тр} sim F_text{приж}$$
2) вторая причина возникнове ния силы трения – это наличие шероховатостей (неровностей) поверхностей, и деформация их при движении одного тела по поверхности другого. Глубина проникновения (зацепления) шероховатостей зависит от прижимающей силы, а от этого зависит и величина деформаций. Последние, в свою очередь, определяют величину силы трения: Fтр∼FприжF_mathrm{тр} sim F_mathrm{приж}.
При относительном скольжении обе причины имеют место, потому характер взаимодействия имеет вид простого соотношения:
Fтр=μN -boxed{F_mathrm{тр} =mu N} -сила трения скольжения (формула Кулона — Амонтона), где
μ -mu — коэффициент трения скольжения,
N -N — сила реакции опоры, равная прижимающей силе.
Величина коэффициента трения различна для разных комбинаций трущихся веществ даже при одинаковой их обработке (силы притяжения и упругие свойства зависят от рода вещества).
Если между трущимися поверхностями будет находится смазка, то сила притяжения изменится заметным образом (будут притягиваться другие молекулы, и сила трения скольжения частично заменится силой вязкого трения, которую мы рассмотрим ниже).
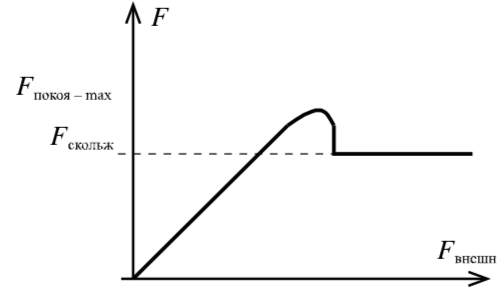
Если на тело, лежащее на горизонтальной поверхности, действует горизонтальная сила F→vec F, то движение будет вызвано этой силой только в том случае, когда она станет больше некоторого значения (μN)(mu N). До начала движения внешняя сила скомпенсирована силой трения покоя.
 |
| Рис. 13 |
Сила трения покоя всегда равна внешней силе, параллельной поверхности, и возникает по причине притяжения между молекулами в областях пятен соприкосновения и деформации шероховатостей.
Сила трения покоя различна в разных участках поверхности по которой будет происходить движение. Если тело долго лежит на поверхности, то вследствие вибраций (они всегда присутствуют на поверхности Земли) площадь пятен соприкосновения незначительно увеличится. Поэтому для начала движения придётся преодолеть немного большую силу трения, чем сила трения скольжения. Данное явление называется явлением застоя. С этим явлением мы сталкиваемся, например передвигая мебель в комнате. (На рисунке 13 превосходство трения покоя над трением скольжения сильно преувеличено).
Силой трения покоя мы пользуемся для перемещения на лыжах или просто при ходьбе.
Рассмотренные виды силы трения относятся к сухому трению или внешнему. Но есть еще один вид силы трения – вязкое трение.
При движении тела в жидкости или газе происходят достаточно сложные процессы обмена молекулами между слоями обтекающей жидкости или газа. Эти процессы называют процессами переноса.
При небольших скоростях движения тела относительно газа или жидкости сила сопротивления будет определяться выражением:
Fтр=6πηrv -boxed{F_mathrm{тр} = 6pi eta r v} — закон Стокса для шара, где
η -eta — вязкость вещества, в котором движется тело;
r -r — средний поперечный размер (радиус) тела;
v -v — относительная скорость тела;
6π -6pi — коэффициент, соответствующей сферической форме тела.
Вывод о величине скорости (большая она или маленькая) можно сделать, определив безразмерный коэффициент, называемый числом Рейнольдса:
Re=ρrvη -boxed{Re = frac{rho r v}{eta}} — число Рейнольдса, где
ρ -rho — плотность вещества, в которой движется тело.
Если Re<1700Re < 1700, то движение газа (жидкости) вокруг тела ламинарное (слоистое), и скорости можно считать малыми.
Если Re>1700Re > 1700, то движение газа (жидкости) вокруг тела турбулентное (с завихрениями), и скорости можно считать большими.
В последнем случае на образование вихрей тратится большая часть кинетической энергии тела, а значит, сила трения становится большей, а зависимость перестаёт быть линейной.
Fтр=kv2ρS -boxed{F_mathrm{тр} = kv^2rho S} — сила вязкого трения при больших скоростях, где
S -S — площадь поперечного сечения тела,
k -k — постоянная величина, зависящая от поперечных размеров тела.
Часто последнюю формулу можно видеть в виде:
[F_text{тр} = beta v^2.]
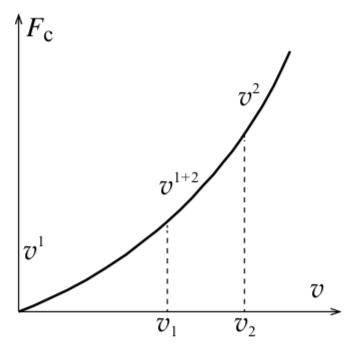
Число Рейнольдса, выбранное равным 17001700, в действительности определяется конкретной задачей (условиями) и может принимать другие значения того же порядка. Объясняется это тем, что зависимость силы вязкого трения от скорости носит сложный характер: при некотором значении скорости линейная зависимость начинает нарушаться, а при некотором значении скорости эта зависимость становится квадратичной.
 |
| Рис. 14 |
В промежутке от v1v_1 до v2v_2 степень принимает дробные значения (рис. 14) . Число Рейнольдса характеризует состояние динамической системы, при котором движение слоёв остаётся ламинарным, и сильно зависит от внешних условий. К примеру: стальной шар, двигаясь в воде вдали от границ жидкости (в океане, озере) сохраняет ламинарным движение слоёв при Re=1700Re = 1700, а тот же шар, движущийся в вертикальной трубе немного большего, чем шар, радиуса, заполненной водой, уже при Re=2Re=2 вызовет появление завихрений воды вокруг шара. (Отметим, что число Рейнольдса не единственное, применяемое для описания подобного движения. Например, применяют ещё числа Фруда и Маха.)
Из-за такой сложной зависимости силы сопротивления от размеров, формы тела и его скорости рассчитать с необходимой точностью силу сопротивления невозможно. Потому приходится создавать макеты летательных аппаратов и измерять силу сопротивления опытным путём, продувая воздух в аэродинамических трубах.
Пример 7. Сила сопротивления воздуха, действующая на капли тумана, пропорциональна произведению скорости на радиус капель: F=krvF = krv. Капли радиуса 0,1 мм0,1 text{мм}, падая с большой высоты, у земли имеют скорость около 1 м/с1 mathrm{м}/mathrm{с}. Какую скорость будут иметь капли, радиус которых в два раза меньше? В десять раз меньше?
Решение: Капля падает с постоянной скоростью, т. к. сила тяжести скомпенсирована силой вязкого трения о воздух: krv=mgkrv = mg или krv=ρ43πr3gkrv = rho frac 43 pi r^3 g, откуда v=4ρπg3kr2v = frac{4rhopi g}{3k}r^2.
Из полученного результата следует, что скорость капли прямо пропорциональна квадрату радиуса. Если радиус капли уменьшится в два раза, то скорость её падения уменьшится в четыре раза, и составит v1≈0,25 м/сv_1 approx 0,25 text{м}/text{с}; а если радиус окажется в десять раз меньше, то скорость будет в сто раз меньше, т. е. v2≈0,01 м/сv_2 approx 0,01 mathrm{м}/mathrm{с}.
Задача любопытна тем, что может объяснить почему облака не падают. Ведь облака – это туман, который не падает из-за наличия восходящих потоков воздуха. На нижней границе облака находятся наиболее крупные капли. Поднимаясь, скорость потока уменьшается, т. к. он совершает работу над встретившимся воздухом и увеличивает свою потенциальную энергию. Раз скорость потока в верхней части облака меньше, то и размер капель там тоже меньше. Капли «висят» над поверхностью земли на постоянной высоте.
Для того, чтобы решать задачи на тему «сообщающиеся сосуды», необходимо помнить следующее:
Закон сообщающихся сосудов: в неподвижных и открытых сообщающихся сосудах любой формы давление жидкости на любом горизонтальном уровне одинаково.
Следствие 1: в неподвижных и открытых сообщающихся сосудах высоты столбов жидкостей, отсчитываемые от уровня , ниже которого жидкость однородна, обратно пропорциональны плотностям этих жидкостей.
Следствие 2: в неподвижных и открытых сообщающихся сосудах однородная жидкость всегда устанавливается на одинаковом уровне независимо от формы сосудов.
Задача 1. Высота воды в левом колене сообщающихся сосудов см, в правом —
см. В каком направлении будет переливаться вода, если открыть кран? На сколько изменится уровень воды в левом сосуде? Найти объем воды, который перелился из одного сосуда в другой. Левое колено сосуда имеет площадь поперечного сечения
см
, правое
см
.
Показать
Задача 2. В сосуд с водой вставлена трубка сечением см
. В трубку налили машинное масло массой
г. Найти разность уровней масла и воды.
Трубка с маслом
Показать
Задача 3. В сообщающихся сосудах находятся ртуть и вода. Высота столба воды 68 см. Какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась в обоих сосудах на одном уровне?
Давление столба воды равно давлению столба керосина
Показать
Задача 4. В сообщающиеся сосуды налиты ртуть, вода и керосин. Какова высота слоя керосина, если высота столба воды 20 см и в правом колене уровень ртути ниже, чем в левом, на см?
Показать
Задача 5. Ртуть находится в сообщающихся сосудах. Площадь сечения левого колена в три раза меньше, чем правого. Уровень ртути в узком колене расположен на расстоянии 30 см от верхнего конца трубки. На сколько поднимется уровень ртути в правом колене, если левый медленно доверху залить водой?
Сообщающиеся сосуды разных объемов
Показать
Задача 6. Две трубки диаметром по см каждая представляют собой сообщающиеся сосуды. В одно колено сосуда заливают воду объемом
л, в другое —
л ртути. Каковы будут высоты жидкостей в обоих коленах? Объемом изогнутой части трубки пренебречь.
Показать
Задача 7. Барометрическая трубка сечением см
опущена в чашку с ртутью. На сколько изменится уровень ртути в чашке, если, не вынимая конца трубки из ртути, наклонить ее под углом
к вертикали? Диаметр чашки
см, атмосферное давление нормальное.
Наклонная трубка в чаше со ртутью
Показать
Задача 8. В вертикально расположенном сосуде переменного сечения находится вода, отделенная от атмосферы двумя невесомыми поршнями сечением и
. Поршни соединены тонкой проволокой длиной
. Найти силу натяжения проволоки, если трения нет.
Поршни, связанные нитью
Показать