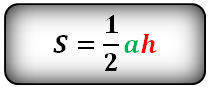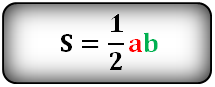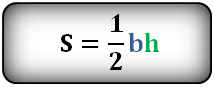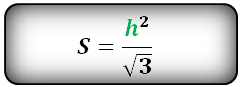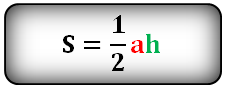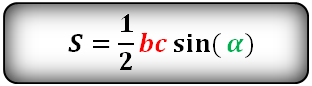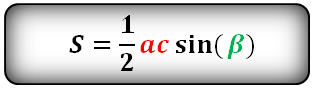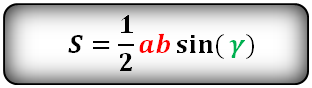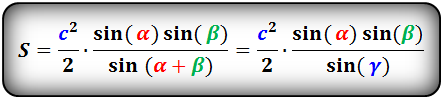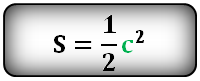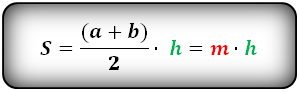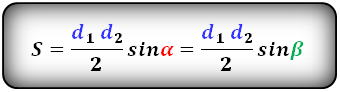Download Article
Download Article
There are many different shapes and many reasons why you might want to know their area! Whether you’re doing your homework or trying to figure out how much paint you’ll need to refurbish that living room, wikiHow has your back! Just get started with Step 1 below to learn how to calculate the area of a shape.
-
1
Measure the width and height. You’ll need to start by finding the width and height of the shape (in other words, by finding the measure of two adjoining sides).[1]
- For a parallelogram, you’ll need to use what are called the base and vertical height, but these are the same idea as width and height.
- In the real world, you’ll have to measure for yourself but for your homework your teacher should have these measurements listed with the shape.
-
2
Multiply the sides. Multiply the sides by each other.[2]
For example, if you have a rectangle with a height of 16 in and a width of 42 in, you’ll need to multiply 16 x 42.[3]
- If you’re calculating the area of a square you can actually save yourself some time when using a calculator and just square the side. So, if the side is 4 ft, click 4 and then the square button on your calculator to get the answer. Squaring automatically multiples the number by itself.
Advertisement
-
3
Get your result. The resulting number from the multiplication is the area of your shape, which is written as «square units». So the area for our rectangle would be 672 square inches.
- This is also sometimes referred to as inches square or written with a small 2 above the text line instead of the word «square».
Advertisement
-
1
Take your measurements. You’ll need the measurement of the base, the top, and the vertical height. The base and top are the two parallel sides, while the height will be taken on one of the sides with the angle.[4]
- In the real world, you’ll have to measure for yourself but for your homework your teacher should have these measurements listed with the shape.
-
2
Add the top and base measurements.[5]
Let’s say ours has a top that’s 5cm and a base that’s 7cm. That gives us a value of 12. -
3
Multiply that value by 1/2.[6]
That gives us a value of 6. -
4
Multiply that value by the height. For our trapezoid, let’s say that that’s 6cm. That gives us a value of 36.[7]
-
5
Get your result. The resulting number after you multiply the height is the area of the trapezoid. So for our 5x6x7 trapezoid, the area is 36 square cm.
Advertisement
-
1
Find the radius. In order to find the area of a circle, you’ll need to know the radius. This is the measurement of the distance between the center of the circle and the outside edge. You can also find this by taking the diameter, or the measurement of the width of the circle, and dividing it in half.[8]
- In the real world, you’ll have to measure for yourself but for your homework your teacher should have these measurements listed with the shape.
-
2
Square the radius. Multiply the radius times itself. Let’s say we have a radius that is 8 feet. That gives us a value of 64.
-
3
Multiply by pi. Pi (π) is a really big number that is used in lots of calculations. If you’re using a calculator, use the pi function for a really accurate result. If not, you can round pi (ignore some of the numbers) and just multiply by 3.14159. This gives us a value of 201.06176.[9]
-
4
Get your result. The resulting number, 201.06176 in our case, is the area of the circle. So we get a result of 201.06176 square feet.
Advertisement
-
1
Take your measurements. Sectors are portions of a circle, that come out looking a bit like fans. You’ll need to know the radius of the original circle, or one side of your «fan», as well as the angle of the point. For us, let’s say we have a radius of 14 inches and an angle of 60.[10]
- In the real world, you’ll have to measure for yourself but for your homework your teacher should have these measurements listed with the shape.
-
2
Square the radius. Multiply the radius times itself. This gives us a value of 196 (14×14).
-
3
Multiply by pi. Pi (π) is a really big number that is used in lots of calculations. If you’re using a calculator, use the pi function for a really accurate result. If not, you can round pi (ignore some of the numbers) and just multiply by 3.14159. That gives us a value of 615.75164.[11]
-
4
Divide the angle by 360. Now, you’ll need to take the angle of the point and divide that number by 360 (which is the number of degrees in a circle). For us, we get a value of roughly .166. It’s technically a repeating number, but we’re going to round to make the math easier.[12]
-
5
Multiply the resulting number by the number you got earlier. Multiply the number you get when you divide by 360 by the number you got earlier after you multiply by pi.[13]
For us, this gives a result of about 102.214. -
6
Get your result. This resulting number is the area of your sector, making our sector 102.214 square inches.
Advertisement
-
1
Get your measurements. To get the area of an ellipse, you’ll need to know the two «radio», which you can think of as the width and the height each divided in half. These are the measurements from the center to the middle of the long side and from the center to the middle of the short side. The measurement lines should form a right angle.
- In the real world, you’ll have to measure for yourself but for your homework your teacher should have these measurements listed with the shape.
-
2
Multiply the two radii.[14]
For us, let’s say that the ellipse is 6 inches wide and 4 inches tall. This gives us radii of 3 inches and 2 inches. Now, we’ll multiply those numbers by each other, giving us 6 (3×2).[15]
-
3
Multiply that number by pi.[16]
Pi (π) is a really big number that is used in lots of calculations. If you’re using a calculator, use the pi function for a really accurate result.[17]
If not, you can round pi (ignore some of the numbers) and just multiply by 3.14159. That gives us a value of 18.84954. -
4
Get your result. That resulting number is the area of your ellipse. For us, that means our ellipse is 18.84954 square inches.
Advertisement
-
1
Find your measurements. You’ll need to know the base measurement of the triangle as well as the height. The base can be any side of the triangle, as long as you can also measure the height. Let’s say that we have a triangle with a base of 3 meters and a height of 1 meter.[18]
- In the real world you’ll have to measure for yourself but for your homework your teacher should have these measurements listed with the shape.
-
2
Multiply the base by the height. For us, this gives a value of 3 (3×1).[19]
-
3
Multiply that value by 1/2.[20]
This gives us a value of 1.5. -
4
Get your result. That resulting value is the area of the triangle. So we get a result of 1.5 square meters.
Advertisement
-
1
Break the shape down into sections. You’ll have to start finding the area for complex shapes by breaking the shape down into geometric shapes, like those discussed above. On homework assignments, it will probably be pretty clear cut what those shapes should be, but in the real world, you might need to break an area up into a lot of shapes in order to get really accurate.[21]
- A good place to start is by looking for right angles and parallel lines. These serve as the basis of many shapes.
-
2
Calculate the area of the separate shapes. Use the instructions above to find the area of the different shapes you find.[22]
-
3
Add the shapes together. Add the resulting areas together in order to get the total area for your shape.[23]
-
4
Use alternative methods. There are other tricks you can try too, depending on the shape. You can also try adding imaginary space in order to make the shape a standard geometric shape, and then subtracting the area of that imaginary space after you get your result, for example.
Advertisement
Add New Question
-
Question
How can I find the square inches of a triangle with a base of 15 inches and the height of 8 inches?
A triangle’s area is equal to one-half its base multiplied by its height. A = (15)(8) ÷ 2 = 60 sq in.
-
Question
A hexagonal prism is 13 cm long and has a volume of 370.5 cm squared. What would be area of the front side?
Divide the volume by the length to get the cross-sectional area. Assuming this is a regular hexagon, use the area formula to solve for the width of a side: A = (0.385)(s²). Multiply the side width thus calculated by the length of the prism. That gives you the area of one side.
-
Question
How can I calculate the area of a parallelogram with a base of 12cm, height of 5 cm, and the inside is 4 cm?
The area of a parallelogram is the base multiplied by the height.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Get help from a friend if you’re having a hard time!
Advertisement
-
Make sure that you keep your units of measurement straight. You don’t want to mix up numbers!
-
It’s a good idea to double check your answer!
Advertisement
References
About This Article
Article SummaryX
To find the area of a square or rectangle, just multiply the width of the shape by its height. To find the area of a circle, start by measuring the distance between the middle of the circle to the edge, which will give you the radius. Then, square the radius and multiply it by pi to find the area. If you need to find the area of a triangle, multiply the base of the triangle by its height. To find the area of a trapezoid, add the top and bottom of the shape together, divide that number in half, and then multiply by the height. To learn how to find the area of other shapes, such as ellipses or shapes that don’t fit one particular category, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 482,928 times.
Reader Success Stories
-
«Having a diagram with step-by-step calculations to follow was really useful!»
Did this article help you?
Почему бы просто не считать клеточки?
Возможно, вы читаете всё это и думаете: зачем все эти сложности? Формулы запоминать. Дорисовывать. Тут ведь сразу видно, сколько клеточек в фигуре.
Вот, например, трапеция:
Посчитаем клеточки: их всего 46, верно?
Но стоп, там же некоторые из них только наполовину внутри фигуры. Отметим их – всего таких 10. Итого, 36 полных (красные точки) и 10 половинчатых, вместе ( 36+frac{10}{2} = 41)
Вроде бы всё верно. Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…
Как всё это учитывать?
Попробуем рассуждать так: заметно, что тот маленький розовый треугольник дополняет серый кусок клетки.
А жёлтые сколько занимают? Постарайтесь ответить сами.
Если всё сделать правильно, то увидите, что жёлтые кусочки можно сложить вместе в одну целую клетку.
Итак, 2 жёлтых куска = 1 клетка.
Розовый треугольник + серый кусок = 1 клетка. Всего у нас две таких пары (розовый+серый) – это 2 полных клетки.
Всё остальное как было: 36 полных клеток и 6 половинок у правой стороны – это ( 36+frac{6}{2}=39) клетки.
Итого клеток: ( 1 + 2 + 39 = 42).
Проверим результат по формуле площади трапеции: нижнее основание 11, верхнее основание 3, высота 6. Полусумма оснований равна 7, умножаем на высоту – получилось 42. Всё совпало.
Но! Настолько ли проще был наш способ подсчёта клеточек? Не сказал бы. А если там будет несколько косых линий, то вообще можно замучиться собирать этот паззл (искать, какие кусочки друг друга дополняют).
Вычислите площадь простых фигур тремя способами
Стороны клеток равны 1. Вычислите самостоятельно площадь фигуры всеми тремя способами. Сравните результаты.
Вычислите площадь произвольных фигур по формуле Пика
Вычислите самостоятельно площади фигур с помощью формулы Пика:
Посчитайте площадь корабля и котика по формуле Пика
Посчитайте самостоятельно для тренировки и чтобы запомнить формулу Пика!
Фигуры с отверстиями — посчитайте площади двумя способами
Ну и напоследок фигуры с «дырками». Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?
Или достаточно просто посчитать точки внутри закрашенной области и на её границах (в том числе, на границе с дыркой)?
Проверим на простом примере: это квадрат ( 4times 4), и в нём вырезан прямоугольник ( 1times 2), значит, его площадь ( 16-2=14).
А теперь по точкам. На границах (включая внутренние) ( Г = 22). Внутри ( В = 3). Тогда площадь по формуле Пика
( S = frac{22}{2} + 3 -1 = 13.)
Хм, близко, но не совпало. Может, я где-то ошибся? Давай ещё одну фигуру, для верности.
Сосчитай сам и проверь.
Что получилось?
У меня снова на 1 меньше.
Так может быть просто формулу немного «подкрутить»? Нет!
Очень и очень не рекомендую вам запоминать несколько похожих формул для похожих случаев, потому что придёт время, и вы обязательно перепутаете формулу.
Даже если вы уверены, что не перепутаете, оно всё равно того не стоит. В общем, наилучший вариант – это запомнить одну формулу. А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.
Площадь поверхности пирамиды
Для пирамиды тоже действует общее правило:
Площадь полной поверхности пирамиды – это сумма площадей всех граней.( displaystyle {{S}_{полн. пов. }}={{S}_{боков.пов. }}+{{S}_{основания }})
Теперь давай посчитаем площадь поверхности самых популярных пирамид.
Площадь поверхности правильной треугольной пирамиды
Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle {{S}_{ASB}}).
И тогда
( displaystyle {{S}_{полн. пов. }}=3{{text{S}}_{ASB}}+{{text{S}}_{text{осн}.}})
Вспомним теперь, что
( displaystyle {{S}_{осн}}) — это площадь правильного треугольника ( displaystyle ABC).
И еще вспомним, как искать эту площадь.
Используем формулу площади:
( displaystyle S=frac{1}{2}abcdot sin gamma ).
У нас «( displaystyle a)» — это ( displaystyle a), а «( displaystyle b)» — это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2}).
Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).
Теперь найдем ( displaystyle {{S}_{Delta ASB}}).
Пользуясь основной формулой площади и теоремой Пифагора, находим
( displaystyle {{S}_{Delta ASB}} = frac{1}{2}asqrt{b^2-frac{a^2}{4}})
Внимание: если у тебя правильный тетраэдр (т.е. ( displaystyle b=a)), то формула получается такой:
( displaystyle S={{a}^{2}}sqrt{3}).
Загрузить PDF
Загрузить PDF
Иногда вычисление площади сводится к простому перемножению двух чисел, но зачастую это вычисление более сложное. Прочтите эту статью для краткого обзора по вычислению площади (или площади поверхности) следующих фигур: четырехугольник, квадрат, параллелограмм, трапеция, треугольник, многоугольник, круг, пирамида, цилиндр, кривая линия.
-
1
Найдите длину двух смежных сторон прямоугольника. Поскольку противоположные стороны прямоугольника равны, нужно найти длины смежных сторон. Обозначьте одну сторону как (b), а другую — как (h).[1]
-
2
Перемножьте значения двух смежных сторон, чтобы найти площадь. Обозначим площадь прямоугольника как (k). Тогда: k = b*h.
- Для более детальных инструкций прочтите статью «Как найти площадь четырехугольника».
Реклама
-
1
Найдите длину стороны квадрата. Поскольку квадраты имеют четыре равные стороны, нужно найти длину всего одной стороны.[2]
-
2
Возведите в квадрат длину стороны. Это и есть площадь квадрата.
- Это верно, потому что квадрат — это прямоугольник, у которого все стороны равны. Так как для прямоугольника k = b*h, а в квадрате b=h, для вычисления площади квадрата просто умножаем его сторону на саму себя.
Реклама
-
1
Выберите одну сторону, на которую будет опущен перпендикуляр. Найдите длину этой стороны.
-
2
Опустите перпендикуляр (высоту) на выбранную ранее сторону и найдите его длину.[3]
- Если нужно, продлите сторону, на которую опускается перпендикуляр, до ее пересечения с перпендикуляром.
-
3
Реклама
-
1
Найдите длины двух параллельных сторон. Обозначьте их как (а) и (b).
-
2
Найдите высоту. Опустите перпендикуляр (высоту (h)) к основанию трапеции.[5]
-
3
Реклама
-
1
Найдите длину одной стороны треугольника (b), на которую будет опущен перпендикуляр (высота) и длину высоты (h).
-
2
Чтобы найти площадь треугольника, подставьте длину соответствующей стороны и длину высоты в формулу: A=0.5b*h
- Для более детальных инструкций прочтите статью «Как найти площадь треугольника».
Реклама
-
1
Найдите длину стороны и длину апофемы (а) (отрезок, соединяющий центр многоугольника и середину любой из его сторон).
-
2
Умножьте длину стороны на количество сторон, чтобы найти периметр многоугольника (р).
-
3
Реклама
-
1
Найдите радиус окружности (r). Это отрезок, соединяющий центр окружности и любую точку на окружности.
-
2
Реклама
-
1
Найдите площадь прямоугольного основания пирамиды с помощью приведенной выше формулы для нахождения площади прямоугольника: k=b*h.
-
2
Найдите площадь каждой треугольной грани пирамиды с помощью приведенной выше формулы для нахождения площади треугольника: A=0.5b*h.
-
3
Сложите все полученные площади для вычисления площади поверхности пирамиды.
Реклама
-
1
Найдите радиус круга в основании цилиндра.
-
2
Найдите высоту цилиндра.
-
3
Найдите площадь круга в основании, используя формулу для вычисления площади круга: А=πr^2.
-
4
Найдите площадь боковой поверхности, умножив высоту цилиндра на периметр основания. Периметр основания равен длине окружности: P = 2πr, поэтому площадь боковой поверхности А= 2πhr.
-
5
Сложите все полученные площади: две площади круговых оснований и площадь боковой поверхности. Таким образом, площадь поверхности цилиндра: SA = 2πr^2 + 2πhr.
- Для более детальных инструкций прочтите статью «Как найти площадь поверхности цилиндра».
Реклама
Допустим, вы хотите найти площадь фигуры, ограниченной кривой линией (описывается функцией f(x)), осью x и значениями функции при x=а и при x=b (то есть область определения [a,b]). Этот метод потребует знаний интегрального исчисления. Если вы не знаете его, этот метод не имеет для вас никакого смысла.
-
1
Определите f(x) через x.
-
2
Возьмите интеграл функции f(x) в интервале [а,b]. По формуле Ньютона-Лейбница: F(x)=∫f(x), ∫abf(x) = F(b) — F(a).
-
3
Подставьте значения а и b в интегральное выражение. Искомая площадь определяется как ∫abf(x). Поэтому, A=F(b)) — F(a).
Реклама
Об этой статье
Эту страницу просматривали 25 331 раз.
Была ли эта статья полезной?
Как найти площадь любого треугольника
Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.
Как найти площадь любого треугольника
Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.
Зная сторону и высоту
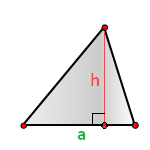
- Умножьте сторону треугольника на высоту, проведённую к этой стороне.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — сторона треугольника.
- h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.
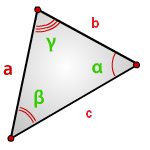
Зная две стороны и угол между ними
- Посчитайте произведение двух известных сторон треугольника.
- Найдите синус угла между выбранными сторонами.
- Перемножьте полученные числа.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a и b — стороны треугольника.
- α — угол между сторонами a и b.
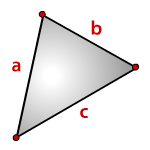
Зная три стороны (формула Герона)
- Посчитайте разности полупериметра треугольника и каждой из его сторон.
- Найдите произведение полученных чисел.
- Умножьте результат на полупериметр.
- Найдите корень из полученного числа.
- S — искомая площадь треугольника.
- a, b, c — стороны треугольника.
- p — полупериметр (равен половине от суммы всех сторон треугольника).
Зная три стороны и радиус описанной окружности
- Найдите произведение всех сторон треугольника.
- Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.
- S — искомая площадь треугольника.
- R — радиус описанной окружности.
- a, b, c — стороны треугольника.
Зная радиус вписанной окружности и полупериметр
Умножьте радиус окружности, вписанной в треугольник, на полупериметр.
- S — искомая площадь треугольника.
- r — радиус вписанной окружности.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
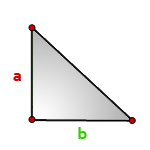
Как найти площадь прямоугольного треугольника
- Посчитайте произведение катетов треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.
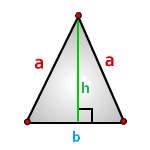
Как найти площадь равнобедренного треугольника
- Умножьте основание на высоту треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
- h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.
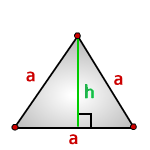
Как найти площадь равностороннего треугольника
- Умножьте квадрат стороны треугольника на корень из трёх.
- Поделите результат на четыре.
- S — искомая площадь треугольника.
- a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.
Читайте также 🧠👨🏻🎓✍🏻
- 7 причин полюбить математику
- ТЕСТ: Помните ли вы геометрию?
- 10 хитрых головоломок со спичками для тренировки воображения
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- ТЕСТ: Сможете ли вы решить простые математические примеры?
Содержание
- Формулы площадей всех основных фигур
- 1. Формула площади круга через радиус или диаметр
- 2. Формула расчета площади треугольника
- 3. Площадь треугольника, формула Герона
- 4. Площадь прямоугольного треугольника по катетам
- 5. Как вычислить площадь равнобедренного треугольника ?
- 6. Площадь равностороннего треугольника равна:
- 7. Найти площадь треугольника, угол и две стороны
- 8. Площадь треугольника по стороне и двум углам, формула.
- 9. Формула расчета площади прямоугольника
- 10. Как рассчитать площадь квадрата через диагональ или сторону
- 11. Формулы площади параллелограмма
- 12. Площадь произвольной трапеции
- 13. Площадь равнобедренной трапеции
- Площадь фигур
- Вычислить, найти площадь геометрических фигур
Формулы площадей всех основных фигур
1. Формула площади круга через радиус или диаметр
Зная диаметр или радиус круга, можно найти его площадь.
r — радиус круга
D — диаметр
Формула площади круга, (S):
2. Формула расчета площади треугольника
h — высота треугольника
a — основание
Площадь треугольника (S):
3. Площадь треугольника, формула Герона
a , b , c , — стороны треугольника
p— полупериметр, p=( a + b + c )/2
Формула ( Герона ) площади треугольника через полупериметр ( S ):
4. Площадь прямоугольного треугольника по катетам
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.
a , b — катеты треугольника
Формула площади прямоугольного треугольника, (S):
5. Как вычислить площадь равнобедренного треугольника ?
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b , ( S ):
Формула площади треугольника через, стороны a , b , (S):
6. Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h — высота
Площадь треугольника только через сторону a , (S):
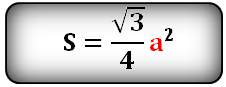
Площадь треугольника только через высоту h , ( S ):
Площадь треугольника через сторону a и высоту h , (S):
7. Найти площадь треугольника, угол и две стороны
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.
a , b , c — стороны треугольника
α , β , γ — углы
Формулы площади треугольника, через две стороны и угол между ними, ( S ):
8. Площадь треугольника по стороне и двум углам, формула.
a , b , c — стороны треугольника
α , β , γ — противолежащие углы
Площадь треугольника через сторону и два угла (S):
9. Формула расчета площади прямоугольника
b — длина прямоугольника
a — ширина
Формула площади прямоугольника, (S):
10. Как рассчитать площадь квадрата через диагональ или сторону
a — сторона квадрата
c — диагональ
Формула площади квадрата через сторону a , (S):
Формула площади квадрата через диагональ c , (S):
11. Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α , β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, ( S ):
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
H b — высота на сторону b
H a — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d — меньшая диагональ
α , β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
12. Площадь произвольной трапеции
1. Формула площади трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
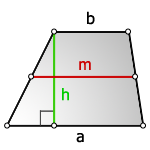
m — средняя линия
h — высота трапеции
Формула площади трапеции, (S):
2. Формула площади трапеции через диагонали и угол между ними
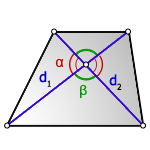
d 1, d 2 — диагонали трапеции
α , β — углы между диагоналями
Формула площади трапеции, (S):
3. Формула площади трапеции через четыре стороны
b — верхнее основание
a — нижнее основание
c, d — боковые стороны
Формула площади трапеции, (S):
13. Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α , β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α , β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α , β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Источник
Площадь фигур
Площадь фигуры является суммарной числовой характеристикой всех единичных квадратных элементов плоскости. В зависимости от размера фигур стороны квадрата единичного элемента могут быть равны 1 мм, см, м, дюйму, км и пр. S фигур могут измеряться в следующих единицах измерения: мм2, см2, м2, гектарах, квадратных километрах и пр.
Вычислить, найти площадь геометрических фигур
| Онлайн Расчеты и формулы площади для плоских фигур | |
| Площадь треугольника калькулятор нахождения площади треугольников |
Площадь прямоугольного треугольника онлайн формула площади прямоугольного треугольника |
| Площадь равнобедренного треугольника найти площади равнобедренных треугольников |
Площадь равностороннего треугольника вычислить площадь равностороннего треугольника |
| Площадь треугольника по формуле Герона площадь Герона, формула |
Площадь квадрата чему равна площадь квадрата |
| Площадь прямоугольника как найти чему равна площадь прямоугольника |
Площадь круга онлайн калькулятор площади круга через радиуса |
| Площадь ромба как найти площадь ромба через диагонали и т.д. |
Площадь параллелограмма онлайн калькулятор для нахождения площади параллелограмма |
| Площадь трапеции площадь прямоугольной и равнобедренной трапеции |
Площадь эллипса формула площади эллипса онлайн |
| Площадь кольца как вычислить площадь кольца онлайн |
Площадь четырехугольника чему равна площадь четырехугольника, формула |
| Площадь сектора кольца подсчитать площади сектора кольца |
Площадь сектора круга получить площадь сектора круга |
| Площадь сегмента круга решить площадь сегмента круга |
|
| Онлайн Расчеты и формулы площади для объемных фигур | |
| Площадь шара калькулятор нахождения площадь поверхности сферы или шара |
Площадь куба как найти чему равна площадь поверхности куба |
| Площадь цилиндра калькулятор для нахождения площади поверхности и основания цилиндра |
Площадь пирамиды формулы расчета площади боковой поверхности и основания пирамиды |
| Площадь параллелепипеда калькулятор площади параллелепипеда прямоугольного и др. |
Площадь конуса нахождение площади поверхностей конуса |
| Площадь усеченного конуса калькулятор нахождения площади поверхности усеченного конуса |
Площадь тетраэдра площадь поверхности и грани тетраэдра |
| Площадь призмы калькулятор нахождения площади поверхности и боковой площади призмы |
Площадь фигуры сложной формы может составляться из различных элементарных фигур: треугольников, квадратов, прямоугольников и пр. Общая площадь будет высчитываться путем суммирования площадей составляющих компонент.
Набор онлайн-калькуляторов страницы дает возможность оперативного вычисления не только S плоских фигур (квадрата, прямоугольника, круга, ромба, эллипса), но и площадей объемных фигур (куба, призмы, конуса, цилиндра, сферы, тетраэдра и пр.), являющихся совокупностью нескольких плоскостей.
Вычисление площадей фигур востребовано для решения различных задач:
— строительных;
— кадастровых;
— инженерных и пр.
Государство осуществляет кадастровый учет земельных участков, основным учитываемым параметром которых является площадь. Специалистами БТИ фиксируется общая и полезная жилая площадь квартир. В быту иногда нужно вычислять площадь ковра, натяжного потолка, площадь дачного участка и пр.
Источник