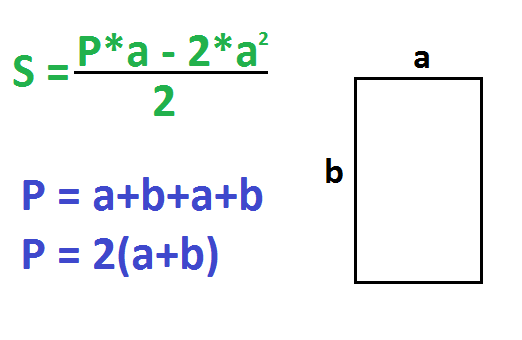Как найти площадь прямоугольника фотографии - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Прямоугольник — четырехсторонняя фигура с четырьмя прямыми углами, противолежащие стороны которой равны. Все, что нужно сделать для вычисления его площади, — умножить длину на ширину. Хотите знать как это сделать? Читайте дальше.

1
Прямоугольник — четырехсторонняя фигура, противолежащие стороны которой равны. Если одна сторона равна 10 см, то и противолежащая будет равна 10 см.
- Любой квадрат также является прямоугольником. Площадь квадрата находится по той же формуле.
2

Выучите формулу нахождения площади прямоугольника: S = a * b, где S — площадь, a — длина, b — ширина, то есть, площадь равна произведению сторон.

Реклама

1
Найдите длину прямоугольника. Как правило, она указана в задаче, но если нет — найдите ее с помощью линейки.
- Двойные отметки на длинных сторонах означают, что их длины равны.
2
Так же найдите ширину прямоугольника.
- Отметки на узких сторонах означают, что их ширины равны.
3

Запишите длину и ширину. В нашем примере длина — 5 см, ширина — 4 см.
4
Умножьте длину на ширину. Длина — 5 см, ширина — 4 см, вставьте эти числа в формулу S = a * b и вы найдете площадь.
- S = 4 cm * 5 cм
- S = 20 cм^2
5
Запишите ответ в квадратных единицах. Ответ: 20 см^2, что означает «двадцать квадратных сантиметров».
- Ответ можно записать как 20 кв. см, так и 20 см^2.
Реклама

1
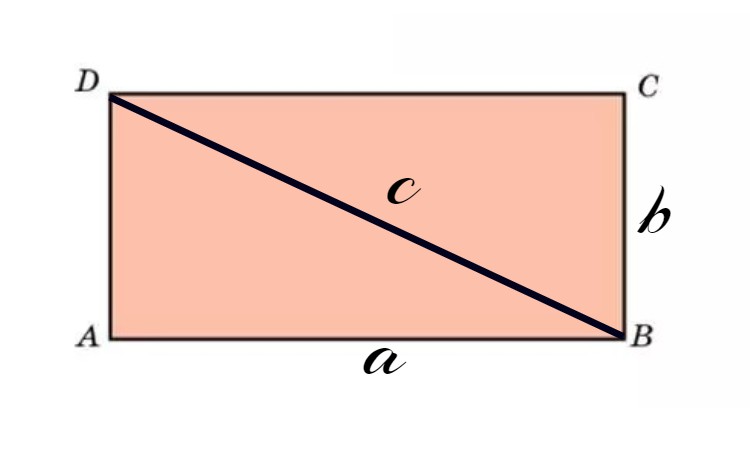
Научитесь использовать теорему Пифагора — она позволяет найти длину стороны прямоугольного треугольника, если известны длины двух других сторон. Можно использовать ее для нахождения гипотенузы, самой длинной из сторон треугольника, а также длины и ширины, образующих прямой угол.
- Прямоугольник имеет четыре прямых угла, и его диагональ образует два прямоугольных треугольника, так что мы можем использовать теорему Пифагора.
- Теорема Пифагора звучит так: квадрат гипотенузы равен сумме квадратов катетов, то есть a^2 + b^2 = c^2, где a и b — стороны (катеты) прямоугольного треугольника, а с — гипотенуза, самая длинная сторона.
2
Используйте теорему Пифагора для нахождения другой стороны треугольника. К примеру, прямоугольник имеет сторону длиной 6 см и диагональ длиной 10 см. Одна сторона — 6 см, другая — b, гипотенуза — 10 см. Вставьте значения в теорему и решите. Вот, как это делается:
- Пример: 6^2 + b^2 = 10^2
- 36 + b^2 = 100
- b^2 = 100 — 36
- b^2 = 64
- квадратный корень (b) = квадратный корень (64)
- b = 8
  - Длина другой стороны треугольника, которая также является другой стороной прямоугольника, — 8 см.
3
Найдите площадь прямоугольника. Поскольку для нахождения длины и ширины мы использовали теорему Пифагора, все, что нам нужно, — это помножить длину на ширину:
- Пример: 6 cм * 8 cм = 48 cм^2
4

Запишите окончательный ответ в квадратных единицах: 48 cм^2 или 48 кв. см.

Реклама

Советы

Все квадраты — прямоугольники, но не все прямоугольники — квадраты.
При нахождении площади ответ всегда нужно записывать в квадратных единицах.

Об этой статье

Эту страницу просматривали 279 981 раз.

Была ли эта статья полезной?

Источник

На уроках геометрии проходят множество новых тем, одна из них – это как найти площадь прямоугольника. После усвоения формул даются задачи для закрепления материала. В этой статье мы узнаем, как можно найти площадь прямоугольника и рассмотрим некоторые примеры по данной тематике.

Содержание

Как найти площадь прямоугольника – что представляет собой прямоугольник?
Площадь прямоугольника – базовая формула
Доказательство базовой формулы площади прямоугольника
Площадь прямоугольника – примеры расчета
Видео: Площадь прямоугольника – геометрия

В школе не все способны усвоить материал, который рассказывает преподаватель на уроке. Потому дома следует еще потренироваться и изучить то, что было непонятно на уроке. Иначе в дальнейшем пропущенные темы не усвоятся в голове ученика и будут большие пробелы в знаниях. Формулы следует знать наизусть, так вы сможете с легкостью решать задачи по геометрии. Как найти площадь прямоугольника – узнаем дальше.

Как найти площадь прямоугольника – что представляет собой прямоугольник?

Прежде чем начать изучение основного материала, следует разобраться, что такое за фигура прямоугольник. Благодаря таким знаниям будет понятно, как можно найти его площадь. Итак, фигура с четырьмя прямыми углами и равными противоположными сторонами – называется прямоугольником. Как видно из правила, что у прямоугольника все углы равны 90º и противоположные стороны между собой равны. Данное утверждение будет применяться для доказательств неких теорем. Причем длинные стороны прямоугольника – это длина фигуры, а те стороны, которые меньше — представляют собой высоту.

Площадь прямоугольника

ВАЖНО: Не все фигуры с четырьмя углами могут быть прямоугольниками.

И у прямоугольников есть определенные свойства, которые их характеризуют, в частности:

Стороны, которые находятся напротив друг друга между собой параллельны.
Линии, проведенные от противоположных углов прямоугольника – диагонали имеют одинаковую длину, а точка пересечения делит их на равные отрезки.
Еще эта точка в прямоугольнике называется – центром, относительно ее симметричны. Все другие точки, что находятся на одинаковом расстоянии друг от друга.
Не стоит также путать прямоугольник с параллелограммом и квадратом. У первого углы не 90º, а у второго абсолютно все стороны равны. Можно также сказать, что прямоугольник – это квадрат и параллелограмм, он подходит под некие характеристики этих фигур.

Площадь прямоугольника – базовая формула

Если свойства прямоугольника уже пройдены, то можно приступать и к изучению формул. Площадь прямоугольника рассчитывается по формуле:

S = a • b и измеряется в квадратных единицах.

Где S – это и есть площадь, а стороны, точнее длина и высота фигуры – это: a и b.

К примеру, прямоугольник AMNK с длиной MN = 8 см и высотой AM = 5 см будет иметь площадь:

S = MN • AM = 8 • 5 = 40 см²

Прямоугольник, площадь

Доказательство базовой формулы площади прямоугольника

Площадь прямоугольника является определенной величиной, которая показывает, сколько требуется места для данной фигуры на плоскости. Если геометрическую фигуру разбить на небольшие зоны величиной один на один сантиметр, как на изображении ниже, то легко можно высчитать значение площади в сантиметрах квадратных.

Прямоугольник. Как рассчитать площадь?

В прямоугольнике, что выше на картинке всего имеется 15 квадратов. То есть его площадь равна 15 см². И по рисунку видно, чтобы узнать это количество квадратов, следует умножить их число по горизонтали, на число их по вертикали:

5 • 3 = 15 см², а числа 5 и 3 – это стороны прямоугольника.

ВАЖНО: При расчетах все мерки необходимо выражать обязательно в одинаковых единицах меры, то есть если длина выражена в дециметрах или сантиметрах, то и высота выражается в дециметрах или же сантиметрах. А площадь тогда будет выражаться в квадратных единицах.

Площадь прямоугольника – примеры расчета

Площадь прямоугольника можно рассчитывать разными вариантами. В задачах даются определенные данные и их следует подставлять во все формулы, которые изучали до этого, чтобы находить необходимую величину. Давайте рассмотрим один из них. Если в задаче дана длина одной стороны и диагональ прямоугольника, то чему в таком случае будет равняться площадь прямоугольника? Здесь пригодится знание теоремы Пифагора.

Эта теорема о сторонах прямоугольного треугольника. Ее же можно применять и для нахождения сторон в прямоугольнике. Ведь, если известны две величины, то третью уже можно найти, зная предыдущие формулы геометрии. Про углы сейчас речь не будет идти, разберемся сначала со сторонами.

Теорема Пифагора представляет собой простейшее уравнение. В ней говорится, что гипотенуза в квадрате треугольника (или же еще она является самой длинной стороной прямоугольного треугольника), равна сумме квадратов катетов. Уравнение простейшее и записывать его можно так:

b² + a² = c², где обратите внимание, что c – кроме того, что гипотенуза, а еще и диагональ прямоугольника, а отрезки a и b – это стороны прямоугольника и катеты прямоугольного треугольника.

Рассмотрим конкретный пример, чтобы уяснить, как вычислить площадь прямоугольника, когда известны одна сторона, допустим a = 8 сантиметров и диагональ с = 10 сантиметров. Если прямоугольник разбить на два равных прямоугольных треугольника, то вы запросто найдете по теореме Пифагора, чему равен второй катет или сторона фигуры. А уже по этим данным можно найти и саму площадь прямоугольника.

Итак:

c² = b² + a²
b² = c² — a²
b² = 100 — 64
b² = 36
b = 6 сантиметров

Когда у прямоугольника известны стороны, то можно применить формулу площади прямоугольника для нахождения ее величины:

S = 6 • 8 = 48 квадратных сантиметров.

Площадь фигуры. Выводы

На примере видно, что площадь можно находить всяческими методами, главное знать формулы и свойства предыдущих занятий по геометрии и умело их применять на деле.

Видео: Площадь прямоугольника – геометрия

Источник

Выбирайте формулу, ориентируясь на известные величины.

1. Если известны две соседние стороны

Просто перемножьте две стороны прямоугольника.

S — искомая площадь прямоугольника;
a и b — соседние стороны.

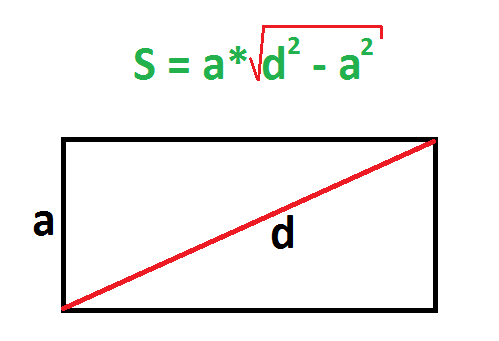
2. Если известны любая сторона и диагональ

Найдите квадраты диагонали и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте длину известной стороны на полученное число.

S — искомая площадь прямоугольника;
a — известная сторона;
d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).

3. Если известны любая сторона и диаметр описанной окружности

Найдите квадраты диаметра и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте известную сторону на полученное число.

S — искомая площадь прямоугольника;
a — известная сторона;
D — диаметр описанной окружности.

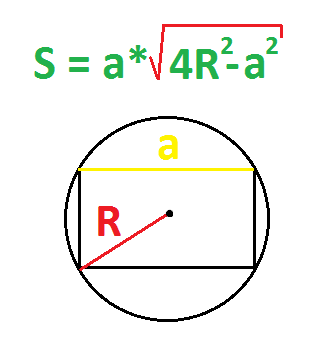
4. Если известны любая сторона и радиус описанной окружности

Найдите квадрат радиуса и умножьте результат на 4.

Отнимите от полученного числа квадрат известной стороны.

Найдите корень из результата и умножьте на него длину известной стороны.

S — искомая площадь прямоугольника;
a — известная сторона;
R — радиус описанной окружности.

5. Если известны любая сторона и периметр

Умножьте периметр на длину известной стороны.

Найдите квадрат известной стороны и умножьте полученное число на 2.

От первого произведения отнимите второе и разделите результат на 2.

S — искомая площадь прямоугольника;
a — известная сторона;
P — периметр прямоугольника (равен сумме всех сторон).

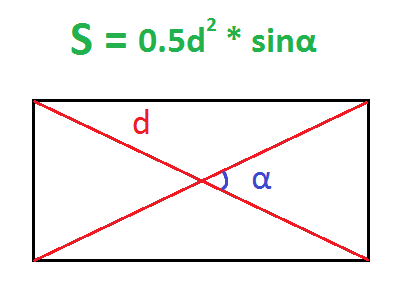
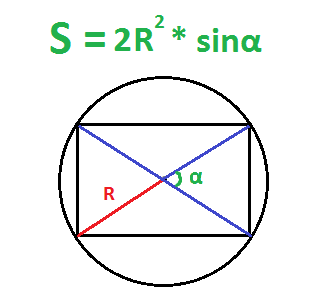
6. Если известны диагональ и угол между диагоналями

Найдите квадрат диагонали.

Разделите полученное число на 2.

Умножьте результат на синус угла между диагоналями.

S — искомая площадь прямоугольника;
d — любая диагональ прямоугольника;
α — любой угол между диагоналями прямоугольника.

7. Если известны радиус описанной окружности и угол между диагоналями

Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.

Умножьте полученное число на 2, а потом на синус угла между диагоналями.

S — искомая площадь прямоугольника;
R — радиус описанной окружности;
α — любой угол между диагоналями прямоугольника.

Что такое прямоугольник

Давайте не будем «срезать углы». Чтобы иметь возможность вычислить площадь прямоугольника, естественно, что мы сначала знаем, что это такое. Поэтому для начала необходимо помнить, что прямоугольник является четырехугольником. Другими словами, это геометрическая фигура, которая имеет четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Две самые длинные стороны представляют его длину, а две другие стороны представляют его ширину.

Не все четырехугольники являются прямоугольниками. Действительно, обязательно, чтобы они имели следующие свойства, чтобы мы могли сказать, что это действительно прямоугольник:

Характеристики прямоугольника

Противоположные стороны должны быть параллельны.

Диагонали прямоугольника должны быть одинаковой длины. Они также пересекаются в своей середине.
Точка пересечения диагоналей прямоугольника называется центром симметрии.
Кроме того, прямоугольник также является параллелограммом, так как его стороны попарно параллельны. Однако это частный случай параллелограмма. На самом деле он имеет четыре прямых угла, и его две параллельные стороны не должны иметь одинаковую длину. В противном случае все четыре стороны имеют одинаковую длину — тогда мы говорим о квадрате.

Формула площади прямоугольника

Как рассчитать площадь прямоугольника? Обратите внимание, что базовую формулу для вычисления площади (или площади) прямоугольника очень легко запомнить. Вы просто должны умножить его длину на ширину.

Площадь прямоугольника равна его длине, умноженной на ширину.

Например, площадь прямоугольника длиной 4 сантиметра и шириной 2 сантиметра равна 4 x 2 = 8 см².

Найти площадь прямоугольника по известным длине и ширине — онлайн калькулятор.

Площадь прямоугольника:

Диагональ прямоугольника:

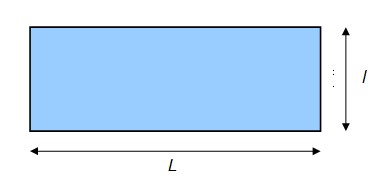
Площадь поверхности прямоугольника длиной L и шириной l равна: S = L x l

Принцип расчета площади прямоугольника

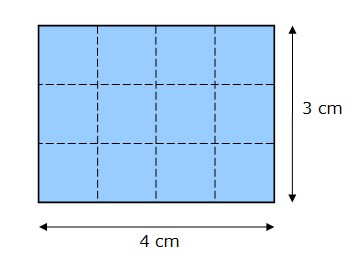
Чтобы вычислить площадь прямоугольника, мы посчитаем количество единиц областей, которые содержит прямоугольник:

В прямоугольнике выше 12 квадратов по 1 см². Его площадь составляет 12 см² (4 х 3).

Примечание. В этом расчете длина L и ширина l прямоугольника должны быть выражены в одной и той же единице длины. Результат будет выражен в той же единице измерения, возведенной в квадрат. Например, если длина прямоугольника выражена в метрах, ширина также должна быть выражена в метрах, а результат формулы для расчета площади прямоугольника даст результат в квадратных метрах (м²).

Площадь прямоугольника эквивалентна его территории. Территория — это термин, используемый для обозначения меры площади земли (мы используем единицу измерения гектар, а не м²). Гектар — это метрическая мера земельной площади, равная 10 000 м².

Пример расчета

Рассмотрим прямоугольник длиной L = 4 см и шириной l = 2 см. Площадь S его поверхности равна:

A = L x l = 4 x 2 = 8 см².

Как рассчитать площадь прямоугольника, если мы знаем только одну сторону и диагональ

Можно определить площадь прямоугольника другим способом. Формула, которая была изложена ранее, не является единственным методом, который можно использовать. Действительно, вполне возможно сделать это по-другому. Для этого нам нужно будет, по крайней мере, измерить только одну сторону и необходимо знать длину диагонали. В этом случае мы делаем расчет, используя теорему Пифагора.

Что такое теорема Пифагора

Это формула, которая используется для определения длины третьей стороны прямоугольного треугольника, когда вы уже знаете значение двух других его сторон.

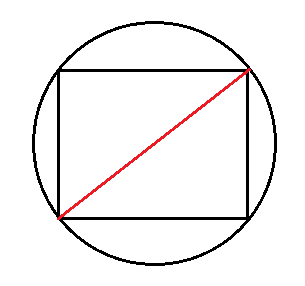
Обратите внимание, что прямоугольник состоит из двух прямоугольных треугольников. Действительно, диагональ представляет гипотенузу этого типа треугольника.

Теорема Пифагора

Кроме того, это также самая длинная сторона, которую можно найти на рисунке. Длина и ширина, с другой стороны, представляют две другие его стороны (скажем, смежные стороны). Это причина, почему можно использовать эту формулу для определения площади прямоугольника.

Теорема Пифагора основана на довольно простом уравнении, которое выглядит следующим образом: a² + b² = c². Где a и b используются для представления двух соседних сторон — катетов прямоугольного треугольника, а c представляет гипотенузу треугольника.

Чтобы полностью понять использование этой формулы, мы начнем с очень конкретного примера. Для этого предположим, что диагональ прямоугольника 10 см, а другая сторона 6 см. Если мы ссылаемся на формулу a² + b² = c², следовательно, сторона «a» составляет 6 см, а гипотенуза «c» — 10 см. Теперь нам нужно просто заменить буквенные значения числовыми значениями, которые у нас есть. Что дает нам:

a² + b² = c²

6² + b² = 10²

b² = 10² — 6²

b² = 100 — 36

b² = 64

b= 8

Мы получаем длину смежной стороны прямоугольника «b», которая равна 8 см. Теперь мы можем рассчитать площадь прямоугольника:

S = 8 см х 6 см

Следовательно, S = 48 см².

Источник

Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.

11 478

Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.

По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

Найти квадрат диагонали, то есть умножить ее на саму себя.
Найти квадрат известной стороны.
Из квадрата диагонали вычесть квадрат стороны.
Найти квадратный корень получившейся разности.
Умножить его на известную сторону.

Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

Квадрат стороны = 3*3 = 9 см.
Квадрат диагонали = 5*5 = 25 см.
Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
Умножаю корень разности на известную сторону: 16*9 = 144 см.

Ответ: 144 см.

Обратите внимание

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

По стороне и диаметру описанной окружности

Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

Действия:

Найдите квадрат диаметра – умножьте диаметр на диаметр.
Найдите квадрат известной стороны.
Отнимите от квадрата диаметра квадрат стороны.
Найдите квадратный корень разности.
Умножьте квадратный корень на известную сторону.

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

Квадрат диаметра: 10*10 = 100 см.
Квадрат стороны: 8*8 = 64 см.
Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
Умножаю сторону на корень из разности: 8*6 = 48 см.

Ответ: 48 см.

Лайфхак

Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

Другой способ:

Найти квадрат радиуса (умножьте радиус на радиус).
Умножить квадрат радиуса на 4.
Найти квадрат известной стороны.
Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
Найти квадратный корень разности.
Умножить корень на известную сторону.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

Квадрат радиуса: 5*5=25 см.
Четыре квадрата радиуса: 4*25 = 100 см.
Квадрат стороны: 6*6 = 36 см.
Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
Нахожу квадратный корень разности. Корень из 64 равен 8 см.
Умножаю корень на сторону: 8*6 = 48 см.

Ответ: 48 см.

Помните

Радиус = половине диаметра.

Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

По стороне и периметру – 1 способ

Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.

Нахожу вторую сторону прямоугольника:
1. P=2(a+b).
2. P=2a+2b.
3. 14= 2*3+2b.
4. 14 = 6+2b.
5. 2b = 14-6 = 8.
6. b = 8/2.
7. b = 4.
Нахожу площадь по основной формуле. S = 3*4 = 12 см.

Ответ: 12 см.

По стороне и периметру – 2 способ

Действия такие:

Умножьте периметр на сторону.
Найдите квадрат стороны.
Умножьте квадрат стороны на 2.
Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
Поделите на 2.

Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

Умножаю периметр на сторону: 8*28 = 224 см.
Нахожу квадрат стороны: 8*8 = 64 см.
Умножаю квадрат стороны на два: 64*2 = 84 см.
Отнимаю из первого третье: 224-84 = 140 см.
Делю разность на два: 140/2 = 70 см.

Ответ: 70 см.

По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

Действия:

Найти квадрат диагонали (умножить диагональ на саму себя).
Найти половину этого квадрата – умножить его на 0,5.
Найти синус угла между диагоналями.
Умножить половину квадрата диагонали на синус угла между диагоналями.

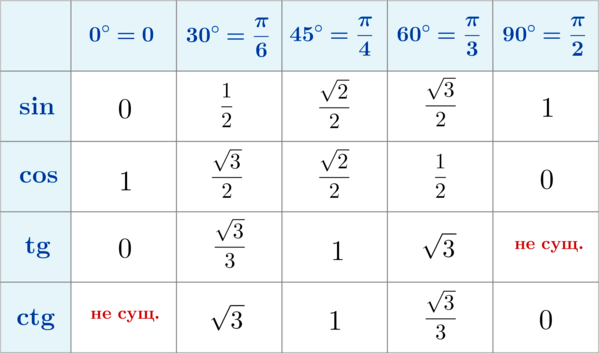
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

Квадрат диагонали: 10*10 = 100 см.
Половина этого квадрата: 0,5*100 = 50 см.
Синус угла между диагоналями: sin 30 градусов = 0,5.
Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.

Ответ: 25 см.

Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

По радиусу описанной окружности и углу между диагоналями – первый способ

Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.

Находим длину диагонали: 6*2 =12 см.
Квадрат диагонали равен 144 см.
Половина квадрата: 72 см.
Синус 30 градусов равен 0,5.
Умножаем половину квадрата на синус: 72*0,5 = 36 см.

Ответ: 36 см.

По радиусу описанной окружности и углу между диагоналями – второй способ

Действия:

Найти квадрат радиуса (умножить радиус на радиус).
Умножить квадрат радиуса на два.
Найти синус угла между диагоналями.
Умножить синус угла на два радиуса в квадрате.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.

Квадрат радиуса: 6*6 = 36.
Два радиуса в квадрате: 36*2 = 72.
Синус 30 градусов равен 0,5.
Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.

Ответ: 36 см.

Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.

( 1 оценка, среднее 5 из 5 )

Оцените статью

ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА

Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети

Источник