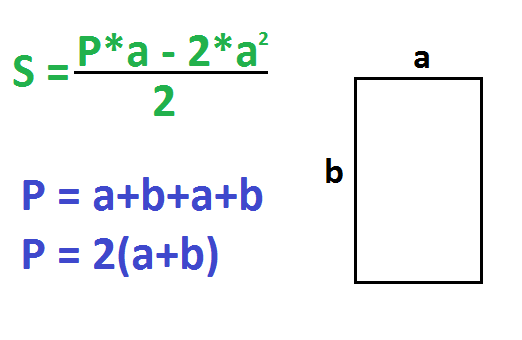Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
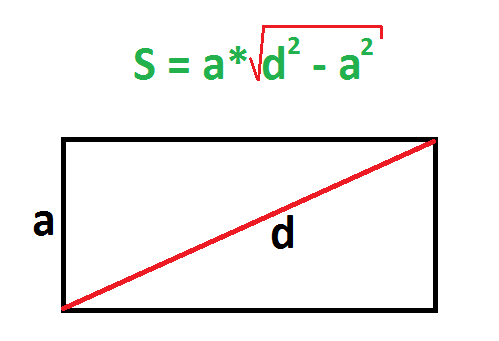
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
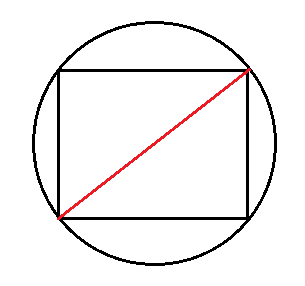
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
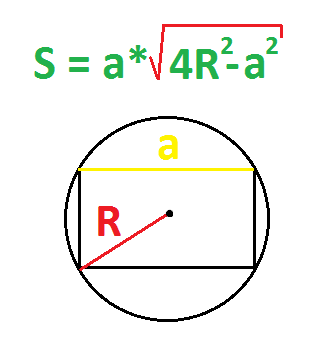
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
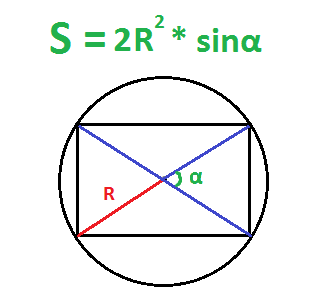
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
Площадь прямоугольника через диагональ
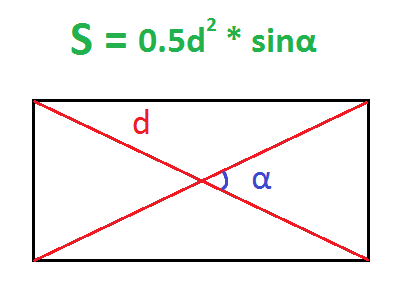
В прямоугольнике диагонали равны между собой. Если известен угол α между диагоналями (длина диагоналей равна d), то площадь прямоугольника можно найти по формуле:
Sпр = 0,5 * d² * sinα.
Например, если угол между диагоналями равен 30°, а диагонали равны 5 см, то площадь будет равна:
Sпр = 0,5 * 25 * 0,5 = 6,25 см.
Если неизвестен угол между диагоналями, то будет нужно найти стороны прямоугольника. А затем воспользоваться формулой:
Sпр = a * b.
Как известно, диагональ прямоугольника делит его на 2 равных прямоугольных треугольника. Поэтому задача сводится к тому, чтобы найти катеты прямоугольного треугольника через гипотенузу.
Кроме длины диагонали требуется знать либо одну из сторон прямоугольника, либо отношение сторон, либо угол между стороной и диагональю.
1) Если известна диагональ (пусть она будет равна d) и одна из сторон (например, b), то выражаем неизвестную сторону из формулы:
a² + b² = c² -> a = √(c² — b²).
Sпр = a * b = √(c² — b²) * b.
Например, если диагональ d = 5 см и сторона b = 3 см, то a = √(25 — 9) = √16 = 4 см.
Площадь прямоугольника равна 3 * 4 = 12 см.
2) Если известно отношение сторон, то задача сводится к нахождению обеих сторон через составление уравнения.
Например, если стороны относятся как 2:3, а диагональ равна 13 см, то можно составить уравнение:
(2x)² + (3x)² = 4x² + 9x² = 169.
13x² = 169.
x = √13.
Значит, a = 2√13 см и b = 3√13 см.
Площадь прямоугольника равна 2√13 * 3√13 = 6 * 13 = 78 см.
3) Если известна диагональ и один из прилежащих к диагонали углов, то нужно воспользоваться формулами:
a = d * cosβ (β — прилежащий угол) и b = d * sinα (α — противолежащий угол).
Например, d = 10 см и угол α = 30°.
a = 10 * cos30° = 10√3 / 3.
b = 10 * sin30° = 5 см.
Площадь прямоугольника равна 5 * (10√3 / 3) ≈ 28,33 см.
Калькулятор площади прямоугольника
Рассчитайте онлайн площадь прямоугольника, зная его стороны или диагонали.
Что известно
Размерность
Сторона 1
см
Сторона 2
см
Диагональ
см
Угол
гр.
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🧮 Калькулятор для расчета площади прямоугольника
Калькулятор площади прямоугольника — это онлайн инструмент, который помогает вычислить площадь прямоугольника. Для вычисления площади прямоугольника необходимо умножить длину на ширину. Формула вычисления площади прямоугольника:
S = a x b
где S — площадь прямоугольника, a — длина прямоугольника, b — ширина прямоугольника.
Калькулятор площади прямоугольника обычно позволяет ввести значения длины и ширины прямоугольника и автоматически вычисляет его площадь. Это может быть полезно для решения задач по геометрии или при необходимости быстрого расчета площади прямоугольной поверхности.
С нашим калькулятором площадь прямоугольника можно рассчитать не только используя значение длины и ширины, но и через диагонали и угол между ними. Формула будет выглядеть следующим образом:
S = 0,5 × d2 × 𝑠𝑖𝑛(𝑎)
где S — площадь прямоугольника, d — длина диагоналей прямоугольника, α — угол между диагоналями.
Для чего можно использовать такой калькулятор?
Калькулятор площади прямоугольника может быть полезен в различных ситуациях, например:
- При решении задач по геометрии, связанных с прямоугольниками.
- При выполнении строительных работ, когда необходимо вычислить площадь прямоугольного участка земли или поверхности для проведения работ.
- При работе в области дизайна интерьера и мебели, где необходимо вычислить площадь прямоугольных поверхностей для расчета материалов или определения размеров мебели.
- В учебных целях, чтобы лучше понимать связь между диагоналями, углами и площадью прямоугольника.
Калькулятор площади прямоугольника может значительно упростить и ускорить процесс вычисления площади.
Пример
Допустим, у вас есть комната прямоугольной формы, и вы хотите вычислить ее площадь для того, чтобы определить количество краски, необходимое для ее покраски.
Для этого необходимо измерить длину и ширину комнаты с помощью измерительной ленты. Предположим, что длина комнаты составляет 6 метров, а ширина — 4 метра.
Затем можно воспользоваться калькулятором площади прямоугольника, введя значения длины и ширины комнаты в соответствующие поля. Калькулятор автоматически вычислит площадь комнаты, которая в данном случае составляет 24 квадратных метра.
Таким образом, зная площадь комнаты, можно определить, сколько краски понадобится для ее покраски, используя информацию о расходе краски на квадратный метр поверхности. Такой расчет может быть полезен, если вы собираетесь сделать ремонт в своей квартире или доме.
❓Вопросы и ответы
Несколько вопросов и ответы на них по калькулятору площади прямоугольника:
Что такое площадь прямоугольника?
Площадь прямоугольника — это мера, определяющая, сколько плоской поверхности занимает данный прямоугольник.
Для чего нужен калькулятор площади прямоугольника?
Калькулятор площади прямоугольника может использоваться во многих ситуациях, например, при строительных работах, в дизайне интерьера, при решении задач по геометрии и в повседневной жизни.
Что такое диагональ прямоугольника?
Диагональ прямоугольника — это отрезок, соединяющий противоположные вершины прямоугольника.
Что такое прямоугольник?
Прямоугольник — это геометрическая фигура, которая имеет четыре угла, все из которых прямые (равны 90 градусам), и противоположные стороны параллельны друг другу и имеют равные длины.
По определению, прямоугольник является частным случаем параллелограмма, у которого все углы прямые.
Можно ли использовать такой калькулятор для измерения площади других четырехугольников?
Нет, калькулятор площади прямоугольника может быть использован только для измерения площади прямоугольника, который имеет две параллельные стороны и все углы равны 90 градусов.
Для измерения площади других четырехугольников, таких как квадрат, ромб, трапеция, параллелограмм или прямоугольная трапеция, необходимо использовать соответствующий калькулятор для каждой фигуры, который учитывает специфические формулы и свойства этих фигур.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
11 455
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
- Найти квадрат диагонали, то есть умножить ее на саму себя.
- Найти квадрат известной стороны.
- Из квадрата диагонали вычесть квадрат стороны.
- Найти квадратный корень получившейся разности.
- Умножить его на известную сторону.
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
- Квадрат стороны = 3*3 = 9 см.
- Квадрат диагонали = 5*5 = 25 см.
- Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
- Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
- Умножаю корень разности на известную сторону: 16*9 = 144 см.
Ответ: 144 см.
Обратите внимание
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
По стороне и диаметру описанной окружности
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
Действия:
- Найдите квадрат диаметра – умножьте диаметр на диаметр.
- Найдите квадрат известной стороны.
- Отнимите от квадрата диаметра квадрат стороны.
- Найдите квадратный корень разности.
- Умножьте квадратный корень на известную сторону.
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
- Квадрат диаметра: 10*10 = 100 см.
- Квадрат стороны: 8*8 = 64 см.
- Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
- Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
- Умножаю сторону на корень из разности: 8*6 = 48 см.
Ответ: 48 см.
Лайфхак
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
Другой способ:
- Найти квадрат радиуса (умножьте радиус на радиус).
- Умножить квадрат радиуса на 4.
- Найти квадрат известной стороны.
- Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
- Найти квадратный корень разности.
- Умножить корень на известную сторону.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
- Квадрат радиуса: 5*5=25 см.
- Четыре квадрата радиуса: 4*25 = 100 см.
- Квадрат стороны: 6*6 = 36 см.
- Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
- Нахожу квадратный корень разности. Корень из 64 равен 8 см.
- Умножаю корень на сторону: 8*6 = 48 см.
Ответ: 48 см.
Помните
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
- Нахожу вторую сторону прямоугольника:
- P=2(a+b).
- P=2a+2b.
- 14= 2*3+2b.
- 14 = 6+2b.
- 2b = 14-6 = 8.
- b = 8/2.
- b = 4.
- Нахожу площадь по основной формуле. S = 3*4 = 12 см.
Ответ: 12 см.
По стороне и периметру – 2 способ
Действия такие:
- Умножьте периметр на сторону.
- Найдите квадрат стороны.
- Умножьте квадрат стороны на 2.
- Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
- Поделите на 2.
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
- Умножаю периметр на сторону: 8*28 = 224 см.
- Нахожу квадрат стороны: 8*8 = 64 см.
- Умножаю квадрат стороны на два: 64*2 = 84 см.
- Отнимаю из первого третье: 224-84 = 140 см.
- Делю разность на два: 140/2 = 70 см.
Ответ: 70 см.
По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
Действия:
- Найти квадрат диагонали (умножить диагональ на саму себя).
- Найти половину этого квадрата – умножить его на 0,5.
- Найти синус угла между диагоналями.
- Умножить половину квадрата диагонали на синус угла между диагоналями.
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.
- Квадрат диагонали: 10*10 = 100 см.
- Половина этого квадрата: 0,5*100 = 50 см.
- Синус угла между диагоналями: sin 30 градусов = 0,5.
- Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.
Ответ: 25 см.
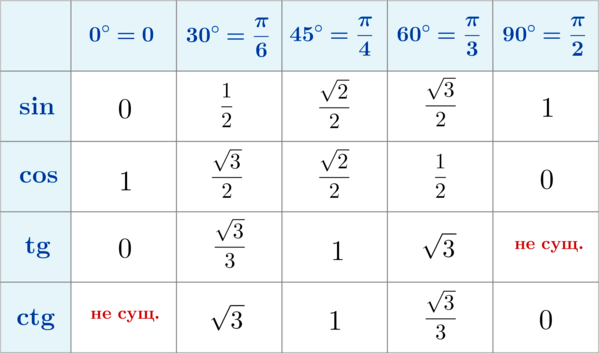
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
- Находим длину диагонали: 6*2 =12 см.
- Квадрат диагонали равен 144 см.
- Половина квадрата: 72 см.
- Синус 30 градусов равен 0,5.
- Умножаем половину квадрата на синус: 72*0,5 = 36 см.
Ответ: 36 см.
По радиусу описанной окружности и углу между диагоналями – второй способ
Действия:
- Найти квадрат радиуса (умножить радиус на радиус).
- Умножить квадрат радиуса на два.
- Найти синус угла между диагоналями.
- Умножить синус угла на два радиуса в квадрате.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
- Квадрат радиуса: 6*6 = 36.
- Два радиуса в квадрате: 36*2 = 72.
- Синус 30 градусов равен 0,5.
- Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.
Ответ: 36 см.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
( 1 оценка, среднее 5 из 5 )
Оцените статью
ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА
Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети
ПОДПИСАТЬСЯ
Формула площади прямоугольника через диагональ

4.8
Средняя оценка: 4.8
Всего получено оценок: 217.
4.8
Средняя оценка: 4.8
Всего получено оценок: 217.
Все с начальной школы знают формулу площади прямоугольника. Площадь прямоугольника равняется произведению длины на ширину. Но иногда бывает, что узнать длину или ширину не представляется возможным, зато есть значения диагоналей.
Определения
Поговорим о нескольких определениях, которые необходимы для того, чтобы разобраться в этой теме.
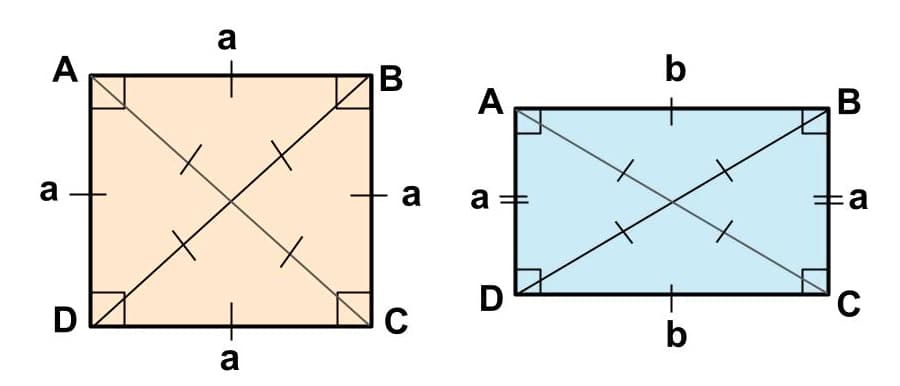
Прямоугольник – это выпуклый четырехугольник, стороны которого попарно равны и параллельны, а углы равняются 90 градусам. Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны между собой.
Что такое диагональ? Диагональ – это отрезок, который соединяет противолежащие стороны фигуры. Диагональ существует во всех фигурах, число вершин которых больше 3.
У треугольника диагоналей нет, а у тетраэдра или додекаэдра есть.
Четырехугольники подразделяются на выпуклые и невыпуклые. Выпуклые четырех угольники определяют по следующему правилу: через любые две соседние вершины фигуры проводят прямую. Если фигура лежит по одну сторону от прямой, то четырехугольник выпуклый, если нет – невыпуклый. Все известные четырехугольники являются выпуклыми.
Формула площади прямоугольника
Площадь прямоугольника обычно определяют как произведение длины на ширину. Эта формула выводится через разделение фигуры диагональю на два прямоугольных треугольника. Площадь каждой из фигур это половина произведения катетов. Общая площадь двух фигур целое произведение катетов. Этими катетами как раз и являются длина и ширина прямоугольника.
Но случаются ситуации, когда приходится искать площадь, но значений длины или ширины нет. Что делать тогда? Воспользоваться общей для всех четырех угольников формулой и найти площадь прямоугольника через диагонали.
Площадь любого выпуклого четырех угольника равняется произведению диагоналей на синус угла между ними. Диагонали прямоугольного треугольника равны между собой, поэтому значения угла и одной диагонали хватит для нахождения площади.
$$S={1over2}*d^2*sin(a)$$
Внимательно следите за тем, какой именно угол дан в условиях задачи. Необходим острый угол при диагоналях. Если тупой, то можно воспользоваться формулой смежного угла. Если дан какой-либо из углов между стороной и диагональю, то придется искать другие пути решения.
Возможны ситуации, когда нужно найти площадь, а известен угол между диагональю и стороной и значение диагонали и стороны. Тогда нужно найти площадь прямоугольного треугольника через формулу с применением синуса и удвоить ее.
В этом случае площадь прямоугольника будет равна:
S=d*b*sin(a)
Что мы узнали?
Мы поговорили о площади прямоугольного треугольника. Выделили отдельно формулу площади прямоугольника через диагонали. Поговорили о случаях, когда применение этой формулы невозможно или затруднено и привели альтернативный вариант решения.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.8
Средняя оценка: 4.8
Всего получено оценок: 217.
А какая ваша оценка?