|
Площадь по заданным координатам. Как найти (вычислить) площадь фигуры (треугольник, четырехугольник, трапеция, многоугольник и др.) по координатам? Какие есть формулы и методы, позволяющие находить площадь через координаты? бонус за лучший ответ (выдан): 5 кредитов Для вычисления площади простого многоугольника с любым количеством вершин, представленных в виде списка координат, при последовательном обходе которых, не образуются пересекающиеся линии, применяется формула Гаусса, иначе называемая «формулой землемера», «формулой геодезиста», «формулой шнурования», «алгоритмом шнурования», а так же «методом треугольников». Суть метода заключается в построении треугольников, состоящих из сторон многоугольника и лучей проведённых из начала координат к вершинам многоугольника, и сложении площадей треугольников, включающих внутреннюю часть многоугольника с вычитанием площадей треугольников, расположенных снаружи. Площадь, вычисленная по приведенной формуле, будет иметь отрицательное значение при обходе фигуры по часовой стрелке и положительное при обходе против часовой стрелки. Фигура многоугольника может иметь произвольную геометрию. Например: Список координат многоугольника представлен в виде массива: (x1, y1), (x2, y2), (x3, y3),…(xn, yn). Для многоугольника на первом рисунке он задан точками: (3,4), (5,11), (12,8), (9,5), (5,6). Его площадь будет равна: Существует также метод трапеций, основанный на сложении и вычитании площадей трапеций, образованных каждой из сторон многоугольника, её проекцией на ось абсциссы и перпендикулярами, опущенных из вершин на абсциссу. При обходе вершин по часовой стрелке учитывается величина координаты вершин. Если первая вершина меньше второй, то площадь трапеции прибавляется, если нет, то отнимается. Для многоугольника ABCDE на левом нижнем рисунке существует 5 трапеций : ABJH, CBJF, CDIF, EDIG и EAHG. Так как X1<X2, X3<X4 и X5<X1, то площади трапеций ABJH, CDIF и EAHG складываются, а X3>X4 и X4<X5, следовательно, площади трапеций CBJF и EDIG вычитаются: S = S(ABJH) – S(CBJF) + S(CDIF) – S(EDIG) + S(EAHG) Площади трапеций рассчитываются по формуле; Sтрапеции = 1/2 *((a+b))*h, где a, b – основания трапеции, h – высота трапеции. Значения a, b и h вычисляются по координатам. В декартовых координатах круг может быть представлен двумя точками: центр А и любая точка В, лежащая на окружности. Для расчета площади круга необходимо вычислить его радиус по формуле: автор вопроса выбрал этот ответ лучшим Ксарфакс 5 лет назад Площадь фигуры по координатам вершинЕсли известны координаты всех вершин, то площадь заданной геометрической фигуры (треугольника, прямоугольника, трапеции, ромба и т.д) можно найти по стандартным формулам. Но предварительно нужно найти длину сторон, диагоналей и т.п. (всё зависит от фигуры) с помощью формулы нахождения длины отрезка по заданным координатам. Эта формула выглядит следующим образом: Здесь: AB — отрезок, точка A имеет координаты (x1, y1), точка B имеет координаты (x2, y2). Рассмотрим несколько примеров. 1) Треугольник ABC имеет координаты A(2,3); B(6,7); C(5,0). Его площадь можно найти по формуле Герона: Здесь: S — площадь треугольника, a, b, c — стороны, p — полупериметр, который равен половине суммы сторон a, b и c. Найдём, чему равны стороны треугольника по формуле нахождения длины отрезка по координатам: AB = √(4² + 4²) = √32 ≈ 5,66. AC = √(3² + (-3)²) = √18 ≈ 4,24. BC = √((-1)² + (-7)²) = √50 ≈ 7,07. Полупериметр треугольника будет равен (5,66 + 4,24 + 7,07) / 2 ≈ 16,97 / 2 ≈ 8,49. Отсюда площадь треугольника ABC ≈ √(8,49 * 2,83 * 4,25 * 1,42) ≈ √145 ≈ 12,04. 2) Ромб ABCD имеет координаты A(1,2); B(3,4); C(5,2); D(3,0). Площадь можно найти через диагонали: Здесь: S — площадь ромба, d1 и d2 — диагонали. Таким образом, нам нужно найти диагонали AC и BD. AC = √(4² + 0) = √16 = 4. BD = √(0 + (-4)²) = √16 = 4. Отсюда площадь ромба ABCD = 0,5 * 4 * 4 = 8. 3) Трапеция ABCD имеет координаты A(1,1); B(3,4); C(5,4); D(6,1). Стандартная формула площади трапеции такая: Здесь: S — площадь трапеции, a и b — основания, h — высота. Высота трапеции (пусть это будет BE) — это перпендикуляр, который был опущен из вершины трапеции (из точки B) на её основание (в нашем случае это AD). Определим координаты её отрезка:
Высота трапеции BE = √(0 + (-3)²) = √9 = 3. Теперь посчитаем длину оснований: BC = √(2² + 0) = √4 = 2. AD = √(5² + 0) = √25 = 5. Таким образом, площадь трапеции ABCD = 3 * 0,5 * (2 + 5) = 10,5. Степан-16 6 лет назад Первоначально нужно вычислить длины сторон. В этом здесь будет основная задача. Получив стороны, вычисляем площади по стандартным формулам. Самый простой случай — для прямоугольника, когда его стороны параллельны осям координат. Тогда одна сторона будет равна разнице абсцисс, вторая ординат. Треугольник. Допустим, основание параллельно оси абсцисс. Вычисляем его длину, как разницу абсцисс. Далее нужно найти высоту. Она будет равна разнице ординат третьей вершины и ординаты любой из вершин основания. Затем — площадь по формуле: половина произведения основания на высоту. И т.д. Если же стороны фигуры не параллельны осям, то находить длины сторон придется уже более сложными расчетами. Допустим, прямоугольник. Первую сторону будем искать, как если бы она была гипотенузой в составе прямоугольного треугольника. Каждая сторона будет равна квадратному корню из суммы квадратов абсцисс и ординат концов отрезков стороны. Так и для любой фигуры. Вначале определяем длины сторон как гипотенузу треугольника. После чего применяем стандартные формулы площадей. Эления 3 года назад Рассчитать площадь какой угодно геометрической фигуры, зная координаты, не составляет сложности. Каждая из точек, соответствующая вершинам искомой фигуры, будь это треугольник, четырех- или многоугольник, имеет определенную координату, а значит у нее есть значение, через которое можно рассчитать площадь. Координаты, как найти на графике, чтобы узнать площадь фигуры? Проецируем на оси абсцисс и ординат прямые, проведя перпендикуляр из каждой точки. Полученные значения будут исходной величиной. Каждая из сторон фигуры — это разница двух точек на горизонтальную и вертикальную оси. Разница между значениями означает длину стороны фигуры. А зная все стороны и их значение, по формуле находим площадь. Пример 1. Ищем площадь треугольника. Мы видим два отрезка зеленого цвета AB и BC, которые образуют стороны равнобедренного треугольника, а основание есть отрезок на оси абсцисс AC. Даны значения: AC основание в промежутке от «-4» до «+4», то есть длина основания равна восьми. Будет лучше, если посчитать площадь этого треугольника, как сумму из образовавших его двух треугольников, которые являются прямыми, ABO и BOC, совпадающие прямым углом с координатой «0» на графике. Известна длина каждй из сторон, образующих прямой угол (AO или OC) х = 4 — 0 = 4 и y = 2 — 0 = 2 (BO). Зная длину двух сторон, образующих прямой угол (AO и BO), находим длину основания (AB или BC). Тогда уже знаем все длины каждой из сторон обоих прямых треугольников. Остается только найти площадь по формуле: Зная площадь каждого из прямых треугольников, умножаем на два, получаем сумму заштрихованного треугольника на графике ABC. И еще математически можно записать решение следующим образом, исходя из того, что имеем изначально следующую систему неравенств: Пример 2. Пример 3. Есть парабола, ищем площадь фигуры, ограниченную кривой параболы. Чтобы посчитать, используем интеграл. Бекки Шарп 3 года назад Рассмотрим простой случай, где буквально на пальцах можно посчитать площадь через обычную формулу, а затем применим к этой задаче формулу Гаусса. У нас есть трапеция, у которой известны координаты вершин. (3:2) (5:2) (9:6) (6:6). Мы знаем, что площадь трапеции равна сумме оснований, деленной на 2 и умноженной на высоту. S = (a+b)/2 х h Считаем площадь: S = (3+2):2х4 = 10. Ответ — 10. А теперь по теореме Гаусса. Не смотря на страшный вид, формула очень простая. В квадратных скобках мы перемножаем абсциссу первой точки с ординатой второй, прибавляем абсциссу второй, умноженную на ординату третьей и так идем по кругу фигуры. Далее вычитаем ординату первой умноженную на абсциссу второй и т.д. В квадратных скобках у нас может получиться отрицательное число. S= 0,5 х [3х6+6х6+9х2+5х2 — 2х6-6х9-6х5-2х3] = 10 Таким образом можно найти площадь любой сложной фигуры, зная ее координаты. dydySacha 6 лет назад Можно взять милиметровку и нанести точки с заданными координатами, согласно осей абсцис и ординат. Соединить эти точки между собой и замерить длины образовавшихся сторон, а с помощью формулы по определению площади образовавшейся фигуры узнать её значение подставив данные в эту формулу. Алиса в Стране 3 года назад Существует специальная формула, называемая формулой Гаусса, она и позволит нам определить искомую площадь по координатам. Вот как эта формула выглядит: Формула выглядит немного устрашающе, но давайте попробуем в ней разобраться. У нас есть многоугольник и есть его координаты, подсчитать n — количество сторон многоугольника несложно, а дальше просто нужно подставлять значения в эту формулу, нужно только быть внимательным и не перепутать какие координаты куда надо писать. Давайте теперь приведем пример нахождения такой площади через формулу Гаусса. Допустим, у нас есть вот такой пятиугольник: Координаты его пяти вершин, как мы видим: (3, 4), (5, 11), (12, 8), (9, 5), (5, 6). Теперь нам остается только очень внимательно подставить эти координаты в нашу формулу, n = 5, координаты известны, вот что у нас получится: Когда разбираешься в этой формуле, понимаешь, насколько она проста и даже легко запоминается, несмотря на то, что сначала кажется очень сложной. duselldorf 5 лет назад Для вычисления площади геометрической фигуры по координатам ее вершин, нужно воспользоваться формулой Гаусса, иногда ее называют формулой землемера или формулой геодезиста, так как она применяется геодезистами для определения площади земельного участка, например, при межевании: где А — площадь многоугольника с заданными координатам его вершин, n — количество сторон многоугольника, (xi, yi) — координаты вершин многоугольника, i = 1, 2,…, n — номер вершины многоугольника. Бархатные лапки 3 года назад Находим площадь вот такого несложного четырехугольника. Координаты его вершин нам известны. Применяем формулу Гаусса, которая выглядит так: S (площадь) = 0,5 [6х4 +9х7 + 10х6 + 7х3 — 3х9 — 4х10 — 7х7 — 6х6] = 8 (квадратных единиц) Как видим если применять при решении формулу Гаусса то решить такую задачку несложно. Не вижу здесь серьезных проблем. Мы, как я понял, имеем готовые точки координат, которые нужно проставить на координатной плоскости. Далее, соединяя эти точки, получаем фигуру, как в примере вопроса — квадрат, треугольник и т.п. Теперь вычисляем площадь любой из полученных фигур по формуле ей соответствующей. Знаете ответ? |
Площади многоугольников на координатной сетке
5 февраля 2011
Многоугольники на координатной сетке — это самые простые задачи B5. Существует сразу несколько методов решения таких задачи, в том числе универсальный, описанный ниже. Для начала определимся с терминологией:
Многоугольник — фигура на плоскости, ограниченная замкнутой ломаной.
Большинство многоугольников, встречающихся в ЕГЭ, являются выпуклыми, т.е. не имеют внутренних углов размером больше 180°, а все вершины многоугольника лежат в узлах координатной сетки. Кроме того, ломаная, ограничивающая многоугольник, не имеет самопересечений. Все это значительно упрощает задачу.
Для решения всех задач этого типа достаточно выполнить четыре простых шага:
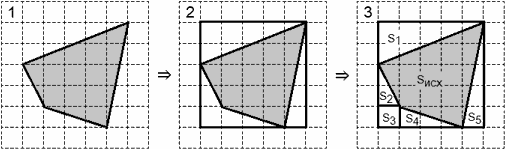
- Описать вокруг многоугольника прямоугольник, стороны которого параллельны осям координат (линиям сетки). При этом желательно, чтобы на каждой стороне прямоугольника присутствовала хотя бы одна вершина исходной фигуры;
- Разбить внутреннее пространство прямоугольника, не занятое исходной фигурой, на квадраты и треугольники. Лучше, если все линии разбиения будут параллельны осям координат;
- Найти площадь каждого элемента разбиения. Сложив эти площади, получим площадь всего разбиения;
- Наконец, из площади прямоугольника вычесть площадь разбиения — это и будет площадью исходной фигуры.
Несмотря на большое количество элементов разбиения, вычисление его площади — достаточно тривиальная задача.
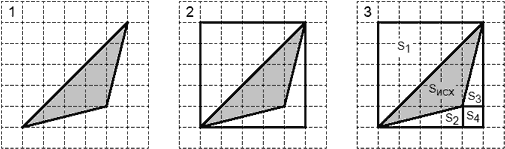
Проиллюстрируем каждый шаг решения:
Последним шагом найдем площадь исходной фигуры: Sисх = S − (S1 + S2 + S3 + S4 + S5), где S — площадь описанного прямоугольника. Осталось вычислить площадь большого прямоугольника и элементов разбиения. Эти несложные расчеты предлагается выполнить читателю в качестве упражнения.
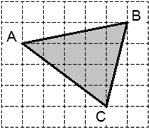
Задача. Найти площадь треугольника ABC, изображенного на рисунке:

Обозначение треугольника можно опустить, поскольку оно нам не потребуется. Приведем первые три шага:
Итак, Sисх = S − (S1 + S2 + S3), где S — площадь описанного прямоугольника. Найдем площадь элементов разбиения:
S1 = ½ · 1 · 5 = 2,5; S2 = ½ · 3 · 4 = 6; S3 = ½ · 1 · 4 = 2; S = 5 · 4 = 20.
Наконец, найдем площадь треугольника: Sисх = 20 − (2,5 + 6 + 2) = 9,5.
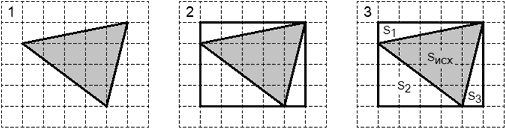
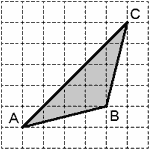
Задача. Найти площадь треугольника ABC, изображенного на рисунке:

Снова выполняем первые три шага. Заметим, что угол ABC — тупой, поэтому в разбиении присутствует квадрат. Имеем:
Очевидно, Sисх = S − (S1 + S2 + S3 + S4), где S — площадь описанного прямоугольника. Найдем площадь элементов разбиения:
S1 = ½ · 5 · 5 = 12,5; S2 = ½ · 4 · 1 = 2; S3 = ½ · 1 · 4 = 2; S4 = 1 · 1 = 1; S = 5 · 5 = 25.
Площадь треугольника: Sисх = 25 − (12,5 + 2 + 2 + 1) = 7,5.
Смотрите также:
- Задача B5: вычисление площади методом обводки
- Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
- Системы линейных уравнений: основные понятия
- Тест к уроку «Знаки тригонометрических функций» (1 вариант)
- Координаты вершин правильного тетраэдра
- Задача B2 про комиссию в терминале
По теме: методические разработки, презентации и конспекты
«Решение задач на вычисление площади прямоугольника»
Урок «Решение задач на вычисление площади прямоугольника», рассчитан на учащихся 5 класса….
Формулы для вычисления площади и периметра квадрата и прямоугольника.
Урок по математике для 5 класса по теме «Единицы измерение площадей». Тип урока: комплексное применение знаний и способов деятельности учащихся. Вид учебного занятия: урок − опрос с элемен…
Диагностический контроль материала по теме «Площадь. Площадь прямоугольника, квадрата. Единицы измерения площади».
Данный материал позволит проверить прочность знаний учеников 5 класса по данным темам….
Урок геометрии: «Вычисление площади прямоугольника».
Вычисление площади прямоугольника…
Технологическая карта урока по теме «Площадь. Площадь прямоугольника. Площадь квадрата» 5 класс
Урок по математике в 5 классе по теме «Площадь. Площадь прямоугольника. Тип урока — получение новых знаний….
Вычисление площадисложной фигуры, состоящей из прямоугольников (квадратов).
Совершенствование знаний и умений учащихся при вычислении площади сложных фигур путем деления их на части, площади прямоугольника, квадрата; уметь давать анализ заданий на вычисление площади “сл…
Понятие о площади плоской фигуры и её свойствах. Измерение площадей. Единицы измерения площади. Сравнение и вычисление площадей. Понятие площади многоугольника. Площадь многоугольника
Изучение новой темы….
Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту
Векторная алгебра
->
- Площадь фигуры по координатам
- Длина линии по координатам
- Координаты точки пересечения линий
- Площадь фигуры по координатам
- Расстояние между точкой и прямой
- Действия с векторами
Количество знаков дробной части
Координаты точки 1
X
Y
Координаты точки 2
X
Y
Координаты точки 3
X
Y
Примечание: Вводить точки необходимо с крайней левой, относительно центра координат по часовой стрелке.
Если фигура с пересекающимися линиями, то последовательно по точкам «движения» линии.
|
KOLIS331 0 / 0 / 0 Регистрация: 12.02.2017 Сообщений: 3 |
||||
|
1 |
||||
Нахождение площади прямоугольника по его вершинам12.02.2017, 17:34. Показов 5490. Ответов 5 Метки нет (Все метки)
Здравствуйте,
0 |
|
Почетный модератор 64287 / 47586 / 32739 Регистрация: 18.05.2008 Сообщений: 115,182 |
|
|
12.02.2017, 17:48 |
2 |
|
площадь прямоугольника по его вершинам, Каким вершинам, как они расположены относительно осей координат? Напишите точное и полное условие задачи.
0 |
|
0 / 0 / 0 Регистрация: 12.02.2017 Сообщений: 3 |
|
|
12.02.2017, 18:13 [ТС] |
3 |
|
Задача: прямоугольник задан координатами своих вершин. Найти его площадь.
0 |
|
Puporev Почетный модератор 64287 / 47586 / 32739 Регистрация: 18.05.2008 Сообщений: 115,182 |
||||
|
12.02.2017, 18:32 |
4 |
|||
|
РешениеЕсли вводятся произвольные координаты вершин в произвольном порядке, то так.
2 |
|
0 / 0 / 0 Регистрация: 12.02.2017 Сообщений: 3 |
|
|
12.02.2017, 18:40 [ТС] |
5 |
|
Спасибо большое воспользуюсь Вашим советом, но к сожелению мы этого не проходили ещё=(
0 |
|
Почетный модератор 64287 / 47586 / 32739 Регистрация: 18.05.2008 Сообщений: 115,182 |
|
|
12.02.2017, 18:44 |
6 |
|
К сожалению если стороны прямоугольника не обязательно параллельны сям координат, а вершины вводятся произвольно, а не в порядке обхода, решение будет сложным.
0 |































 Сообщение было отмечено ZX Spectrum-128 как решение
Сообщение было отмечено ZX Spectrum-128 как решение