Тема нашего урока Задачи на нахождение площади
прямоугольника.
И эта тема у нас сегодня неспроста.
Представляете, у моих соседей Миклуши и Валюши возник спор.
Они сделали две закладки в подарок своей сестре и сейчас спорят.
Миклуша доказывает, что его закладка лучше, потому что больше. А Валюша кричит,
что его закладка больше, поэтому и лучше.
Ну, давайте им поможем. Постараемся их примерить, но для этого мы
должны узнать, чья закладка больше. А для этого нам надо научиться находить
площадь прямоугольника.
Давайте внимательнее рассмотрим закладки.
Обратите внимание, они обе имеют форму прямоугольника. И
нам надо найти площади этих прямоугольников. А что такое площадь? Площадь – это поверхность какой-либо плоской фигуры.
Чтобы найти площадь
какой-нибудь фигуры, нужно выбрать единицу измерения площади. За
единицу измерения площади берут квадрат. Если фигура небольшая,
то у этого квадрата стороны по 1 см, и такой квадрат называется один квадратный
сантиметр.
Если фигуры больше, то за
единицу измерения можно взять 1 квадратный дециметр, т.е. квадрат
со стороной 1 дм, или 1 квадратный метр. Но он такой большой, что
на нашем рисунке просто не поместится.
Но нам надо измерить площади закладок, а для этого нам конечно в
качестве единицы измерения необходимы квадратные сантиметры.
Возникает вопрос, так как найти площадь прямоугольника?
А вот послушайте:
Как измерить площадь?
Нет задачи проще!
Поглядите-ка сюда
Стали мерки в два ряда,
Будто бы солдатики –
Ровные квадратики.
Чтобы площадь нам узнать,
Нужно их … пересчитать!
Раз, два, три, четыре….ммммммм 12. Площадь первой закладки 12
квадратных сантиметров.
А удобно ли каждый раз укладывать такие квадраты? А если нам
надо найти площадь стадиона или сада. Мы же не будем укладывать квадраты. А
если бы начали укладывать, представляете, сколько бы их понадобилось?
Обратите внимания, у нас получились ровные ряды квадратов, значит
в каждом ряду квадратов поровну. Сколько рядов с квадратами получилось?
Три. Сколько квадратов в каждом ряду? Четыре. Как узнать, сколько всего
квадратов?
4 · 3 = 12 квадратов.
А если считать не ряды, а столбики. В нашем прямоугольнике 4
столбика и в каждом по три квадрата. Значит можно считать по-другому:
3 · 4 = 12 квадратов
Мы можем считать количество столбиков или количество
горизонтальных рядов, ответ от этого не меняется.
Так как вы думает можно ли найти площадь прямоугольника, не
застилая его квадратами? Ну конечно, можно.
Подумайте, что обозначает число 4? Это длина прямоугольника. А что
обозначает 3? Это ширина прямоугольника.
Так как мы находили площадь прямоугольника?
Его
длину умножили на его ширину.
В математике принято площадь фигуры обозначать латинской
буквой S. Если длину
прямоугольника обозначить буквой а, а ширину – буквой b, то можно записать, как найти площадь
прямоугольника условной записью S=a·b.
Т.е. чтобы найти площадь прямоугольника, надо
длину умножить на ширину (или ширину на длину).
Итак, мы выяснили, что площадь закладки Валюши равна 12 квадратным
см.
А какова же площадь закладки Миклуши?
Ну что, будем укладывать квадратики… Ой, а зачем мы это делаем? Мы
же знаем другой способ нахождения площади прямоугольника – длину умножить
на ширину.
2 · 6 = 12 квадратных сантиметров.
Так что, получается, что площади обеих закладок
одинаковые? Да, несмотря на то, что у один прямоугольник длинный и узкий, а
второй короткий и широкий, площади у них одинаковые.
Давайте попробуем решить ещё одну задачу.
Кролику подарили семена моркови и сказали, что их хватит на посев
площади в 60 квадратных метров. И Кролик решил посадить морковку и сделал
прямоугольную грядку длинной 12 м и шириной 7 м. Какова площадь грядки у
Кролика? Хватит ли ему семян для этой грядки?
Мы уже знаем, чтобы найти площадь прямоугольника
необходимо его длину умножить на ширину.
Длина грядки 12 метров, ширина 7 метров. Значит, мы:
12 · 7 = 84 квадратных метра.
Ответ: площадь грядки у Кролика 84 квадратных метра.
Увы не хватит Кролику семян для этой грядки – надо срочно бежать в
магазин, докупать. А пока Кролик бегает, мы ещё раз повторим с вами, как
находить площадь прямоугольника.
Чтобы найти площадь прямоугольника, надо умножить длину на
ширину.
Я надеюсь, что вы запомнили, как найти площадь прямоугольника и
без труда сможете её находить.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
2
В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны Найдите площадь прямоугольника, деленную на
3
Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
4
Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
Источник: Диагностическая работа 01.10.2013 Вариант МА90106
5
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
Пройти тестирование по этим заданиям
Задачи на нахождение площади и периметра.
1. Стороны прямоугольника равны 4см и 5см. Найдите площадь и периметр данного прямоугольника.
2. Длина прямоугольника 3дм, ширина равна 2дм. Чему равны площадь и периметр этого прямоугольника?
3. Найдите площадь и периметр квадрата со стороной 6см.
4. Длина прямоугольника 8см, а ширина в 2 раза короче. Чему равна площадь данного прямоугольника?
5. Ширина прямоугольника 5см, а длина в 2 раза длиннее. Найдите площадь и периметр данного прямоугольника?
6. Ширина прямоугольника 4см, длина равна асм. Найдите площадь данного прямоугольника.
7. Площадь прямоугольника 42см², ширина его равна 6см. Чему равна длина прямоугольника?
8. Периметр прямоугольника 20см, ширина его равна 4см. Найдите площадь этого прямоугольника.
9. Периметр квадрата 20см. Найдите площадь этого квадрата.
10. Периметр квадрата 24дм. Какова будет площадь этого квадрата, если его сторону увеличить на 2 дм?
11. Площадь прямоугольника 36см², длина этого прямоугольника 9см. Чему будет равна площадь прямоугольника если длину уменьшить на 2см.
12. Длина клумбы прямоугольной формы 10м, ширина в 2 раза меньше. Найдите площадь клумбы.
13.Часть участка прямоугольной формы площадью 60м² засажена картофелем, другая часть квадратной формы отведена под лук. Длина участка отведенного под лук 4 метра. Чему равна площадь участка занятая картофелем?
14. Четвёртая часть участка длиной 10м, шириной 8 метров, отведена под землянику, а остальная часть — под цветник. Какая площадь занята цветником?
15. Под цветы отведено 2 клумбы. Длина прямоугольной клумбы 10м, ширина 5 метров. Сторона квадратной клумбы 6 метров. Площадь какой клумбы больше и на сколько?
16. Ширина участка 6м, а периметр равен 28 метров. Найдите площадь этого участка.
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и

Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
- Главная
- Справочник
- Как найти площадь прямоугольника
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь прямоугольника
Содержание:
- Формула
- Примеры вычисления площади прямоугольника
Формула
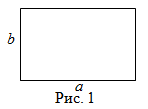
Чтобы найти площадь прямоугольника (рис. 1), надо его длину умножить на ширину, то есть
Прямоугольником называется четырехугольник, у которого все углы равны. Все углы в прямоугольнике прямые, то есть равны $90^{circ}$.
Примеры вычисления площади прямоугольника
Пример
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 см, а вторая, смежная с ней — 5 см.
Решение. Искомая площадь прямоугольника равна произведению двух заданных сторон:
$S=3 cdot 5=15$ (см2)
Ответ. $S=15$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 м, а диагональ — 5 м.
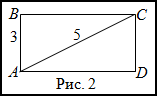
Решение. Сделаем чертеж (рис. 2).
Рассмотрим прямоугольный треугольник $ABC$, из которого по
теореме Пифагора найдем длину катета $BC$ :
$B C=sqrt{A C^{2}-A B^{2}}=sqrt{5^{2}-3^{2}}=sqrt{25-9}=sqrt{16}=4$ (м)
Тогда искомая площадь равна
$S=3 cdot 4=12$ (м2)
Ответ. $S=12$ (м2)
Читать дальше: как найти площадь параллелограмма.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела «Как найти площадь»

Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные