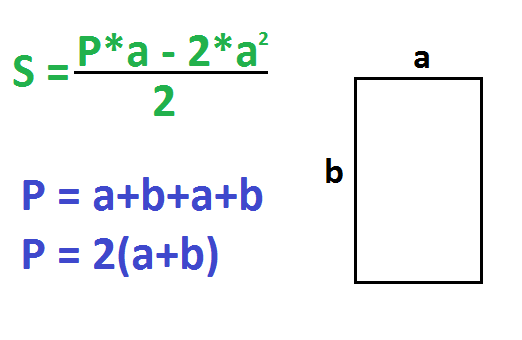Как найти площадь прямоугольника с примером

  • Главная
  • Справочник
  • Как найти площадь прямоугольника

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость

Как найти площадь прямоугольника

Содержание:

  • Формула
  • Примеры вычисления площади прямоугольника

Формула

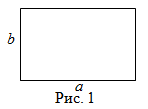
Чтобы найти площадь прямоугольника (рис. 1), надо его длину умножить на ширину, то есть

Прямоугольником называется четырехугольник, у которого все углы равны. Все углы в прямоугольнике прямые, то есть равны $90^{circ}$.

Примеры вычисления площади прямоугольника

Пример

Задание. Найти площадь прямоугольника, если одна его сторона равна 3 см, а вторая, смежная с ней — 5 см.

Решение. Искомая площадь прямоугольника равна произведению двух заданных сторон:

$S=3 cdot 5=15$ (см2)

Ответ. $S=15$ (см2)

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

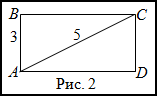
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 м, а диагональ — 5 м.

Решение. Сделаем чертеж (рис. 2).

Рассмотрим прямоугольный треугольник $ABC$, из которого по
теореме Пифагора найдем длину катета $BC$ :

$B C=sqrt{A C^{2}-A B^{2}}=sqrt{5^{2}-3^{2}}=sqrt{25-9}=sqrt{16}=4$ (м)

Тогда искомая площадь равна

$S=3 cdot 4=12$ (м2)

Ответ. $S=12$ (м2)

Читать дальше: как найти площадь параллелограмма.

Статьи по теме

  • Как найти площадь
  • Как найти площадь треугольника
  • Как найти площадь ромба
  • Как найти площадь эллипса
  • Как найти площадь прямоугольного треугольника
  • Все темы раздела «Как найти площадь»

Разделы

  • Формулы сокращенного умножения
  • Формулы по физике
  • Логарифмы
  • Векторы
  • Матрицы
  • Комплексные числа
  • Пределы
  • Производные
  • Интегралы
  • СЛАУ
  • Числа
  • Дроби

Все еще сложно?

Не получается написать работу самому?

Доверь это кандидату наук!

Ищещь ответ на вопрос с которым нужна помощь?

80% ответов приходят в течение 10 минут

250 ответов по вашей теме сегодня

2 специалиста свободны онлайн

Ответы приходят уже через 10 минут

90% ответов положительные

Источник

Выбирайте формулу, ориентируясь на известные величины.

1. Если известны две соседние стороны

Просто перемножьте две стороны прямоугольника.

  • S — искомая площадь прямоугольника;
  • a и b — соседние стороны.

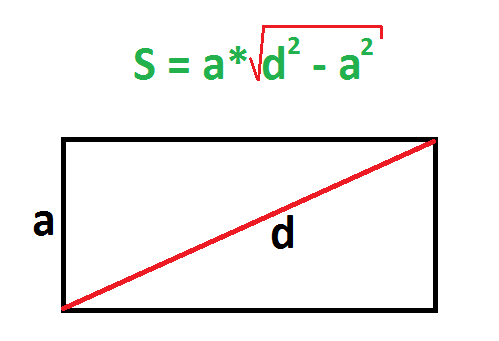
2. Если известны любая сторона и диагональ

Найдите квадраты диагонали и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте длину известной стороны на полученное число.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).

3. Если известны любая сторона и диаметр описанной окружности

Найдите квадраты диаметра и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте известную сторону на полученное число.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • D — диаметр описанной окружности.

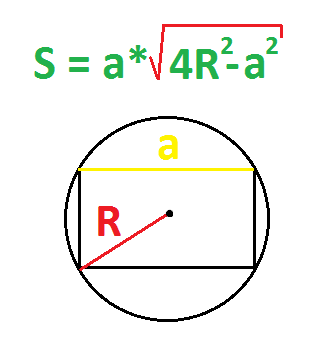
4. Если известны любая сторона и радиус описанной окружности

Найдите квадрат радиуса и умножьте результат на 4.

Отнимите от полученного числа квадрат известной стороны.

Найдите корень из результата и умножьте на него длину известной стороны.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • R — радиус описанной окружности.

5. Если известны любая сторона и периметр

Умножьте периметр на длину известной стороны.

Найдите квадрат известной стороны и умножьте полученное число на 2.

От первого произведения отнимите второе и разделите результат на 2.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • P — периметр прямоугольника (равен сумме всех сторон).

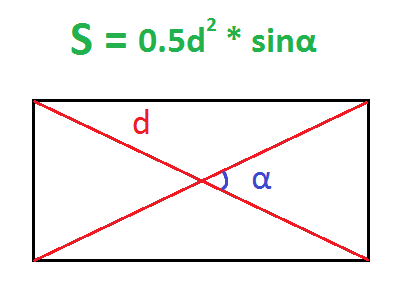
6. Если известны диагональ и угол между диагоналями

Найдите квадрат диагонали.

Разделите полученное число на 2.

Умножьте результат на синус угла между диагоналями.

  • S — искомая площадь прямоугольника;
  • d — любая диагональ прямоугольника;
  • α — любой угол между диагоналями прямоугольника.

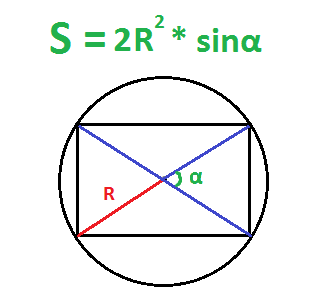
7. Если известны радиус описанной окружности и угол между диагоналями

Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.

Умножьте полученное число на 2, а потом на синус угла между диагоналями.

  • S — искомая площадь прямоугольника;
  • R — радиус описанной окружности;
  • α — любой угол между диагоналями прямоугольника.

Читайте также 🎓❓📐

  • ТЕСТ:​ ​​Умеете ли вы считать в уме?
  • Как легко и быстро считать проценты в уме
  • Как найти площадь любого треугольника
  • ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
  • Как освоить устный счёт школьникам и взрослым
Источник

Рассчитать площадь прямоугольника с подробным решением. Калькулятор находит площадь по формуле через длину и ширину прямоугольника. Основные способы и объяснение формул, по которым вы сможете самостоятельно решить свои задачи.

Онлайн-калькулятор площади прямоугольника

Вначале давайте разберемся с определением. У прямоугольника есть 4 стороны. Каждая сторона равна противоположной и параллельна ей. Здесь важно понимать, что все 4 стороны не могут быть равны, иначе получится квадрат. В прямоугольнике будут 2 одинаковые стороны одной длины и 2 одинаковые другой.

площадь прямоугольника

Все 4 угла, находящиеся внутри прямоугольника, — прямые. То есть каждый угол равен 90°.

прямой угол

Формула площади прямоугольника через его стороны

Чтобы найти площадь SS прямоугольника, нужно перемножить две его стороны: сторону aa умножаем на сторону bb.

S=a⋅b.S = a cdot b.

Пример

У нас есть прямоугольник ABCDABCD. Одна его сторона ABAB равна 55 см, вторая BCBC равна 33 см. Нам нужно найти его площадь SS.

решение примера

Решение:

Чтобы найти площадь SS, нужно умножить сторону ABAB на сторону BCBC и получаем: S=5⋅3S = 5 cdot 3.

Ответ: S=15S = 15 см2.

Формула площади прямоугольника через диагонали

Площадь прямоугольника можно также рассчитать, зная длину диагоналей и острый угол между ними:

S=12d2sin⁡α.S = frac {1}{2}d^2 sin alpha.

Помним, длины диагоналей в прямоугольнике равны и при пересечении делятся пополам.

Пример

Дан прямоугольник ABCDABCD. Его диагональ ACAC равна 88 см, а острый угол между диагоналями 30°30°. Найдите площадь фигуры.

решение примера 2

Используем приведенную выше формулу и получаем:
S=12⋅82⋅sin⁡30∘=12⋅64⋅12=644=16S = frac{1}{2} cdot 8^2 cdot sin 30^{circ} = frac{1}{2} cdot 64 cdot frac{1}{2} = frac{64}{4} = 16

Ответ: S=16S = 16 см2.

Не знаете, как решить задачу по геометрии онлайн? Оформите заказ на Студворк!

Тест по теме «Площадь прямоугольника»

Источник

Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.

11 504

Как найти площадь прямоугольника – 9 формул с примерами

Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.

По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

  1. Найти квадрат диагонали, то есть умножить ее на саму себя.
  2. Найти квадрат известной стороны.
  3. Из квадрата диагонали вычесть квадрат стороны.
  4. Найти квадратный корень получившейся разности.
  5. Умножить его на известную сторону.

Ищем площадь по диагонали и стороне

Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

  1. Квадрат стороны = 3*3 = 9 см.
  2. Квадрат диагонали = 5*5 = 25 см.
  3. Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
  4. Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
  5. Умножаю корень разности на известную сторону: 16*9 = 144 см.

Ответ: 144 см.

Обратите внимание

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

По стороне и диаметру описанной окружности

Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

Действия:

  1. Найдите квадрат диаметра – умножьте диаметр на диаметр.
  2. Найдите квадрат известной стороны.
  3. Отнимите от квадрата диаметра квадрат стороны.
  4. Найдите квадратный корень разности.
  5. Умножьте квадратный корень на известную сторону.

По одной стороне и диаметру окружности

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

  1. Квадрат диаметра: 10*10 = 100 см.
  2. Квадрат стороны: 8*8 = 64 см.
  3. Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
  4. Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
  5. Умножаю сторону на корень из разности: 8*6 = 48 см.

Ответ: 48 см.

Лайфхак

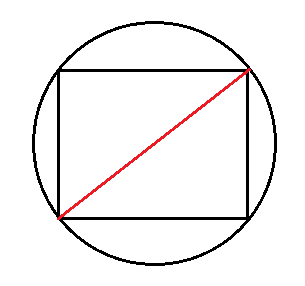
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

Диагональ равна диаметру

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

Как найти площадь треугольника – все способы

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

Другой способ:

  1. Найти квадрат радиуса (умножьте радиус на радиус).
  2. Умножить квадрат радиуса на 4.
  3. Найти квадрат известной стороны.
  4. Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
  5. Найти квадратный корень разности.
  6. Умножить корень на известную сторону.

Площадь по стороне и радиусу

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

  1. Квадрат радиуса: 5*5=25 см.
  2. Четыре квадрата радиуса: 4*25 = 100 см.
  3. Квадрат стороны: 6*6 = 36 см.
  4. Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
  5. Нахожу квадратный корень разности. Корень из 64 равен 8 см.
  6. Умножаю корень на сторону: 8*6 = 48 см.

Ответ: 48 см.

Помните

Радиус = половине диаметра.

Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

По стороне и периметру – 1 способ

Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

Пример. Периметр прямоугольника равен 14 см, а одна из  сторон равна 3 см. Найдите площадь.

  1. Нахожу вторую сторону прямоугольника:
    1. P=2(a+b).
    2. P=2a+2b.
    3. 14= 2*3+2b.
    4. 14 = 6+2b.
    5. 2b = 14-6 = 8.
    6. b = 8/2.
    7. b = 4.
  2. Нахожу площадь по основной формуле. S = 3*4 = 12 см.

Ответ: 12 см.

По стороне и периметру – 2 способ

Действия такие:

  1. Умножьте периметр на сторону.
  2. Найдите квадрат стороны.
  3. Умножьте квадрат стороны на 2.
  4. Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
  5. Поделите на 2.

Как найти площадь, если известны периметр и сторона

Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

  1. Умножаю периметр на сторону: 8*28 = 224 см.
  2. Нахожу квадрат стороны: 8*8 = 64 см.
  3. Умножаю квадрат стороны на два: 64*2 = 84 см.
  4. Отнимаю из первого третье: 224-84 = 140 см.
  5. Делю разность на два: 140/2 = 70 см.

Ответ: 70 см.

По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

Действия:

  1. Найти квадрат диагонали (умножить диагональ на саму себя).
  2. Найти половину этого квадрата – умножить его на 0,5.
  3. Найти синус угла между диагоналями.
  4. Умножить половину квадрата диагонали на синус угла между диагоналями.

Ищем площадь по диагонали и углу

Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

  1. Квадрат диагонали: 10*10 = 100 см.
  2. Половина этого квадрата: 0,5*100 = 50 см.
  3. Синус угла между диагоналями: sin 30 градусов = 0,5.
  4. Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.

Ответ: 25 см.

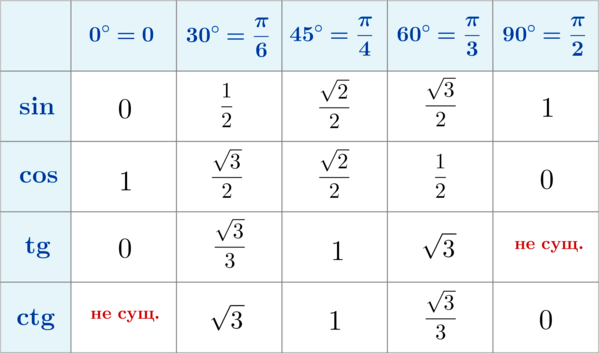
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

Основные значения из тригонометрии

По радиусу описанной окружности и углу между диагоналями – первый способ

Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.

  1. Находим длину диагонали: 6*2 =12 см.
  2. Квадрат диагонали равен 144 см.
  3. Половина квадрата: 72 см.
  4. Синус 30 градусов равен 0,5.
  5. Умножаем половину квадрата на синус: 72*0,5 = 36 см.

Ответ: 36 см.

По радиусу описанной окружности и углу между диагоналями – второй способ

Действия:

  1. Найти квадрат радиуса (умножить радиус на радиус).
  2. Умножить квадрат радиуса на два.
  3. Найти синус угла между диагоналями.
  4. Умножить синус угла на два радиуса в квадрате.

Ищем площадь по радиусу и углу между диагоналями

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.

  1. Квадрат радиуса: 6*6 = 36.
  2. Два радиуса в квадрате: 36*2 = 72.
  3. Синус 30 градусов равен 0,5.
  4. Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.

Ответ: 36 см.

Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.

( 1 оценка, среднее 5 из 5 )

Оцените статью

ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА

Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети

ПОДПИСАТЬСЯ

Источник


Download Article


Download Article

A rectangle is a quadrilateral[1]
 with two sides of equal length and two sides of equal width that contains four right angles. To find the area of a rectangle, all you have to do is multiply its length with its width. If you want to know how to find the area of a rectangle, just follow these easy steps.

  1. Image titled Calculate the Area of a Rectangle Step 1

    1

    Understand the rectangle. The rectangle is a quadrilateral, which means it has four sides.[2]
     Its opposite sides are equal in length, so the sides along its length are equal, and the sides along its width are equal as well. If one side of the rectangle is 10, for example, then the opposite side’s length will also be 10.

    • Also, every square is a rectangle, but not all rectangles are squares. So treat squares like rectangles in terms of finding its area.

  2. Image titled Calculate the Area of a Rectangle Step 2

    2

    Learn the equation for finding the area of a rectangle. The equation for finding the area of a rectangle is simply A = L * W.[3]
     This means that the area is equal to the length of the rectangle times its width.

    3. Advertisement

  1. Image titled Calculate the Area of a Rectangle Step 3

    1

    Find the length of the rectangle. In most cases, you will be given the length, but if not, you can find it using a ruler.[4]
    [5]

    • Note that the double hash marks on the long sides of the rectangle mean that the lengths of the two sides are the same.

  2. Image titled Calculate the Area of a Rectangle Step 4

    2

    Find the width of the rectangle. Use the same methods to find it.[6]

    • Note that the single hash marks on the wide sides of the rectangle mean that the two widths have equal length.

  3. Image titled Calculate the Area of a Rectangle Step 5

    3

    Write the length and width next to each other. In this example, the length is 5 cm and the width is 4 cm.

  4. Image titled Calculate the Area of a Rectangle Step 6

    4

    Multiply the length times the width. Your length is 5 cm and your width is 4 cm, so you should plug them into the equation A = L * W to find the area.[7]

    • A = 4 cm * 5 cm
    • A = 20 cm^2

  5. Image titled Calculate the Area of a Rectangle Step 7

    5

    State your answer in square units. Your final answer is 20 cm^2, which means «twenty centimeters squared.»[8]

    • You can write your final answer in one of two ways: either 20 cm.sq. or 20 cm^2.

    6. Advertisement

  1. Image titled Calculate the Area of a Rectangle Step 8

    1

    Understand the Pythagorean theorem. The Pythagorean theorem is a formula for finding the third side of a right triangle if you know the value of two of the sides. You can use it to find the hypotenuse of a triangle, which is its longest side, or its length or width, which meet at a right angle.[9]

    • Since a rectangle is comprised of four right angles, the diagonal that cuts through the shape will create a right triangle, so you can apply the Pythagorean theorem.
    • The theorem is: a^2 + b^2 = c^2, where a and b are sides of the triangle and c is the hypotenuse, or longest side.[10]

  2. Image titled Calculate the Area of a Rectangle Step 9

    2

    Use the Pythagorean theorem to solve for the other side of the triangle. Let’s say that you have a rectangle with a side of 6 cm and a diagonal of 10 cm. Use 6 cm for one side, use b for the other side, and take 10 cm as your hypotenuse. Now just substitute your known quantities into the Pythagorean theorem and solve. Here’s how to do it:[11]

    • Ex: 6^2 + b^2 = 10^2
    • 36 + b^2 = 100
    • b^2 = 100 — 36
    • b^2 = 64
    • square root (b) = square root (64)
    • b = 8
      • The length of the other side of the triangle, which is also the other side of the rectangle, is 8 cm.

  3. Image titled Calculate the Area of a Rectangle Step 10

    3

    Multiply the length times the width. Now that you’ve used the Pythagorean theorem to find the length and width of the rectangle, all you have to do is multiply them.[12]

    • Ex: 6 cm * 8 cm = 48 cm^2

  4. Image titled Calculate the Area of a Rectangle Step 11

    4

    State your answer in square units. Your final answer is 48 cm^2, or 48 cm. sq.

    5. Advertisement

Calculator, Practice Problems, and Answers

Add New Question

  • Question

    How do I find the area in meters?

    Community Answer

    You cannot find an area in meters, because area is expressed in square meters.
    If the values of your rectangle sides are not in meters, then you must first convert those units to meters, and then multiply the converted values to get the area in square meters.

  • Question

    If the problem says length is 105 breadth is 81 and other said of length is 103 and breadth is 53, how do I find the area of the rectangle?

    Community Answer

    A rectangle has 2 sides of equal length and 2 sides of equal width (breadth). By definition, the object in which you are describing is not a rectangle. The object you have is an irregular quadrilateral.

  • Question

    How do I find the area of a rectangle when each side is a different length?

    Community Answer

    It is not a rectangle if each side is a different length. It is either an irregular shape or a trapezoid. There is no formula for finding the area of an irregular shape. The area of a trapezoid is found by multiplying its height by the average of its bases.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Advertisement

  • All squares are rectangles. However, not all rectangles are squares.

  • If you’re finding area, your answer will always be squared.

Advertisement

About This Article

Article SummaryX

To quickly calculate the area of a rectangle, find the length of the base. Then, multiply the base by the height of the rectangle to get the area. For example, a rectangle with a base of 6 and a height of 9 has an area of 54. Be sure to include the units of the measurements in your answer. If you need to find the area if you only know the area or the length of 1 side and a diagonal, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 594,819 times.

Did this article help you?

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти майнкрафт любят
  • Одна половина лица больше другой как исправить
  • Как исправить провод от наушников
  • Как составить официальное письмо в управляющую компанию
  • Как исправить ошибку gta 5 installation path has not been automatically detected