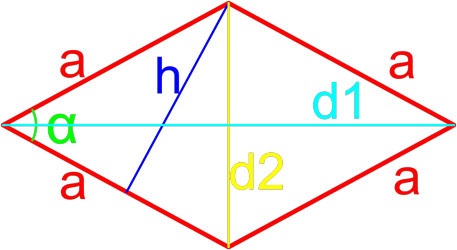
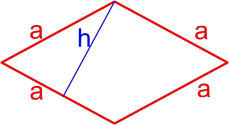
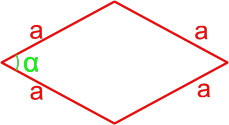
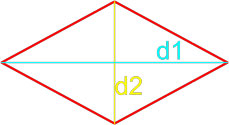
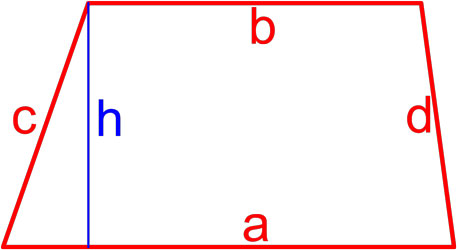
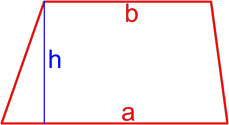
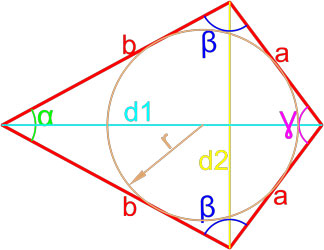
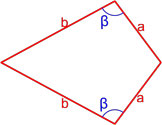
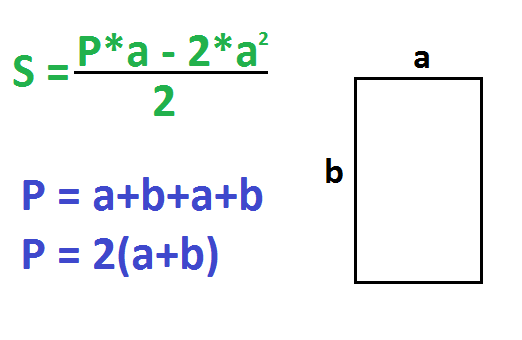Как найти площадь прямоугольника – 9 способов с формулами и примерами
Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
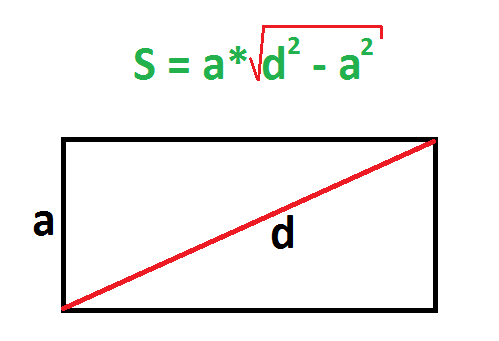
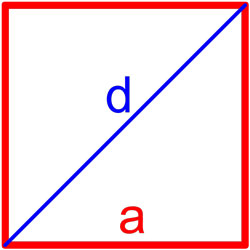
По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
- Найти квадрат диагонали, то есть умножить ее на саму себя.
- Найти квадрат известной стороны.
- Из квадрата диагонали вычесть квадрат стороны.
- Найти квадратный корень получившейся разности.
- Умножить его на известную сторону.
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
- Квадрат стороны = 3*3 = 9 см.
- Квадрат диагонали = 5*5 = 25 см.
- Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
- Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
- Умножаю корень разности на известную сторону: 16*9 = 144 см.
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
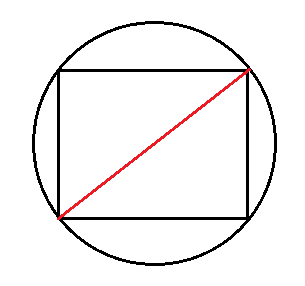
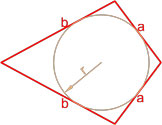
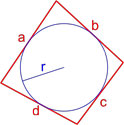
По стороне и диаметру описанной окружности
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
- Найдите квадрат диаметра – умножьте диаметр на диаметр.
- Найдите квадрат известной стороны.
- Отнимите от квадрата диаметра квадрат стороны.
- Найдите квадратный корень разности.
- Умножьте квадратный корень на известную сторону.
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
- Квадрат диаметра: 10*10 = 100 см.
- Квадрат стороны: 8*8 = 64 см.
- Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
- Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
- Умножаю сторону на корень из разности: 8*6 = 48 см.
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
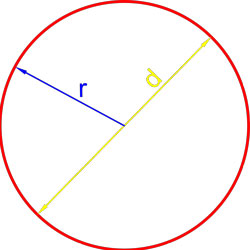
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.
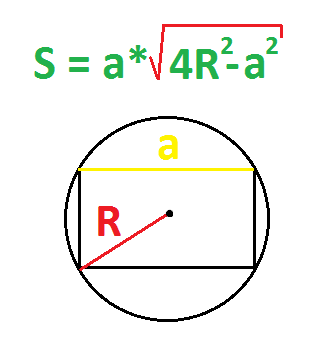
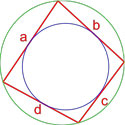
По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
- Найти квадрат радиуса (умножьте радиус на радиус).
- Умножить квадрат радиуса на 4.
- Найти квадрат известной стороны.
- Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
- Найти квадратный корень разности.
- Умножить корень на известную сторону.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
- Квадрат радиуса: 5*5=25 см.
- Четыре квадрата радиуса: 4*25 = 100 см.
- Квадрат стороны: 6*6 = 36 см.
- Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
- Нахожу квадратный корень разности. Корень из 64 равен 8 см.
- Умножаю корень на сторону: 8*6 = 48 см.
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
- Нахожу вторую сторону прямоугольника:
- P=2(a+b).
- P=2a+2b.
- 14= 2*3+2b.
- 14 = 6+2b.
- 2b = 14-6 = 8.
- b = 8/2.
- b = 4.
- Нахожу площадь по основной формуле. S = 3*4 = 12 см.
По стороне и периметру – 2 способ
- Умножьте периметр на сторону.
- Найдите квадрат стороны.
- Умножьте квадрат стороны на 2.
- Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
- Поделите на 2.
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
- Умножаю периметр на сторону: 8*28 = 224 см.
- Нахожу квадрат стороны: 8*8 = 64 см.
- Умножаю квадрат стороны на два: 64*2 = 84 см.
- Отнимаю из первого третье: 224-84 = 140 см.
- Делю разность на два: 140/2 = 70 см.
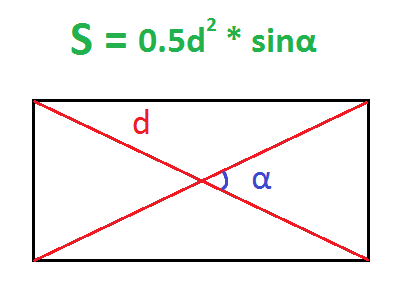
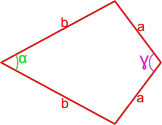
По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
- Найти квадрат диагонали (умножить диагональ на саму себя).
- Найти половину этого квадрата – умножить его на 0,5.
- Найти синус угла между диагоналями.
- Умножить половину квадрата диагонали на синус угла между диагоналями.
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.
- Квадрат диагонали: 10*10 = 100 см.
- Половина этого квадрата: 0,5*100 = 50 см.
- Синус угла между диагоналями: sin 30 градусов = 0,5.
- Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.
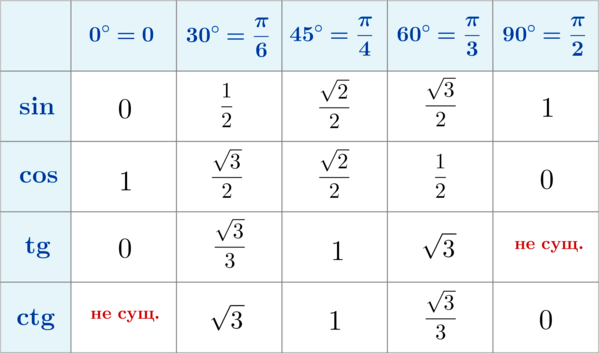
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
- Находим длину диагонали: 6*2 =12 см.
- Квадрат диагонали равен 144 см.
- Половина квадрата: 72 см.
- Синус 30 градусов равен 0,5.
- Умножаем половину квадрата на синус: 72*0,5 = 36 см.
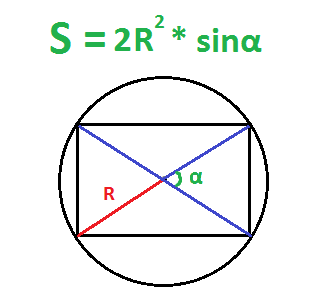
По радиусу описанной окружности и углу между диагоналями – второй способ
- Найти квадрат радиуса (умножить радиус на радиус).
- Умножить квадрат радиуса на два.
- Найти синус угла между диагоналями.
- Умножить синус угла на два радиуса в квадрате.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
- Квадрат радиуса: 6*6 = 36.
- Два радиуса в квадрате: 36*2 = 72.
- Синус 30 градусов равен 0,5.
- Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
Журнал Педагог
Автор: Беспалова Любовь Иннокентьевна
Должность: учитель математики
Учебное заведение: МОУ «Ульканская общеобразовательная школа №2»
Населённый пункт: п.Улькан
Наименование материала: методическая разработка
Тема: Площадь прямоугольника, вписанного в окружность
Раздел: среднее образование
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа №2»
Автор: Беспалова Любовь Иннокентьевна
Тема методической разработки: «Площадь прямоугольника,
вписанного в окружность»,интегрированный урок геометрии
и информатики
2013 П.УЛЬКАН
Тема урока
: Площадь прямоугольника, вписанного в окружность.
Цели урока
: расширить знания учащихся по теме «Площадь прямоугольника»; закрепить умения учащихся работать в текстовом редакторе MS Word
Задачи урока
: Образовательные: вывести формулу площади прямоугольника, вписанного в окружность, через радиус окружности и угол между диагональю прямоугольника и одной из его сторон и исследовать ее; Используя информационные технологии закрепить теоретические знания, полученные на уроках информатики по теме: «Текстовый редактор MS Word» при выполнении исследований; Развивающие: развитие логического мышления учащихся, навыков набора текста и работы с несколькими документами одновременно; Воспитательные: воспитание чувства коллективизма, взаимопомощи, взаимоуважения. Точности, аккуратности и внимания в процессе выполнения работы; Содействовать рациональной организации труда школьников.
Оборудование урока
: OC Microsoft Windos XP, MS Word, проектор, экран, циркули, линейки, плакат « Ги п от е з а –научное предположение, выдвигаемое для объяснения какого – либо явления и требующее проверки на опыте и теоретического обоснования для того, чтобы стать достоверной научной теорией; вообще – предположение, требующее подтверждения» , карточки для выполнения практической работы и для более подготовленных учащихся, таблица «Площади» Площадь прямоугольника a S = ab b Площадь параллелограмма b h S = ah, S = ab sin a Площадь треугольника b c S = ah, S = ab sin , h а S =
a p = Площадь трапеции h S = b Площадь ромба S = d 1 d 2 Площадь квадрата S = a 2 а Площадь треугольника, вписанного в окружность S = а Площадь треугольника, S = описанного около окружности rr b c а 2 Площадь многоугольника, а 3 описанного около а 1 S = rP
окружности d 1 d 2 dddd d a b R c r r r
O
а 4
Тип урока: урок изучения нового материала.
Вид урока — интегрированный: математика, информатика
Продолжительность урока 90 минут
информатики:
Ребята! Сегодняшний урок необычный: урок информатики мы сегодня проводим совместно с геометрией. П.Л. Чебышев сказал: «Сближение теории с практикой дает самые благотворные результаты, и не одна практика от этого выигрывает, сами науки развиваются под ее влиянием». (Слайд 1)
Учитель математики:
Сообщаются тема и цель урока. (Слайд 2)
II.
Проверка домашнего задания:
1.
Учитель математики
: проверим решение задачи 49 из параграфа 14, (Слайд 3) 2.
Учитель информатики:
На компьютерах изобразите решение домашней задачи и отправьте файл, имя которому ваша фамилия на сервер. Учащиеся работают на компьютерах, на экране правильное решение задачи. Подводятся итоги, учитель математики отвечает на вопросы учащихся. (Слайд 4) a 1 Разделим многоугольник на n треугольников с вершинами в rr a 3 центре окружности. S – площадь многоугольника, равна сумме a 2 площадей треугольников (обозначим их S 1, S 2,………., S n ). S = ah, h = r S = S 1 + S 2 + S 3 +……… + S n = a n a 1 r + a 2 r + a 3 r +……..+ a n r = r(a 1 + a 2 +….+ a n ) = rP
a 4
где Р – периметр многоугольника, r – радиус вписанной окружности
Учитель математики:
Фронтальный опрос: а) На доске начерчен прямоугольный треугольник, обозначены его катеты и гипотенуза. Сформулировать и записать теорему Пифагора. б) Дать определение синуса угла в прямоугольном треугольнике. Записать его на доске. r r
O
в) Дать определение косинуса угла в прямоугольном треугольнике. Записать его на доске. г) Записать формулу площади прямоугольника. д) Записать формулу синуса двойного угла. е) Назовите наибольшее и наименьшее значение синуса угла. ж) Где находится точка пересечения диагоналей прямоугольника, вписанного в окружность?
III Изучение нового материала:
1.
Учитель
математики:
Мы с вами научились находить площади прямоугольника, параллелограмма, треугольников, применяя различные формулы, трапеции, ромба, квадрата, треугольников, вписанных в окружность, и треугольников, описанных около окружности, доказали, что площадь многоугольника, описанного около окружности, равна половине произведения периметра многоугольника на радиус вписанной окружности. (Обратить внимание учащихся на таблицу «Площади») 2. А сегодня на уроке мы попробуем с помощью микроисследования открыть и доказать еще одну формулу для нахождения площади прямоугольника. Учащиеся записывают тему урока: «Площадь прямоугольника, вписанного в окружность». Для этого требуется решить задачу: (слайд 5) Чтобы облегчить решение задачи, давайте мы с вами выполним практическую работу. Только радиус круга возьмем не 50 см, а 5 см. (Обратить внимание учащихся на плакат с разъяснением слова «Гипотеза», на местоположение точки пересечения диагоналей прямоугольника, вписанного в окружность) 3. Практическая работа.
Учитель информатики:
работу выполнить на компьютерах: (каждому ученику дается карточка) Выполни практическую работу. 1. В окружность радиуса 5 см впишите прямоугольник с основанием a см. Величина a принимает значения, указанные в таблице. Заполни таблицу. 2. Назовите наибольшее значение из получившихся площадей. 3. Сформулируйте гипотезу о форме прямоугольника наибольшей площади, вписанного в окружность. 4. Задание для более подготовленных учащихся: a (см) 2 3 4 5 6 7 8 9 b (см) S(см 2 )
Выразить площадь прямоугольника через радиус описанной окружности и угол между стороной прямоугольника и его диагональю. Исследовав эту формулу, ответьте на вопросы: 1. В каком случае площадь прямоугольника будет наибольшей? 2. Какую форму имеет прямоугольник наибольшей площади, вписанный в окружность? 3. Записать формулу площади прямоугольника, имеющего наибольшую площадь. После выполнения практической работы один из учеников выводит результаты исследований на экран в виде таблицы и подтверждает правильность выдвинутой гипотезы. (Ответ учащихся: гипотеза — из всех прямоугольников, вписанных в окружность, наибольшую площадь имеет квадрат).
Учитель математики:
Требуется привести доказательство гипотезы — их всех прямоугольников, вписанных в окружность, наибольшую площадь имеет квадрат. Это делает один из учеников, который выполнял индивидуальную работу. Предполагаемый ответ ученика: Чтобы это доказать, выводим формулу площади прямоугольника, вписанного в окружность через радиус окружности и угол между диагональю прямоугольника и его стороной. A B Центр окружности лежит в точке пересечения диагоналей прямоугольника. АС = 2R. S ABCD = ab. Из прямоугольного треугольника ADC следует, что = , a = 2R , = , b = 2R , S ABCD = ab = 2R 2R = 4R 2 = D C 2R 2 . a (см) 2 3 4 5 6 7 8 9 b (см) S(см 2 ) а b
Площадь прямоугольника, вписанного в окружность, равна 2R 2 , где R –радиус окружности, — угол между диагональю прямоугольника и его стороной. Наш прямоугольник должен по условию задачи иметь наибольшую площадь. Исследуем эту формулу: S = 2R 2 . 2R 2 – величина для этой окружности постоянна. Наибольшее значение площади зависит от , наибольшее значение синуса угла равно 1, тогда = 1, = , = , т.е. угол между диагональю и стороной прямоугольника равен , откуда следует, что прямоугольник наибольшей площади, вписанный в окружность, является квадратом. Тогда площадь квадрата (прямоугольника, имеющего наибольшую площадь) равна S = 2R 2 .
Учитель математики:
1. Получили новые формулы для вычисления площади прямоугольника: S = 2R 2 — площадь прямоугольника, вписанного в окружность, где R – радиус вписанной окружности, — угол между диагональю (диаметром окружности) прямоугольника и стороной прямоугольника. S = 2R 2 – площадь квадрата, вписанного в окружность (прямоугольника, вписанного в окружность наибольшей площади) 2. Задание классу: по полученной формуле найти площадь прямоугольника, имеющего наибольшую площадь, вписанного в окружность. R = 5 см (50 см 2 ) 3. Сравнить значение площади, вычисленной по полученной формуле со значением площади, полученной в результате исследований. 4. Вопрос классу: подтвердилась ли выдвинутая гипотеза: их всех прямоугольников, вписанных в окружность, наибольшую площадь имеет квадрат? 5. Решить задачу: (слайд 5) Из круглого листа жести радиуса 50 см требуется вырезать прямоугольник наибольшей площади. Найти значение этой площади. Учащиеся должны ответить на вопросы: а) Как из круглого листа жести вырезать прямоугольник наибольшей площади? (предполагаемый ответ: на круглом листе жести провести два взаимно перпендикулярных диаметра, концы диаметра последовательно соединить отрезками, получим прямоугольник (квадрат), который имеет наибольшую площадь). (Слайд 6) б) Чему равно значение этой площади? (5000 см 2 )
IV Первичное закрепление материала
1. Решение задач: (выполняется в тетради) — а) Вывести формулу площади квадрата через его диагональ двумя способами. (Слайд 7)
A B 1 способ (Слайд 
=
45 , a = d sin = d; a S = 2 = 2 , S = 2 .
2 способ (Слайд 9)
C D Квадрат – это ромб, диагонали ромба равны (d 1 = d 2 ).
Формула площади ромба: S = d 1 d 2 , площадь квадрата: S = 2 . б) Боковая сторона равнобедренного треугольника равна 18 см. Найти наибольшую возможную площадь этого треугольника. (Слайд 10) (Слайд 11) A K Треугольник АВС – равнобедренный, АМ – высота, Проведем АК МС, КС АМ, площадь
18
прямоугольника АКСМ равна площади
треугольника АВС ( АМВ = СКА (равенство
B M C прямоугольных треугольников по двум катетам: АМ = КС, ВМ = МС, МС = АК, тогда АК = МС)). Прямоугольник АКСМ будет иметь наибольшую площадь, если он будет являться квадратом. S кв = 2 , S АКСМ = 18 2 = 324:2 = 162 (см 2 ). Так как площадь прямоугольника АКСМ равна площади треугольника АВС, то наибольшая площадь треугольника АВС равна 162 см 2 .
V Задание на дом:
(Слайд 12) 1. Вывод формулы площади прямоугольника, вписанного в окружность, через диагональ прямоугольника и угол между диагональю прямоугольника и его стороной; 2. Задание по карточке: (карточка выдается каждому учащемуся) d
Домашнее задание
1. Задача: Нужно огородить участок прямоугольной формы забором длиной 200м. Каковы должны быть размеры этого участка, чтобы его площадь была наибольшей? 2. Переформулировать задачу, взяв за периметр прямоугольника 20 см. 3. Заполнить таблицу: a (см) 1 2 3 4 5 6 7 8 9 b (см) S (cм 2 ) 4. Запишите наибольшее значение из получившихся площадей. 5. Сформулируйте гипотезу о форме прямоугольника заданного периметра, имеющего наибольшую площадь. 6. Решить данную задачу. 7. Выполни задание в среде MS Word. 3. (
Учитель математики)
(Слайд 13)
Тест
1.
Площадь ромба с диагоналями 10 см и 20 см равна: а) 200 см 2 б) 300 см 2 в) 400 см 2 г) 100 см 2 2. Площадь квадрата со стороной 5 см равна: а) 20 см 2 б) 10 см 2 в) 25 см 2 г) 15 см 2 3. Боковая сторона равнобедренного треугольника равна 24 см. При каком значении высоты площадь треугольника будет наибольшей? Проверяется результат, анализируется решение задачи. а) 12 см; б) 12 см; в) 12 см; г) 8 см.
VI Итог урока
1.
Вопросы классу: (
Учитель математики)
а) формула площади прямоугольника, вписанного в окружность, через радиус окружности и угол между диагональю прямоугольника и его стороной; какую форму имеет прямоугольник, вписанный в окружность, наибольшей площади? б) формула площади квадрата через его диагональ.
Учитель информатики
: -Какие функции необходимо использовать при вставке фигур в документ? — Какими способами можно задать таблицу в MS WORD? 2. Выставление оценок по математике и информатике.
Учитель математики:
Закончить сегодняшний урок хочется словами великого Леонардо до Винчи: « Железо ржавеет, не находя себе применения, стоячая вода гниет или на холоде замерзает, а ум человека, не находя себе применения, чахнет». Мы хотим, чтобы ваш ум никогда не зачах. (Слайд 14)
Литература
1. Современный словарь иностранных слов. Москва «Русский язык», 1993 г. 2. А.В.Погорелов «Геометрия 7 – 9», учебник, «Просвещение» 2005 г. 3. Т.И.Купорова «Геометрия 9 класс, поурочные планы по учебнику А.В.Погорелова», Волгоград «Учитель», 2003 г. 4. И.М.Шапиро «Использование задач с практическим содержанием в преподавании математики», Москва «Просвещение», 1990 г. 5. А.Г.Мордкович «Алгебра и начала математического анализа 10 – 11, часть 2, задачник», Москва «Просвещение», 2009 г. 6. А.А. Кузнецов, Н.В. Апатова «Основы информатики», «Просвещение», 2008 г 7. А.А.Журин, И.П.Журина «Word 7.0 для школьников» «Дрофа», 2007 г.
Формулы площадей фигур
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.
Формула площади треугольника по трем сторонам
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .
S = p p — a p — b p — c ,
где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1 2 a · b · sin γ ,
где a, b — стороны треугольника,
γ — угол между сторонами a и b .
Формула площади треугольника по трем сторонам и радиусу описанной окружности
a, b, c — стороны треугольника,
R — радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2
Формулы площади квадрата
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
где S — площадь квадрата,
a — длина стороны квадрата.
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
где S — площадь квадрата,
d — длина диагонали квадрата.
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон.
где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.
Формулы площади параллелограмма
Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.
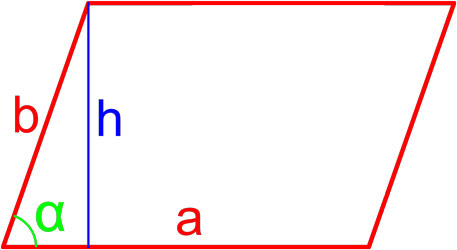
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α — угол между сторонами параллелограмма.
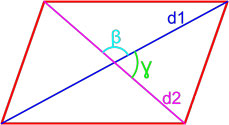
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
S = d1 · d2 · sin β 2 = d1 · d2 · sin γ 2 ,
где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β , γ — угол между диагоналями параллелограмма.
Формулы площади ромба
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
где S — площадь ромба,
d1, d2 — длины диагоналей ромба.
Формулы площади трапеции
Трапеция — это четырёхугольник, у которого две ( a, b ) стороны параллельны (основания), а две другие ( c, d ) стороны не параллельны (боковые стороны).
Формула Герона для трапеции
где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d 2 — полупериметр трапеции.
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы её оснований на высоту.
где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.
Формулы площади дельтоида
Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.
Формула площади дельтоида по двум неравным сторонам и углу между ними
Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.
Формула площади дельтоида по равным сторонам и углу между ними
Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.
S = a 2 sin γ + b 2 sin α 2 ,
где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b ,
γ — угол между равными сторонами a .
Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности
Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.
где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.
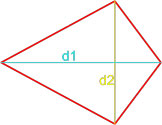
Формула площади дельтоида по двум диагоналям
Площадь дельтоида равна половине произведения длин двух диагоналей.
где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.
Формулы площади произвольного выпуклого четырехугольника
Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними
Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.
S = d1 · d2 · sin γ 2 ,
где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.
Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника,
θ = α + β 2 — полусумма двух противоположных углов четырехугольника.
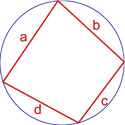
Формула площади вписанного четырехугольника (формула Брахмагупты)
Если вокруг четырехугольника можно описать окружность, то его площадь равна
S = p — a p — b p — c p — d ,
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника.
Формула площади четырехугольника с вписанной окружностью
Если в четырехугольник можно вписать окружность, то его площадь равна:
где S — площадь четырехугольника,
r — радиус вписанной окружности,
p = a + b + c + d 2 — полупериметр четырехугольника.
Формула площади четырехугольника с вписанной и описанной окружностями
Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.
Формулы площади круга
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.
где S — площадь круга,
r — радиус круга.
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.
где S — площадь круга,
d — диаметр круга.
Площадь сегмента круга
Площадь кругового сегмента через угол в градусах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.
Площадь кругового сегмента через угол в радианах.
где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.
Формула площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.
http://zhurnalpedagog.ru/servisy/publik/publ?id=3392
http://urokmatematiki.ru/reference-information/formuly-po-geometrii/formuly-ploshchadey-figur.php

площадь круга равна Q. Найти площадь вписанного в него прямоугольника, отношение длин сторон которого m:n
Светило науки — 3328 ответов — 40600 раз оказано помощи
Прямоугольник со сторонами а и b, по условию а:b=m:n, a=mb/n. Диагональ прямоугольника является диаметром описанной окружности, значит по т.Пифагора d²=a²+b²=b²(m²/n²+1). Площадь круга Q=πR²=πd²/4, откуда d²=4Q/π. Подставляем: 4Q/π=b²(m²/n²+1), откуда b²=4Q/π(m²/n²+1). Т.к. площадь прямоугольника S=a*b=mb/n*b=mb²/n=4Qm/nπ(m²/n²+1)=4Qmn/π(m²+n²)
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given two rectangles, X with a ratio of length to width a:b and Y with a ratio of length to width c:d respectively. Both the rectangles can be resized as long as the ratio of sides remains the same. The task is to place the second rectangle inside the first rectangle such that at least 1 side is equal and that side overlaps of both the rectangles and find the ratio of (space occupied by a 2nd rectangle) : (space occupied by the first rectangle).
Examples:
Input: a = 1, b = 1, c = 3, d = 2 Output: 2:3 The dimensions can be 3X3 and 3X2. Input: a = 4, b = 3, c = 2, d = 2 Output: 3:4 The dimensions can be 4X3 and 3X3
Approach: If we make one of the sides of rectangles equal then the required ratio would be the ratio of the other side.
Consider 2 cases:
- a*d < b*c : We should make a and c equal.
- b*c < a*d : We should make b and d equal.
Since multiplying both sides of a ratio does not change its value. First try to make a and c equal, it can be made equal to their lcm by multiplying (a:b) with lcm/a and (c:d) with lcm/c. After multiplication, the ratio of (b:d) will be the required answer. This ratio can be reduced by dividing b and d with gcd(b, d).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void printRatio(int a, int b, int c, int d)
{
if (b * c > a * d) {
swap(c, d);
swap(a, b);
}
int lcm = (a * c) / __gcd(a, c);
int x = lcm / a;
b *= x;
int y = lcm / c;
d *= y;
int k = __gcd(b, d);
b /= k;
d /= k;
cout << b << ":" << d;
}
int main()
{
int a = 4, b = 3, c = 2, d = 2;
printRatio(a, b, c, d);
return 0;
}
Java
import java.io.*;
class GFG {
static int __gcd(int a, int b)
{
if (a == 0)
return b;
if (b == 0)
return a;
if (a == b)
return a;
if (a > b)
return __gcd(a-b, b);
return __gcd(a, b-a);
}
static void printRatio(int a, int b, int c, int d)
{
if (b * c > a * d) {
int temp = c;
c =d;
d =c;
temp =a;
a =b;
b=temp;
}
int lcm = (a * c) / __gcd(a, c);
int x = lcm / a;
b *= x;
int y = lcm / c;
d *= y;
int k = __gcd(b, d);
b /= k;
d /= k;
System.out.print( b + ":" + d);
}
public static void main (String[] args) {
int a = 4, b = 3, c = 2, d = 2;
printRatio(a, b, c, d);
}
}
Python3
import math
def printRatio(a, b, c, d):
if (b * c > a * d):
swap(c, d)
swap(a, b)
lcm = (a * c) / math.gcd(a, c)
x = lcm / a
b = int(b * x)
y = lcm / c
d = int(d * y)
k = math.gcd(b,d)
b =int(b / k)
d = int(d / k)
print(b,":",d)
if __name__ == '__main__':
a = 4
b = 3
c = 2
d = 2
printRatio(a, b, c, d)
C#
using System;
class GFG {
static int __gcd(int a, int b)
{
if (a == 0)
return b;
if (b == 0)
return a;
if (a == b)
return a;
if (a > b)
return __gcd(a-b, b);
return __gcd(a, b-a);
}
static void printRatio(int a, int b, int c, int d)
{
if (b * c > a * d) {
int temp = c;
c =d;
d =c;
temp =a;
a =b;
b=temp;
}
int lcm = (a * c) / __gcd(a, c);
int x = lcm / a;
b *= x;
int y = lcm / c;
d *= y;
int k = __gcd(b, d);
b /= k;
d /= k;
Console.WriteLine( b + ":" + d);
}
public static void Main () {
int a = 4, b = 3, c = 2, d = 2;
printRatio(a, b, c, d);
}
}
PHP
<?php
function __gcd($a, $b)
{
if ($a == 0)
return $b;
if ($b == 0)
return $a;
if ($a == $b)
return $a;
if ($a > $b)
return __gcd($a - $b, $b);
return __gcd($a, $b - $a);
}
function printRatio($a, $b, $c, $d)
{
if ($b * $c > $a * $d)
{
$temp = $c;
$c = $d;
$d = $c;
$temp = $a;
$a = $b;
$b = $temp;
}
$lcm = ($a * $c) / __gcd($a, $c);
$x = $lcm / $a;
$b *= $x;
$y = $lcm / $c;
$d *= $y;
$k = __gcd($b, $d);
$b /= $k;
$d /= $k;
echo $b . ":" . $d;
}
$a = 4; $b = 3; $c = 2; $d = 2;
printRatio($a, $b, $c, $d);
?>
Javascript
<script>
function __gcd(a, b)
{
if (a == 0)
return b;
if (b == 0)
return a;
if (a == b)
return a;
if (a > b)
return __gcd(a - b,b);
return __gcd(a, b - a);
}
function printRatio(a, b, c, d)
{
if (b * c > a * d)
{
temp = c;
c = d;
d = c;
temp = a;
a = b;
b = temp;
}
let lcm = (a * c) / __gcd(a, c);
let x = lcm / a;
b *= x;
let y = lcm / c;
d *= y;
let k = __gcd(b, d);
b /= k;
d /= k;
document.write(b + ":" + d);
}
let a = 4, b = 3, c = 2, d = 2;
printRatio(a, b, c, d);
</script>
Time complexity: O(log(max(a,c))+log(max(b,d)))
Auxiliary Space: O(log(max(a,c))+log(max(b,d)))
Last Updated :
11 Jul, 2022
Like Article
Save Article

В прямоугольник со сторонами 3 и 4 м вписан другой прямоугольник, стороны которого относятся как 1:3. Найдите площадь вписанного прямоугольника

Светило науки — 7301 ответ — 44626 раз оказано помощи
По теореме Пифагора получаем такие соотношения
[tex]y^2+x^2=z^2
(3-x)^2+(4-y)^2=9z^2
frac{y}{x}=frac{3-x}{4-y}
9y^2+9x^2-((3-x)^2+(4-y)^2)=0
4y-y^2=3x-x^2
8y^2+8x^2+8y+6x-25=0
x^2-y^2=3x-4y
x=frac{9}{8}
y=frac{5}{8}
[/tex]
я уже проверил решение
тогда стороны вписанного прямоугольника
[tex]sqrt{frac{9}{8}^2+frac{5}{8}^2} = sqrt{frac{106}{64}}
3sqrt{frac{106}{64}}
S=sqrt{frac{106}{64}}^2*3=frac{106*3}{64}=4frac{31}{32}[/tex]

Сандер (по-прежнему ленюсь сделать построения на бумаге, настолько уверна в своём «мысленном построении, ну и опираясь на первый рисунок, и на Ваш тоже),
полностью согласна со всеми четырьмя предложениями, сказанным после рисунка, и с их явной очевидностью.
(Исходя из канонического определения прямоугольника можно догадаться, что противоположные стороны его равны по длине и параллельны. Как следствие, треугольники, ограниченные отрезком «С» и «контактными» сторонами большого прямоугольника тождественны. Так же, очевидно (на мой взгляд), что оставшиеся 2 треугольника должны быть подобны маленьким. Еще, на всякий случай: центры окружностей, описанных вокруг каждого из прямоугольников будут совпадать.)
И, конечно: углы, возникающие, если продолжить все стороны прямоугольников в бесконечность — все соответствуют школьному курсу геометрии (fi, и 90-fi, и 180-fi).
Однако , опровергаю эту часть вашего ответа:
заодно поворачиваются перпендикулярные отрезку прямые и… могут выйти в т. ч. и на одну сторону большого прямоугольника.
вот это слово «могут» — я заранее предупредила своими: так, чтобы точки С1 и С2 заскользили по сторонам БоПр, но не вышли за его границы и даже не коснулись вершин БоПр
Т.е. выйти-то — могут, конечно! но для нас я беру только то множество прямоугольников, которые образуются при скольжении С1 и С2 по сторонам БоПр, пока С1 и С2 не вышли за разрешённые им границы.
(когда в след.раз найдётся время на развлечения и дойду до бумаги и до компа (второе труднее) — это м.б.и на следующей неделе — начну с того, что просто впишу попробую вписать два разных маленьких прямоугольника, но с одинаковой длиной одной из сторон, в один большой прямоугольник, и представлю сюда конкретные цифры. Если это не получится, во-первых, очень сильно удивлюсь, во-вторых, буду искать ошибку в своём «мыслительном» способе построения таких простых геометрическихх фигур, и только в третьих — решать эту конкретную задачу)