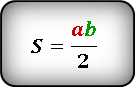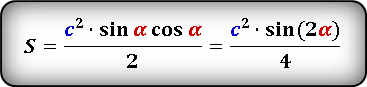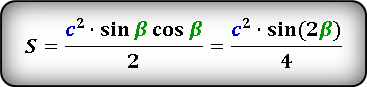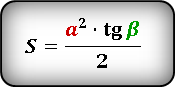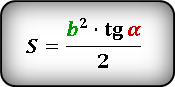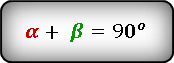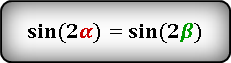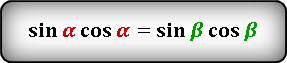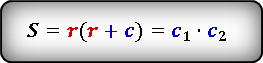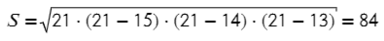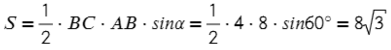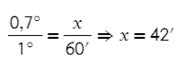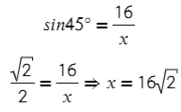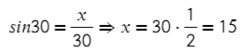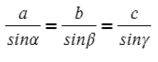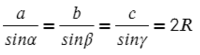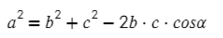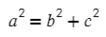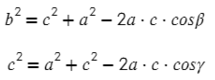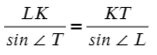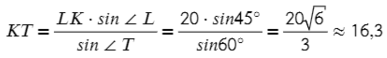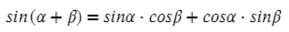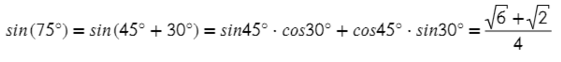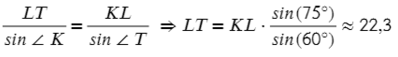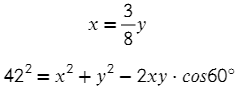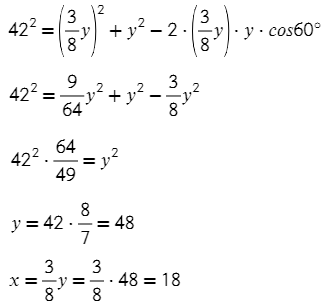Площадь треугольника через углы, формула
Площадь треугольника через две стороны и угол между ними, формула
Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними.
Площадь треугольника через одну сторону и прилежащие к ней углы, формула
Если известна одна сторона треугольника и два прилежащих к ней угла, то площадь данного треугольника вычисляется, как половина квадрата данной стороны умноженная на дробь, в числителе которой, произведение синусов прилежащих углов, а в знаменателе синус противолежащего угла. Противолежащий угол вычисляется по формуле:
Площадь треугольника вычисляется по формулам:
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла
R — большая полуось
r — малая полуось
π ≈ 3.14
Формула площади эллипса, через полуоси:
Калькулятор, вычислить площадь элипса:
1. Формула площади равнобедренной трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, ( S ):
Формула площади равнобедренной трапеции через стороны и угол, ( S ):
2. Формулы площади равнобедренной трапеции если в нее вписана окружность
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α , β — углы трапеции
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, ( S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
R — радиус вписанной окружности
m — средняя линия
O — центр вписанной окружности
c — боковые стороны
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию ( S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α , β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, ( S ):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
c — боковая сторона
m — средняя линия трапеции
α , β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, ( S ):
5. Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, ( S ):
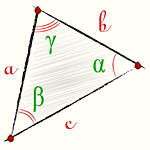
a , b , c — стороны треугольника
α , β , γ — противолежащие углы
Площадь треугольника через сторону и два угла (S):
Формулы для треугольника:
Зная длины всех трех сторон
и используя формулу Герона можно найти площадь разностороннего треугольника
a , b , c — стороны треугольника
p — полупериметр, p=( a + b + c )/2
Формула ( Герона ) площади треугольника через полупериметр ( S ):
Калькулятор — вычислить, найти площадь треугольника:
Формулы для треугольника:
Треугольник это плоская фигура, которая имеет три стороны и три угла. Сумма всех трех углов, равна 180 градусов.
Высота треугольника это — опущенный перпендикуляр из вершины угла на противоположенную сторону или ее продолжение, которую в этом случае, называют основанием.
Что бы найти площадь треугольника,
для этого надо основание умножить на высоту и разделить на два
1. Площадь разностороннего треугольника
h — высота треугольника
Формула площади треугольника (S):
Калькулятор для расчета площади треугольника
2. Площадь треугольника с тупым углом
h — высота треугольника
Формула площади треугольника с тупым углом (S):
Формулы для треугольника:
Зная у треугольника
две стороны и синус угла между ними, находим по формуле, его площадь
a , b , c — стороны треугольника
α , β , γ — углы
Формулы площади треугольника, через две стороны и угол между ними, (S):
Калькулятор — вычислить, найти площадь треугольника:
Формулы для треугольника:
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется — гипотенуза
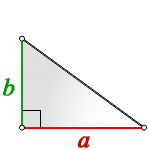
1. Если известны только катеты
a , b — катеты треугольника
Формула площади треугольника через катеты ( S ) :
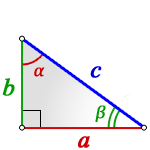
2. Если известны острый угол и гипотенуза или катет
c — гипотенуза
a , b — катеты
α , β — острые углы
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если
то справедливы следующие тождества:
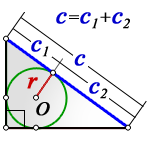
3. Если известны радиус вписанной окружности и гипотенуза
c — гипотенуза
c 1 , c 2 — отрезки полученные делением гипотенузы, точкой касания окружности
r — радиус вписанной окружности
О — центр вписанной окружности
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b , (S):
Калькулятор — вычислить, найти площадь треугольника через высоту и основание:
Формула площади треугольника через, стороны a , b , (S):
Калькулятор — вычислить, найти площадь треугольника через равные стороны и основание:
b — основание треугольника
a — равные стороны
h — высота
Формулы для треугольника:
Если вы знаете сторону или высоту
вы можете найти площадь равностороннего треугольника
a — сторона треугольника
h — высота
Площадь треугольника через сторону a и высоту h , (S):
Площадь треугольника только через сторону a , (S):
Калькулятор для расчета площади равностороннего треугольника
Площадь треугольника только через высоту h , ( S ):
Калькулятор для расчета площади равностороннего треугольника
a — сторона треугольника
h — высота
Формулы для треугольника:
Формула площади круга, диаметр
Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга — отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга — отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса
или радиус круга или длину окружности, можно найти его площадь.
r — радиус круга
D — диаметр круга
Формула площади круга, (S):
на тему: Площадь круга
Калькулятор для расчета площади круга через радиус
Калькулятор для расчета площади круга через диаметр
L — длина окружности
О — центр круга
Формула площади круга если известна длина окружности, (S):
на тему: Площадь круга
Калькулятор для расчета площади круга через длину
Площадь кольца равна — число π , умноженное на разницу квадратов, радиуса внешней окружности и радиуса внутренней окружности
R — радиус внешней окружности
r — радиус внутренней окружности
Формула площади кольца (S):
Калькулятор — вычислить, найти площадь кольца
R — радиус внешней окружности
r — радиус внутренней окружности
α — угол сектора AOB, в градусах
Формула площади сектора кольца (S):
R — радиус круга
α — угол сегмента в градусах
Формула площади сегмента круга (S), отсекаемая хордой AC :
Калькулятор для расчета длины дуги окружности :
Формулы для окружности и круга:
Найти площадь сектора круга если даны радиус и длина дуги или радиус и центральный угол
r — радиус круга
L — длина дуги AB
α — угол сектора круга AOB в градусах
Формула площади сектора круга (S), через длину дуги ( L ):
Формула площади сектора круга (S), через угол ( α ):
Формулы для окружности и круга:
Вычислить площадь ромба, зная: (диагонали) или (сторону и угол между ними) или (диагональ и угол между сторонами)
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы площади ромба через диагонали и углы между сторонами ( S ):
a — сторона ромба
h — высота
r — радиус вписанной окружности
Формула площади ромба через высоту или радиус вписанной окружности ( S ):
1. Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α , β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, ( S ):
Калькулятор — вычислить, найти площадь параллелограмма:
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
H b — высота на сторону b
H a — высота на сторону a
Формула площади через стороны и высоты параллелограмма, ( S ):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d —меньшая диагональ
α , β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , ( S ):
Калькулятор — вычислить, найти площадь параллелограмма:
Формулы для параллелограмма:
http://mozgan.ru/Geometry/AreaTriangle
http://www-formula.ru/2011-09-21-23-43-54/24-elementgeom/ploshadploskfigur
I. Площадь треугольника через синус

Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По таблице синусов синус угла в 30° равен 0.5
Площадь треугольника будет равна 3 кв. см.
| Сторона a= | Сторона b= | Угол γ ° | |
| Ответ: Площадь треугольника = 3.000 |
Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то:
Площадь будет равна половине квадрата стороны, умноженной на дробь. В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:
Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол:
Подставляем данные в формулу
Получаем, что площадь треугольника равняется 3,87 кв. см.
II. Площадь треугольника через косинус
Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать формулу Герона.
По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.
Из теоремы выводим формулы для поиска длины неизвестной стороны:
Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.
Пример расчета формулы площади треугольника через косинус
Дан треугольник с известными сторонами a = 3, b = 4, и углом γ= 45°. Для начала найдем недостающую сторону с. По таблице косинусов косинус 45°=0,7. Для этого подставим данные в уравнение, выведенное из теоремы косинусов.
Теперь используя формулу, найдем площадь треугольника по трем сторонам:
| Сторона a= | Сторона b= | Угол γ ° | |
| Ответ: Площадь треугольника = 4.243 |
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется — гипотенуза
1. Если известны только катеты
a, b — катеты треугольника
Формула площади треугольника через катеты ( S ) :
2. Если известны острый угол и гипотенуза или катет
c — гипотенуза
a, b — катеты
α, β — острые углы
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если
то справедливы следующие тождества:
3. Если известны радиус вписанной окружности и гипотенуза
c — гипотенуза
c1, c2 — отрезки полученные делением гипотенузы, точкой касания окружности
r — радиус вписанной окружности
О — центр вписанной окружности
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :
- Подробности
-
Опубликовано: 07 сентября 2011
-
Обновлено: 13 августа 2021

Свойства треугольников.
Тригонометрия в прямоугольных треугольниках.
Что такое синус/косинус.
Таблицы Брадиса. Как пользоваться.
Теорема синусов и косинусов.
Геометрия — это искусство хорошо рассуждать на плохо выполненных чертежах.
Г. Абель
С основными свойствами разобрались, теперь рассмотрим формулы и их приминение.
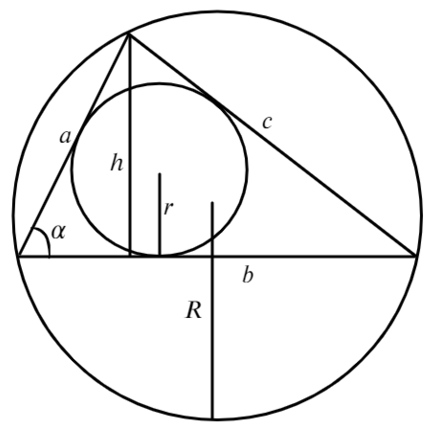
Площадь произвольного треугольника
Нет, это не кривая пентаграмма, нужны на этом рисунке только обозначения. Рассмотрим формулы школьной программы.

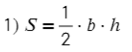
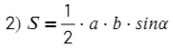
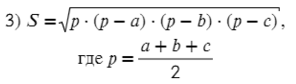
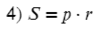
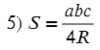
Полезные формулы для прямоугольного и равностороннего треугольника:
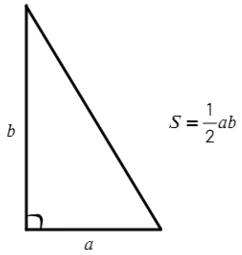
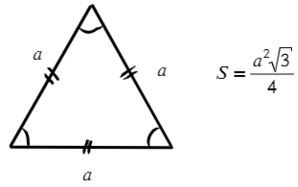
Задача №1. Дано на рисунке:
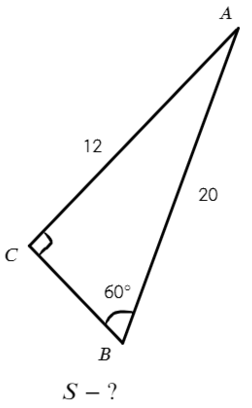
Вариантов здесь много (можно через т. Пифагора), но самый быстрый — найти ∠А = 180°− 90° − 60° = 30°, тогда площадь найдем по (2) формуле: S = ½absinα
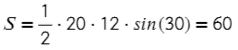
Задача №2. Дано на рисунке:
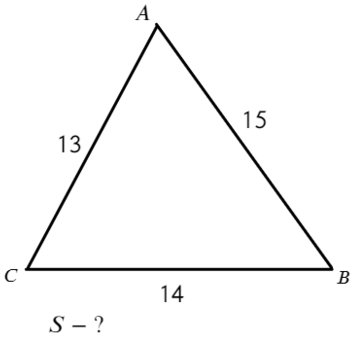
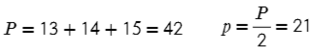
Главное — правильно определиться с формулой.
Ответ: 84
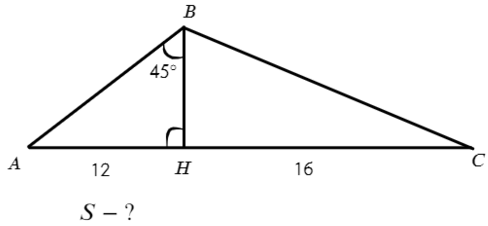
Задача №3. Дано на рисунке:
В ΔABH: ∠A = 180°− 90° − 45° = 45°, значит, ∠A = ∠B => BH = AH = 12.
Тогда площадь можно найти по формуле (1) S=½bh. Высота AH = 12, основание AC = 16+12 = 28. => S = ½×12×28 = 168
Ответ: 168.
Задача №4. Дано на рисунке:
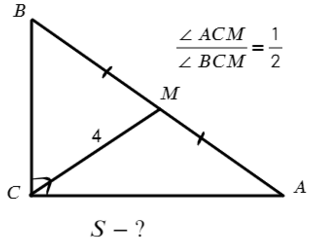
∠ACM = х = 30° => ∠ВCM = 60°. А что у нас равно 4-ем? Да, медиана! А медиана, проведенная из прямого угла, равна половине гипотенузы (2−ое свойство). Тогда отметим равные углы:
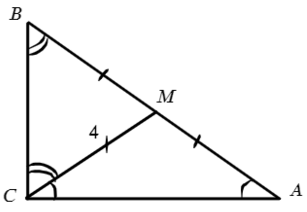
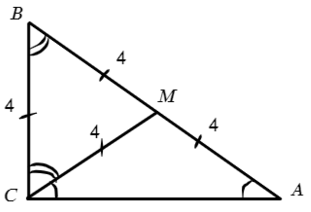
Ответ: 8√3
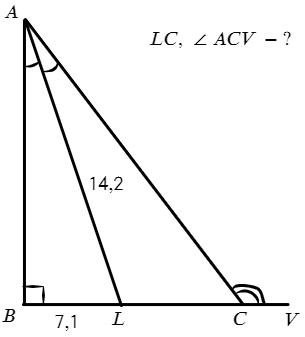
Задача №5. Дано на рисунке:
В дано есть только стороны, а найти нужно угол. Как это сделать? Вот стороны 14,2 и 7,1 во сколько раз отличаются? Да, в 2 раза, а значит угол ∠BAL = 30° (против угла в 30° лежит катет, который в два раза меньше гипотенузы).
Значит, ∠A = 60° => ∠ACB = 180° − 90° − 60° = 30°, а ∠ACB — смежный с ∠ACV => ∠ACV = 180° − 30° = 150°.
Что касается LC: внимательно рассмотрим ΔALC, можно даже лупой воспользоваться. Что видишь? ∠LAC = ∠ACL = 30° => ΔALC — равнобедренный, LC = AL = 14,2.
Ответ: 14,2 и 150°
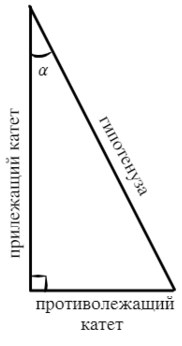
Тригонометрия в прямоугольных треугольниках
В прямоугольном треугольнике три стороны: 2 катета и гипотенуза.
Катеты меньшие стороны треугольника. Гипотенуза большая сторона, которая лежит напротив угла в 90°.
Относительно угла α:
Катет, который составляет угол, называют прилежащим. Катет, который находится напротив угла, называют противолежащим. Логично? Замечательно!
Тригонометрические функции (синус, косинус…) задают связь между углом и длинами сторон.
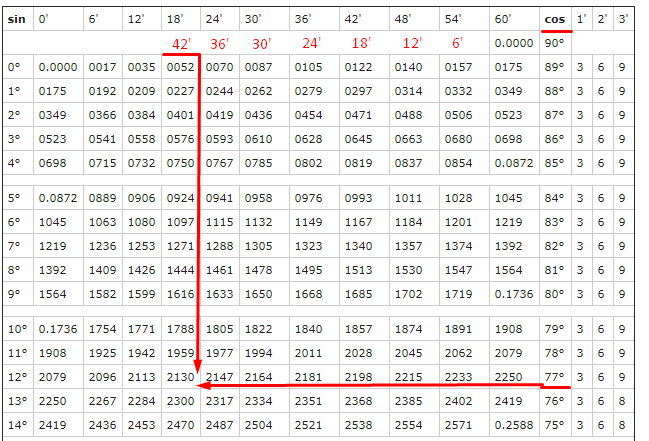
Но хорошо бы знать какие-то значения тригонометрических функций при определенных углах. Все значения вместе образуют таблицу Брадиса. С ее помощью можно вычислить почти любое значение тригонометрической функции при заданом угле. Но как с ней работать?
Найдем sin(10°). Для этого выберем столбец sin и в нем найдем 10°. Ближайшее значение — это то, что нам нужно — 0,1736.
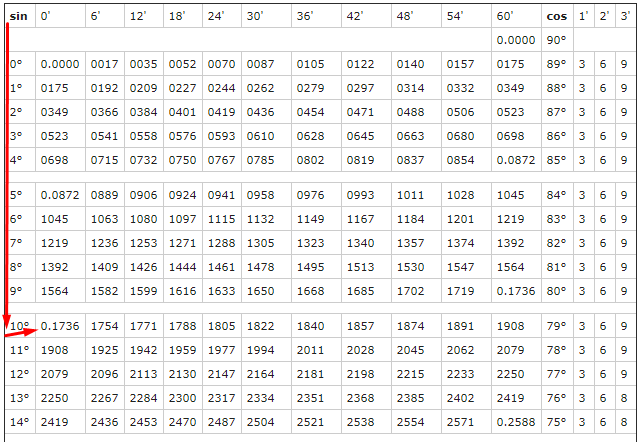
Из общего: и те, и другие минуты измеряются в промежутке от 0 до 60.
Градусные минуты делят один градус на 60 минут (1°=60′), нужны они для большей точности задания угла.
p.s. Есть еще и градусные секунды, и в одной градусной минуте 60 градусных секунд, знакомо? 1° = 60′ = 3600».
Найдем cos(77,7°)
Семь десятых градуса нужно перевести в минуты. Можно через пропорцию:
Теперь в таблице нужно найти 77°42′ для косинуса. Для синуса минуты прописаны, а для косинуса нет. Но мы же люди не гордые, сами напишем, но в обратном порядке. На пересечении 77° и 42′ получаем наше значение:
Но чтобы не загромождать таблицу 0, его в начале пишут только в первых строчках, поэтому ответ cos(77,7°) = 0,213.
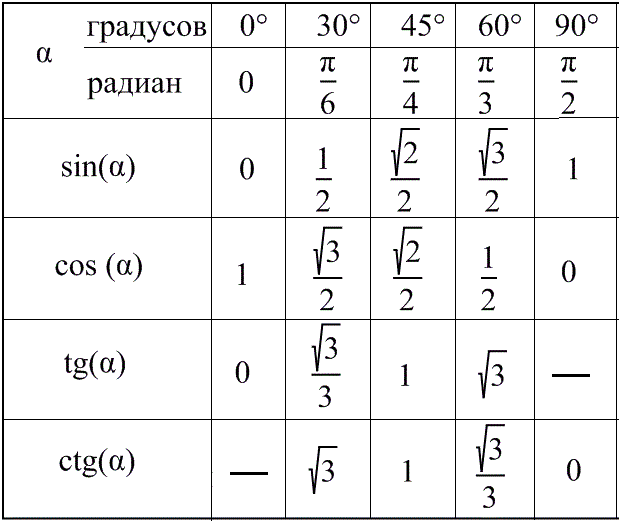
В задачах же таким обилием углов похвастаться нельзя, достаточно знать значения для 30°; 45°; 60°; 90°.
Искусство решать геометрические задачи чем-то напоминает трюки иллюзионистов — иногда,
даже зная решение задачи, трудно понять, как можно было до него додуматься.
И.Д. Новиков
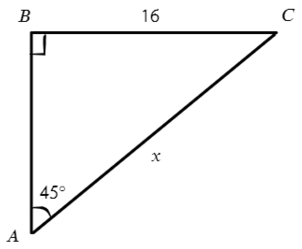
Задача №6. Дано на рисунке:
В этой задаче известен противолежащий катет относительно угла в 45°, а найти нужно гипотенузу. Смотрим, где у нас есть противполежащий катет и гипотенуза? Это синус!
Смотрим в таблице, чему равен синус 45°, и подставляем в отношение:
Ответ: 16√2
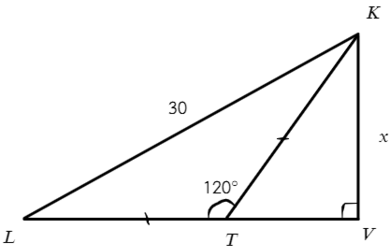
Задача №7. Дано на рисунке:
Мы разобрались с тригонометрическими функциями в прямоугольных треугольниках, значит, и в этой задаче нужно перейти к прямоугольному треугольнику.
В ΔLTK — равнобедренный : ∠L = ∠LKT = (180° − 120°)/2 = 30°
Отлично, в прямоугольном ΔLVK: ∠L = 30° и известна гипотенуза, а нам нужно найти противолежащий катет, чем воспользуемся? Опять синусом!
Ответ: 15
Теорема синусов и теорема косинусов
Сразу возникает вопрос, а теорема тангенсов тоже есть? Конечно, есть, но она очень редко используется.
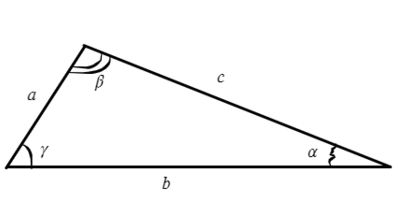
Для любого треугольника можно записать такое соотношение, это будет теорема синусов:
Запомни, что сторона относится к синусу противолежащего угла.
Следствие из теорма синусов гласит, что любое соотношение равно двум радиусам описанной окружности:
Для любого треугольника можно записать такое соотношение, это будет теорема косинусов:
А что будет, если α = 90°, а cos(90) = 0? Получится:
Теорема Пифагора, вот так просто можно запомнить теорему косинусов. Начать как теорему Пифагора, а затем вычесть удвоенное произведение на косинус угла между ними.
Можно записать и для других сторон в этом же треугольнике:
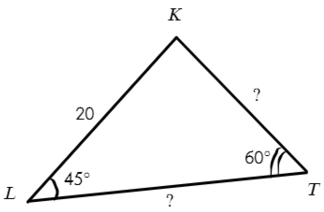
Задача №8. Дано на рисунке:
Запишем теорему синусов для двух отношений:
Выразим отсюда KT:
∠K = 180° − 60° − 45° = 75°. Чтобы найти синус угла 75°, советую посмотреть эту статью, нужно воспользовать формулой суммы синусов:
Тогда представим 75° в виде двух табличных значений:
Аналогично выразим LT:
Ответ: 16,3 и 22,3
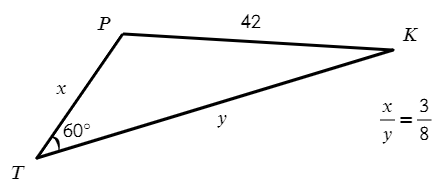
Задача №9. Дано на рисунке:
Найти нужно x и y. Запишем теорему косинусов для этого треугольника:
Икс выразим через игрек:
Ответ: 48; 18
Отлично, поздравляю тебя с Elementary по геометрии!
Что нужно знать:
- Вертикальные, смежные, соответственные, накрест лежащие углы.
- Равенство и подобие треугольников.
- Что такое медиана, биссектриса, высота.
- Свойства треугольников.
- Площадь треугольников.
- Синус/косинус в треугольнике.
- Теорему синусов и косинусов.
Задачи для закрепления по треугольникам
Нашел опечатку, или что-то непонятно — напиши.
Группа с полезной информацией и легким математическим юмором.
Треугольник – это фигура, имеющая три стороны и три угла. Если один из углов треугольника равен 90°,
то он называется «прямоугольным». При этом две стороны, образующие прямой угол – это катеты.
Гипотенуза – это третья сторона, которая находится напротив прямого угла и соединяет катеты между
собой, образуя замкнутую геометрическую фигуру.
- Площадь прямоугольного треугольника через две стороны
- Площадь прямоугольного треугольника через гипотенузу и
острый угол - Площадь прямоугольного треугольника через гипотенузу и
острый угол. Способ 2 - Площадь прямоугольного треугольника через катет и острый
угол - Площадь прямоугольного треугольника через катет и
прилегающий острый угол - Площадь прямоугольного треугольника через гипотенузу и
радиус вписанного круга - Площадь прямоугольного треугольника через гипотенузу и
диаметр вписанного круга - Площадь прямоугольного треугольника через гипотенузу и
площадь вписанного круга - Площадь прямоугольного треугольника через гипотенузу и
длину вписанной окружности (периметр) - Площадь прямоугольного треугольника через касание вписанной
окружности которая делит гипотенузу на части - Площадь прямоугольного треугольника по формуле Герона
- Площадь прямоугольного треугольника через гипотенузу и
высоту
Через две стороны
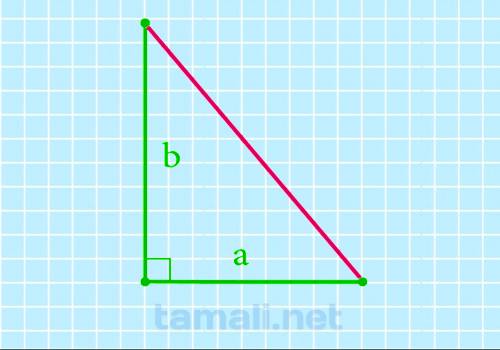
Если в геометрической фигуре известна длина катетов, то можно вычислить площадь фигуры через них. В
некоторых учебниках вертикальный катет называется высотой и обозначается буквой h, но это не
обязательно. При написании формулы можно использовать буквенные обозначения a и b.
S = ½ (a · b)
Цифр после
запятой:
Результат в:
Один из самых простых линейных вариантов вычисления — через две стороны, то есть через два
катета, прилегающих к прямому углу. В этом случае площадь равна половине произведения катетов.
Через гипотенузу и острый угол
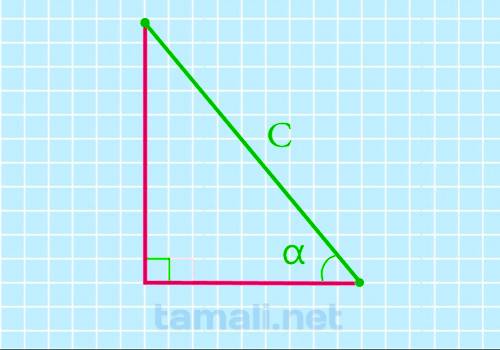
Так как один угол, от которого отходят два катета «а» и «b» равен 90°, два остальных будут острыми.
Эти углы образуются в местах соединения катетов с гипотенузой. Для того, чтобы рассчитать итоговую S
по гипотенузе и острому углу, нужно сначала через длину сторон вычислить sin (синус) и cos
(косинус). Углы в прямоугольном треугольнике обозначаются греческими буквами α (альфа) – угол 90° и
β (бетта) – один из острых углов. Если удается вычислить sin и cos, то через них можно вычислить
площадь по следующей формуле:
S = ¼ · с² · sin(2α)
Цифр после
запятой:
Результат в:
Чтобы вычислить sin α, нужно сторону фигуры «a» (то есть высоту) разделить на гипотенузу: sin α= a /
c.
Чтобы вычислить cos α, нужно сторону «b» разделить на гипотенузу: cos α= b / c.
В данных формулах
гипотенуза обозначается буквой «с». Таким образом выглядят формулы sin и cos для угла α. Точно таким
же образом можно сделать расчеты и для угла β, но даже это не обязательно, потому что в
прямоугольном треугольнике cos α = sin β, а sin α = cos β.
Через гипотенузу и острый угол. Способ 2
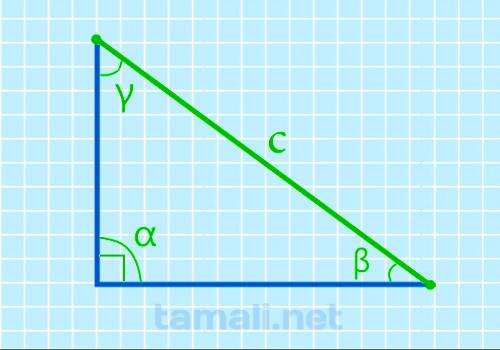
Для данного расчета также понадобятся синусы всех углов треугольника. Нужно вычислить по уже знакомым
формулам sin α= a / c и sin β= b / c. Также понадобится синус третьего угла, который обозначается
греческой буквой γ (гамма). Синус угла γ рассчитывается из разницы между суммой всех углов (180°)
треугольника и суммы двух других углов, а именно: sin (γ) = 180 – (α + β). Также понадобится длина
гипотенузы, которая будет обозначена буквой «C».
Исходя из всех известных величин, формула
площади треугольника через гипотенузу и острый угол следующая:
S = c²/2 * (sin(γ) * sin(β) / sin(α))
Цифр после
запятой:
Результат в:
Через катет и острый угол
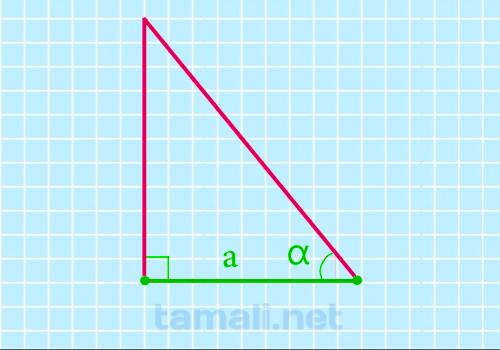
Зная длину катетов, также можно легко вычислить площадь, но в два этапа. Для этого понадобится
предварительно найти tg (тангенс) одного из углов. Например, tg α можно рассчитать по формуле tg α =
a/b, где «a» – это высота (вертикальный катет), а «b» – второй (горизонтальный) катет. Для того,
чтобы вычислить tg угла β, в формуле нужно поменять местами стороны: tgβ = b/a.
Так, формула вычисления площади прямоугольника через катет и острый угол выглядит следующим образом:
если известна сторона «а» —
S = (a² * tgβ) / 2
Если известна сторона «b», то вместо a подставить b.
Цифр после
запятой:
Результат в:
Через гипотенузу и радиус вписанного круга
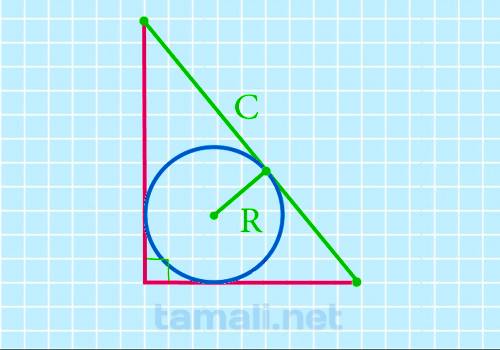
Внутри вписанного круга есть точка (центр круга), которая равноудалена от обоих катетов и гипотенузы.
Прямая от этой точки и до катета, проведенная под прямым углом, — это r (радиус) окружности.
Математически его можно рассчитать по формуле r = (a + b – c) / 2. После того, как радиус стал
известен, площадь можно вычислить через него:
S = r (r + c)
Цифр после
запятой:
Результат в:
Через гипотенузу и диаметр вписанного круга
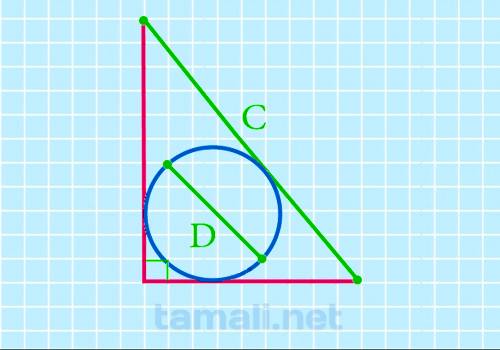
Если d (диаметр) вписанного круга неизвестен, его можно рассчитать следующим образом: d = a + b – c.
Если в условии задачи известен радиус r вписанной окружности, то для вычисления диаметра его можно
умножить на 2, так как d = 2r. Формула площади при известном размере диаметра будет следующая:
S = d/2 * (d/2 + c)
Цифр после
запятой:
Результат в:
Через гипотенузу и площадь вписанного круга
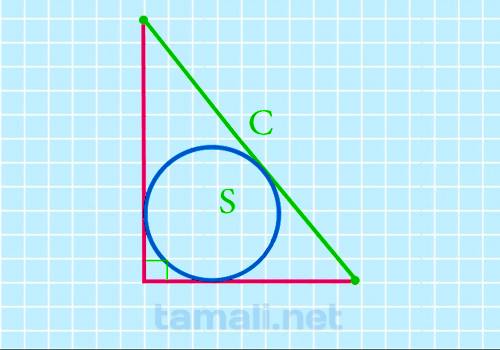
Для этой формулы понадобится знать площадь вписанного круга. Если в условиях задачи она неизвестна,
но вычисляется она по следующей формуле: S = π · r², где π – это математическая константа, равная в
сокращении 3,14, а r – радиус круга. Таким образом, зная площадь круга, можно рассчитывается площадь
треугольника:
S = √(S/π) * (√(S/π)+C)
Цифр после
запятой:
Результат в:
Через гипотенузу и длину вписанной окружности (периметр)
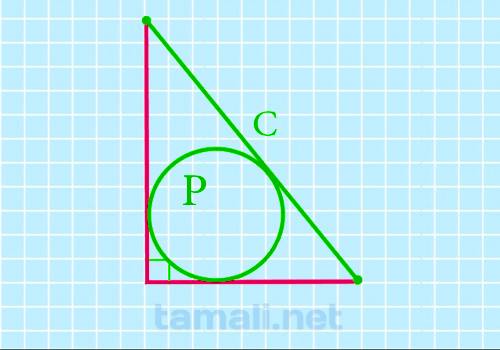
Чтобы найти периметр окружности для главной формулы площади треугольника, нужно знать либо диаметр
окружности, либо радиус. Периметр в данном случае обозначается латинской буквой P. Формулы буду
следующие: если известен диаметр окружности P = d · π, если известен радиус окружности P = 2 · r ·
π.
Зная периметр вписанной окружности, можно рассчитать площадь прямоугольного треугольника по
следующей формуле:
S = P/2π * (P/2π + C)
где C – это гипотенуза треугольника, π – это математическая константа, равная в сокращении 3,14, и
периметр окружности P.
Цифр после
запятой:
Результат в:
Через касание вписанной окружности которая делит гипотенузу на части
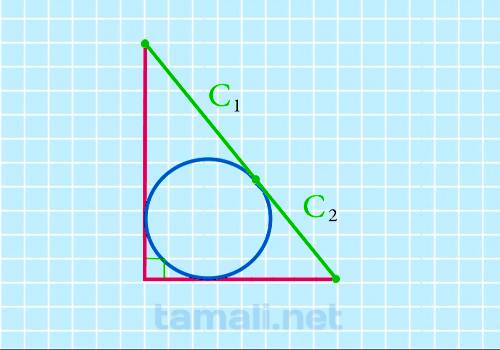
Если внутри прямоугольного треугольника нарисовать окружность, центр которой будет равноудален от
катетов и гипотенузы, она разделит гипотенузу на два отрезка, которые условно обозначаются С1 и С2.
С их помощью, не зная других величин, можно вычислить площадь треугольника:
S = C1 · C2
Цифр после
запятой:
Результат в:
Площадь прямоугольного треугольника по формуле Герона
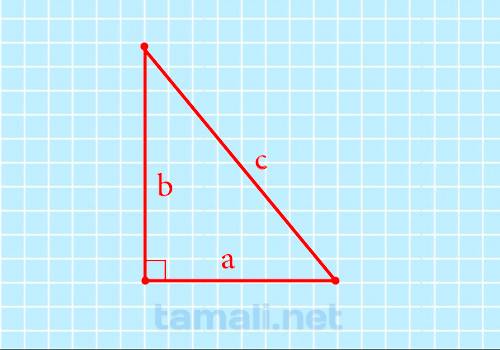
Для вычисления площади по методу Герона понадобится значение полупериметра, который обозначается
маленькой латинской буквой «p» (полный периметр обозначается заглавной Р). Полупериметр – это
половина суммы всех сторон, а именно: p = (a + b + c)/2, где a и b – это катеты, а С –
гипотенуза.
После того, как полупериметр вычислен, можно переходить к основной формуле площади прямоугольного
треугольника. Для того, чтобы ее найти, нужно рассчитать корень квадратный из следующих величин:
S = (P — a) * (P — b)
Цифр после
запятой:
Результат в:
Герон Александрийский был математиком во времена Римской империи. Одним из направлений его
деятельности была так называемая «Метрика» и ее подраздел «Геометрика», по которым ученый написал
большую энциклопедию. В содержании этой книги, в том числе, была также формула вычисления площади
прямоугольного треугольника по длинам его сторон. Впервые этот метод определения площади был
установлен еще Архимедом, но конкретную формулу вывел именно Герон, предположительно в I веке до
н.э.
Через гипотенузу и высоту
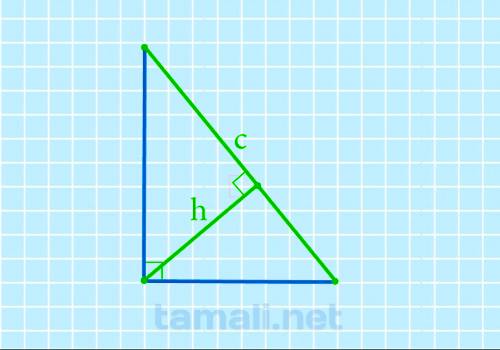
Высота – это прямая, соединяющая точку пересечения катетов с гипотенузой под углом 90°. При этом
высота разделяет прямоугольный угол треугольника на два равных по 45° каждый. Обозначается данная
величина латинской буквой h. Формула площадки треугольника через гипотенузу и высоту простая и
линейная:
S = ½ch
Цифр после
запятой:
Результат в:
Через катет и прилегающий острый угол
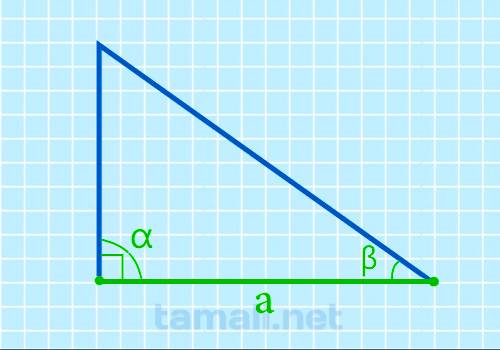
Для составления данной формулы нужно определиться с наименованием сторон и углов. Например, нижний
катет треугольника (горизонтально расположенный), будет называться стороной «a». Слева от него
находится прямой угол в 90°, под условным обозначением α, а справа от катета «a» находится
прилегающий острый угол β.
Для итоговой формулы также понадобятся синусы углов. Таким образом, sin α= a / c и соответственно sin
β= b / c. После того, как эти величины будут найдены, можно переходить к основной формуле:
S = a²/2 * (sin(α) * sin(β)/sin(180-(α+β))
где 180° — это сумма всех углов треугольника.
Цифр после
запятой:
Результат в:
Когда требуется вычисление площади прямоугольного треугольника
Площадь прямоугольных треугольников напрямую связана с вычислением площади прямоугольников, так как в
них обоих присутствуют углы в 90°. При этом для вычисления нужной величины, можно использовать любой
из вышеперечисленных способов. Выбор зависит только от наличия известных параметров геометрической
фигуры или от выбора самого простого решения. Для того, чтобы уметь пользоваться формулой, нужно
понять логическую цепочку ее вывода и, если не все составляющие уравнения известны, найти способ их
узнать через дополнительные формулы. Зная определенные параметры треугольника, путем различных
вычислений можно рассчитать его площадь.