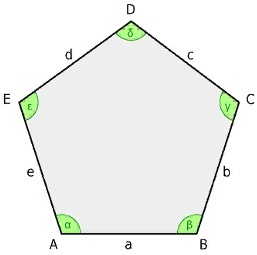
Пятиугольник представляет собой геометрическую фигуру с пятью углами. Существует множество разных пятиугольников, однако если стороны равны, а каждый угол фигуры равен 108 градусам, то многоугольник называется правильным и носит название «пентагон».
Геометрия пятиугольника
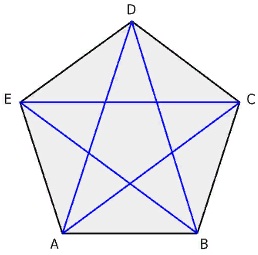
Пятиугольник — это фигура, которая состоит из пяти соединенных отрезков. Стороны произвольного многоугольника могут соединяться под разными углами, в результате чего фигура может быть невыпуклой. Наиболее ярким примером невыпуклого многоугольника является звезда, а пятиугольника — проекция зубчатой короны, когда два «зубца» выступают над прямоугольным основанием. Выпуклый многоугольник — это фигура, продолжение отрезков которого не пересекает других сторон. Если же мы продлим отрезки зубцов или лучей звезды, они пересекут другие стороны фигуры.
Пятиугольник в реальности
Невыпуклые геометрические фигуры редко встречаются в человеческой повседневности и обычно представляют собой основания для нестандартных призм. Наиболее распространенным пятиугольником в реальности считается пентагон — правильный многоугольник. Пентагон нашел применение в архитектуре и дизайне, и тезкой фигуры является одно из самых известных зданий Америки — штаб министерства обороны США.
Додекаэдр — платоново тело, каждая из 12 сторон которого является правильным пятиугольником. Додекаэдр используется в различных сферах, но наиболее известным представлением многогранника считается игральная кость d12, которая используется как генератор случайных чисел для настольных ролевых игр.
Несмотря на то, что многие организмы обладают пентасимметрией, например, морские звезды или плоды мушмулы, природные пятиугольные объекты практически не встречаются в природе.
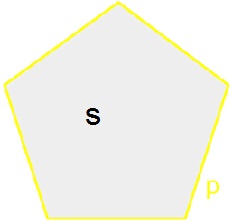
Площадь пентагона
Площадь любой геометрической фигуры — это количественная оценка того, какую часть плоскости ограничивают ее стороны. Площадь правильного пятиугольника рассчитывается по общей для всех правильных многоугольников формуле:
S = n/4 × a2 × ctg(pi/n),
где n – количество сторон фигуры, a – длина стороны.
Таким образом, если подставить n = 5 и выразить получившееся выражение десятичной дробью, мы получим простую формулу для вычисления площади пентагона:
S = 1,72 a2
где a — длина одной стороны.
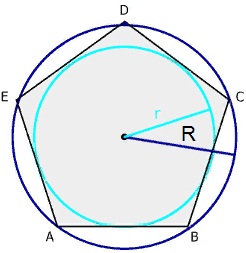
Сторона пентагона и радиусы вписанной r и описанной окружности R приблизительно соотносятся как:
- a = 1,4131 r
- a = 1,1756 R
Программный код калькулятора использует эти соотношения, что позволяет вам найти площадь правильного пятиугольника, зная только один параметр из перечисленных:
- радиус вписанной окружности;
- радиус описанной окружности;
- длина стороны.
Рассмотрим на примерах, как вычислить площадь правильного пятиугольника.
Примеры из жизни
Пентагон
Штаб министерства обороны США — это всемирно известное здание, которое имеет форму правильного пятиугольника. Каждая сторона штаба имеет длину 281 м и мы без проблем можем узнать, какую площадь занимает здание. Для более удобного представления выразим длину в километрах, введем эти данные в форму калькулятора a = 0,281 и получим результат:
S = 0,1359
Площадь Пентагона составит 0,136 квадратных километров.
Школьная задача
К примеру, необходимо вычислить площадь пентагона, зная, что радиус вписанной окружности составляет 15 см. Мы можем выразить сторону многоугольника через простое соотношение радиуса вписанной окружности и длины стороны a = 1,4131 r, после чего посчитать по формуле его площадь. Проще всего ввести значение радиуса в ячейку «Радиус вписанной окружности r» и получить мгновенный результат:
S = 817,36
Кроме непосредственно площади фигуры, калькулятор автоматически подсчитал остальные атрибуты пятиугольника.
Заключение
Пентагон нечасто встречается в реальной жизни, однако при решении производственных вопросов или школьных задач вам может понадобиться рассчитать площадь или периметр правильных многоугольников. Наш каталог калькуляторов к вашим услугам.
Правильном пятиугольнике это многоугольнике с 5 вершинами. Данная форма часто используется при строительстве и в архитектуре. Введите одно из известных значений, затем нажмите кнопку вычислить.
.
Поделиться расчетом:
Калькулятор пятиугольника
Длина стороны(a)
Диагноль(D)
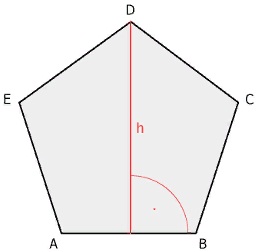
Высота(h)
Периметр(p)
Площадь(S)
Радиус описанной окружности(R)
Радиус вписанной окружности(r)
Вычислить
Очистить
Формулы:
d = a / 2 * ( 1 + √5 )
h = a / 2 * √ 5 + 2 * √5
Р = 5 * а
S = a2 / 4 * √ 25 + 10 * √5
R = a / 10 * √ 50 + 10 * √5
r = a / 10 * √ 25 + 10 * √5
Угол: 72°, 5 сторон.
Формулы:
d = a / 2 * ( 1 + √5 )
h = a / 2 * √ 5 + 2 * √5
p = 5 * a
S = a² / 4 * √ 25 + 10 * √5
re = a / 10 * √ 50 + 10 * √5
ri = a / 10 * √ 25 + 10 * √5
Длина, высота, периметр и радиус имеют одинаковые метрические единицы (например, метры), площадь — те же единицы, возведенные в квадрат (например, квадратный метр).
A closed and flat two-dimensional surfaced shape with five angles and five sides is called as pentagon. Area of a Pentagon is the amount of space occupied by the pentagon. Below given an Area of a Pentagon Calculator that helps you in calculating the area of a five-sided pentagon. Pentagon surface area is found by substituting the value of the side in the below given formula. It can also be calculated using apothem length (i.e) the distance between the center and a side.
A closed and flat two-dimensional surfaced shape with five angles and five sides is called as pentagon. Area of a Pentagon is the amount of space occupied by the pentagon. Below given an Area of a Pentagon Calculator that helps you in calculating the area of a five-sided pentagon. Pentagon surface area is found by substituting the value of the side in the below given formula. It can also be calculated using apothem length (i.e) the distance between the center and a side.
Code to add this calci to your website 
Formula:
A = 1/4 x √(5(5 + 2 x √(5))) x s2
Where,
A = Pentagon Surface Area
s = Side Length

Example
A pentagon having one of its side length as 15 mm.
Area of a Pentagon = 1/4 x √(5(5 + 2 x √(5))) x 152
= 387.1074mm2
Related Calculators:
- Perimeter Of A Pentagon Calculator
- Triangle Side Length Calculator
- Heron’s Formula Calculator
- Radius Of Area Sector Calculator
- Angular Deflection Of Hollow Shaft Calculator
- Pentagon Diagonal Length Calculator
Площадь правильного пятиугольника
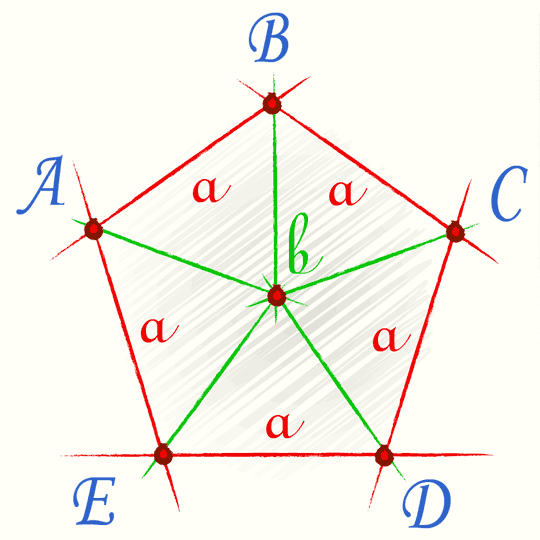
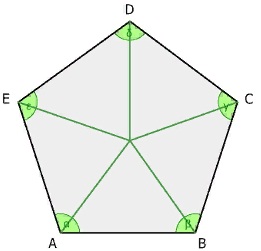
Нарисуем правильный пятиугольник.
Площадь правильного пятиугольника
Как мы видим он состоит из пяти равных равнобедренных треугольников с основанием a и бедрами b.
Если мы знаем только размер стороны a правильного пятиугольника, то размер b легко находится по формуле
радиуса описанной окружности правильного пятиугольника.
Таким образом получаем следующий вывод формулы:
[ b = frac{a}{2 sin(π/5)} ]
[ S_{равнобедр.треуг} = frac{a sqrt{b^2-frac{a^2}{4}}}{2}]
[ S_{равнобедр.треуг} = frac{1}{2} a sqrt{Big(frac{a}{2 sin(π/5)}Big)^2-frac{a^2}{4}}]
[ S = 5 S_{равнобедр.треуг} ]
[ S = frac{5}{2} a sqrt{Big(frac{a}{2 sin(π/5)}Big)^2-frac{a^2}{4}} ]
Вычислить, найти площадь правильного пятиугольника по формуле (5)
Площадь правильного пятиугольника |
стр. 321 |
|---|