Формулировка задачи: Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны A, B и C. Найдите площадь четвёртого прямоугольника.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20 (Задачи на смекалку).
Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.
Пример задачи:
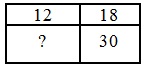
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 12, 18 и 30. Найдите площадь четвёртого прямоугольника.
Решение:
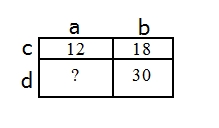
Для удобства дадим название каждой стороне прямоугольника (см. рисунок). И распишем, чему равна площадь каждого маленького прямоугольника по часовой стрелке, начиная с верхнего левого:
S1 = a ⋅ c = 12
S2 = b ⋅ c = 18
S3 = b ⋅ d = 30
S4 = a ⋅ d = ?
Выразим стороны a и d из первой и третьей площади и подставим их в площадь четвертого прямоугольника:
a = 12 / c
d = 30 / b
S4 = 12 / c ⋅ 30 / b
Мы также можем выразить сторону b через вторую площадь, чтобы площадь четвертого прямоугольника была выражена только через одну сторону:
b = 18 / c
S4 = 12 / c ⋅ 30 / 18 ⋅ c = 12 ⋅ 30 / 18 = 20
В результате все неизвестные сократились и была найдена площадь четверного прямоугольника, равная 20.
Ответ: 20
В общем виде решение данной задачи на смекалку выглядит следующим образом:
ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА = A ⋅ C / B
где A , B и C – площади трех других прямоугольников, начиная с левого верхнего и далее по часовой стрелке.
Осталось лишь подставить все значения и получить ответ.
Как найти площадь фигуры, если это прямоугольник с вырезанным куском?
На этой странице сайта вы найдете ответы на вопрос Как найти площадь фигуры, если это прямоугольник с вырезанным куском?,
относящийся к категории Математика. Сложность вопроса соответствует базовым
знаниям учеников 1 — 4 классов. Для получения дополнительной информации
найдите другие вопросы, относящимися к данной тематике, с помощью поисковой
системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и
задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям.
Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы
помогут найти нужную информацию.
Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
Николаич
8 октября, 13:52
Как найти площадь фигуры, если это прямоугольник с вырезанным куском?
-
-
Стюра
8 октября, 15:42
+1
Найди площадь прямоугольника, а потом найди площадь вырезанной фигуры и вычти ее из площади прямоугольника, вот и ответ
- Комментировать
- Жалоба
- Ссылка
Найдите правильный ответ на вопрос ✅ «Как найти площадь фигуры, если это прямоугольник с вырезанным куском? …» по предмету 📘 Математика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Новые вопросы по математике
Главная » Математика » Как найти площадь фигуры, если это прямоугольник с вырезанным куском?
Информация по назначению калькулятора
Прямоугольник — это двумерная геометрическая фигура, имеющая 4 стороны и 4 угла. Две его стороны сходятся под прямым углом. Таким образом, прямоугольник имеет 4 угла, каждый из которых равен 90 градусов. Противоположные стороны прямоугольника имеют одинаковую длину и параллельны. Две стороны называются параллельными, когда расстояние между ними остается одинаковым во всех точках.
Поскольку все углы прямоугольника равны, его можно назвать равноугольным четырехугольником.
Некоторые свойства прямоугольника отмечены далее:
⇒ Прямоугольник — это четырехугольник.
⇒ Противоположные стороны прямоугольника равны и параллельны друг другу.
⇒ Внутренний угол прямоугольника в каждой вершине равен 90°.
⇒ Сумма всех внутренних углов равна 360°.
⇒ Диагонали делят пополам друг друга.
⇒ Длина диагоналей равна.
⇒ Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
⇒ Все прямоугольники являются параллелограммами, но не все параллелограммы являются прямоугольниками.
Онлайн калькулятор поможет найти параметры прямоугольника, такие как:
- Длины сторон
- Периметр
- Площадь
- Диагонали
- Углы
- Радиус Описанной окружности
- Диаметр Описанной окружности
- Длина Описанной окружности
- Площадь Описанной окружности
— равен сумме всех 4х сторон (P=AB+BC+CD+DA)
— равна произведению двух сторон (S=AB*BC)
— Диагональ разрезает прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а две смежные стороны прямоугольника образуют две другие стороны треугольника.(AC=√(AB2 + BC2))
— всегда равны 90 градусов
Диаметр описанной окружности прямоугольника равен длине его диагонали
