Как найти площадь ромба на квадратной бумаге - Исправление недочетов и поиск решений вместе с Examum.ru

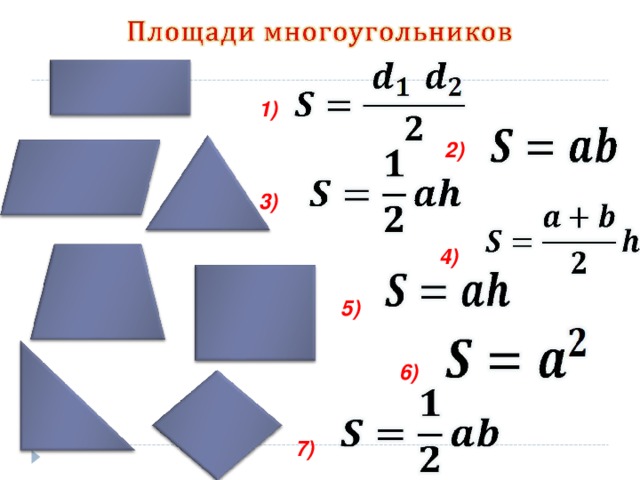
Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

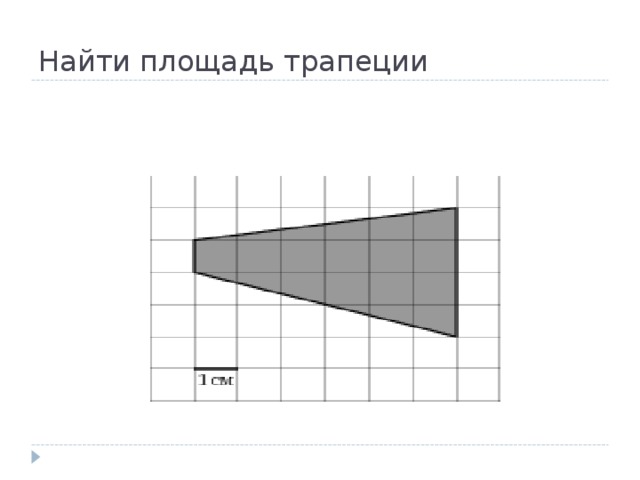
1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

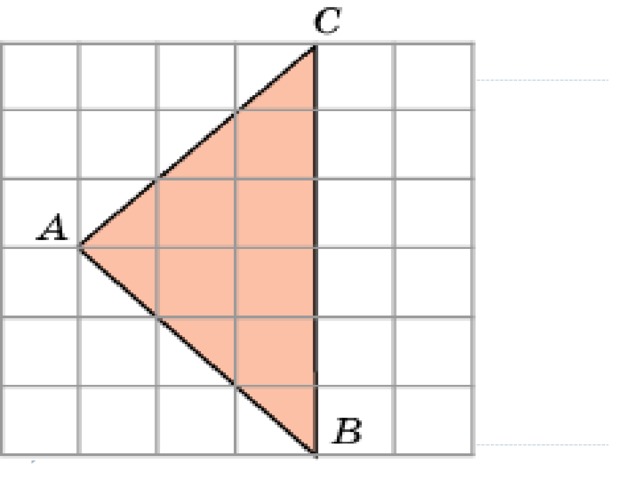
2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

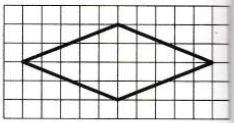
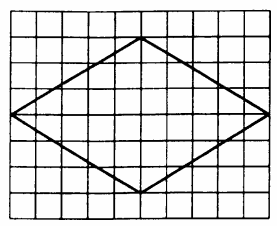
4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

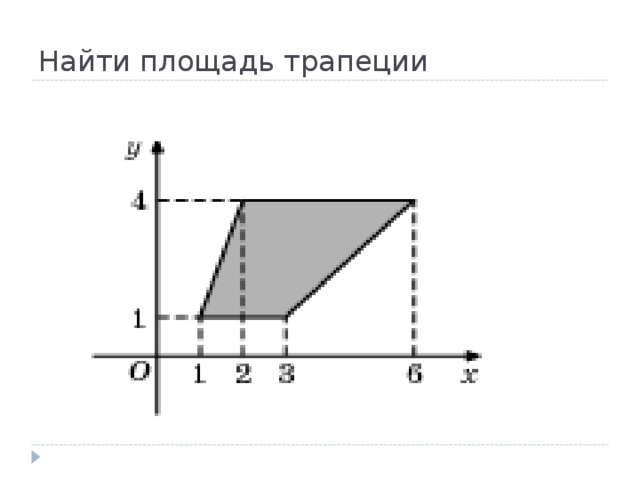
5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

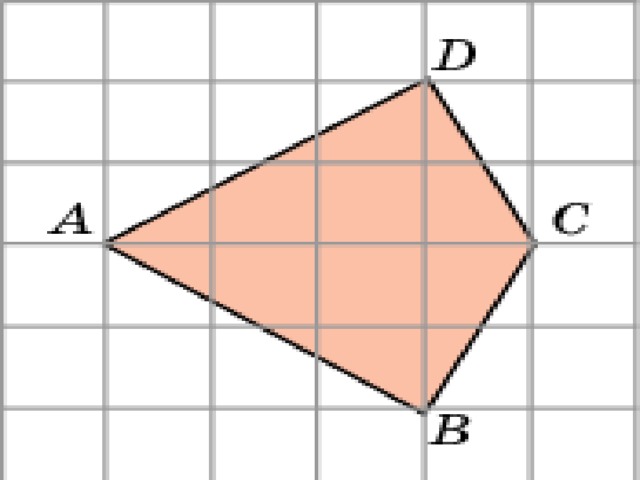
6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

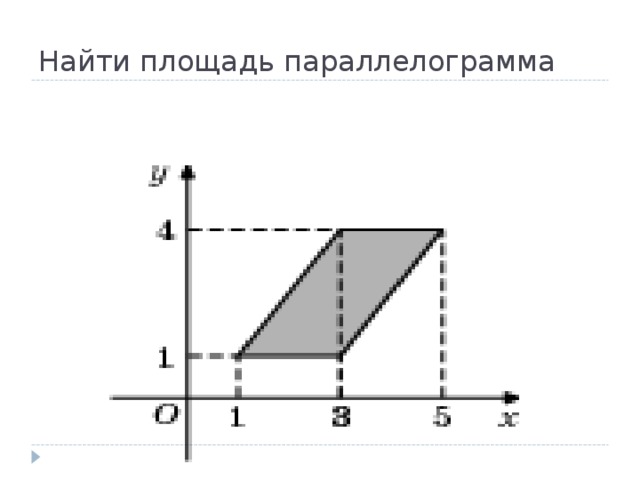
14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

было в ЕГЭ

в условии
в решении
в тексте к заданию
в атрибутах

Категория

Атрибут

Всего: 41 1–20 | 21–40 | 41–41

Добавить в вариант

Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Найдите площадь прямоугольника, изображенного на рисунке.

Найдите площадь параллелограмма, изображенного на рисунке.

Найдите площадь прямоугольника, изображенного на рисунке.

Найдите площадь параллелограмма, изображенного на рисунке.

Найдите площадь квадрата, изображенного на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Найдите площадь параллелограмма, изображенного на рисунке.

Всего: 41 1–20 | 21–40 | 41–41

Источник

Задание 3. ЕГЭ. Найти площадь ромба

Рубрика Задание 3, Решаем ЕГЭ по математике Комментарии (0)

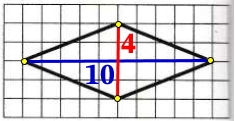
Задание. На клетчатой бумаге с размером клетки 1 × 1 изображен ромб. Найдите его площадь.

Решение:

Площадь ромба равна половине произведения его диагоналей, т. е.

По рисунку находим: AC = 10, BD = 2, тогда

Ответ: 10

Понравилось? Нажмите

Источник

На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.

Источник: ОГЭ Ященко 2022 (36 вар)

Решение:

Площадь ромба находится по формуле, через диагонали:

S=frac{1}{2}cdot d_{1}cdot d_{2}=frac{1}{2}cdot 4cdot 10=2cdot 10=20

Ответ: 20.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.6 / 5. Количество оценок: 41

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Задание:

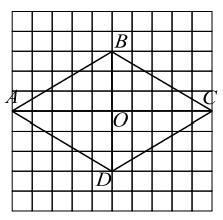
Найдите площадь ромба, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см. Ответ дайте в квадратных сантиметрах.

Решение:

Площадь ромба равна половине произведения его диагоналей. AC = 10, BD = 6, следовательно, SABCD = 1/2 * AC * BD = 30.

Ответ: 30.

Создайте Ваш сайт учителя

Курсы ПК и ППК
Видеоуроки

Олимпиады
Вебинары для учителей

Главная
Математика
Тесты
Проверочная работа по теме «Площадь» в формате ОГЭ (9 класс)

Проверочная работа по теме «Площадь» в формате ОГЭ для 9 класса. Содержит 5 заданий: 1) выбрать верное утверждение; 2) найти площадь фигуры, изображенной на рисунке; 3-5 текстовые задачи на нахождение площади плоских фигур.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

Просмотр содержимого документа

«Проверочная работа по теме «Площадь» в формате ОГЭ (9 класс)»

Предмет: Математика

Категория: Тесты

Целевая
аудитория: 9 класс.
Урок соответствует ФГОС

Автор: Касьянова Наталья Игоревна

Дата: 12.12.2016

Номер свидетельства: 369009

Каталог заданий.
Ромб

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задание 18 № 311333

На рисунке изображен ромб ABCD. Используя рисунок, найдите .

Аналоги к заданию № 311333: 311376 Все

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 2)

Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.

Решение

Сообщить об ошибке · Помощь

Задание 18 № 311376

На рисунке изображен ромб  ABCD. Используя рисунок, найдите  .

Аналоги к заданию № 311333: 311376 Все

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.6)

Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.

Решение

Сообщить об ошибке · Помощь

Задание 18 № 348446

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Аналоги к заданию № 348446: 348586 349027 349478 350071 352059 352113 352152 352709 352791 353130 … Все

Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.

Решение

Сообщить об ошибке · Помощь

Задание 18 № 356974

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Аналоги к заданию № 356974: 356975 356976 356977 356978 356979 401771 402380 402415 402423 402896 … Все

Источник: Банк заданий ФИПИ

Решение

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

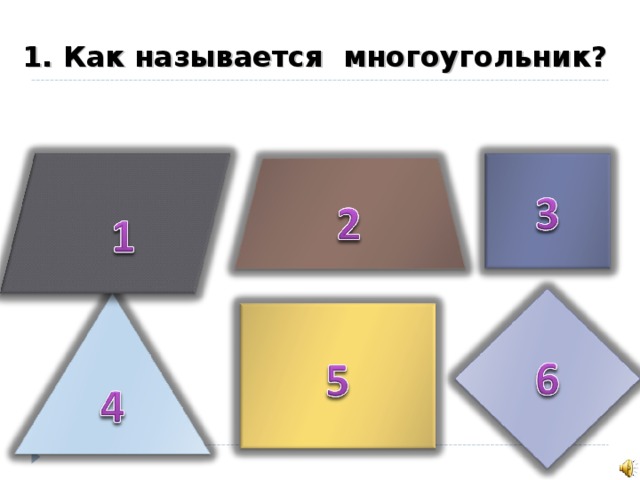
1. Как называется многоугольник?

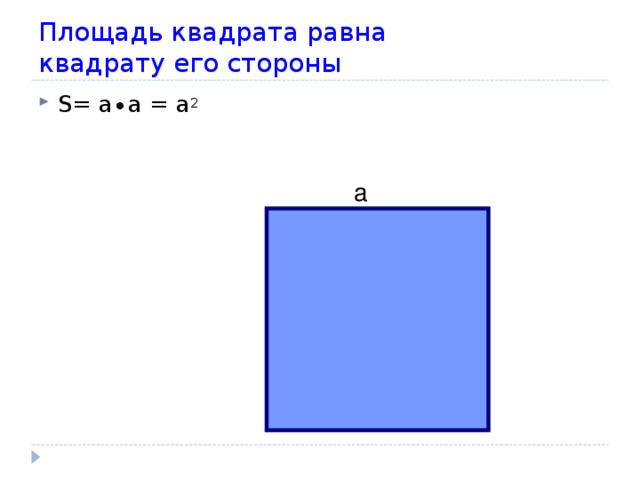
Площадь квадрата равна квадрату его стороны

S= а ∙а = а 2

Площадь прямоугольник равна произведению его смежных сторон

S = a ∙b

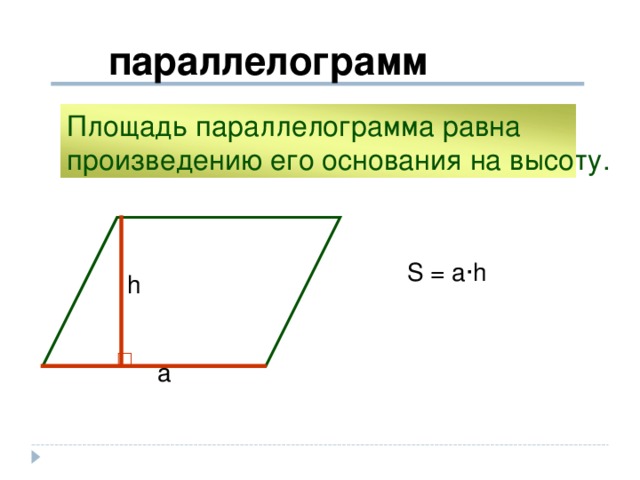
параллелограмм

Площадь параллелограмма равна

произведению его основания на высоту.

S = a ∙h

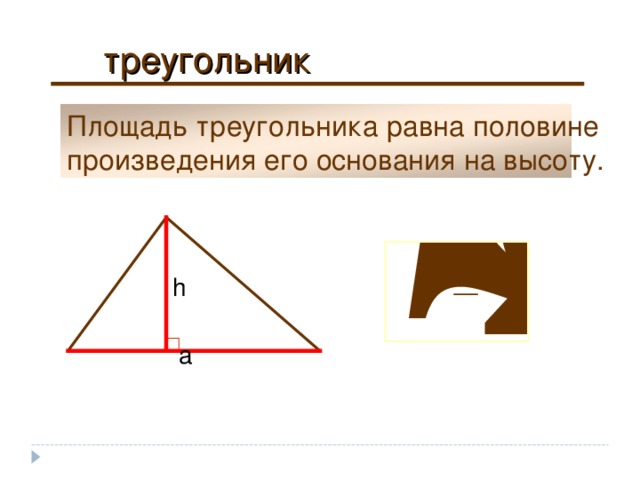
треугольник

Площадь треугольника равна половине

произведения его основания на высоту.

Формула Герона

Площадь треугольника со сторонами a,b,c выражается формулой

где p- полупериметр треугольника

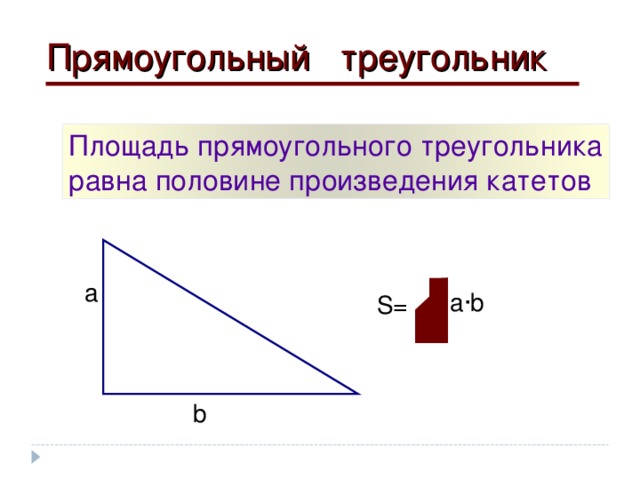
Прямоугольный треугольник

Площадь прямоугольного треугольника

равна половине произведения катетов

a ∙b

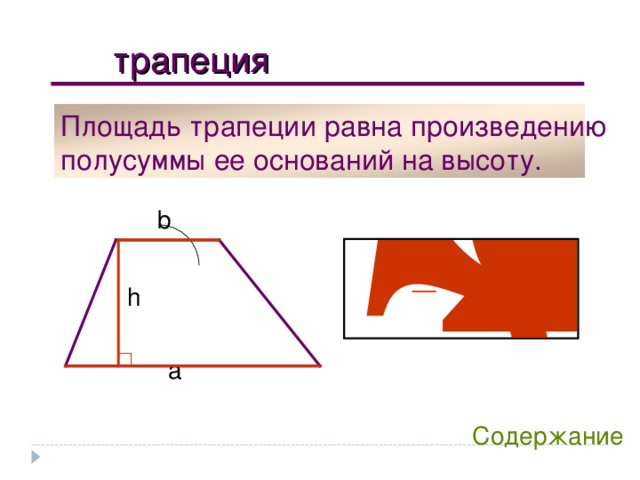
трапеция

Площадь трапеции равна произведению

полусуммы ее оснований на высоту.

Содержание

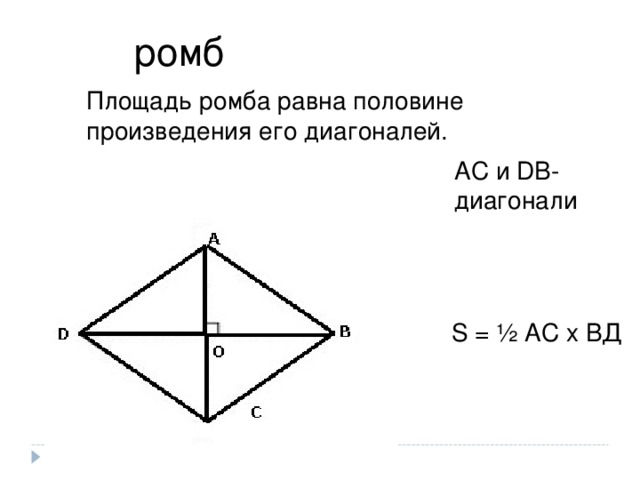
ромб

Площадь ромба равна половине произведения его диагоналей.

AC и DB-

диагонали

S = ½ АС х ВД

Найти площадь прямоугольника:

Задача №1

Найти площадь квадрата:

13см

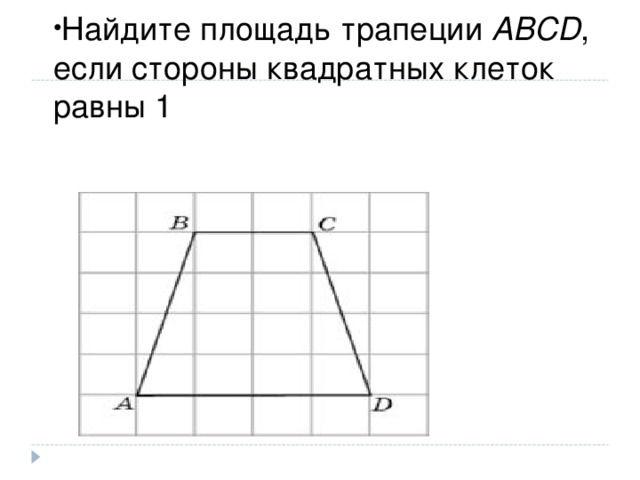
Найдите площадь трапеции ABCD , если стороны квадратных клеток равны 1

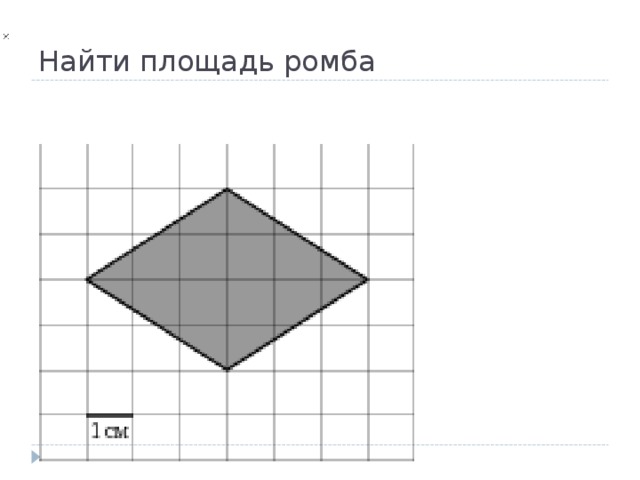
Найти площадь ромба

Найти площадь трапеции

Найти площадь параллелограмма

Найти площадь трапеции

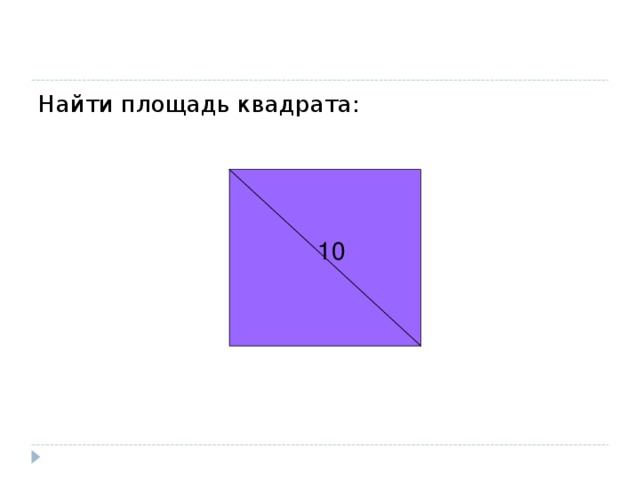
Найти площадь квадрата:

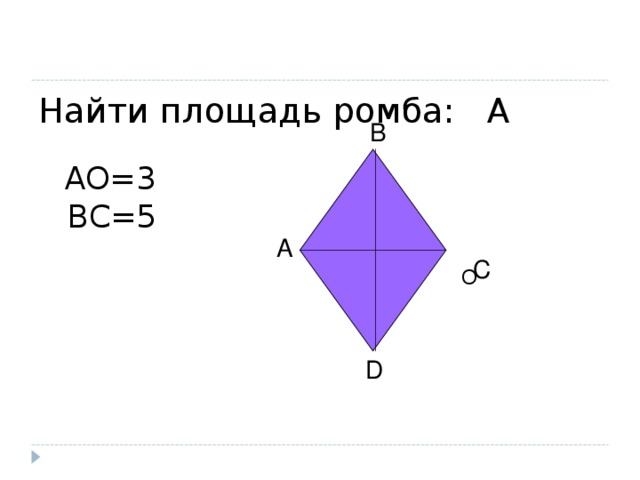
Найти площадь ромба: А

АО= 3

ВС= 5

Найти площадь четырехугольника диагонали, которого перпендикулярны и равны соответственно 14 и 9 :

Найти площадь треугольника со сторонами 9 , 12 и 15:

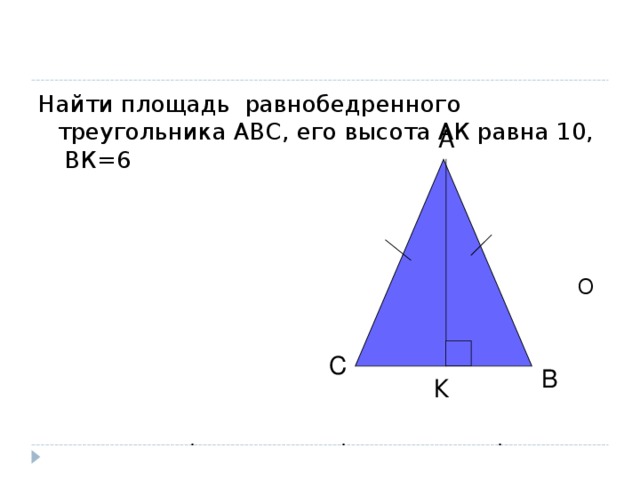
Найти площадь равнобедренного треугольника АВС, его высота АК равна 10, ВК=6

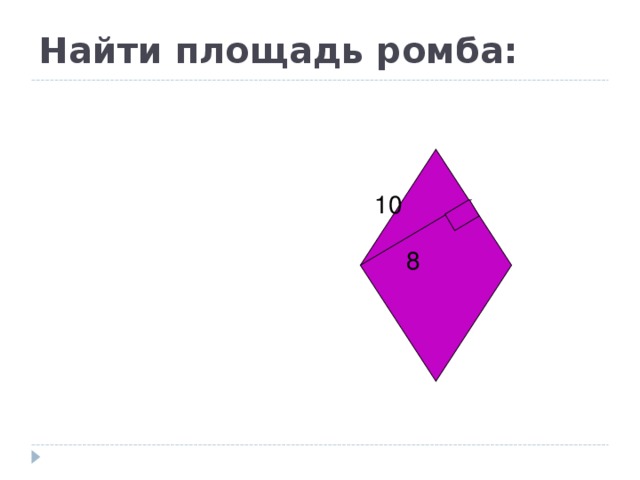
Найти площадь ромба:

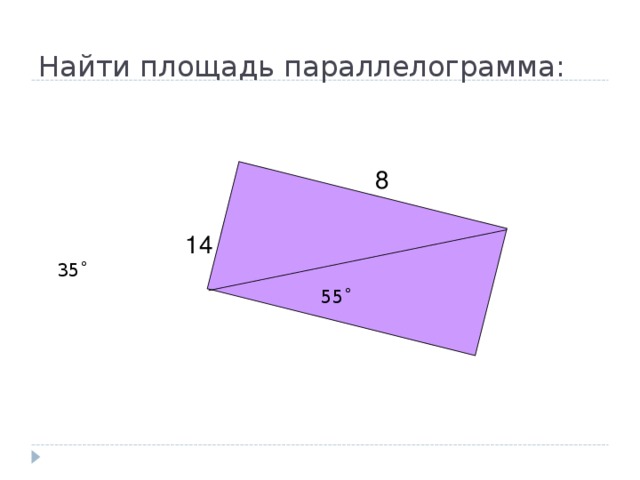
Найти площадь параллелограмма:

35 ˚

55˚

ТЕСТ

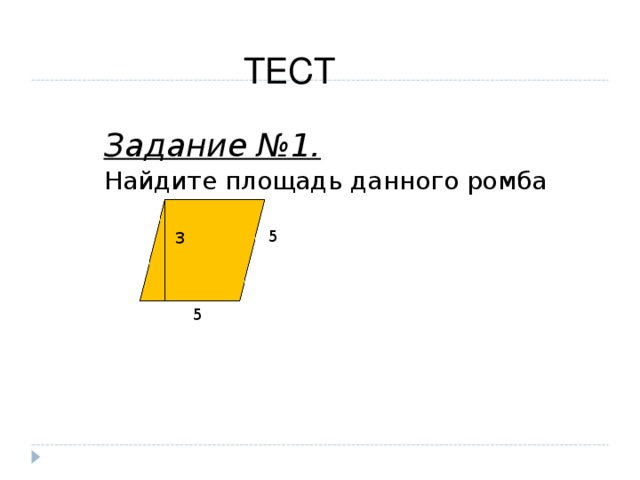
Задание №1.

Найдите площадь данного ромба

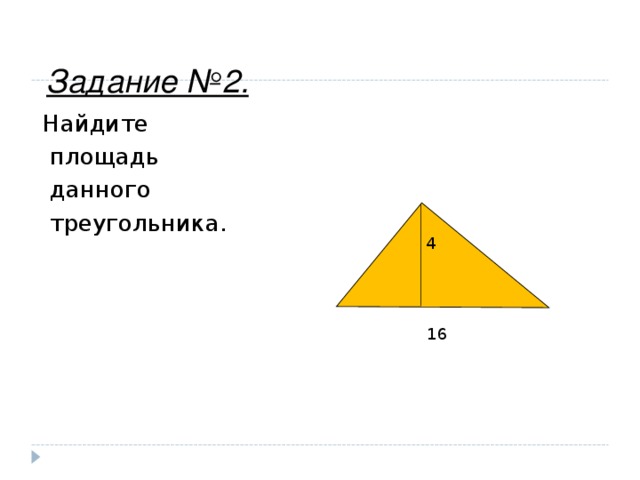
Задание №2.

Найдите

площадь

данного

треугольника.

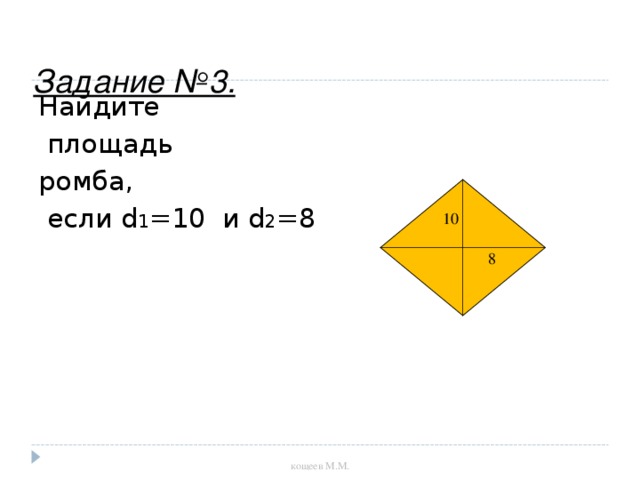
Задание №3.

Найдите

площадь

ромба,

если d 1 =10 и d 2 =8

кощеев М.М.

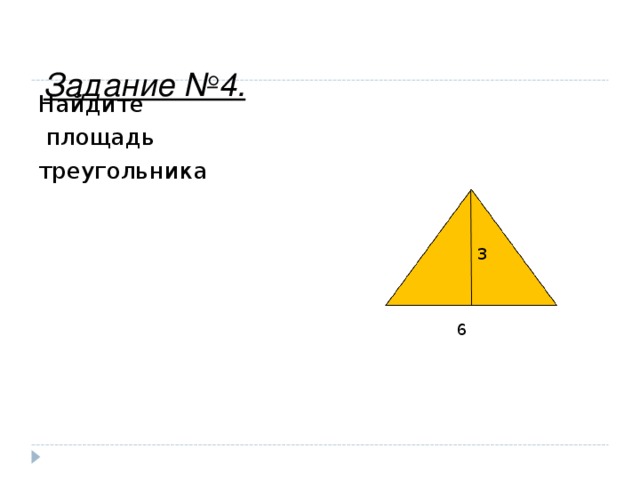
Задание №4.

Найдите

площадь

треугольника

Задание №5.

Найдите площадь прямоугольного треугольника

кощеев М.М.

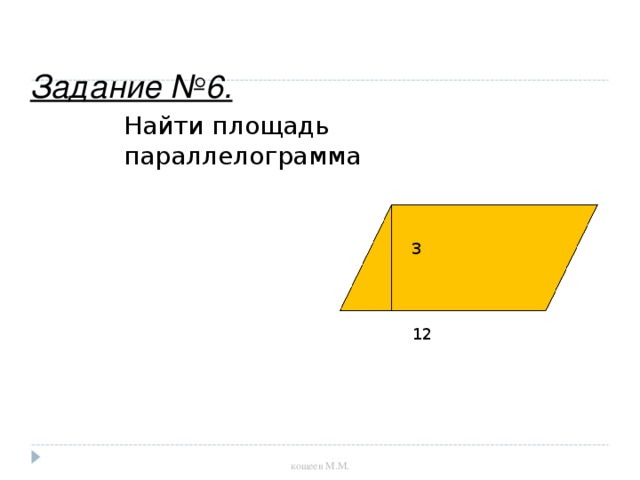
Задание №6.

Найти площадь

параллелограмма

кощеев М.М.

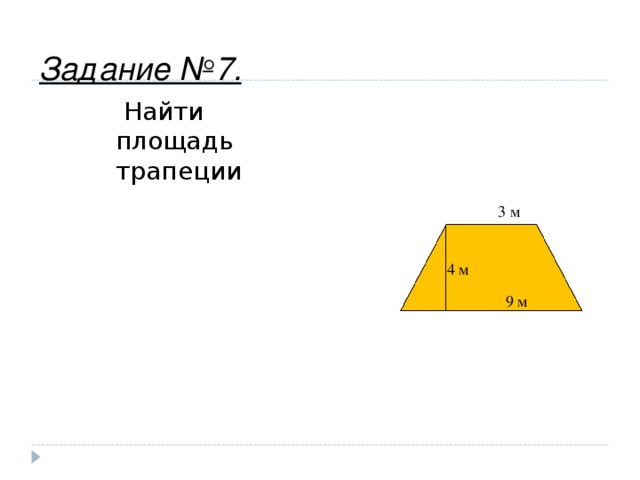
Задание №7.

Найти

площадь

трапеции

3 м

4 м

9 м

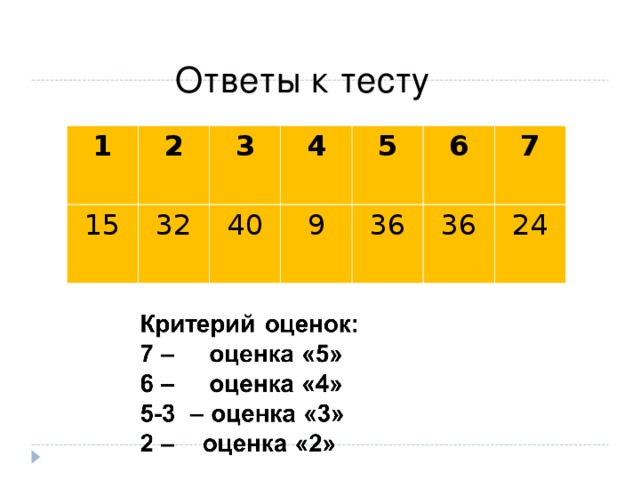
Ответы к тесту

Дидактический материал по геометрии на тему «Площадь фигур» составлен для  отработки
навыков применения формул вычисления площадей треугольников с помощью высоты и основания,
катетов; площадей параллелограмма с помощью основания и высоты; площадей ромба с помощью
диагоналей, высоты и основания; площадей трапеции по средней линии и высоте, основаниям и
высоте.
Разработка содержит двадцать фигур, размещенных на листе в клетку.
Задача учащихся для работы с формулой выполнить необходимые подсчёты по
клеточкам требуемых элементов треугольника или четырехугольника и вычислить площадь каждой
фигуры.
Данная разработка будет полезна и учащимся 9 классов для подготовки к ОГЭ.
Дата
  Фамилия Имя
      Класс
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
№ 1
S Вычислить площадь каждой фигуры, выполнив необходимые измерения по клеточкам
3
4
8
9
1
5
13
15
2
6
10
7
11
16
1
1
1
12
14
2

Источник

Задание 3. ЕГЭ. Найти площадь ромба

Просмотр содержимого документа «Проверочная работа по теме «Площадь» в формате ОГЭ (9 класс)»

Просмотр содержимого документа

«Проверочная работа по теме «Площадь» в формате ОГЭ (9 класс)»