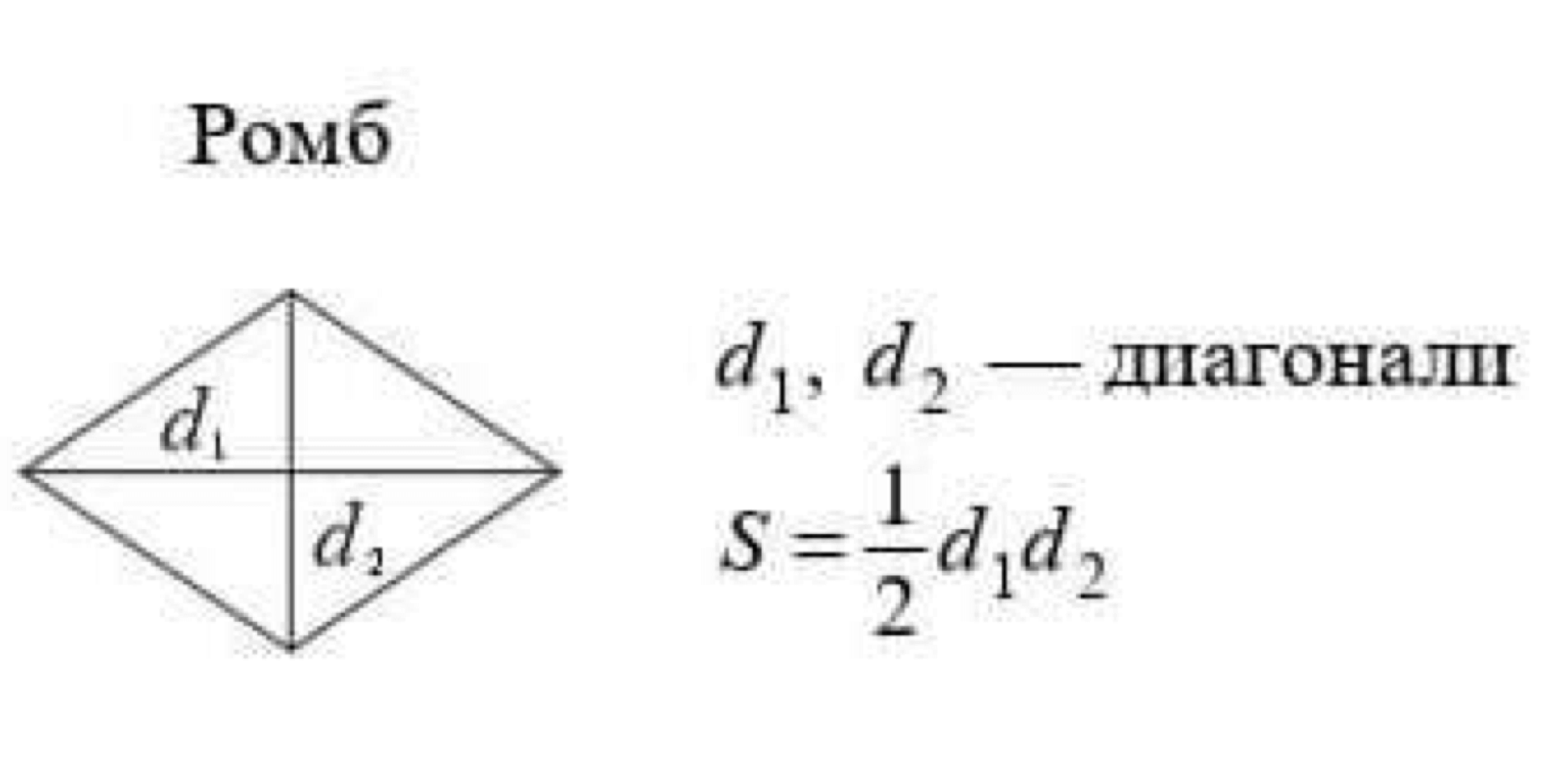Чтобы успешно сдать ОГЭ нужно знать всего три способа как найти площадь ромба. И какой способ применить зависит от того, что вам дано в задаче.
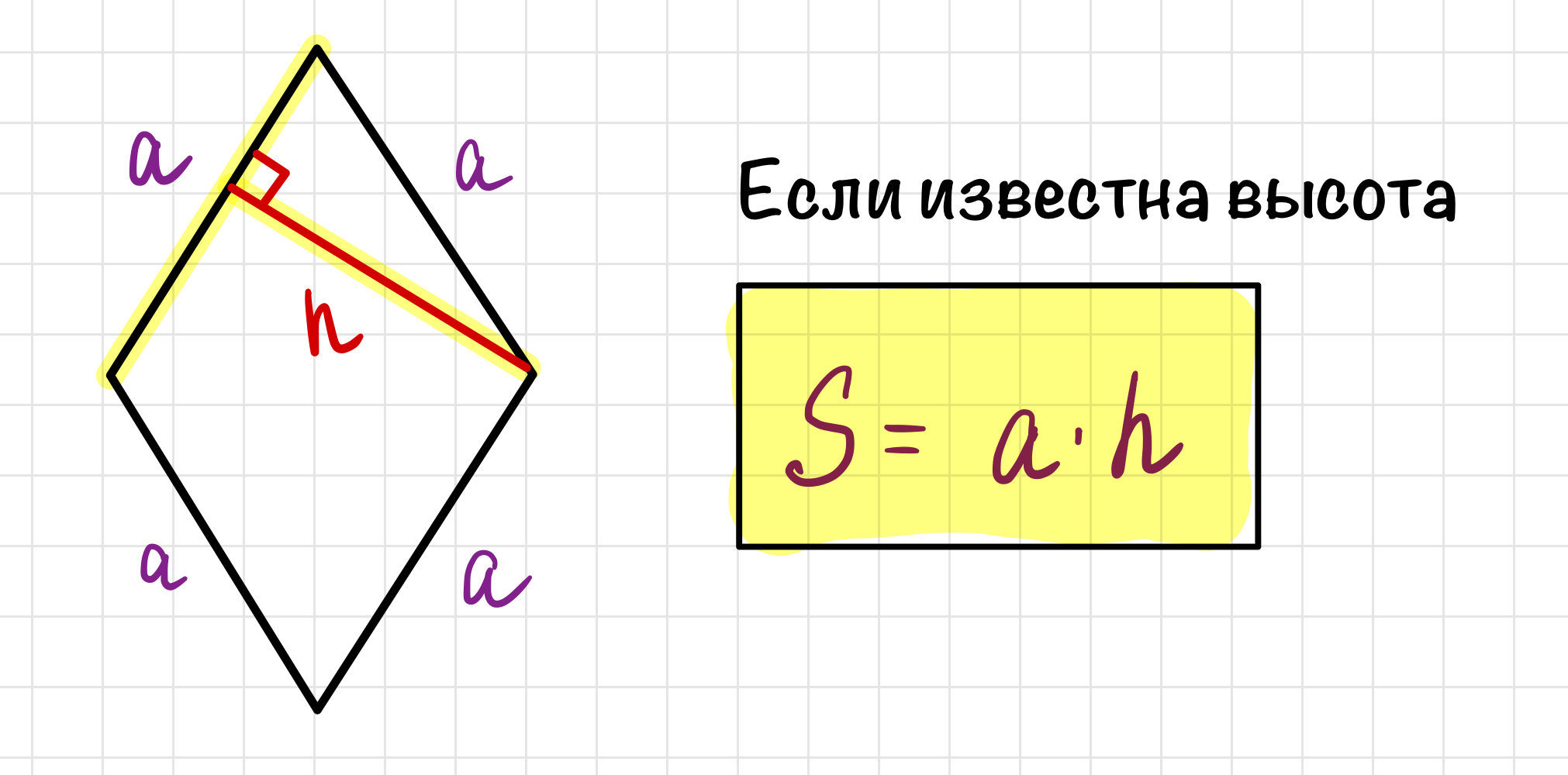
Площадь ромба через высоту
Так как ромб — это параллелограмм, то и его площадь можно найти как прощадь параллелограмма, т.е. умножить высоту на сторону ромба. Кстати, посмотрим где у ромба высота.
Иногда в задаче дана половина площади ромба.
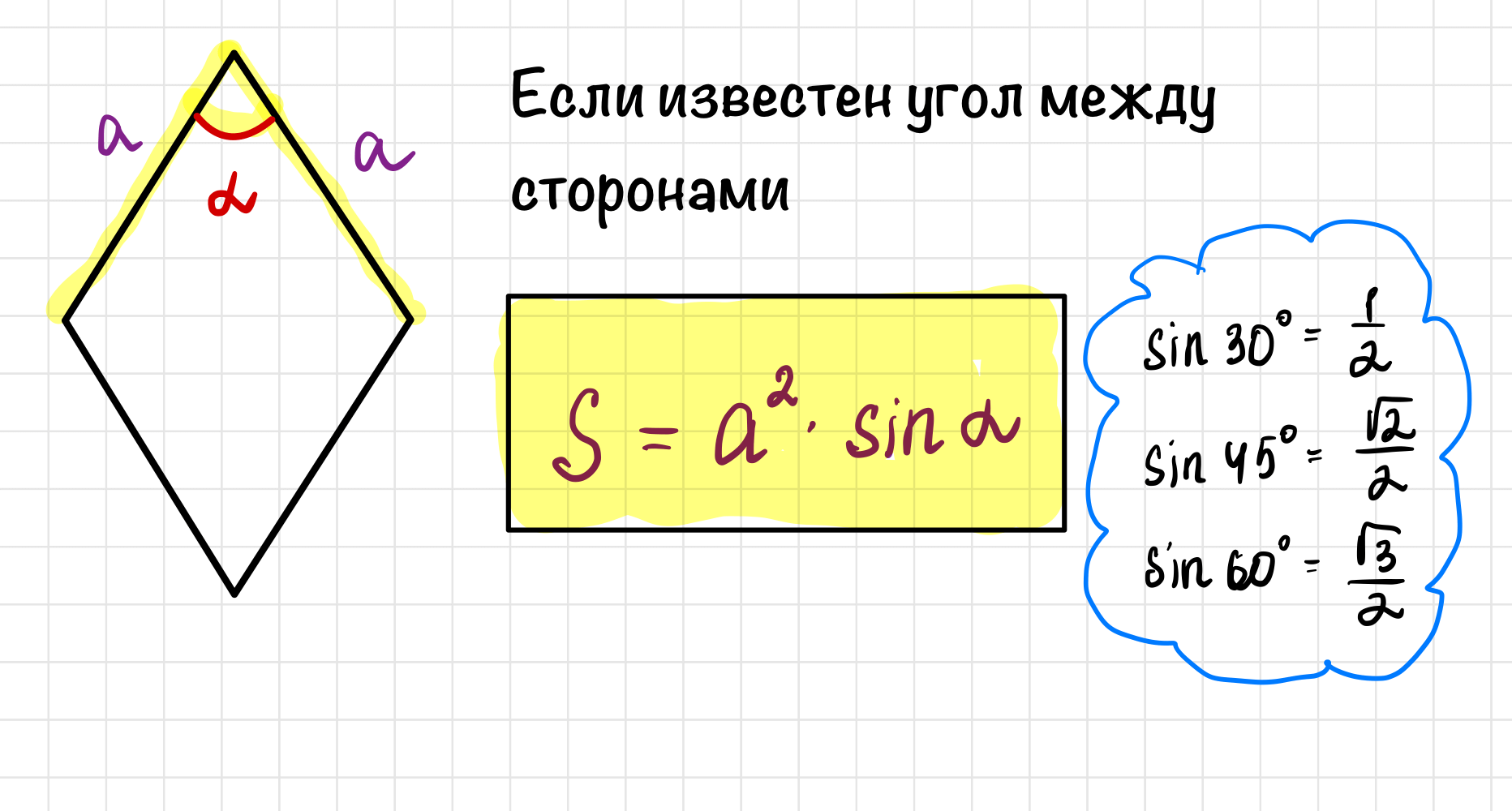
Площадь ромба через сторону и угол
Если в задаче дана сторона ромба и какой-то из его углов, то площадь ромба находим по формуле.
Если дан больший угол ромба и синус такого угла мы не знаем, то сначала находим меньший угол ромба.
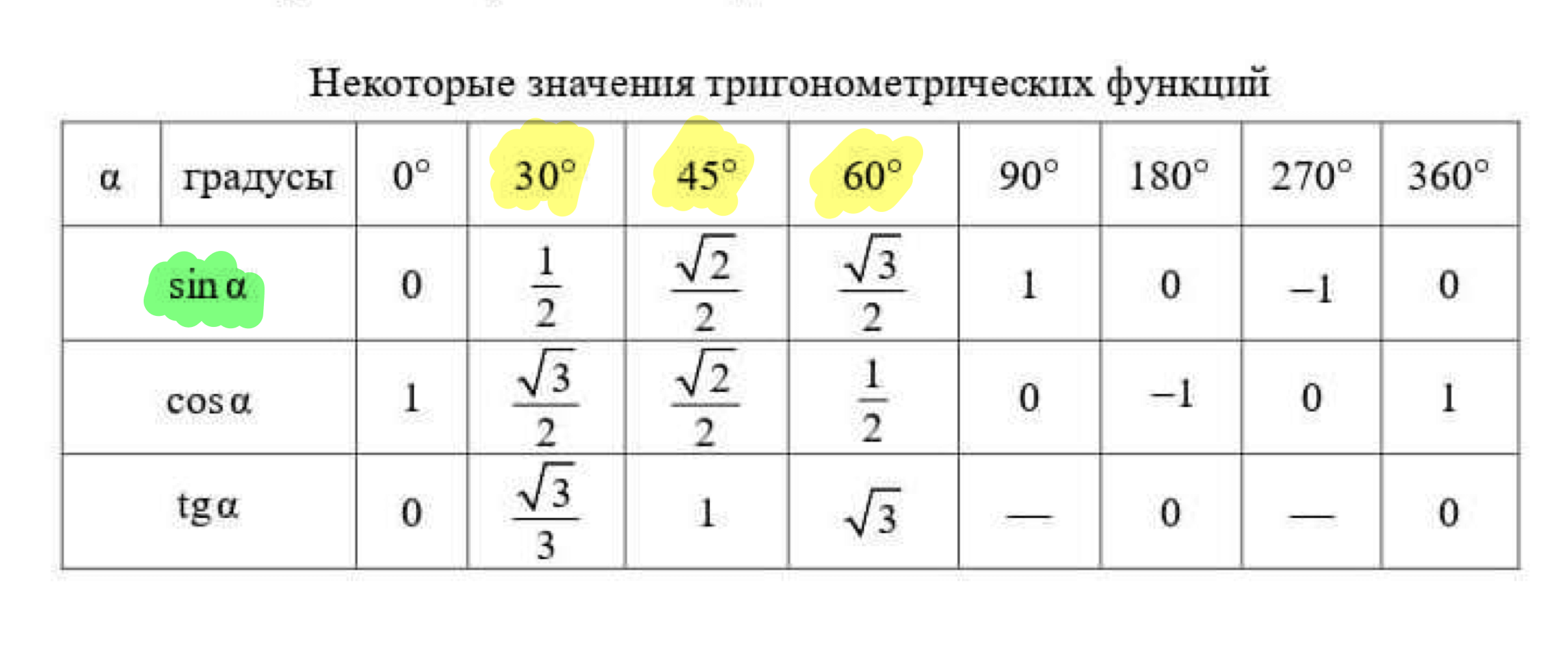
Кстати синусы углов смотрим в раздаточных материалах, если что вы должны знать синусы только трех углов.
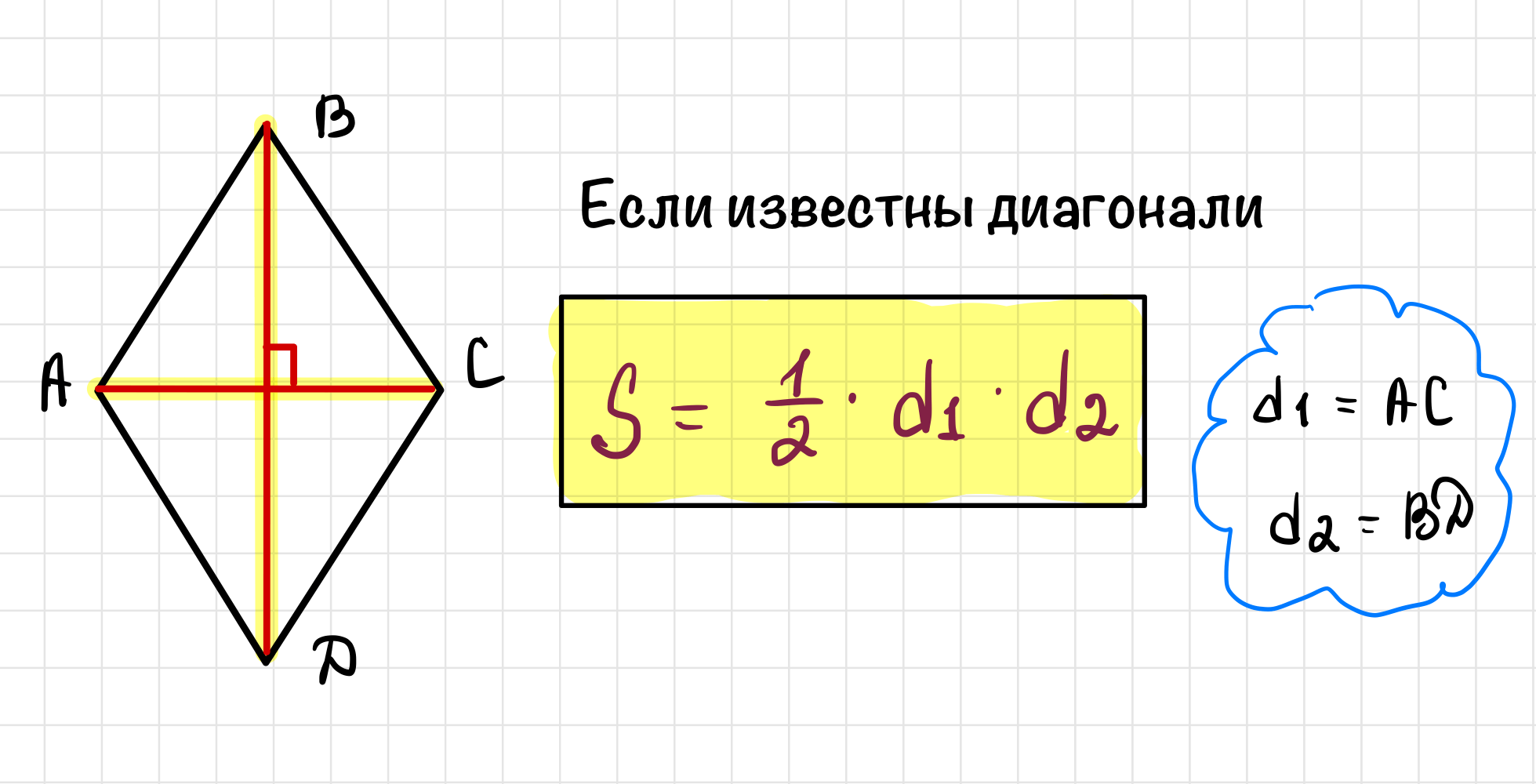
Площадь ромба через диагонали
Пожалуй, эту формулы ОГЭ любит больше всего! Площадь ромба равна половине произведения его диагоналей.
Например:
И эта формула есть в раздаточных материалах!
Всего: 57 1–20 | 21–40 | 41–57
Добавить в вариант
Найдите площадь ромба, если его диагонали равны 10 и 6.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 56.
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Источник: Банк заданий ФИПИ
Периметр ромба равен 24, а один из углов равен 30°. Найдите площадь ромба.
Периметр ромба равен 28, а один из углов равен 30°. Найдите площадь ромба.
Периметр ромба равен 48, а один из углов равен 30°. Найдите площадь ромба.
Периметр ромба равен 60, а один из углов равен 30°. Найдите площадь ромба.
Периметр ромба равен 36, а один из углов равен 30°. Найдите площадь ромба.
Всего: 57 1–20 | 21–40 | 41–57
Образовательный сайт vpr-klass.com (впр-класс.ком) — готовые решения задач!
У нас вы найдете много учебных материалов: решебники, ГДЗ, тестовые задания, видео уроки, генераторы задач, решения упражнений гиа и егэ.
Расскажи друзьям
Ищи САЙТ в Яндексе и Google по слову:
vpr-klass или впр-класс
Сохрани сайт в закладки — нажми Ctrl+D
|
Версия для печати Задача по геометрии решается очень просто, главное знать формулу площади ромба. Площадь ромба равна половине произведения диагоналей ромба. Т.е. одна диагональ равна 6+6=12, а вторая 2,5+2,5=5. Следовательно, площадь равна (12*5)/2=30. Решение: Скачать решение. |
|
Категория: Учебные материалы, Задания ГИА ОГЭ по математике 2017 — решение, подг | |
|
Оставь свой комментарий! |
Интересно
ГИА (ОГЭ) по математике
Много разных решений
Тесты ГИА онлайн.
Видео — ГИА 2013: геометрия
Видео — ГИА 2012
Видео — Демо-вариант 2012.
Решение Демо-варианта 2013 года (2014 года).
Задача №1, Вычислить.
Задача №2, Числа и прямая.
Задача №3, Сравнение чисел.
Задача №4, Уравнения.
Задача №5, Графики и формулы.
Задача №6, Прогрессии.
Задача №7, Упростить выражение.
Задача №8, Неравенства, системы неравенств.
Задача №9, Задания по геометрии.
Генератор вариантов ГИА 2014
ЕГЭ по математике
Много разных решений.
Онлайн тесты.
Видео уроки ЕГЭ по математике.
Генератор вариантов ЕГЭ 2014
Книги, справочники
Решение демо варианта ЕГЭ по математике 2014
Задания B1, задача.
Задания B2, диаграммы.
Задания B5, уравнения.
Задания B8, производная.
Задания B10, вероятность.
ОГЭ по информатике
Видео уроки
Copyright © 2017 vpr-klass.com | Если какой-либо из материалов нарушает ваши авторские права, просим немедленно связаться с Администрацией!!! Наш e-mail: [email protected] | Правообладателям |
sitemap.xml
В данном тесте представлены основные типы задач на использование формул периметра и площади ромба. Они предназначены для итогового повторения курса геометрии по теме «Ромб» как при подготовке к основному государственному экзамену по математике первой части модуля «Геометрия», так и для самостоятельного решения.
Тест по геометрии для подготовки к ОГЭ по теме: «Периметр и площадь ромба» (9 класс)
-
Найдите площадь ромба, если его диагонали равны 8 и 16.
а)24 б)64 в)48 г)128
-
Найдите сторону ромба, если его площадь равна 96, а одна из диагоналей – 12.
а)8 б)16 в)10 г)20
-
Найдите площадь ромба, если его периметр равен 40, а высота – 8.
а)40 б)80 в)320 г)320
-
Найдите площадь ромба, если его высота равна 12, а острый угол 300.
а)288 б)360 в)144 г)72
-
Найдите площадь ромба, если его высота равна 6, а тупой угол 1500.
а)36 б)72 в)18 г)24
-
Найдите площадь ромба, если его сторона равна , а острый угол 450.
а)25 б) в) г)5
-
Найдите площадь ромба, если его сторона равна 5, а острый угол 300.
а) 25 б)12,5 в)20 г)
-
Найдите площадь ромба, если его сторона равна 8, а тупой угол равен 1500.
а)32 б)64 в)36 г)
-
Периметр ромба равен 36, а площадь равна 72. Найдите высоту ромба.
а)9 б)8 в)2 г)4
-
Площадь ромба равна 22,5. Одна из его диагоналей в 5 раз больше другой. Найдите меньшую диагональ.
а)15 б)4,5 в)45 г)3
-
Площадь ромба равна 14. Одна из его диагоналей в 7 раз меньше другой. Найдите большую диагональ.
а)14 б)2 в)4 г)98
-
Площадь ромба равна 24. Одна из его диагоналей на 2 больше другой. Найдите меньшую диагональ.
а)12 б)10 в)22 г)6
-
Площадь ромба равна 40. Одна из его диагоналей составляет 0,8 от другой. Найдите меньшую диагональ.
а)10 б) 8 в)5 г)20
-
Площадь ромба равна 54. Отношение диагоналей равно 3:4. Найдите большую диагональ.
а)9 б)10 в)12 г)7
-
Площадь ромба равна 50, периметр равен 40. Найдите градусную меру острого угла ромба.
а)450 б)600 в)300 г)250
-
Площадь ромба равна 32, периметр равен 32. Найдите градусную меру тупого угла ромба.
а)1500 б)1200 в)1350 г)1000
-
Площадь ромба равна . Периметр равен 24. Найдите градусную меру острого угла ромба.
а)900 б)300 в)600 г)450
-
Площадь ромба равна . Периметр равен 48. Найдите градусную меру тупого угла ромба.
а)1200 б)1350 в)1500 г) 1600
-
Найдите сторону ромба, площадь которого равна площади прямоугольника со сторонами 9 и , а острый угол равен 600.
а)12 б)24 в) г)
-
Найдите площадь ромба, периметр которого равен периметру прямоугольника со сторонами 10 и 18, а тупой угол равен 1200.
а)180 б)14 в) г)
Краткое описание документа:
В данном тесте представлены основные типы задач на использование формул периметра и площади ромба. Они предназначены для итогового повторения курса геометрии по теме «Ромб» как при подготовке к основному государственному экзамену по математике первой части модуля «Геометрия», так и для самостоятельного решения.
Общая информация
Обязательно поделитесь с друзьями:
Скачать
Размер презентации: 22.29 Kb
Нам необходимо рассмотреть все формулы для нахождения площади ромба.
Ромб
Рассмотрим, что в геометрии называется ромбом.
Ромбом в геометрии называется параллелограмм у которого все стороны имеют одинаковую длину.
Параллелограмм называется ромбом тогда, когда выполняются следующие из условий:
- две смежные стороны параллелограмма равны, то есть имеют одинаковую длину. Следовательно все его стороны равны;
- диагонали данной плоской фигуры перпендикулярны, то есть пересекаются под прямым углом;
- диагонали делят углы на две равные части, то есть являются биссектрисами.
Рассмотрим формулы для нахождения площади ромба
Пусть мы имеем ромб обозначенный как abcd в котором ac и bd являются диагоналями данной фигуры.
Рассмотрим формулы нахождения площади:
1.
Одна из наиболее распространенных формул для нахождения площади ромба является формула в которой площадь находится как половина произведения длин его диагоналей. То есть данная формула будет иметь следующий вид:
S = (ac * bd) / 2
2.
Также мы знаем, что площадь ромба можно вычислить исходя из формулы:
S = ab2 * sin a
То есть как произведение квадрата длины стороны на синус прилежащего угла.
3.
Так ромб является параллелограммом следовательно его площадь можно вычислить как произведение длины стороны на высоту h. Данная формула будет иметь вид:
S = ab * h
4.
Зная радиус вписанной окружности и угол между смежными сторонами площадь ромба находится как:
S = 4 * r2 / sin a
5.
Также через радиус вписанной вписанной окружности и длину стороны ромба:
S = 2 * a * r
Английский язык
Астрономия
Белорусский язык
Биология
География
ИЗО
Информатика
История
Итальянский язык
Краеведение
Литература
Математика
Музыка
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
ОРКСЭ
Русский язык
Технология
Физика
Физкультура
Химия
Черчение
Для учителей
Дошкольникам
VIP — доступ
- Предметы
- Математика
- 9 класс
- Площади фигур
»
»
»
Площади фигур
Данный тест подготовлен для подготовки учащихся 9 класса к ОГЭ для закрепления и проверки темы по геометрии «Площади фигур».
Математика 9 класс | Автор: Федукович Н.И. | ID: 7272 | Дата: 27.1.2016
+2
0
Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться
Вопрос №
1
Сторона квадрата равна 21. Найдите площадь квадрата.
Введите ответ:
Вопрос №
2
В прямоугольнике одна сторона равна 20, другая сторона 24. Найдите площадь прямоугольника.
Введите ответ:
Вопрос №
3
Одна из сторон параллелогграмма 31, а опущенная на неё высота равна 7 . Найти площадь параллелограмма.
Введите ответ:
Вопрос №
4
Найдите площадь ромба, если его диагогали равны 8 и 12.
Введите ответ:
Вопрос №
5
Найти высоту ромба. если его площадь равна 54, а сторона равна 4
Введите ответ:
Вопрос №
6
Найдите площадь прямоугольного треугольника, катет которого равен 7, а острый угол 45 градусов
Введите ответ:
Вопрос №
7
Основания трапеции 17 и 22, площадь равна 390. Найдите высоту трапеции
Введите ответ:
Показать ответы
Получение сертификата
о прохождении теста
Доступно только зарегистрированным пользователям
Создайте Ваш сайт учителя
Курсы ПК и ППК
Видеоуроки
Олимпиады
Вебинары для учителей
- Главная
- Математика
- Тесты
- Проверочная работа по теме «Площадь» в формате ОГЭ (9 класс)
Проверочная работа по теме «Площадь» в формате ОГЭ для 9 класса. Содержит 5 заданий: 1) выбрать верное утверждение; 2) найти площадь фигуры, изображенной на рисунке; 3-5 текстовые задачи на нахождение площади плоских фигур.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Проверочная работа по теме «Площадь» в формате ОГЭ (9 класс)»
Предмет: Математика
Категория: Тесты
Целевая
аудитория: 9 класс.
Урок соответствует ФГОС
Автор: Касьянова Наталья Игоревна
Дата: 12.12.2016
Номер свидетельства: 369009
Учебник
Геометрия, 9 класс
Ромб: Формулы, Площадь, Вписанная Окружность
Ромб — это параллелограмм, у которого все стороны равны.
- «Чтоб Выучить, распознать нечто стоящее — узнать его в движении, при изменениях»
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей — ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали — новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали — ромб совпадает с самим собой. Симметрия.
Замечание: Если «зряче видим» центральную и осевые симметрии ромба, то все его свойства у нас «в кармане».
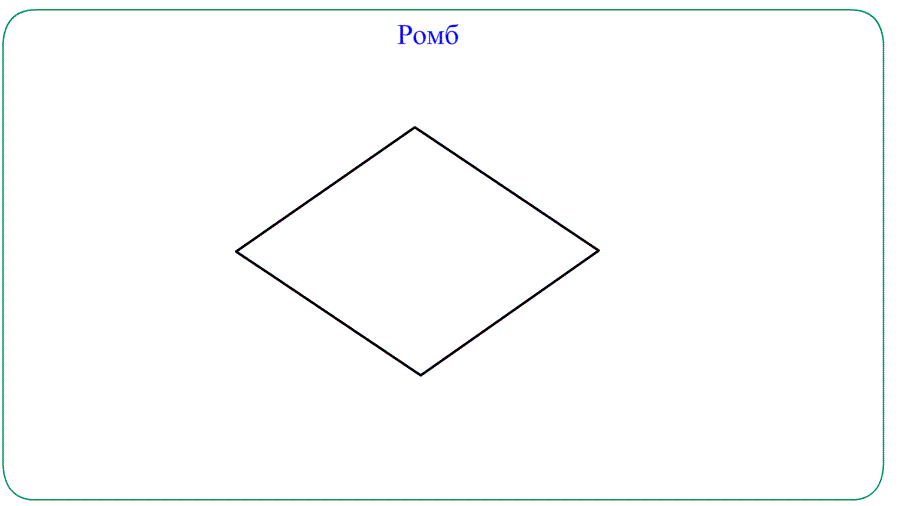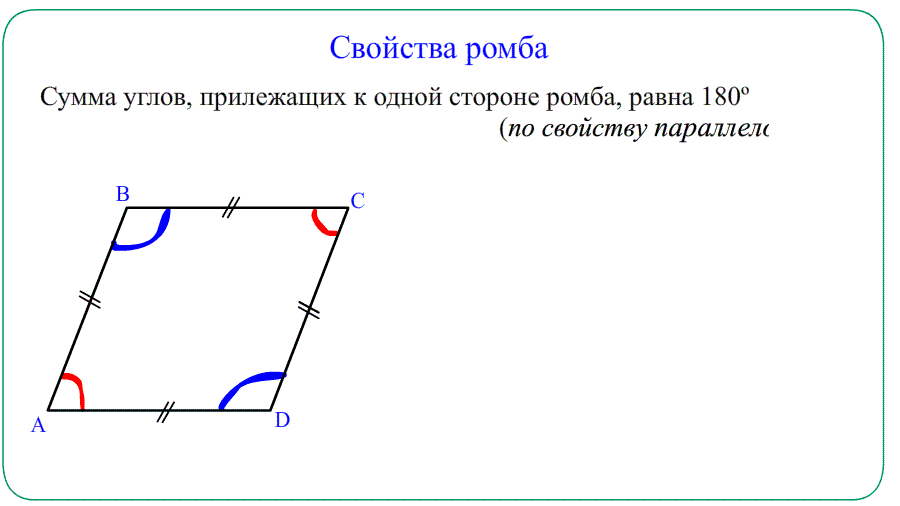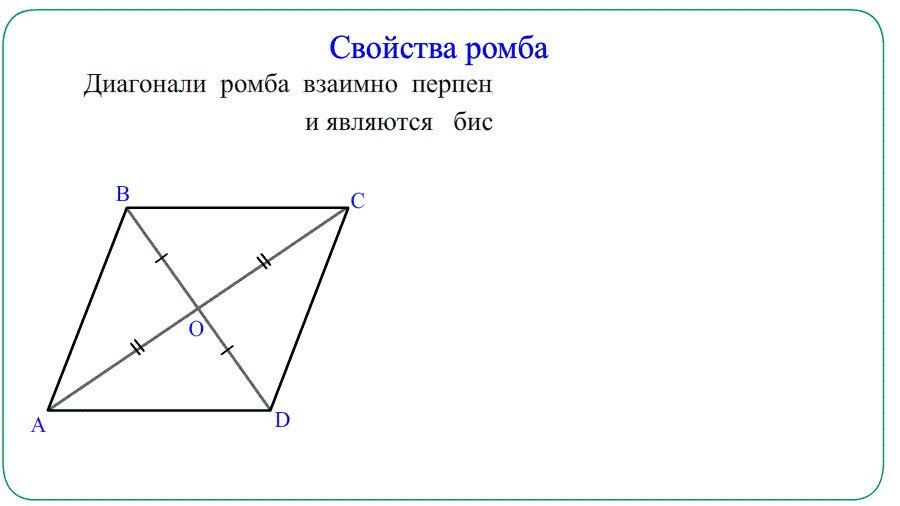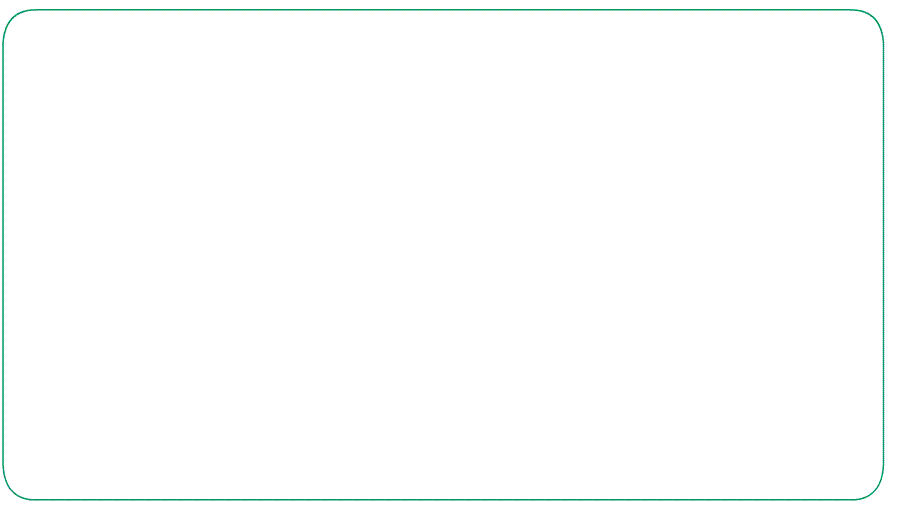
Свойства ромба:
- Ромб симметричен относительно точки O — пересечения диагоналей. O — центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ — ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов — делят углы пополам.
- Диагонали ромба со сторанами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2cdot acdot bcdotcos D$ , большая — $BD^2=a^2+b^2+2cdot acdot bcdotcos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Формулы Площади ромба:
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=ADcdot CH$ , $S=acdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2cdotsin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=frac{ACcdot BD}{2}$ . — половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если … суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=pcdot r$, $p=2cdot a$ $S=2cdot a cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали — суть биссектрисы углов.
Задача 1: Найти периметр ромба $ABCD$, в котором $angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков данный треугольник?
- По условию, угол $bigtriangleup BCD$ у вершине $angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: «Односторонние углы»: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


Задача 3: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $alpha$ в $bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $Rightarrow$ $sinalpha=frac{BE}{BD}=frac{12}{13}$
- Перейдем к $bigtriangleup OCD$ : в нем прилежащий катет $OD=frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $sin^2alpha+cos^2alpha=1$ . Тогда косинус: $cosalpha=pmsqrt{1-sin^2alpha}=pmsqrt{1-frac{144}{169}}=pmsqrt{frac{25}{169}}=pmfrac{5}{13}$
- Угол $alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $cosalpha = frac{5}{13}$
- Тогда: $frac{DO}{DC}=frac{6,5}{DC}=cosalpha=frac{5}{13}$ $Rightarrow$ $DC=frac{6,5cdot13}{5}=frac{13cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9cdot12=202,8$
Задача 4: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ — пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.
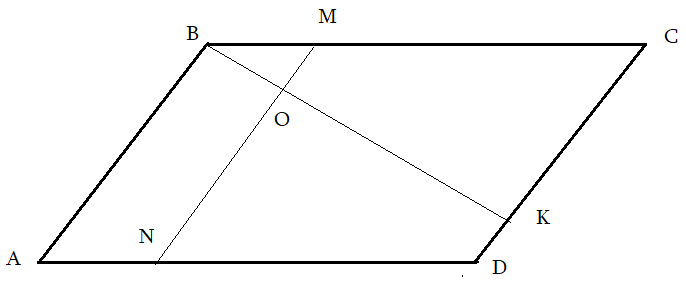
Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ — параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ — квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
Ромб — это параллелограмм, у которого все стороны равны.
- «Чтоб Выучить, распознать нечто неподвижное — узнать его в движении, при изменениях»
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей — ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали — новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали — ромб совпадает с самим собой. Симметрия.
Замечание: Если «зряче видим» центральную и осевые симметрии ромба, то все его свойства у нас «в кармане».
Свойства ромба:
- Ромб симметричен относительно точки O — пересечения диагоналей. O — центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ — ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов — делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Квадрат — одновременно прямоугольник, ромб, параллелограмм. Диагонали квадрата равны между собой и делятся пополам.
Задача 1: Найти периметр ромба $ABCD$, в котором $angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков данный треугольник?
- По условию, угол $bigtriangleup BCD$ у вершины $angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: «Односторонние углы»: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


- Полезные напоминания: «В равностороннем треугольнике все углы равны 60 градусов.
- Если в равнобренном треугольнике один из углов 60, то это равносторонный треугольник — стороны равны, углы тоже.
- В прямоугольном треугольнике катет напротив угла 30 градусов равен половине гипотенузы.
Упражнения:
Задачи из сайта https://resh.edu.ru :
Задача 11: В ромбе АВСD ∠А = 140°, диагонали пересекаются в точке O. Найдите угол CBO.
Задача 12: В ромбе ABCD ∠С = 50°. Точка O – точка пересечения диагоналей ромба. Найдите угол OBC.
Задача 13: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Задача 14: ???? В любом ромбе равны… Противолежащие углы равны, сумма соседних углов равна 180 градусов:(?) Ромб, у которого все углы равны, это… (?) Диагонали пересекаются и точкой пересечения делятся пополам. (?) Диагонали взаимно перпендикулярны. (?)
Задача 15: Отрезки AB и CD пересекаются в их общей середине. В образовавшемся четырёхугольнике ∠CAD = ∠ADB. Найдите ∠BCA.
Задача 16: На диагонали квадрата как на стороне построен новый квадрат. Чему равна его диагональ, если сторона исходного квадрата равна 6 см?
Задача 17: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Ромб – это геометрическая фигура; параллелограмм, имеющие 4 равные стороны.
-
Формула вычисления площади
- По длине стороны и высоте
- По длине стороны и углу
- По длинам диагоналей
- Примеры задач
Формула вычисления площади
По длине стороны и высоте
Площадь ромба (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a ⋅ h
По длине стороны и углу
Площадь ромба равняется произведению квадрата длины его стороны и синуса угла между сторонами:
S = a 2 ⋅ sin α
По длинам диагоналей
Площадь ромба равна одной второй произведения его диагоналей.
S = 1/2 ⋅ d1 ⋅ d2
Примеры задач
Задание 1
Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.
Решение:
Используем первую формулу, рассмотренную выше: S = 10 см ⋅ 8 см = 80 см2.
Задание 2
Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.
Решение:
Применим вторую формулу, в которой используются известные по условиям задания величины: S = (6 см)2 ⋅ sin 30° = 36 см2 ⋅ 1/2 = 18 см2.
Задание 3
Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.
Решение:
Воспользуемся третьей формулой, в которой используются длины диагоналей: S = 1/2 ⋅ 4 см ⋅ 8 см = 16 см2.