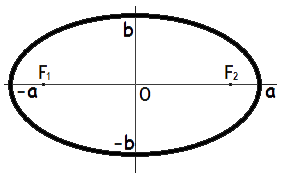Как найти площадь ромба прямоугольного треугольника

Все формулы по геометрии. Площади фигур

Чтобы решать задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.

Начнем с квадрата.

Площадь квадрата равна квадрату его стороны.

Площадь прямоугольника равна произведению его длины и ширины.

Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне. Она также равна произведению его сторон на синус угла между ними.

Для площади треугольника есть целых 5 формул. И все они применяются в задачах ЕГЭ.

1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:

2) Она также равна половине произведения его сторон на синус угла между ними:

3) По формуле Герона, где полупериметр.

4) Также площадь треугольника равна произведению его полупериметра на радис вписанной окружности, S = pr.

5) Еще один способ. Площадь треугольника равна произведению его сторон, деленному на 4 радиуса описанной окружности,

Есть и другие формулы для площади треугольника. Но для решения заданий ЕГЭ, и первой, и второй части, достаточно этих пяти.

Площадь прямоугольного треугольника равна половине произведения его катетов. Она также равна половине произведения гипотенузы на высоту, проведенную к этой гипотенузе:

Площадь правильного треугольника равна квадрату его стороны, умноженному на и деленному на 4:

Площадь трапеции равна произведению полусуммы оснований на высоту,

Также можно сказать, что площадь трапеции равна произведению ее средней линии на высоту,

Площадь произвольного четырехугольника равна половине произведения его диагоналей на синус угла между ними,

Площадь ромба равна произведению квадрата его стороны на синус угла ромба. Она также равна половине произведения диагоналей:

Площадь круга равна произведению числа и квадрата радиуса круга.

Ее также можно записать как произведение числа и квадрата диаметра круга, деленного на 4:

Вспомним важные свойства площадей фигур.

1. Равные фигуры имеют равные площади.
   Иногда фигуры, имеющие равные площади, еще называют равновеликими.
2. Если фигура составлена из нескольких фигур, не имеющих общих внутренних точек, то ее площадь равна сумме площадей этих фигур.

Пример. Найдем площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1см1см.

Решение:

Найдем площадь фигуры на рисунке как сумму площадей нескольких фигур.

На рисунке это три треугольника и трапеция, указаны их площади. Тогда площадь фигуры равна 10 + 3,5 + 1,5 + 3 = 18.

Ответ: 18.

3. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Треугольники АВС и на рисунке называются подобными.

У треугольника все стороны в k раз длиннее, чем у треугольника АВС. Высота треугольника в k раз длиннее, чем высота треугольника АВС. Тогда площадь треугольника в раз больше, чем площадь треугольника АВС.

4. На рисунке показаны треугольники АВС и BCD, имеющие общую высоту. Отношение площадей этих треугольников равно отношению АС к CD:

5. Треугольники АВС и АЕС на рисунке имеют одинаковое основание и разные высоты.

Отношение площадей этих треугольников равно отношению их высот:

6. Медиана треугольника делит его на два равновеликих, то есть равных по площади, треугольника.

На рисунке СМ — медиана треугольника АВС. Площади треугольников АСМ и ВСМ равны.

7. Три медианы треугольника делят его на шесть равных по площади треугольников.

На рисунке все 6 треугольников, из которых состоит треугольник АВС, имеют равные лощади.

Задачи ЕГЭ и ОГЭ по теме: Площади фигур.

Задача 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен

Решение:

Площадь треугольника равна половине произведения его сторон на синус угла между ними. Поэтому

Ответ: 24.

Задача 2. Площадь треугольника ABC равна 4, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.

Решение:

Так как DE и АВ параллельны, треугольники CDE и САВ подобны с коэффициентом подобия Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда

Ответ: 1.

Задача 3. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?

Решение:

Выразим площадь двумя способами:

Тогда

Ответ: 6.

Задача 4. Площадь треугольника ABC равна 10, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.

Решение:

Треугольник CDE подобен треугольнику CAB с коэффициентом Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому

Следовательно, .

Ответ: 7,5.

Задача 5. В параллелограмме ABCD AB = 3, AD = 21, . Найдите большую высоту параллелограмма.

Решение:

Большая высота — это DH, потому что проведена к меньшей стороне. Из треугольника АDН:

Ответ: 18.

Задача 6. Найдите площадь квадрата, если его диагональ равна 1.

Решение:

Квадрат — это частный случай ромба. Площадь квадрата равна половине произведения его диагоналей. Поэтому она равна 0,5.

Ответ: 0,5.

Задача 7. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.

Решение:

Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Площадь прямоугольника равна тогда одна из сторон равна 3, а другая 6. Периметр P = 2 · 3 + 2 · 6 = 18.

Ответ: 18.

Задача 8. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Решение:

Площадь параллелограмма равна произведению его сторон на синус угла между ними. Площадь прямоугольника равна произведению длины на ширину. Пусть одна сторона параллелограмма и прямоугольника равна вторая равна а острый угол параллелограмма равен Тогда площадь параллелограмма равна а площадь прямоугольника равна

По условию площадь прямоугольника вдвое больше:

Следовательно,

Ответ: 30.

Задача 9. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Решение:

Площадь параллелограмма равна произведению его основания на высоту, проведенную к этому основанию. Пусть высоты равны соответственно a и b. Тогда S = 5 · a = 10 · b = 40. Поэтому a = 8, b = 4. Большая высота равна 8.

Ответ: 8.

Задача 10. Найдите площадь ромба, если его высота равна 2, а острый угол 30

Решение:

Площадь ромба равна произведению квадрата его стороны на синус угла ромба. С другой стороны, площадь ромба равна произведению его основания на высоту, проведенную к этому основанию. Пусть сторона ромба равна

Получим уравнение:

Корень уравнения a = 4, поэтому

Ответ: 8.

Задача 11. Найдите площадь ромба, если его диагонали равны 4 и 12.

Решение:

Площадь ромба равна половине произведения его диагоналей.

Ответ: 24.

Задача 12. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

Решение:

Трапеция равнобедренная, значит,

Тогда по теореме Пифагора из треугольника ADH:

Ответ: 160.

Задача 13. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45

Решение:

Проведем высоту CH. Треугольник CHB — прямоугольный, в нем

значит, он также равнобедренный, CH = HB = 4.

Ответ: 16.

Задача 14. Высота трапеции равна 5, площадь равна 75. Найдите среднюю линию трапеции.

Решение:

Средняя линия трапеции равна полусумме оснований. Выразим её из формулы площади трапеции:

Ответ: 15.

Задача 15. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту. Пусть высота равна h, тогда

Из этого уравнения получим: h = 4.

Рассмотрим прямоугольный треугольник, гипотенузой которого является боковая сторона трапеции, равная 8, а катетом — высота трапеции. Длина катета равна половине гипотенузы, следовательно, он лежит напротив угла

Ответ: 30.

Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Задача 16. Найдем площадь четырехугольника на рисунке.

Решение:

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным 5. Высоты этих треугольников равны 2 и 3. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:

Ответ: 12,5.

В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Задача 17. Найдем площадь треугольника, изображенного на клетчатой бумаге.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной 5 и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:

Ответ: 10,5.

Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.

Задача 18.

Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.

Решение:

На этом рисунке мы видим часть круга. Площадь всего круга равна так как Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R = 1), а длина дуги данного сектора равна 2, следовательно, длина дуги в  раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в  раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в  раз меньше, чем площадь всего круга.

Ответ: 1.

Формула Пика

Покажем, как вычислять площадь фигуры, изображенной на координатной плоскости, с помощью формулы Пика.

Задача 19. Найдите площадь многоугольника АВСDE, изображенного на рисунке.

Первый способ:

Площадь многоугольника ABCDE равна сумме площадей треугольника BCD, трапеции BKDE и треугольника AKE.

Имеем:

Второй способ — применить формулу Пика.

Назовем точку координатной плоскости целочисленной, если обе ее координаты — целые числа. На нашем рисунке это точки на пересечениях линий, разделяющих клетчатую бумагу на клетки.

Площадь многоугольника с целочисленными вершинами равна

.

Здесь В — количество целочисленных точек внутри многоугольника, Г — количество целочисленных точек на границе многоугольника.

Главное — аккуратно посчитать. На нашем рисунке

В = 24 (показаны зеленым),

Г = 8 (показаны красным),

S = 24 + — 1 = 27.

Ответ: 27.

Формулы площади треугольника

1. Формула площади треугольника по стороне и высоте
   Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
2. Формула площади треугольника по трем сторонам 
   

   Формула Герона

   S = √

   p

   (

   p — a

   )(

   p — b

   )(

   p — c

   )

3. Формула площади треугольника по двум сторонам и углу между ними 
   Площадь треугольника равна половине произведения двух его сторон, умноженного на синус угла между ними.
4. Формула площади треугольника по трем сторонам и радиусу описанной окружности
5. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
   Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S — площадь треугольника,

a, b, c

 — длины сторон треугольника,

h

 — высота треугольника,

γ

 — угол между сторонами 

a

 и 

b

,

r

 — радиус вписанной окружности,
R — радиус описанной окружности,

p  =	a  +  b  +  c	— полупериметр треугольника.
2

План урока:

Площадь прямоугольного треугольника

Площадь произвольного треугольника

Площадь параллелограмма

Площадь ромба

Площадь трапеции

Площадь прямоугольного треугольника

Пусть в прямоугольном треугольнике известны два его катета. Обозначим их буквами а и b. Как тогда вычислить площадь такого треуг-ка?

Прямоугольный треугольник можно достроить до прямоугольника:

Площадь получившегося прямоугольника равна произведению чисел а и b. С другой стороны, прямоугольник состоит из двух треуг-ков площадью S, поэтому его общая площадь составляет 2S. Тогда можно записать, что

Задание. Катеты прямоугольного треугольника имеют длины 3 и 4. Определите его площадь.

Решение. Просто подставляем в формулу вместе букв a и b числа 3 и 4:

Задание. Площадь прямоугольного треугольника равна 100, а один катет больше другого вдвое. Найдите оба катета.

Решение. Пусть меньший катет равен х, тогда больший катет будет равен 2х. Выразим площадь прямоугольного треугольника через х:

Естественно, нас интересует только положительный корень, а отрицательный можно отбросить:

x = 10

Меньший катет оказался равным 10, тогда больший катет, который вдвое больше, будет равен 20.

Ответ: 10; 20.

Задание. Найдите площадь фигуры, показанной на рисунке. Сторона каждой клеточки имеет длину, равную единице:

Решение. Эту фигуру можно разбить на квадрат со стороной 8 и два прямоугольных треуг-ка, то есть всего на три фигуры:

Подсчитаем площадь каждой из трех фигур по отдельности:

Чтобы найти площадь всей фигуры, достаточно просто сложить три полученных числа:

Задание. Вычислите площадь треуг-ка, изображенного на рисунке (площадь каждой отдельной клеточки составляет единицу):

Решение. Здесь проблема заключается в том, что треуг-к прямоугольным не является. Однако можно построить прямоуг-к, который будет состоять сразу из 4 треуг-ков:

Мы можем найти как площадь всего прямоугольника (обозначим ее как S), так и площади трех прямоугольных треуг-ков S₁, S₂ и S₃:

Площадь произвольного треугольника

Перейдем к более сложному случаю, когда необходимо подсчитать площадь произвольного треугольника, не являющегося прямоугольным. Предположим, надо найти площадь произвольного ∆АВС. Опустим из А на сторону ВС высоту АН:

В результате мы получили два прямоугольных треуг-ка, ∆АВН и ∆АCН. Мы уже знаем, как найти их площади:

Общая площадь всего ∆АВС равна сумме площадей ∆АВН и ∆АСН. Запишем ее и вынесем общий множитель АН/2 за скобки:

В скобках стоит сумма ВН + НС. Но ведь эта сумма равна длине стороны ВС! Тогда окончательно формулу можно записать в виде:

Получили, что для вычисления площади произвольного треугольника надо сначала умножить его высоту на сторону, на которую она падает, а далее поделить результат на 2. Однако для полного доказательства этого факта надо рассмотреть особый случай, когда высота в треуг-ке падает не на сторону, а на ее продолжение (такая ситуация возникает в тупоугольном треуг-ке):

На рисунке снова получились всё те же прямоугольные треуг-ки ∆АСН и ∆АВН. Запишем формулы их площади:

Отличие в том, что на этот раз площадь АВС можно вычислить не как сумму, а как разницу этих площадей:

Итак, можно сформулировать следующее правило:

Примечание. Часто сторону, на которую опущена высота, называют основанием треуг-ка.

Задание. Вычислите площадь ∆АВС, если сторона АВ имеет длину 7, а высота СН равна 4.

Решение. В данной задаче на сторону длиной 7 падает высота длиной 4. Надо просто подставить эти числа в формулу:

Задание. Докажите, что медиана треуг-ка разбивает его на два равновеликих треуг-ка.

Решение.

Пусть в ∆АВС проведена медиана СМ. Требуется доказать, что

Важно заметить, что СН будет являться высотой не только для ∆АВС, но также и для ∆СВМ и ∆САМ. Обозначим СН как h, а АВ как а. Тогда мы можем найти длины отрезков ВМ и АМ, ведь медиана делит сторону АВ пополам:

Получили одно и то же значение, то есть площади треуг-ков равны.

В рассмотренной задаче мы использовали тот факт, что у нескольких треуг-ков может быть общая высота. Общая высота используется и в многих других геометрических задачах.

Задание. Предложите способ, как разделить треуг-к, показанный на рисунке, на три равновеликих треуг-ка:

Чтобы треуг-ки были равновелики, достаточно, чтобы у них была общая высота, а основания, на которые эта высота падает, были бы равны друг другу. Поэтому можно просто поделить нижнюю сторону на три одинаковых отрезка (длиной по 7 клеток) и соединить концы полученных отрезков с противоположной вершиной:

Красной линией здесь показаны границы треуг-ков, а штриховой – их общая высота СН. Вычислить площадь каждого из треуг-ков можно по следующим формулам:

Но отрезки BD, DE и EA одинаковы (по 7 клеточек), поэтому одинаковы будут и площади:

Заметим, что необязательно делить на три одинаковых отрезка именно нижнюю сторону. Допустимы и два других варианта решения:

Но и это не единственные решения задачи. Попробуйте самостоятельно предложить ещё несколько вариантов.

Формула площади треуг-ка показывает, что между длинами высот и сторон есть взаимосвязь.

Задание.В ∆РЕТ РЕ = 72, ЕТ = 45. Высота ТН имеет длину 40. Найдите высоту РМ.

Решение.

Зная ТН и РЕ, мы сможем найти площадь треуг-ка:

Теперь запишем эту формулу площади в ином виде, когда используется высота МР и сторона ЕТ

Величину S_РЕТ мы только что вычислили, а длина ЕТ известна из условия, поэтому можно подставить их в формулу:

Площадь параллелограмма

Для вычисления площади параллелограмма введем понятие «высота параллелограмма». Так называют перпендикуляр, опущенный на сторону параллелограмма (ее в такой ситуации часто называют основанием) из одной из вершин параллелограмма. Важно понимать, что высоты могут упасть не на само основание, а на его продолжение. Так как у каждого параллелограмма есть 4 вершины, а из каждой из них можно опустить высоту на две противоположных вершины, то всего у параллелограмма должно быть 8 высот:

На рисунке синим показаны высоты параллелограмма, а красным цветом отмечены продолжения оснований. Оказывается, что площадь параллелограмма равна произведению его высоты и основания, на которую она опущена. Докажем это.

Опустим в параллелограмме АВСD высоты ВН и СК:

В результате получили четырехуг-к ВНКС, который является прямоугольником, ведь все его углы прямые. Очевидно, что ∆АВН и ∆DCK равные. Это можно доказать тем, что они являются прямоугольными, у них есть одинаковые гипотенузы АВ и CD (они равны как противоположные стороны параллелограмма) и одинаковые катеты ВН и СК (это уже противоположные стороны прямоугольника ВНКС).

Раз они равны, то одинаковы и их площади:

Но величину S₃ можно заменить на S₂. В свою очередь полученная сумма равна площади прямоугольника ВНКС, которая может быть вычислена как произведение его смежных сторон:

Но ВН – это высота, а НК – основание параллелограмма. То есть мы доказали следующее утверждение:

Задание. Найдите площадь параллелограмма, изображенного на рисунке:

Решение. По рисунке несложно определить длину как основания, так и высоты параллелограмма:

Далее надо просто перемножить эти длины:

Примечание. Конечно, если вы вдруг забыли формулу площади параллелограмма, можно просто разделить его на прямоугольник и два прямоугольных треуг-ка:

Дальше можно просто посчитать по отдельности S₁, S₂и S₃, после чего сложить их. Попробуйте сделать это самостоятельно.

Задание. Площадь параллелограмма равна 162 см², а одна из его высот вдвое короче основания, к которому она проведена. Найдите эту высоту и основание.

Решение. В данной задаче не потребуется даже рисунок. Обозначим высоту буквой h, тогда основание, которое вдвое длиннее, составляет 2h. Произведение этих чисел – это площадь, то есть оно равно 162:

Высота равна 9, а основание будет вдвое больше, то есть его длина равна 18.

Ответ: 9 и 18.

Задание. Смежные стороны параллелограмма ABCD имеют длину 12 и 14 см, а угол между ними равен 30°. Вычислите его площадь.

Решение. Опустим на сторону длиной 14 см высоту:

Для вычисления площади надо сначала найти высоту ВН. Её можно определить из ∆АВН. Он является прямоугольным, а его острый угол∠А = 30°. У такого треуг-ка катет, лежащий против 30°, вдвое меньше АВ:

Площадь ромба

Многие четырехуг-ки, изученные нами ранее, являются частными случаями параллелограмма. Для прямоугольника и квадрата мы уже знаем формулы вычисления площади. Осталось разобраться с ромбом. Ясно, что его площадь можно найти также, как и у параллелограмма. Однако площадь ромба можно посчитать и зная только его диагонали.

Построим ромб и проведем в нем диагонали:

Нам уже известно, что диагонали ромба пересекаются под прямым углом, а точка их пересечения является серединой для каждой диагонали:

Получается, что диагонали разбивают ромб на 4 одинаковых прямоугольных треуг-ка. Высчитаем, к примеру, S_AOB:

В результате мы доказали следующее утверждение:

Задание. Одна диагональ ромба равна 3,2 дм, а другая составляет 14 см. Найдите его площадь.

Решение. Для начала надо перевести все длины в одинаковые единицы измерения. Заменим дециметры на сантиметры:

Задание. Одна диагональ ромба в три раза длиннее другой, а площадь фигуры составляет 150. Вычислите длину диагоналей ромба.

Решение. Обозначим меньшую диагональ как х, тогда вторая будет равна 3х. Выразим площадь через х:

Вторая диагональ ромба будет втрое длиннее, то есть ее длина равна 3•10 = 30

Ответ: 10 и 30 см.

Площадь трапеции

Осталось рассмотреть единственный известный нам вид четырехуг-ка, который не является параллелограммом. Это трапеция. Для вычисления ее площади также потребуется высота. Под ней подразумевают перпендикуляр, опущенный из вершины трапеции на одно из ее оснований. Другими словами, высота трапеции – это расстояние между основаниями трапеции.

В произвольной трапеции ABCD, где АD – большее основание, опустим из В высоту (то есть перпендикуляр) на AD, а из D– высоту на ВС. Также проведем диагональ ВD:

Ясно, что общая площадь трапеции будет равна сумме площадей ∆АВDи ∆ВСD. В свою очередь площадь каждого из них можно подсчитать по стороне и опущенной на нее высоте. Высоты мы как раз и провели, это ВН и DK, поэтому можно записать:

Теперь заметим, что отрезки ВН и КD одинаковы, ведь фигура ВНDК является прямоугольником. Тогда площадь ∆ВСD можно записать в таком виде:

В итоге мы доказали, что для вычисления площади трапеции следует ее высоту умножить на сумму длин оснований, после чего поделить результат на два. Обычно этот факт записывают следующим образом:

Задание. У трапеции АВСD основаниями являются АВ (21 см) и CD (17 см). Высота ВН составляет 7 см. Найдите площадь трапеции.

Решение. Это простая задача на использование формулы площади трапеции:

Задание. Найдите площадь прямоугольной трапеции, показанной на рисунке (площадь клеточки равна единице):

Решение. На рисунке показана прямоугольная трапеция. Её высота равна длине ее правой боковой стороны трапеции. Покажем размеры, необходимые нам для выполнения расчета:

Считаем площадь:

Задание. Тупой угол равнобедренной трапеции составляет 135°. Проведенная из этого угла высота делит противолежащее основание на отрезки длиной 14 и 34 см. Какова площадь трапеции?

Решение. Выполним построение:

Найдем острый угол трапеции. Так как CD||АВ, то

Рассмотрим ∆АDH. Он прямоугольный, а один из его острых углов равен 45°. Тогда и второй острый угол также равен 45°. То есть это равнобедренный треуг-к. Это помогает найти длину высоты DH:

ведь это прямоугольныетреуг-ки с равными гипотенузой и катетом:

Из равенства треуг-ков следует, что

Итак, сегодня мы узнали, как вычислять площади треуг-ков и некоторых видов четырехуг-ков. В большинстве случаев предварительно необходимо найти высоту в многоугольнике. В будущем мы узнаем ещё несколько формул для вычисления площадей фигур.

Формулы площади геометрических фигур

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

1. Формула площади треугольника по стороне и высоте
   Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

2. Формула площади треугольника по трем сторонам

   Формула Герона

   S = √p(p — a)(p — b)(p — c)

3. Формула площади треугольника по двум сторонам и углу между ними
   
   Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

4. Формула площади треугольника по трем сторонам и радиусу описанной окружности

5. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
   Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

   где S — площадь треугольника,
   a, b, c — длины сторон треугольника,
   h — высота треугольника,
   γ — угол между сторонами a и b,
   r — радиус вписанной окружности,
   R — радиус описанной окружности,

   p =	a + b + c	— полупериметр треугольника.
   2

Формулы площади квадрата

1. Формула площади квадрата по длине стороны
   Площадь квадрата равна квадрату длины его стороны.

   S = a²

2. Формула площади квадрата по длине диагонали
   Площадь квадрата равна половине квадрата длины его диагонали.

   где S — площадь квадрата,
   a — длина стороны квадрата,
   d — длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b

где S — Площадь прямоугольника,
a, b — длины сторон прямоугольника.

Формулы площади параллелограмма

1. Формула площади параллелограмма по длине стороны и высоте
   Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

   S = a · h

2. Формула площади параллелограмма по двум сторонам и углу между ними
   Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

   S = a · b · sin α

3. Формула площади параллелограмма по двум диагоналям и углу между ними
   Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

   где S — Площадь параллелограмма,
   a, b — длины сторон параллелограмма,
   h — длина высоты параллелограмма,
   d₁, d₂ — длины диагоналей параллелограмма,
   α — угол между сторонами параллелограмма,
   γ — угол между диагоналями параллелограмма.

Формулы площади ромба

1. Формула площади ромба по длине стороны и высоте
   Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

   S = a · h

2. Формула площади ромба по длине стороны и углу
   Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

   S = a² · sin α

3. Формула площади ромба по длинам его диагоналей
   Площадь ромба равна половине произведению длин его диагоналей.

   где S — Площадь ромба,
   a — длина стороны ромба,
   h — длина высоты ромба,
   α — угол между сторонами ромба,
   d₁, d₂ — длины диагоналей.

Формулы площади трапеции

1. Формула Герона для трапеции

   S =	a + b	√(p-a)(p-b)(p-a-c)(p-a-d)
   |a — b|

2. Формула площади трапеции по длине основ и высоте
   
   Площадь трапеции равна произведению полусуммы ее оснований на высоту

   где S — площадь трапеции,
   a, b — длины основ трапеции,
   c, d — длины боковых сторон трапеции,

   p =	a + b + c + d	— полупериметр трапеции.
   2

Формулы площади выпуклого четырехугольника

1. Формула площади четырехугольника по длине диагоналей и углу между ними

   Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

   где S — площадь четырехугольника,
   d₁, d₂ — длины диагоналей четырехугольника,
   α — угол между диагоналями четырехугольника.

2. Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)

   Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности

   S = p · r

3. 

   Формула площади четырехугольника по длине сторон и значению противоположных углов

   S = √(p — a)(p — b)(p — c)(p — d) — abcd cos²θ

   где S — площадь четырехугольника,

   a, b, c, d — длины сторон четырехугольника,

   p = a + b + c + d2 — полупериметр четырехугольника,

   θ = α + β2 — полусумма двух противоположных углов четырехугольника.

4. Формула площади четырехугольника, вокруг которого можно описать окружность

   S = √(p — a)(p — b)(p — c)(p — d)

Формулы площади круга

1. Формула площади круга через радиус
   Площадь круга равна произведению квадрата радиуса на число пи.

   S = π r²

2. Формула площади круга через диаметр
   Площадь круга равна четверти произведения квадрата диаметра на число пи.

   где S — Площадь круга,
   r — длина радиуса круга,
   d — длина диаметра круга.

Формулы площади эллипса

Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

S = π · a · b

где S — Площадь эллипса,

a — длина большей полуоси эллипса,

b — длина меньшей полуоси эллипса.