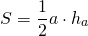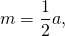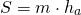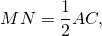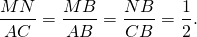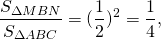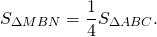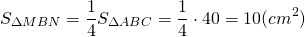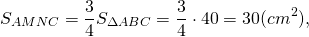Выясним, как связаны средняя линия треугольника и его площадь.

Поскольку средняя линия треугольника, соединяющая середины двух сторон, равна половине третьей стороны:
то можно найти площадь треугольника через его среднюю линию:
Вывод:
Площадь треугольника равна произведению средней линии и высоты, перпендикулярной этой средней линии.
II.Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от него подобный треугольник.

Поскольку
то
Так как площади подобных треугольников относятся как квадраты их соответствующих сторон, то
то есть
Вывод:
Средняя линия треугольника отсекает от него треугольник, площадь которого равна четверти площади исходного треугольника.
Например, если площадь треугольника ABC равна 40 см², то средняя линия MN, параллельная стороне AC, делит его площадь на части:
Площадь трапеции AMNC составляет три четверти площади треугольника ABC
или может быть найденакак разность площадей треугольников ABC и MBC.
На чтение 4 мин Просмотров 2.2к. Опубликовано 04.07.2019
Содержание
- Содержание
- Средняя линия треугольника [ править | править код ]
- Свойства [ править | править код ]
- Признаки [ править | править код ]
- Средняя линия четырёхугольника [ править | править код ]
- Свойства [ править | править код ]
- Средняя линия трапеции [ править | править код ]
Средняя линия фигур в планиметрии — отрезок, соединяющий середины двух сторон данной фигуры. Понятие употребляется для следующих фигур: треугольник, четырёхугольник, трапеция.
Содержание
Средняя линия треугольника [ править | править код ]
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника [1] .
Свойства [ править | править код ]
- средняя линия треугольника параллельна основанию и равна его половине.
- средняя линия отсекает треугольник, подобный и гомотетичный исходному с коэффициентом 1/2; его площадь равна одной четвёртой площади исходного треугольника.
- три средние линии делят исходный треугольник на четыре равных треугольника. Центральный из этих треугольников называется дополнительным или серединным треугольником.
Признаки [ править | править код ]
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок – средняя линия.
Средняя линия четырёхугольника [ править | править код ]
Средняя линия четырёхугольника — отрезок, соединяющий середины противолежащих сторон четырёхугольника.
Свойства [ править | править код ]
Первая линия соединяет 2 противоположные стороны. Вторая соединяет 2 другие противоположные стороны. Третья соединяет центры двух диагоналей (не во всех четырёхугольниках диагонали пунктом пересечения делятся пополам).
- Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
- Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
- Середины сторон произвольного четырёхугольника — вершины параллелограмма. Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона;
- Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода. Средние линии второго рода — четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона.
- Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырёхугольника.
- В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований.
Средняя линия трапеции [ править | править код ]
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.
Она рассчитывается по формуле: E F = A D + B C 2 <displaystyle EF=<frac <2>>> 
07.06.2019 
5 июня Что порешать по физике
30 мая Решения вчерашних ЕГЭ по математике
Площадь треугольника ABC равна 176, DE — средняя линия. Найдите площадь треугольника CDE.
Средняя линия отсекает от треугольника подобный ему с коэффициентом подобия Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда
Выясним, как связаны средняя линия треугольника и его площадь.

Поскольку средняя линия треугольника, соединяющая середины двух сторон, равна половине третьей стороны:
то можно найти площадь треугольника через его среднюю линию:
Площадь треугольника равна произведению средней линии и высоты, перпендикулярной этой средней линии.
II.Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от него подобный треугольник.

Так как площади подобных треугольников относятся как квадраты их соответствующих сторон, то
Средняя линия треугольника отсекает от него треугольник, площадь которого равна четверти площади исходного треугольника.
Например, если площадь треугольника ABC равна 40 см², то средняя линия MN, параллельная стороне AC, делит его площадь на части:
Площадь трапеции AMNC составляет три четверти площади треугольника ABC
или может быть найденакак разность площадей треугольников ABC и MBC.
Средняя линия треугольника и его площадь
Выясним, как связаны средняя линия треугольника и его площадь.
I. Площадь треугольника равна половине произведения основания на высоту, проведённую к этой стороне:
Поскольку средняя линия треугольника, соединяющая середины двух сторон, равна половине третьей стороны:
то можно найти площадь треугольника через его среднюю линию:
Площадь треугольника равна произведению средней линии и высоты, перпендикулярной этой средней линии.
II.Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от него подобный треугольник.
Если MN- средняя линия треугольника ABC и MN параллельна AC, то треугольники ABC и MBN подобны.
Так как площади подобных треугольников относятся как квадраты их соответствующих сторон, то
Средняя линия треугольника отсекает от него треугольник, площадь которого равна четверти площади исходного треугольника.
Например, если площадь треугольника ABC равна 40 см², то средняя линия MN, параллельная стороне AC, делит его площадь на части:
Площадь трапеции AMNC составляет три четверти площади треугольника ABC
или может быть найденакак разность площадей треугольников ABC и MBC.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.
Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
http://vsvoemdome.ru/obrazovanie/kak-nayti-ploschad-treugolnika
http://www.mozgan.ru/Geometry/AreaTriangle
Рассмотрим задачу на подобие, где требуется найти площадь треугольника, средняя линия которого делит его на части.
Утверждение.
Средняя линия треугольника делит его на треугольник и трапецию, площади которых относятся как 1:3.

FK — средняя линия
Доказать:
Доказательство:
Рассмотрим ∆ FCK и ∆ ACB
По свойству средней линии треугольника, FK∥AB и FK=1/2 AB.
Отсюда, ∠CFK=∠CAB (как соответственные при FK∥AB и секущей AC).
∠C — общий.
Следовательно, ∆ FCK и ∆ ACB подобны (по двум углам).
Так как площади подобных фигур относятся как квадраты их соответствующих линейных размеров, то
Таким образом,
а так как
Итак, средняя линия треугольника делит его на треугольник и трапецию, площади которых, соответственно, составляют одну четверть и три четверти от площади исходного треугольника, значит,
Что и требовалось доказать.
Задача.

∆ ABC,
F — середина AC,
K — середина BC,
Найти:
Решение:
Пусть
По доказанному выше утверждению,
Значит,
Поскольку
Ответ: 18 см².
Всего: 23 1–20 | 21–23
Добавить в вариант
Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
В треугольнике ABC DE — средняя линия. Площадь треугольника CDE равна 9. Найдите площадь треугольника ABC.
В треугольнике ABC отрезок DE — средняя линия. Площадь треугольника CDE равна 97. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 25. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 38. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 45. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 94. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 2. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 7. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 24. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 97. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 21. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 89. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 8. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 96. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 57. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 76. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 20. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 12. Найдите площадь треугольника ABC.
Всего: 23 1–20 | 21–23