Как найти площадь сечения конуса круг

§ 18. Конус

18.1.Определение конуса и его элементов

Определение. Тело, которое образуется при вращении прямоугольного треугольника вокруг прямой, содержащей его катет, называется прямым круговым конусом (рис. 165, 166).

Отрезок оси вращения, заключённый внутри конуса, называется осью конуса.

Круг, образованный при вращении второго катета, называется основанием конуса. Длина этого катета называется радиусом основания конуса или, короче, радиусом конуса. Вершина острого угла вращающегося треугольника, лежащая на оси вращения, называется вершиной конуса. На рисунках 165, б и 166 вершиной конуса является точка Р.

Высотой конуса называется отрезок, проведённый из вершины конуса перпендикулярно его основанию. Длину этого перпендикуляра также называют высотой конуса. Высота конуса имеет своим основанием центр круга — основания конуса — и совпадает с осью конуса.

Отрезки, соединяющие вершину конуса с точками окружности его основания, называются образующими конуса. Все образующие конуса равны между собой (почему?).

Как и в случае с цилиндром, можно рассматривать конус в более широком, чем у нас, понимании, когда в основании конуса может быть, например, эллипс (эллиптический конус), парабола (параболический конус). Мы будем изучать только определённый выше прямой круговой конус (конус вращения), поэтому слова «прямой круговой» мы будем опускать.

Поверхность, полученная при вращении гипотенузы, называется боковой поверхностью конуса, а её площадь — площадью боковой поверхности конуса и обозначается Sбок. Боковая поверхность конуса является объединением всех его образующих.

Объединение боковой поверхности конуса и его основания называется полной поверхностью конуса, а её площадь называется площадью полной поверхности конуса или, короче, площадью поверхности конуса и обозначается Sкон. Из этого определения следует, что

Sкон = Sбок + Sосн.

Если вокруг данной прямой — оси — вращать пересекающую её прямую, то при этом вращении образуется поверхность, которую называют круговой конической поверхностью или конической поверхностью вращения. Уравнение  + –  = 0 задаёт коническую поверхность вращения с осью вращения Oz (рис. 167). Из этого уравнения следует, что коническая поверхность является поверхностью второго порядка. (Подробнее о поверхностях второго порядка можно прочитать в «Дополнениях» — в конце этой книги.)

18.2. Сечения конуса

Определение. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением конуса.

Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники. На рисунке 168 осевым сечением конуса является треугольник ABP (АР = ВР). Угол АPВ называют углом при вершине осевого сечения конуса.

Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.

Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP).

Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).

Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением.

 Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками.

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги. 

 ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60°; б) в 90°. Найти площадь сечения.

Решение. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.

Хорда АВ окружности основания стягивает дугу в 60°, значит, △ AOB — правильный и АВ = R.

Рис. 172

Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S△ ABP = АВ•РC. Имеем: ОР = R (по условию); в △ AOB: ОС = ; в △ ОСР: CP =  = .

Тогда S△ ABP =  АВ•РС = .

Ответ: а) .

18.3. Касательная плоскость к конусу

Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.

Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.

Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.

18.4. Изображение конуса

Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).

Для достижения наглядности изображения невидимые линии изображают штрихами.

Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.

18.5. Развёртка и площадь поверхности конуса

Пусть l — длина образующей, R — радиус основания конуса с вершиной Р.

Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a), то получим развёртку поверхности конуса (рис. 176, б), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):

α = .

За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.

Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле

Sбок =  α•l2,(1)

где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = , получаем:

Sбок = πRl.(2)

Таким образом, доказана следующая теорема.

Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼

Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.

Sкон = πRl + πR2.(3)

Следствие. Пусть конус образован вращением прямоугольного треугольника ABC вокруг катета АС (рис. 177). Тогда Sбок = π•BC•АВ. Если D — середина отрезка АВ, то AB = 2AD, поэтому

Sбок = 2 π ВС•AD.(4)

Проведём DE ⟂ АB (E ∈ l = AС). Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А) имеем

 = ⇒ BC•AD = DE•АС.(5)

Тогда соотношение (4) принимает вид

Sбок = (2π•DE)•AC,(6)

т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.

Это следствие будет использовано в п. 19.7.

18.6. Свойства параллельных сечений конуса

Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Доказательство. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α, параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).

Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β, α || β, то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O1 = α ∩ РО.  Обозначим этот круг F1.

Рассмотрим гомотетию с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).

Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия отображает основание F конуса на его параллельное сечение — круг F1, при этом центр О основания отображается на центр О1 круга F1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии точка X отображается на точку X1 = РX ∩ α. Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:

 =  = k,(*)

где k — коэффициент гомотетии , т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.

А поскольку гомотетия является подобием, то круг F1, являющийся параллельным сечением конуса, подобен его основанию.

Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO1 : РО, где РO1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то

Sсечен : Sоснов = k2 = : PO2.

Теорема доказана. ▼

18.7.Вписанные в конус и описанные около конуса пирамиды

Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.

Для построения изображения правильной пирамиды, вписанной в конус:

—строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;

—соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;

—выделяют видимые и невидимые (штрихами) линии изображаемых фигур.

На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:

—прямоугольный треугольник (см. рис. 179);

—правильный треугольник (см. рис. 180);

—квадрат (см. рис. 181);

—правильный шестиугольник (см. рис. 182).

Определение. Пирамида называется описанной около конуса, если у них вершина общая, а основание пирамиды описано около основания конуса. В этом случае конус называют вписанным в пирамиду (рис. 183).

 ЗАДАЧА (3.080). В равносторонний конус вписана правильная пирамида. Найти отношение площадей боковых поверхностей пирамиды и конуса, если пирамида: а) треугольная; б) четырёхугольная; в) шестиугольная.

Решение. Рассмотрим случай а). Пусть R — радиус основания равностороннего конуса, РАВС — правильная пирамида, вписанная в этот конус (рис. 184); △ DPE — осевое сечение конуса, CF — медиана △ АBС. Тогда в △ АВС (правильный): АВ = R, OF = R; в △ DPE (правильный): ОР =  = R; в △ ОРF (∠ FOP = 90°):

PF =  = .

Так как CF — медиана △ АВС, то PF — высота равнобедренного треугольника АВР. Поэтому

S△ ABP =  AB•PF =  R•  = .

Обозначим: S1 — площадь боковой поверхности пирамиды, S2 — площадь боковой поверхности конуса. Тогда

S1 = 3S△ ABP = ,

S

2 = πR•PA = πR•2R = 2πR2.

Следовательно,

S1 : S2 = : 2πR2 = .

Ответ: а) .

 Во многих пособиях по геометрии за площадь боковой поверхности конуса принимают предел последовательности боковых поверхностей правильных вписанных в конус (или описанных около конуса) п-угольных пирамид при n → +∞. Действительно, Sбок. пов. пирам = •a•Poсн. пирам, где Рoсн. пирам — периметр основания пирамиды, а — апофема боковой грани. Для правильных описанных около конуса пирамид апофема a — постоянная величина, равная образующей l конуса, а предел последовательности периметров правильных многоугольников, описанных около окружности радиуса R основания конуса, равен 2πR — длине этой окружности. Таким образом, мы вновь получаем: Sбок = πRl. 

18.8. Усечённый конус

Пусть дан конус с вершиной Р. Проведём плоскость α, параллельную плоскости основания конуса и пересекающую этот конус (рис. 185). Эта плоскость пересекает данный конус по кругу и разбивает его на два тела: одно из них является конусом, а другое (расположенное между плоскостью основания данного конуса и секущей плоскостью) называют усечённым конусом. Таким образом, усечённый конус представляет собой часть полного конуса, заключённую между его основанием и параллельной ему плоскостью. Основание данного конуса и круг, полученный в сечении этого конуса плоскостью α, называются соответственно нижним и верхним основаниями усечённого конуса. Высотой усечённого конуса называется перпендикуляр, проведённый из какой-либо точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённого конуса. (Часто за высоту усечённого конуса принимают отрезок, соединяющий центры его оснований.)

Часть боковой поверхности данного конуса, ограничивающая усечённый конус, называется боковой поверхностью усечённого конуса, а отрезки образующих конуса, заключённые между основаниями усечённого конуса, называются образующими усечённого конуса. Так как все образующие данного конуса равны и равны все образующие отсечённого конуса, то равны все образующие усечённого конуса.

Построение изображения усечённого конуса следует начинать с изображения того конуса, из которого получился усечённый конус (рис. 186).

На рисунке 187 показана развёртка усечённого конуса.

Из теоремы 28 следует, что основания усечённого конуса — подобные круги.

Определения усечённой пирамиды, вписанной в усечённый конус и описанной около него, аналогичны определениям пирамиды, вписанной в конус и описанной около него.

Заметим, что построение изображений усечённой пирамиды, вписанной в усечённый конус и описанной около него, следует начинать с изображений того конуса или той пирамиды, из которых получены соответственно усечённые конус и пирамида.

Полной поверхностью усечённого конуса называется объединение боковой поверхности этого конуса и двух его оснований. Иногда полную поверхность усечённого конуса называют его поверхностью, а её площадь — площадью поверхности усечённого конуса. Эта площадь равна сумме площадей боковой поверхности и оснований усечённого конуса.

Усечённый конус может быть образован также вращением прямоугольной трапеции вокруг боковой стороны трапеции, перпендикулярной её основанию.

На рисунке 188 изображён усечённый конус, образованный вращением прямоугольной трапеции ABCD вокруг стороны CD. При этом боковая поверхность усечённого конуса образована вращением боковой стороны АВ, а основания его — вращением оснований AD и ВС трапеции.

18.9. Поверхность усечённого конуса

Выразим площадь Sбок боковой поверхности усечённого конуса через длину l его образующей и радиусы R и r оснований (R > r).

Пусть точка Р — вершина конуса, из которого получен усечённый конус; точки О, O1 — центры оснований усечённого конуса; AA1 = l — одна из образующих усечённого конуса (рис. 189).

Используя формулу (2) п. 18.5, получаем

Учитывая, что A1A = l, имеем

Sбок = πRl + π(R – r)PA1.(7)

Выразим PA1 через l, R и r. Так как O1A1 || OA и OO1 — высота усечённого конуса, то прямоугольные треугольники POA и PO1A1 подобны. Поэтому АО : А1O1 = PA : PA1 или

Подставив это значение РА1 в (7), получаем

Sбок = π(R + r)l.(8)

Таким образом, доказана следующая теорема.

Теорема 29. Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую. ▼

Площадь полной поверхности усечённого конуса находится по формуле:

Sполн = π•(R + r)•l + π•R2 + π•r2.

Следствие. Пусть усечённый конус образован вращением прямоугольной трапеции ABCD вокруг её высоты AD (рис. 190). Тогда Sбок = π (АВ + DC)•ВС. Если KЕ — средняя линия трапеции, то АВ + DC = 2KE, поэтому

Sбок = 2π•KE•BC.(9)

Проведём EF ⟂ ВС.  Из подобия прямоугольных треугольников ВСН и EFK имеем

BC : EF = BH : KE ⇒ ⇒ KE•BC = EF•BH.(10)

Тогда равенство (9) принимает вид

Sбок = (2π•EF)•ВH,(11)

т. е. боковая поверхность усечённого конуса равна произведению его высоты на длину окружности, радиус которой равен серединному перпендикуляру, проведённому из точки оси конуса к его образующей.

18.10. Объёмы конуса и усечённого конуса

Найдём объём конуса, высота которого равна h и радиус основания — R. Для этого расположим этот конус и правильную четырёхугольную пирамиду, высота которой равна h и сторона основания — R, так, чтобы их основания находились на одной и той же плоскости α, а вершины — также в одной и той же плоскости β, параллельной плоскости α и удалённой от неё на расстояние h (рис. 191).

Каждая плоскость, параллельная данным плоскостям и пересекающая конус, пересекает также пирамиду; причём площади сечений, образованных при пересечении обоих тел, относятся к площадям оснований этих тел, как квадраты их расстояний от вершин. А так как секущие плоскости для пирамиды и для конуса равноудалены от их вершин, то  = . Тогда  =  =  = π, значит, для объёмов этих тел выполняется:

Vкон : Vпир = π : 1 или Vкон :  R2•h = π : 1, откуда

Vкон =  πR2 •h.

Самостоятельно рассмотрите усечённые конус и пирамиду, расположенные в соответствии с условиями принципа Кавальери. Тогда вы получите формулу вычисления объёма усечённого конуса:

Vус. кон =  π•h•(R2 + r•R + r2).

Эту же формулу вы можете вывести, если используете идею подобия так же, как это сделано в случае с выводом формулы площади боковой поверхности усечённого конуса.

Используя принцип Кавальери, докажите, что объём каждого из тел, на которые конус разбивается его сечением плоскостью, проходящей через вершину (рис. 192), может быть вычислен по формуле V =  •h•Scегм, где h — длина высоты конуса, а Sceгм — площадь соответствующего сегмента основания конуса.

Площадь сечения конуса. Для вас представлена очередная статья с конусами. На момент написания этой статьи на блоге решены все примеры (прототипы) заданий с конусами, которые возможны на экзамене. Процесс решения несложен (1-2 действия), при определённой практике решаются устно. Нужно знать понятие образующей, об этом информация в этой статье. Так же необходимо понимать как образуются сечения конуса.

1. Если плоскость проходит через вершину конуса, то сечением является треугольник.

*Если плоскость проходит через ось конуса, то сечением является равнобедренный треугольник, высота которого равна высоте конуса, а основание на которое опущена эта высота равна диаметру основания конуса.

2. Если плоскость проходит перпендикулярно оси конуса, то сечением является круг.

Особенностью данных заданий является то, что применяется формула площади треугольника, здесь она первая. Формулы периодически повторяйте. Рассмотрим задачи:

324453. Площадь основания конуса равна 16Пи, высота равна 6. Найдите площадь осевого сечения конуса.

Осевым сечением конуса является треугольник с основанием равным диаметру основания конуса и высотой равной высоте конуса. Обозначим диаметр как D, высоту как Н, запишем формулу площади треугольника:

Высота известна, вычислим диаметр. Используем формулу площади круга:

Значит диаметр будет равен 8. Вычисляем площадь сечения:

Ответ: 24

324454. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Сечением является круг. Необходимо найти площадь этого круга.

Построим осевое сечение:

Рассмотрим треугольники AKL и AOC – они подобны. Известно, что в подобных фигурах отношения соответствующих элементов равны. Мы рассмотрим отношения высот и катетов (радиусов):

OC  это радиус основания, его можно найти:

Значит

Теперь можем вычислить площадь сечения:

*Это алгебраический способ вычисления без использования свойства подобных тел, касающегося их площади. Можно было рассудить так:

Два конуса (исходный и отсечённый) подобны, значит пощади их оснований являются подобными фигурами. Для площадей подобных фигур существует зависимость:

Коэффициент подобия в данном случае равен 1/3 (высота исходного конуса равна 9, отсечённого 3), 3/9=1/3.

Таким образом, площадь основания полученного конуса равна:

Ответ: 2

323455. Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.

Пусть образующая это L, высота это H, радиус основания это R.

Найдём диаметр основания и используя формулу площади треугольника вычислим площадь. По теореме Пифагора:

Вычисляем площадь сечения:

Ответ: 48

Диаметр основания конуса равен 40, а длина образующей — 25. Найдите площадь осевого сечения этого конуса.

Пусть образующая это L, высота это H, радиус основания это R. 

Радиус основания равен половине диаметра, то есть 20.

Вычислим высоту и далее используя формулу площади треугольника найдём искомую площадь. По теореме Пифагора:

Вычисляем площадь сечения:

Ответ: 300

На этом всё. Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Осевым сечением конуса в треугольнике, является не что иное, как произведение его длины и высоты. То есть по сути, это все внутренне пространство, которое есть внутри треугольника, а так как его образует как длина этого самого треугольника, так и его радиус, то для того что бы его найти, нужно две эти величины, просто между собой, перемножить. автор вопроса выбрал этот ответ лучшим Степа­н-16 [34.5K] 6 лет назад  Осевым сечением конуса является равнобедренный треугольник. Соответственно, площадь осевого сечения будет определяться формулой площади треугольника и равна половине произведения основания треугольника (или диаметра окружности — основания конуса) на высоту треугольника (или конуса). Если проще, то: произведению радиуса основания конуса на его высоту. Ankla­v [4.4K] 8 лет назад  Вообразите себе конус и разделите его на две части сверху вниз. Это будет треугольник . А формулу, как найти площади его, вы знаете: S = 1/2D h = R * h На самом деле, нахождение площади сечения в случаях в стереометрии сводится к понятиям обычной геометрии на плоскости Ксарф­акс [156K] 6 лет назад  Определение из курса стереометрии: Осевое сечение — это сечение трёхмерной фигуры плоскостью, которая проходит через ось этой фигуры. Для конуса осевым сечением будут являться треугольник. Таким образом, для нахождения площади осевого сечения конуса необходимо найти площадь данного треугольника. Площадь треугольника равна половине произведения основания на высоту, проведённую к данному основанию. Высота треугольника будет совпадать с высотой конуса, она равна h. Основание треугольника будет равно диаметру окружности d (окружность является основанием конуса). Таким образом, S = 0,5*d*h. Так как половина диаметра окружности — это радиус, то формулу можно переписать в следующем виде: Sсеч = R*h. Пчела Жужа [77.9K] 6 лет назад  Площадь осевого сечения конуса можно высчитать, применив формулу S=1/2d*h=Rh, где S является площадью осевого сечения, R является радиусом, d является диаметром конуса, а h — это высота конуса. Стоит отметить, что осевым сечением является треугольник. Площадь осевого сечения конуса вычисляется по формуле: S=1/2*(h*2r),где h -это высота,r-это радиус основания.Например.если высота конуса равна 5 см, а радиус основания равен 2,5 см, то площадь осевого сечения будет равна S=0.5*(5*2*2.5)=12.5 cm Антон­75 [206] 8 лет назад  Осевое сечение конуса — это треугольник.Следовательно, площадь осевого сечения конуса равна произведению высоты конуса на радиус основания. S=h*r Oleg7­4 [203K] 8 лет назад  При осевом сечении конуса плоскость проходит через вершину данного конуса , а самим сечением получается треугольник. Площадью такого сечения является половина диаметра или радиуса, умноженного на высоту. То есть формула вычисления такой площади выглядит так : S = 1/2D h = R h где D — это диаметр конуса ( основания ), R — радиус основания, а h — это высота конуса и треугольника, соответственно. morel­juba [62.5K] 6 лет назад  В первую очередь хочу отметить тот факт, что осевое сечение конуса представляет собой треугольник. Этот факт означает что от нас требуется найти площадь данного треугольника. Найдём площадь вот по этой формуле: В данной формуле диаметр конуса — это D. Радиус основания — это R, а высотой конуса здесь является h. timur­ovec [273K] 8 лет назад  Для ответа необходимо хорошее пространственное представление. Если конус разделить от вершины до средины основания , мы получим фигуру треугольника. А площадь треугольника высчитывается произведением высоты на длину нижней стороны , деленную на два , в данном случае это радиус. Ksyus­ha26 [26.8K] 8 лет назад  Надо сказать, что сечение представляет собой ни что иное, как треугольник. То есть найти площадь осевого сечения конуса можно найти с помощью следующей формулы: S=1/2d*h=Rh. D признается диаметром конуса, R признается радиусом основания, h является высотой конуса Знаете ответ?

Круглый конус в геометрии является симметричной пространственной фигурой, имеющей ось вращения. Одной из важных его характеристик является площадь сечения осевого. В данной статье приведем формулу площади сечения осевого конуса прямого с круглым основанием и усеченного.

О какой фигуре будет идти речь?

Круглый конус — это фигура, которую можно получить следующим образом. Необходимо взять треугольник с углом прямым и его вокруг одного из катетов вращать. Тогда получится показанная ниже объемная фигура.

Отрезок AC на рисунке называется радиусом основания, который «рисует» при вращении с центром в точке A круг. Катет AB — это высота конуса. Очевидно, что отрезок AB перпендикулярен основанию и является частью оси вращения фигуры. Точка B — это высота рассматриваемой фигуры. Отрезок BE называется образующей, или генератрисой конуса. Совокупность всех генератрис образует боковую поверхность конуса. Она является конической. Ограничивающая основание окружность называется направляющей, или директрисой конуса.

Поскольку генератриса, радиус и высота являются гипотенузой и катетами рассмотренного прямоугольного треугольника, то для них можно записать формулу:

g² = r² + h²

Здесь g — генератриса, r — радиус, h — высота.

Осевое сечение конуса и его площадь

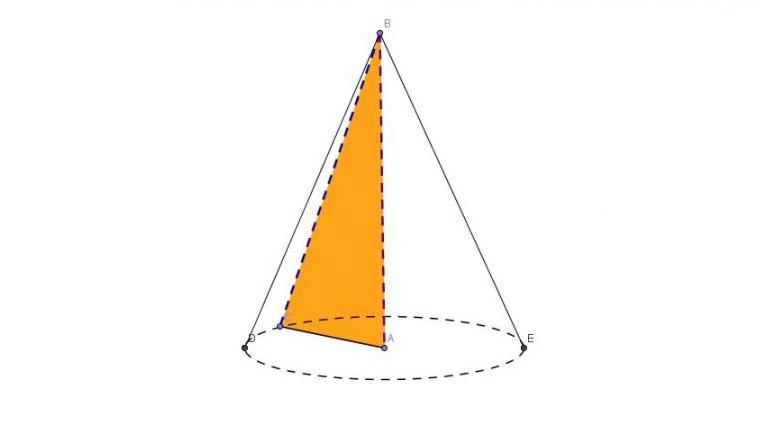
Чтобы записать для конуса формулу площади сечения осевого, сначала следует познакомиться с самим сечением. Оно получается так: нужно взять секущую плоскость, расположить ее параллельно оси конуса. Затем необходимо разрезать конус плоскостью на две одинаковые части таким образом, чтобы в плоскость сечения попала вершина фигуры.

Несложно себе представить, что в результате описанной операции получится равнобедренный треугольник. Равные стороны треугольника будут такие же, как длины генератрис. А третья сторона будет равна диаметру основания.

Формула площади осевого сечения конуса (фото см. выше) не отличается сложностью. Она соответствует формуле расчета этой величины для описанного треугольника. Поскольку у треугольника площадь равна произведению основания на высоту, которое следует поделить пополам, то искомое равенство для осевого сечения примет вид:

S = h*r

Эта формула говорит о том, что S в два раза больше площади прямоугольного треугольника, вращением которого был получен конус.

Усеченный конус и его осевое сечение

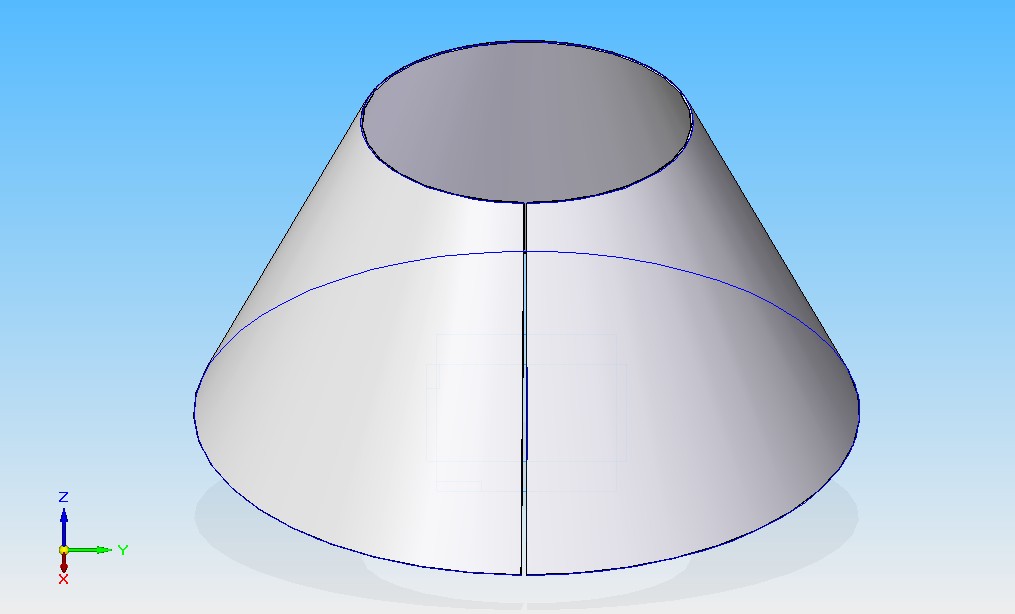
Усеченный конус получается из обычного при помощи секущей плоскости, которая параллельна его основанию. Полученная при этом фигура под плоскостью будет усеченным конусом. Он показан на рисунке.

Помимо боковой поверхности, эта фигура состоит из двух оснований, которые представляют собой большой и малый круги. Обозначим их радиусы как r₁ и r₂. Расстояние между основаниями называется высотой, обозначим ее буквой h.

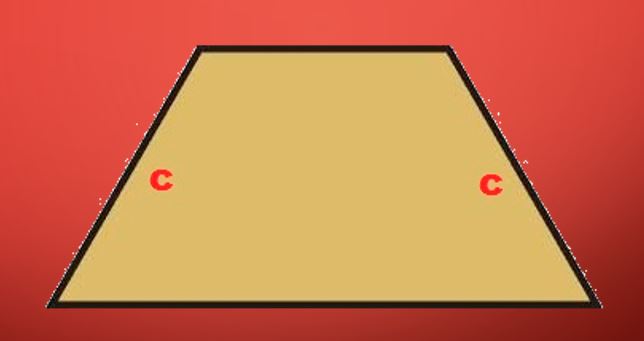
Осевое сечение рассматриваемого конуса будет четырехугольником, две стороны которого являются образующими. А две другие стороны будут параллельны друг другу и равны 2*r₁ и 2*r₂ соответственно. Этот четырехугольник будет равнобедренной трапецией, которая показана на рисунке ниже.

Этот факт позволяет использовать выражение для трапеции, чтобы записать формулу площади сечения усеченного осевого конуса . Она примет вид:

S = (2*r₁ + 2*r₂)/2*h = h*(r₁ + r₂)

То есть площадь S равна произведению суммы радиусов оснований усеченного конуса на его высоту.

Для решения геометрических задач также может потребоваться формула связи между генератрисой фигуры и ее параметрами r₁, r₂ и h. Соответствующее выражение приобретает вид:

g² = h² + (r₁ — r₂)²

Получить ее достаточно просто самостоятельно, если рассмотреть прямоугольный треугольник внутри конуса, построенный на сторонах g, h и (r₁ — r₂).

Задача на определение площади сечения осевого конуса усеченного

Покажем, как находить площадь осевого сечения на примере усеченного конуса.

Известно, что высота указанной фигуры составляет 10 см. Также известно, что для конуса осевого сечения площадь равна разности площадей оснований. Зная, что диаметры оснований отличаются ровно в два раза, необходимо найти площадь этого сечения по оси.

В соответствии с условием задачи можно записать два уравнения:

r₁ = 2*r₂;

h*(r₁ + r₂) = pi*(r₁² — r₂²)

Значение высоты известно из условия. Таким образом, мы имеем 2 равенства и 2 неизвестные величины. Решаем эту систему:

h*(2*r₂ + r₂) = pi*((2*r₂) ² — r₂²) =>

3*pi*r₂² — 3*h*r₂ = 0

Мы получили неполное квадратное уравнение, которое следует решить относительно переменной r₂. Уравнение имеет 2 корня, но решение r₂ = 0 не является физическим, поэтому запишем только одно единственное значение для малого радиуса:

r₂ = h/pi

Тогда большой радиус r₁ будет равен:

r₁ = 2*h/pi

Подставляя эти равенства в формулу площади осевого сечения конуса, получаем:

S = h*(r₁ + r₂) = 3*h²/pi

Подставляем численное значение h и записываем ответ: S ≈ 95,54 см².

Просмотры: 16

Круглый конус в геометрии является симметричной пространственной фигурой, имеющей ось вращения. Одной из важных его характеристик является площадь сечения осевого. В данной статье приведем формулу площади сечения осевого конуса прямого с круглым основанием и усеченного.

О какой фигуре будет идти речь?

Круглый конус — это фигура, которую можно получить следующим образом. Необходимо взять треугольник с углом прямым и его вокруг одного из катетов вращать. Тогда получится показанная ниже объемная фигура.

Отрезок AC на рисунке называется радиусом основания, который «рисует» при вращении с центром в точке A круг. Катет AB — это высота конуса. Очевидно, что отрезок AB перпендикулярен основанию и является частью оси вращения фигуры. Точка B — это высота рассматриваемой фигуры. Отрезок BE называется образующей, или генератрисой конуса. Совокупность всех генератрис образует боковую поверхность конуса. Она является конической. Ограничивающая основание окружность называется направляющей, или директрисой конуса.

Поскольку генератриса, радиус и высота являются гипотенузой и катетами рассмотренного прямоугольного треугольника, то для них можно записать формулу:

g² = r² + h²

Здесь g — генератриса, r — радиус, h — высота.

Осевое сечение конуса и его площадь

Чтобы записать для конуса формулу площади сечения осевого, сначала следует познакомиться с самим сечением. Оно получается так: нужно взять секущую плоскость, расположить ее параллельно оси конуса. Затем необходимо разрезать конус плоскостью на две одинаковые части таким образом, чтобы в плоскость сечения попала вершина фигуры.

Несложно себе представить, что в результате описанной операции получится равнобедренный треугольник. Равные стороны треугольника будут такие же, как длины генератрис. А третья сторона будет равна диаметру основания.

Формула площади осевого сечения конуса (фото см. выше) не отличается сложностью. Она соответствует формуле расчета этой величины для описанного треугольника. Поскольку у треугольника площадь равна произведению основания на высоту, которое следует поделить пополам, то искомое равенство для осевого сечения примет вид:

S = h*r

Эта формула говорит о том, что S в два раза больше площади прямоугольного треугольника, вращением которого был получен конус.

Усеченный конус и его осевое сечение

Усеченный конус получается из обычного при помощи секущей плоскости, которая параллельна его основанию. Полученная при этом фигура под плоскостью будет усеченным конусом. Он показан на рисунке.

Помимо боковой поверхности, эта фигура состоит из двух оснований, которые представляют собой большой и малый круги. Обозначим их радиусы как r₁ и r₂. Расстояние между основаниями называется высотой, обозначим ее буквой h.

Осевое сечение рассматриваемого конуса будет четырехугольником, две стороны которого являются образующими. А две другие стороны будут параллельны друг другу и равны 2*r₁ и 2*r₂ соответственно. Этот четырехугольник будет равнобедренной трапецией, которая показана на рисунке ниже.

Этот факт позволяет использовать выражение для трапеции, чтобы записать формулу площади сечения усеченного осевого конуса . Она примет вид:

S = (2*r₁ + 2*r₂)/2*h = h*(r₁ + r₂)

То есть площадь S равна произведению суммы радиусов оснований усеченного конуса на его высоту.

Для решения геометрических задач также может потребоваться формула связи между генератрисой фигуры и ее параметрами r₁, r₂ и h. Соответствующее выражение приобретает вид:

g² = h² + (r₁ — r₂)²

Получить ее достаточно просто самостоятельно, если рассмотреть прямоугольный треугольник внутри конуса, построенный на сторонах g, h и (r₁ — r₂).

Задача на определение площади сечения осевого конуса усеченного

Покажем, как находить площадь осевого сечения на примере усеченного конуса.

Известно, что высота указанной фигуры составляет 10 см. Также известно, что для конуса осевого сечения площадь равна разности площадей оснований. Зная, что диаметры оснований отличаются ровно в два раза, необходимо найти площадь этого сечения по оси.

В соответствии с условием задачи можно записать два уравнения:

r₁ = 2*r₂;

h*(r₁ + r₂) = pi*(r₁² — r₂²)

Значение высоты известно из условия. Таким образом, мы имеем 2 равенства и 2 неизвестные величины. Решаем эту систему:

h*(2*r₂ + r₂) = pi*((2*r₂) ² — r₂²) =>

3*pi*r₂² — 3*h*r₂ = 0

Мы получили неполное квадратное уравнение, которое следует решить относительно переменной r₂. Уравнение имеет 2 корня, но решение r₂ = 0 не является физическим, поэтому запишем только одно единственное значение для малого радиуса:

r₂ = h/pi

Тогда большой радиус r₁ будет равен:

r₁ = 2*h/pi

Подставляя эти равенства в формулу площади осевого сечения конуса, получаем:

S = h*(r₁ + r₂) = 3*h²/pi

Подставляем численное значение h и записываем ответ: S ≈ 95,54 см².