Как найти площадь сечения призмы
Призма — это многогранник, основанием которого служат равные многоугольники, боковыми гранями — параллелограммы. Для того чтобы найти площадь сечения призмы, необходимо знать, какое сечение рассматривается в задании. Различают перпендикулярное и диагональное сечение.

Инструкция
Способ расчета площади сечения также зависит от данных, которые уже имеются в задаче. Кроме этого, решение определяется тем, что лежит в основании призмы. Если необходимо найти диагональное сечение призмы, найдите длину диагонали, которая равна корню из суммы (основания сторон в квадрате). Например, если основания сторон прямоугольника равны 3 см и 4 см, соответственно, длина диагонали равна корню из (4х4+3х3)= 5 см. Площадь диагонального сечения найдите по формуле: диагональ основания умножить на высоту.
Если в основании призмы находится треугольник, для вычисления площади сечения призмы используйте формулу: 1/2 часть основания треугольника умножить на высоту.
В случае, если в основании находится круг, площадь сечения призмы найдите умножением числа «пи» на радиус заданной фигуры в квадрате.
Различают следующие виды призм — правильные и прямые. Если необходимо найти сечение правильной призмы, вам нужно знать длину только одной из сторон многоугольника, ведь в основании лежит квадрат, у которого все стороны равны. Найдите диагональ квадрата, которая равна произведению его стороны на корень из двух. После этого перемножив диагональ и высоту, вы получите площадь сечения правильной призмы.
Призма имеет свои свойства. Так, площадь боковой поверхности произвольной призмы вычисляется по формуле, где — периметр перпендикулярного сечения, — длина бокового ребра. При этом перпендикулярное сечение перпендикулярно ко всем боковым ребрам призмы, а его углы — это линейные углы двугранных углов при соответствующих боковых ребрах. Перпендикулярное сечение перпендикулярно и ко всем боковым граням.
Источники:
- диагональное сечение призмы
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Совет 1: Как обнаружить площадь сечения призмы
Призма — это многогранник, основанием которого служат равные многоугольники, боковыми гранями — параллелограммы. Для того дабы обнаружить площадь сечения призмы, нужно знать, какое сечение рассматривается в задании. Различают перпендикулярное и диагональное сечение.
Инструкция
1. Метод расчета площади сечения также зависит от данных, которые теснее имеются в задаче. Помимо этого, решение определяется тем, что лежит в основании призмы. Если нужно обнаружить диагональное сечение призмы, обнаружьте длину диагонали, которая равна корню из суммы (основания сторон в квадрате). Скажем, если основания сторон прямоугольника равны 3 см и 4 см, соответственно, длина диагонали равна корню из (4х4+3х3)= 5 см. Площадь диагонального сечения обнаружьте по формуле: диагональ основания умножить на высоту.
2. Если в основании призмы находится треугольник, для вычисления площади сечения призмы используйте формулу: 1/2 часть основания треугольника умножить на высоту.
3. В случае, если в основании находится круг, площадь сечения призмы обнаружьте умножением числа «пи» на радиус заданной фигуры в квадрате.
4. Различают следующие виды призм — положительные и прямые. Если нужно обнаружить сечение положительной призмы, вам надобно знать длину только одной из сторон многоугольника, чай в основании лежит квадрат, у которого все стороны равны. Обнаружьте диагональ квадрата, которая равна произведению его стороны на корень из 2-х. Позже этого перемножив диагональ и высоту, вы получите площадь сечения верной призмы.
5. Призма имеет свои свойства. Так, площадь боковой поверхности произвольной призмы вычисляется по формуле, где — периметр перпендикулярного сечения, — длина бокового ребра. При этом перпендикулярное сечение перпендикулярно ко каждым боковым ребрам призмы, а его углы — это линейные углы двугранных углов при соответствующих боковых ребрах. Перпендикулярное сечение перпендикулярно и ко каждому боковым граням.
Совет 2: Как обнаружить диагональ осевого сечения
Осевым именуется сечение, которое проходит через ось геометрического тела, образованного при вращении некой геометрической фигуры. Цилиндр получается в итоге вращения прямоугольника вокруг одной из сторон, и этим обусловлены многие его свойства. Образующие этого геометрического тела параллельны и равны между собой, что дюже главно для определения параметров его осевого сечения, в том числе диагонали.
Вам понадобится
- – цилиндр с заданными параметрами;
- – лист бумаги;
- – карандаш;
- – линейка;
- – циркуль;
- – теорема Пифагора;
- – теоремы синусов и косинусов.
Инструкция
1. Постройте цилиндр согласно заданным условиям. Для того дабы его начертить, вам нужно знать радиус основания и высоту. Впрочем в задаче на определение диагонали могут быть указаны и другие данные — скажем, угол между диагональю и образующей либо диаметром основания. В этом случае при создании чертежа используйте тот размер, тот, что вам задан. Остальные возьмите произвольно и укажите, что именно вам дано. Обозначьте точки пересечения оси и оснований как О и О’.
2. Начертите осевое сечение. Оно представляет собой прямоугольник, два стороны которого являются диаметрами оснований, а две другие — образующими. От того что и образующие перпендикулярны основаниям, они являются единовременно и высотами данного геометрического тела. Обозначьте получившийся прямоугольник как АВСD. Проведите диагонали АС и ВD. Припомните свойства диагоналей прямоугольника. Они равны между собой и делятся в точке пересечения напополам.
3. Разглядите треугольник АDC. Он прямоугольный, от того что образующая CD перпендикулярна основанию. Один катет представляет собой диаметр основания, 2-й — образующую. Диагональ является гипотенузой. Припомните, как вычисляется длина гипотенузы всякого прямоугольного треугольника. Она равна квадратному корню из суммы квадратов катетов. То есть в данном случае d=?4r2+h2, где d – диагональ, r – радиус основания, а h – высота цилиндра.
4. Если в задаче высота цилиндра не дана, но указан угол диагонали осевого сечения с основанием либо образующей, используйте теорему синусов либо косинусов. Припомните, что обозначают данные тригонометрические функции. Это отношения противолежащего либо прилежащего заданному угол катета к гипотенузе, которую вам и необходимо обнаружить. Возможен, вам заданы высота и угол CAD между диагональю и диаметром основания. В этом случае используйте теорему синусов, от того что угол CAD находится наоборот образующей. Обнаружьте гипотенузу d по формуле d=h/sinCAD. Если же вам задан радиус и данный же угол, используйте теорему косинусов. В этом случае d=2r/cos CAD.
5. По тому же тезису действуйте и в тех случаях, когда заданы угол ACD между диагональю и образующей. В этом случае теорема синусов применяется, когда дан радиус, а косинусов — если вестима высота.
Видео по теме
Совет 3: Как обнаружить золотое сечение
Золотое сечение — пропорция, которую издавна считали особенно идеальной и слаженной. Она заложена в основу конструкций множества древних сооружений, от статуй до храмов, и дюже зачастую встречается в природе. Совместно с тем эта пропорция выражается изумительно изысканными математическими конструкциями.
Инструкция
1. Золотая пропорция определяется дальнейшим образом: это такое разбиение отрезка на две части, что меньшая часть относится к большей так же, как огромная часть — ко каждому отрезку.
2. Если длину каждого отрезка принять за 1, а длину большей части — за x, то желанная пропорция выразится уравнением:(1 – x)/x = x/1.Умножая обе части пропорции на x и перенося слагаемые, получаем квадратное уравнение:x^2 + x – 1 = 0.
3. Уравнение имеет два действительных корня, из которых нас, безусловно, волнует только позитивный. Он равен (?5 – 1)/2, что приблизительно равняется 0,618. Это число и выражает золотое сечение. В математике его почаще каждого обозначают буквой ?.
4. Число ? владеет рядом восхитительных математических свойств. Скажем, даже из начального уравнения видно, что 1/? = ? + 1. Подлинно, 1/(0,618) = 1,618.
5. Иной метод вычислить золотую пропорцию состоит в применении безграничной дроби. Начиная с всякого произвольного x, дозволено ступенчато возвести дробь:x1/(x + 1)1/(1/(x+1) + 1)1/(1/(1/(x+1) + 1) +1)и так дальше.
6. Для упрощения вычислений эту дробь дозволено представить в виде итеративной процедуры, в которой для вычисления дальнейшего шага необходимо прибавить единицу к итогу предыдущего шага и поделить единицу на получившееся число. Иными словами:x0 = xx(n + 1) = 1/(xn + 1).Данный процесс сходится, и его предел равен ? + 1.
7. Если заменить вычисление обратной величины извлечением квадратного корня, то есть провести итеративный цикл:x0 = xx(n + 1) = ?(xn + 1),то итог останется постоянным: самостоятельно от первоначально выбранного x итерации сходятся к значению ? + 1.
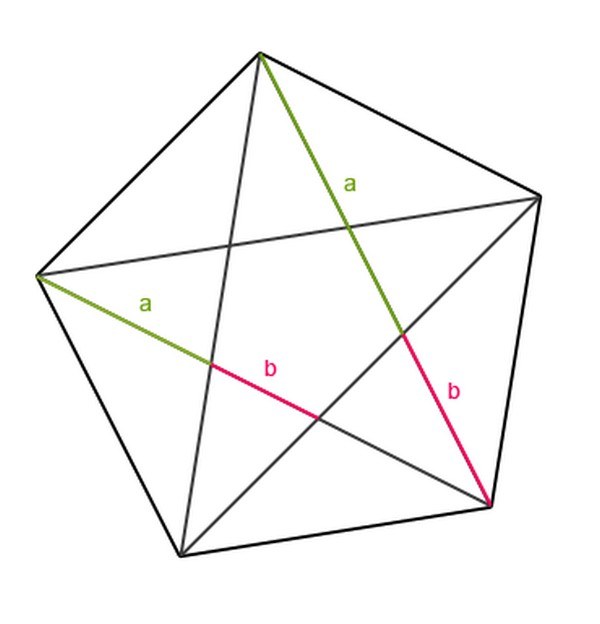
8. Геометрически золотое сечение дозволено возвести при помощи положительного пятиугольника. Если провести в нем две пересекающиеся диагонали, то всякая из них поделит иную сурово в золотом соотношении. Это слежение, согласно преданию, принадлежит Пифагору, тот, что был так ошеломлен обнаруженной обоснованностью, что счел положительную пятиконечную звезду (пентаграмму) священным священным символом.
9. Поводы, по которым именно золотое сечение кажется человеку особенно слаженным, незнакомы. Впрочем эксперименты многократно подтверждали, что испытуемые, которым было возложено особенно прекрасно поделить отрезок на две неравные части, делают это в пропорциях, крайне близких к золотому соотношению.
Совет 4: Как обнаружить площадь сечения куба
Вопрос относится к аналитической геометрии. Он решается с привлечением уравнений пространственных прямых и плоскостей, представления куба и его геометрических свойств, а также с применением векторной алгебры. Могут потребоваться методы рения систем линейных уравнений.
Инструкция
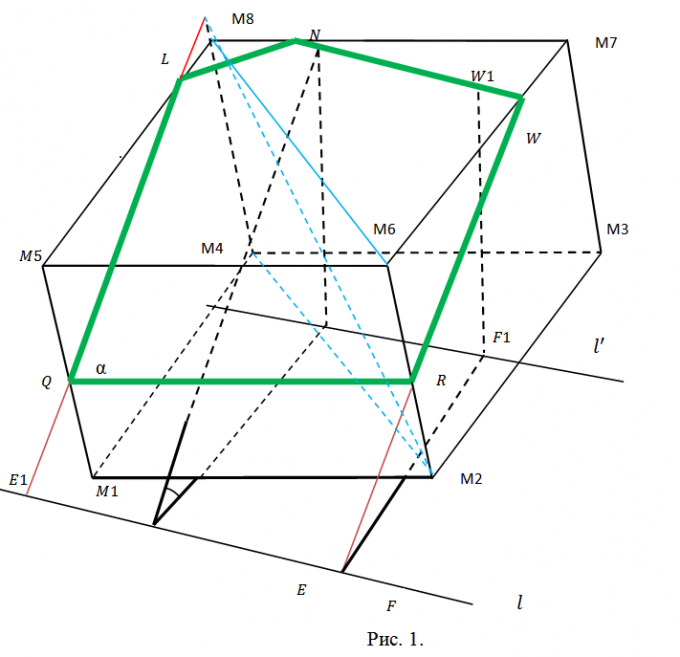
1. Выберите данные задачи так, дабы они были исчерпывающими, но не избыточными. Секущую плоскость ? следует задать всеобщим уравнением вида Ax+By+Cz+D=0, что наилучшим образом согласуется с произвольным его выбором. Для задания куба абсолютно хватит координат всяких 3 его вершин. Возьмите, скажем, точки M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3), в соответствии с рисунком 1. На этом рисунке проиллюстрировано сечение куба. Оно пересекает два боковых ребра и три ребра оснований.
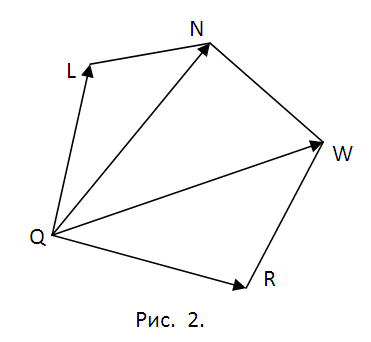
2. Определитесь с планом последующей работы. Предстоит искать координаты точек Q, L, N, W, R пересечения сечения с соответствующими ребрами куба. Для этого придется находить уравнения прямых, содержащих эти ребра, и искать точки пересечения ребер с плоскостью ?. Позже этого последует разбиение пятиугольника QLNWR на треугольники (см. рис. 2) и вычисление пощади всякого из них с поддержкой свойств векторного произведения. Методология всякий раз одна и та же. Следственно дозволено ограничиться точками Q и L и площадью треугольника ?QLN.
3. Направляющий вектор h прямой, содержащий ребро М1М5 (и точку Q), обнаружьте как векторное произведение M1M2={x2-x1, y2-y1, z2-z1} и M2M3={x3-x2, y3-y2, z3-z2}, h={m1, n1, p1}=[M1M2? M2M3]. Полученный вектор является направляющим и для всех прочих боковых ребер. Длину ребра куба обнаружьте как, скажем, ?=?( (x2-x1)^2+(y2-y1)^2+(z2-z1)^2). Если модуль вектора h |h|??, то замените его соответствующим коллинеарным вектором s={m, n, p}=(h/|h|)?. Сейчас запишите уравнение прямой, содержащей М1М5 параметрически (см. рис. 3). Позже подстановки соответствующих выражений в уравнение секущей плоскости получите А(x1+mt)+B(y1+nt)+C(z1+pt)+D=0. Определите t, подставьте в уравнения для М1М5 и запишите координаты точки Q(qx, qy, qz) (рис. 3).
4. Видимо, что точка М5 имеет координаты М5(x1+m, y1+n, z1+p). Направляющий вектор для прямой, содержащей ребро М5М8 совпадает с М2М3={x3-x2, y3-y2,z3-z2}. После этого повторите предыдущие рассуждения касательно точки L(lx, ly, lz) (см. рис. 4). Все последующее, для N(nx, ny, nz) – точная копия это шага.
5. Запишите векторы QL={lx-qx, ly-qy, lz-qz} и QN={nx-qx, ny-qy, nz-qz}. Геометрический толк их векторного произведения состоит в том, что его модуль равен площади параллелограмма построенного на векторах. Следственно площадь ?QLN S1=(1/2)|[QL? QN]|. Следуйте предложенной методике и вычислите площади треугольников ?QNW и ?QWR – S1 и S2. Векторное произведение комфортнее каждого находить с поддержкой вектора-определителя (см. рис. 5). Запишите окончательный результат S=S1+S2+S3.
Совет 5: Как обнаружить площадь диагонального сечения призмы
Призма — это многогранник с двумя параллельными основаниями и боковыми гранями в форме параллелограмма и в числе, равном числу сторон многоугольника основания.
Инструкция
1. В произвольной призме боковые ребра расположены под углом к плоскости основания. Частным случаем является прямая призма. В ней боковые стороны лежат в плоскостях, перпендикулярных основаниям. В прямой призме боковые грани — прямоугольники, а боковые ребра равны высоте призмы.
2. Диагональное сечение призмы — часть плоскости, всецело заключенная во внутреннем пространстве многогранника. Диагональное сечение может быть ограничено двумя боковыми ребрами геометрического тела и диагоналями оснований. Видимо, что число допустимых диагональных сечений при этом определяется числом диагоналей в многоугольнике основания.
3. Либо границами диагонального сечения могут служить диагонали боковых граней и противоположные стороны оснований призмы. Диагональное сечение прямоугольной призмы имеет форму прямоугольника. В всеобщем случае произвольной призмы форма диагонального сечения – параллелограмм.
4. В прямоугольной призме площадь диагонального сечения S определяется по формулам:S=d*Hгде d — диагональ основания, H — высота призмы.Либо S=a*Dгде а — сторона основания, принадлежащая единовременно плоскости сечения, D — диагональ боковой грани.
5. В произвольной непрямой призме диагональное сечение — параллелограмм, одна сторона которого равна боковому ребру призмы, иная – диагонали основания. Либо сторонами диагонального сечения могут быть диагонали боковых граней и стороны оснований между вершинами призмы, откуда проведены диагонали боковых поверхностей. Площадь параллелограмма S определяется формулой: S=d*hгде d — диагональ основания призмы, h — высота параллелограмма — диагонального сечения призмы.Либо S=a*hгде а — сторона основания призмы, являющаяся и рубежом диагонального сечения, h — высота параллелограмма.
6. Для определения высоты диагонального сечения неудовлетворительно знать линейные размеры призмы. Нужны данные о наклоне призмы к плоскости основания. Последующая задача сводится к ступенчатому решению нескольких треугольников в зависимости от начальных данных об углах между элементами призмы.
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения призмы. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
- Определение призмы
- Элементы призмы
- Варианты сечения призмы
- Виды призм
Определение призмы
Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами.
На рисунке ниже представлен один из самых распространенных видов призмы – четырехугольная прямая (или параллелепипед). Другие разновидности фигуры рассмотрены в последнем разделе данной публикации.
Элементы призмы
Для рисунка выше:
- Основания – равные многоугольники. Это могут быть треугольники, четырех-, пяти-, шестиугольники и т.д. В нашем случае – это параллелограммы (или прямоугольники) ABCD и A1B1C1D1.
- Боковые грани – это параллелограммы: AA1B1B, BB1C1C, CC1D1D и AA1D1D.
- Боковое ребро – отрезок, соединяющий соответствующие друг другу вершины разных оснований (AA1, BB1, CC1 и DD1). Является общей стороной двух боковых граней.
- Высота (h) – это перпендикуляр, проведенный от одного основания к другому, т.е. расстояние между ними. Если боковые ребра расположены под прямым углом к основаниям фигуры, значит они одновременно являются и высотами призмы.
- Диагональ основания – отрезок, который соединяет две противолежащие вершины одного и того же основания (AC, BD, A1C1 и B1D1). У треугольной призмы данного элемента нет.
- Диагональ боковой грани – отрезок, который соединяет две противолежащие вершины одной и той же грани. На рисунке изображены диагонали только одной грани (CD1 и C1D), чтобы не перегружать его.
- Диагональ призмы – отрезок, соединяющий две вершины разных оснований, не принадлежащих одной боковой грани. Мы показали только две из четырех: AC1 и B1D.
- Поверхность призмы – суммарная поверхность двух ее оснований и боковых граней. Формулы для расчета площади поверхности (для правильной фигуры) и объема призмы представлены в отдельных публикациях.
Развёртка призмы – разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований). В качестве примера – для прямоугольной прямой призмы:
Примечание: свойства призмы представлены в отдельной публикации.
Варианты сечения призмы
- Диагональное сечение – секущая плоскость проходит через диагональ основания призмы и два соответствующих боковых ребра.
Примечание: У треугольной призмы нет диагонального сечения, т.к. основанием фигуры является треугольник, у которого нет диагоналей.
- Перпендикулярное сечение – секущая плоскость пересекает все боковые ребра под прямым углом.
Примечание: другие варианты сечения не так распространены, поэтому отдельно на них останавливаться не будем.
Виды призм
Рассмотрим разновидности фигуры с треугольным основанием.
- Прямая призма – боковые грани расположены под прямым углом к основаниям (т.е. перпендикулярны им). Высота такой фигуры равняется ее боковому ребру.
- Наклонная призма – боковые грани фигуры не перпендикулярны ее основаниям.
- Правильная призма – основаниями являются правильные многоугольники. Может быть прямой или наклонной.
- Усеченная призма – часть фигуры, оставшаяся после пересечения ее плоскостью, не параллельной основаниям. Также может быть как прямой, так и наклонной.
На практике часто возникают задачи, которые требуют умения строить сечения геометрических фигур различной формы и находить площади сечений. В данной статье рассмотрим, как строятся важные сечения призмы, пирамиды, конуса и цилиндра, и как рассчитывать их площади.
Объемные фигуры
Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.

Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.
Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).
Цилиндр
Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.

Для этой фигуры существует три важных типа сечения:
- круглое;
- прямоугольное;
- эллиптическое.
Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.
Площадь круглого сечения рассчитывается по формуле:
S1 = pi*r2
Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:
S2 = 2*r*h
Сечения конуса
Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.

Видов конических сечений существует несколько. Перечислим их:
- круглое;
- эллиптическое;
- параболическое;
- гиперболическое;
- треугольное.
Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.
Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:
S1 = pi*r2*z2/h2
Здесь z — это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z < h, то площадь изучаемого сечения будет всегда меньше ее значения для основания.
Треугольное получается, когда плоскость пересекает фигуру по ее оси вращения. Формой получившегося сечения будет равнобедренный треугольник, сторонами которого являются диаметр основания и две образующие конуса. Как находить площадь сечения треугольного? Ответом на этот вопрос будет следующая формула:
S2 = r*h
Это равенство получается, если применить формулу для площади произвольного треугольника через длину его основания и высоту.
Сечения призмы
Призма — это большой класс фигур, которые характеризуются наличием двух одинаковых параллельных друг другу многоугольных оснований, соединенных параллелограммами. Любое сечение призмы — это многоугольник. В виду разнообразия рассматриваемых фигур (наклонные, прямые, n-угольные, правильные, вогнутые призмы) велико и разнообразие их сечений. Далее рассмотрим лишь некоторые частные случаи.

Если секущая плоскость параллельна основанию, то площадь сечения призмы будет равна площади этого основания.
Если плоскость проходит через геометрические центры двух оснований, то есть является параллельной боковым ребрам фигуры, тогда в сечении образуется параллелограмм. В случае прямых и правильных призм рассматриваемый вид сечения будет представлять собой прямоугольник.
Пирамида
Пирамида — это еще один многогранник, который состоит из n-угольника и n треугольников. Пример треугольной пирамиды показан ниже.

Если сечение проводится параллельной n-угольному основанию плоскостью, то его форма будет в точности равна форме основания. Площадь такого сечения вычисляется по формуле:
S1 = So*(h-z)2/h2
Где z — расстояние от основания до плоскости сечения, So — площадь основания.
Если секущая плоскость содержит вершину пирамиды и пересекает ее основание, то мы получим треугольное сечение. Для вычисления его площади необходимо обратиться к использованию соответствующей формулы для треугольника.



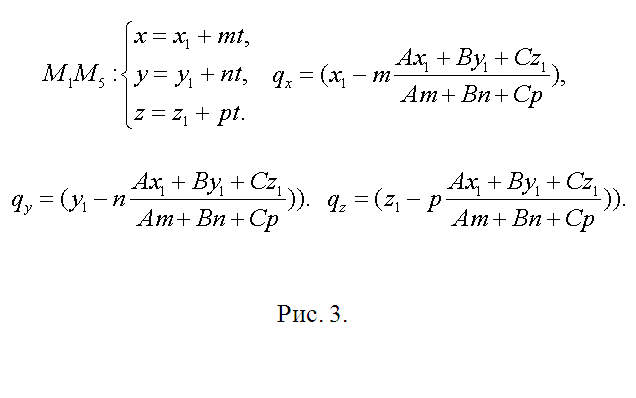
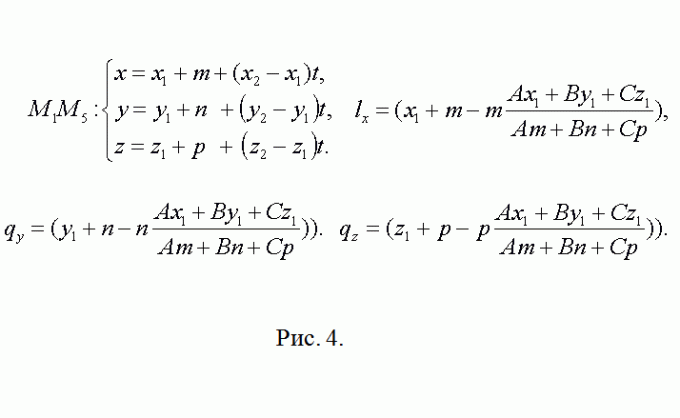
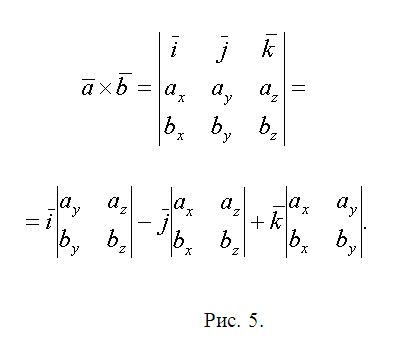



 Примечание: У треугольной призмы нет диагонального сечения, т.к. основанием фигуры является треугольник, у которого нет диагоналей.
Примечание: У треугольной призмы нет диагонального сечения, т.к. основанием фигуры является треугольник, у которого нет диагоналей.



