Как найти площадь сечения прямой призмы плоскостью

q2nr97

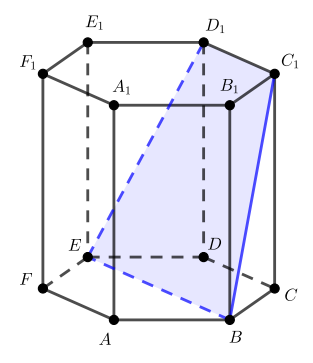
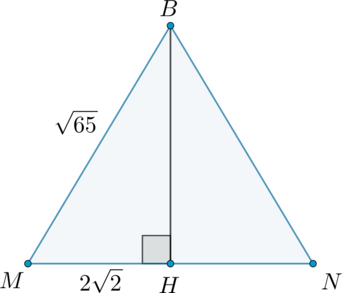
Найди площадь сечения прямой призмы плоскостью (AB1C), если AA1=7, AC=10 и AB=26

zmeura1204

Светило науки — 3376 ответов — 0 раз оказано помощи

Ответ:
125 ед²

Решение:
∆АВС- прямоугольный треугольник
По теореме Пифагора
ВС=√(АВ²-АС²)=√(26²-10²)=
=√(676-100)=√576=24 ед.
ВВ1=АА1=7ед
∆В1ВС- прямоугольный треугольник
По теореме Пифагора
В1С=√(В1В²+ВС²)=√(7²+24²)=
=√(49+576)=√625=25 ед.
ВС перпендикулярно АС, → В1С перпендикулярно АС, Теорема о трех перпендикулярах.
∆АСВ1- прямоугольный треугольник
S(∆ACB1)=½*AC*CB1=10*25/2=
=125 ед²

Источник

7 класс.
Сопоставьте стихотворение Пушкина «Песнь о вещем Олеге» со стихотворением «Конь» из цикла «Песни западных славян». Это стихотворения разных жанров и очень далёких периодов жизни Пушкина – тем интереснее сопоставление. Изложите свои наблюдения в виде мини-сочинения.

«Что ты ржешь, мой конь ретивый,
Что ты шею опустил,
Не потряхиваешь гривой,
Не грызешь своих удил?
Али я тебя не холю?
Али ешь овса не вволю?
Али сбруя не красна?
Аль поводья не шелковы,
Не серебряны подковы,
Не злачены стремена?»

Отвечает конь печальный:
«Оттого я присмирел,
Что я слышу топот дальный,
Трубный звук и пенье стрел;
Оттого я ржу, что в поле
Уж не долго мне гулять,
Проживать в красе и в холе,
Светлой сбруей щеголять;
Что уж скоро враг суровый
Сбрую всю мою возьмет
И серебряны подковы
С легких ног моих сдерет;
Оттого мой дух и ноет,
Что наместо чепрака
Кожей он твоей покроет
Мне вспотевшие бока».

Источник

Тема 13.

Задачи по стереометрии

13

.

12

Нахождение площади сечения

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

задачи по стереометрии

Решаем задачи

Показать ответ и решение

Ответ:

б) √ -- 19-70 7

Показать ответ и решение

Ответ:

7a2√34 ------- 36

Показать ответ и решение

а) Обозначим через α плоскость сечения. Плоскости (B1C1D1 ) и (BCD )
параллельны, следовательно, плоскость α сечет их по параллельным прямым.
Плоскость α пересекает B1C1D1 по прямой D1C1. Докажем, что прямая EB
параллельна D1C1, из этого будет следовать, что она лежит в α, так как
B ∈ α .

Прямые EB ∥ DC в силу правильности шестиугольника ABCDEF, так как в
нем ∘ ∠BED = 60, ∘ ∠EDC = 120 , следовательно, сумма односторонних углов
равна 180∘. Прямые DC ∥D C , 1 1 следовательно, EB ∥ D C . 1 1 Тогда E лежит в
α и ED1C1B — искомое сечение. Кроме того, в четырехугольнике ED1C1B
противолежащие стороны EB и D1C1 параллельны и не равны, следовательно,
ED1C1B — трапеция.

PIC

б) Способ 1.

В правильном шестиугольнике EB = 2DC = 2AB = 20, также по условию
D1C1 = AB = 10. По теореме Пифагора для треугольника BCC1 :

BC = ∘BC2-+-CC2-= √100-+100-=10√2-= ED 1 1 1

Найдем полупериметр трапеции:

√ - √- p= 2⋅10-2+-10+-20= 15+ 10 2 2

Равнобокую трапецию можно вписать в окружность, тогда по формуле
Брахмагупты ее площадь равна

S = ∘ (p−-ED1)(p−-D1C1)(p-− BC1-)(p-− EB-)=

∘ -2-------√---------√--- √- = 15 ⋅(5+ 10 2)(−5+ 10 2)= 75 7

Способ 2.

Введём векторный базис из векторов −A→F =−→a, −B−→C = −→b , −−C→C1 = −→c. Длины
этих векторов a =b = c= 10. Из определения правильной призмы −→a ⊥ −→c
и −→ −→ b ⊥ c , а поскольку шестиугольник ABCDEF — правильный, то
прямые AF и BC образуют угол ∘ 60. Тогда можно посчитать скалярное
произведение:

(−→a,−→b )= a⋅b⋅cos60∘ = 10⋅10⋅0,5 = 50 −→ −→ ∘ (a, c)= a⋅c⋅cos90 = 0 (−→b ,−→c)= b⋅c⋅cos90∘ = 0

PIC

В пункте а) было ранее доказано, что EBC1D1 — трапеция. По свойствам
правильного шестиугольника диагональ BE = 2a. Тогда для определения
площади сечения можно сначала посчитать площадь треугольника EBC1, после
чего домножить её на 1,5, поскольку площадь EC1D1 составляет половину от
площади EBC1. Выразим векторы BE и BC1 через базисные вектора и найдём
квадраты длин:

−−→ −→ BE =2AF =2−→a −−→ −−→ −−→ −→ −→ BC1 = BC + CC1 = b + c BE2 = (2a)2 = 4a2 = 202 −→ −→ 2 −→ −→ 2 −→ −→ 2 −→ −→ 2 2 2 2 BC1 = (b , c) = (b , b ) +( c,c) − 2(b , c)= b + c = 2a =2 ⋅10

Таким образом,

1 1 ∘------------- SEBC1 = 2BE ⋅BC1 sin ∠EBC1 = 2BEBC1 1 − cos2∠EBC1 = ∘ --------------------------- ∘------------------- = 1 BE2BC21 − BE2BC21 cos2∠EBC1 = 1 BE2BC21 − (−B−→E, −B−C→1)2 = 2 ∘ ----------------- ∘ ---2------------------ = 1 8a4− (2−→a,−→b + −→c )2 = 1 8a4 − 4(−→a ,−→b )2− 4(−→a,−→c)2 = 2 ∘ ---------------2-- = 1 2⋅2002− 4⋅502− 2⋅0= 1 ⋅100√8-−-1= 50√7 2 2

Тогда площадь трапеции равна

√- SEBC1D1 = 1,5SEBC1 = 75 7

Ответ:

б) √ - 75 7

Критерии оценки

Содержание критерия

Балл

Имеется верное доказательство
утверждения пункта а) и обоснованно
получен верный ответ в пункте б)

3

Обоснованно получен верный ответ в
пункте б)

2

ИЛИ

имеется верное
доказательство утверждения пункта
а) и при обоснованном решении
пункта б) получен неверный ответ
из-за арифметической ошибки

Имеется верное доказательство
утверждения пункта а)

1

ИЛИ

при обоснованном решении пункта
б) получен неверный ответ из-за
арифметической ошибки

ИЛИ

обоснованно получен верный ответ в
пункте б) с
использованием утверждения пункта
а), при этом пункт а) не выполнен

Решение не соответствует ни одному
из критериев, перечисленных выше

0

Максимальный балл

3

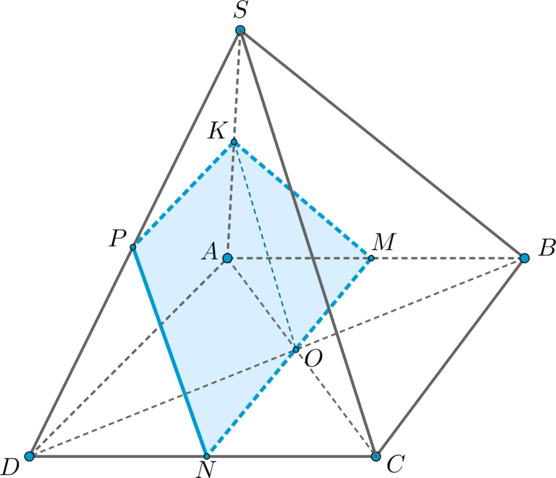
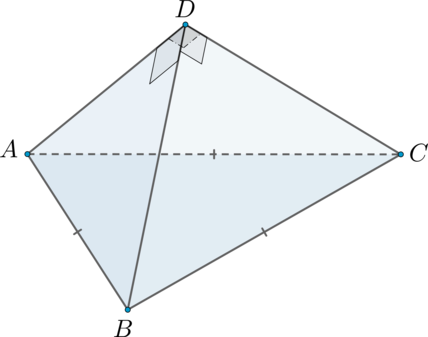
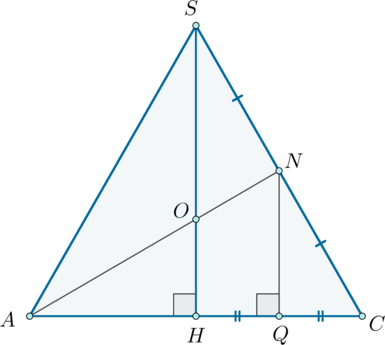
Правильная треугольная пирамида рассечена плоскостью, перпендикулярной основанию и делящей две стороны
основания пополам. Найдите площадь сечения пирамиды этой плоскостью, если известно, что сторона основания равна
2 , а высота пирамиды равна 4 .

Показать ответ и решение

Ответ:

1,5

Показать ответ и решение

1) Пусть AC ∩ BD = O . Две плоскости параллельны, если две пересекающиеся прямые одной
плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

 PIC

 Заметим, что т.к. ∠SAB = ∠SAD = 90 ∘ ⇒ SA ⊥ (ABC ) .

Проведем в плоскости SAC прямую OK ∥ SC . Т.к. O – середина AC , то по теореме Фалеса K
– середина SA . Через точку K в плоскости SAB проведем KM ∥ SB (следовательно, M –
середина AB ). Таким образом, плоскость, проходящая через прямые OK и KM , и будет искомой
плоскостью.

Необходимо найти сечение пирамиды этой плоскостью. Соединив точки O и M , получим прямую
M N .

Т.к. α ∥ (SBC ) ,то α пересечет плоскость SCD по прямой N P ∥ SC (если N P ∩ SC ⁄= ∅ , то
α ∩ (SBC ) ⁄= ∅ , что невозможно ввиду их параллельности).

Таким образом, KM N P – искомое сечение, причем KP ∥ AD ∥ M N ⇒ это трапеция.

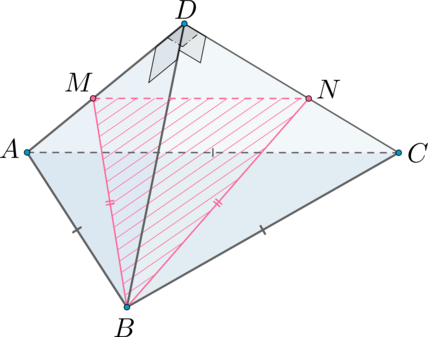
2) Т.к. все точки K, M, N, P – середины отрезков SA, AB, CD, SD соответственно,
то:

а) M N = AD = a

б) KP = 1-AD = a- 2 2

в) √ -- KM = 1SB = a--2- 2 2

Заметим, что по теореме о трех перпендикулярах SB ⊥ BC ⇒ KM ⊥ M N . Таким образом,
KM N P – прямоугольная трапеция.

√ -- KP---+-M-N-- 3--2-2 SKMNP = 2 ⋅ KM = 8 a

Ответ:

1) Рисунок.

2) √ -- 3 2 2 ----a 8

Показать ответ и решение

б) По теореме Менелая для △ADC и прямой QK имеем:

AN-- ⋅ DK- ⋅ CQ-= 1 ⇒ QA = 8 N D KC QA

По условию AM = 13AB = 8 . Т.к. QA = AM и ∠CAB = 60∘ ⇒ ∠AQM = 30∘ . Следовательно,
∠BM T = 30∘ , тогда ∠M T B = 90∘ . Следовательно, BT = 8 . Заметим, что △N DK = △M BT по
углу и двум прилежащим сторонам, следовательно, M T = N K . Также заметим, что так как
BT = DK = 8 , то TK ∥ DB . Также и M N ∥ DB . Следовательно, M N KT – равнобедренная
трапеция.

Основания M N = 8 , KT = 16 , по теореме Пифагора √ -------- √ -- M T = 162 − 82 = 8 3 . Следовательно,
если провести высоту M H , то T H = 0,5(16 − 8) = 4 . Тогда по теореме Пифагора
∘ --√--------- √ --- M H = (8 3)2 − 42 = 4 11 . Следовательно,

8-+-16- √ --- √ --- SMNKT = 2 ⋅ 4 11 = 48 11

Ответ:

б) √ --- 48 11

Показать ответ и решение

а) Для того, чтобы доказать, что пирамида является правильной, нужно доказать, что в основании
пирамиды находится правильный многоугольник, а боковые ребра равны.
PIC
Возьмем за основание △ABC – он правильный по условию.
Осталось доказать, что DA = DC = DB .
Рассмотрим △ADB и △CDB . Они прямоугольные и равны по катету и гипотенузе. Следовательно,
DA = DC . Аналогично рассматривая другие боковые грани, доказываем, что DA = DB .
Следовательно, DA = DB = DC , чтд.

б) Заметим, что так как DM : M A = DN : N C = 4 : 3 и боковые грани – равные треугольники, то
BM = BN . PIC
Так как DM : M A = DN : N C = 4 : 3 , то по теореме Фалеса M N ∥ AC , также △DM N ∼ △DAC .
Из подобия следует:

M N DM 4 4 √ -- -----= -----= -- → M N = -AC = 4 2 AC DA 7 7

Найдем BM .
Так как △ADB прямоугольный и равнобедренный, то √ -- DA = DB = AB : 2 , следовательно,
DA = 7 .
Рассмотрим прямоугольный △DM B . Так как 4 DM = 7DA = 4 , то √ -2---2- √ --- BM = 4 + 7 = 65 .
Рассмотрим теперь △BM N : PIC
Так как он равнобедренный, то высота BH , проведенная к основанию, будет также и медианой.
Следовательно,

√ ------- √ --- BH = 65 − 8 = 57

Таким образом,

1 √ ---- S△BMN = --⋅ BH ⋅ M N = 2 114 2

Ответ:

б) √ ---- 2 114

Дана правильная четырехугольная пирамида SABCD с вершиной S , стороны основания которой
равны √ -- 6 2 , а боковые ребра равны 21 .

а) Постройте сечение пирамиды плоскостью, проходящей через точку A и середину ребра SC
параллельно прямой BD .

б) Найдите площадь построенного сечения.

Показать ответ и решение

б) Заметим, что по теореме о трех перпендикулярах (так как OH ⊥ (ABC ),AH ⊥ BD )
AO ⊥ BD . Так как BD ∥ M K , то AO ⊥ M K , следовательно, AN ⊥ M K . Следовательно, у
четырехугольника AM N K диагонали взаимно перпендикулярны. Значит, его площадь можно найти
как

S = 1AN ⋅ M K. 2

Заметим сразу, что √ -- BD = AC = AB 2 = 12 .
Рассмотрим плоскость ASC .

 PIC

 По теореме Менелая:

-SN- ⋅-CA- ⋅ HO- = 1 ⇒ HO--= 1- ⇒ OS = 2OH ⇒ SO--= 2. N C AH OS OS 2 SH 3

(это
нам понадобится позже для поиска M K )

 Проведем N Q ⊥ AC . Тогда из подобия △SHC и △N QC :

√ ------------ √-------- √ ------ SH-- = SC--= 2 ⇒ N Q = 1SH = 1- SC2 − HC2 = 1- 212 − 62 = 1- 81 ⋅ 5 N Q N C 2 2 2 2

Q –
середина HC , следовательно, 3 3 AQ = 4AC = 4 ⋅ 12 = 9 . Тогда по теореме Пифагора

∘ ------------ ∘ ----------- AN = AQ2 + N Q2 = 81-⋅ 5-+ 81 = 27-. 4 2

Рассмотрим BSD . Так как △M SK ∼ △BSD , то

M K SO 2 2 2 -----= ----= -- ⇒ M K = -BD = --⋅ 12 = 8. BD SH 3 3 3

Следовательно, площадь сечения равна

S = 1-⋅ 8 ⋅ 27-= 54. 2 2

Показать ответ и решение

1) ПустьK – середина AC , SX, AL – медианы грани ASB , CL, SY – медианы грани CSB ,
AL ∩ SX = M, CL ∩ SY = N . SO – высота пирамиды.

Найдем сечение пирамиды плоскостью M N K .
Т.к. пирамида правильная, то △SXY – равнобедренный, 2 SM = SN = -SX ⇒ M N ∥ XY ⇒ M N ∥ (ABC ) 3 .
Таким образом, плоскость M N K содержит прямую M N , параллельную ABC , следовательно,
плоскость M N K пересечет плоскость ABC по прямой, параллельной M N (если это не так, то линия
пересечения этих плоскостей l ∩ M N = E ⇒ E ∈ (ABC ) и E ∈ M N ⇒ M N не может быть
параллельна (ABC ) ).

PIC

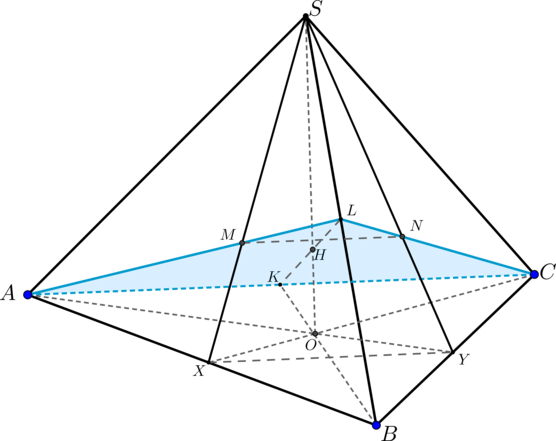
Прямая, проходящая через точку K и параллельная M N (или XY ) – это AC . Следовательно,
сечением является равнобедренный треугольник ALC .

2) Пусть LK ∩ SO = H . Тогда по теореме о трех перпендикулярах HK ⊥ AC как наклонная
(HO ⊥ (ABC ),OK ⊥ AC как проекция). Следовательно, и LK ⊥ AC .

Тогда 1- SALC = 2AC ⋅ LK .

PIC

Рассмотрим √ -- √ -- √ -- △SKB : BK = AB ⋅--3-= 21--3-⇒ cosB = -7√-3- 2 2 12 2 .

Тогда по теореме косинусов для △KLB :

2 729- 27- KL = 4 ⇒ KL = 2

Значит, SALC = 567- 4 .

Ответ:

567 ---- 4 .

Показать ответ и решение

а) 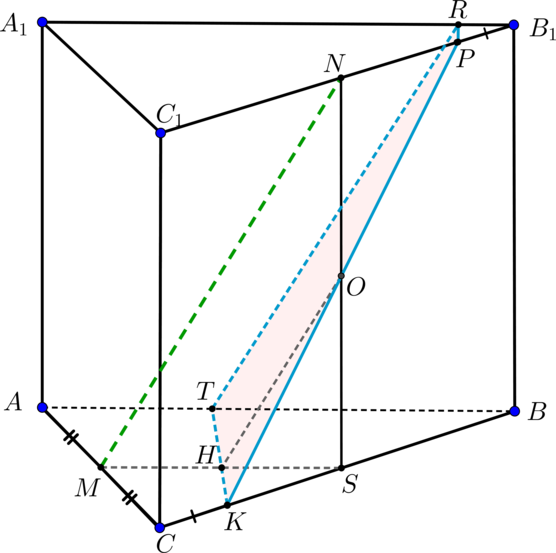PIC

Если прямая M N ∥ α ⇒ M N параллельна некоторой прямой, лежащей в α . Проведем
N S ⊥ BC, N S ∩ KP = O . В плоскости M N S проведем OH ∥ M N ⇒ M H = HS . Тогда прямая
KH ∩ AB = T . Так как плоскости ABC и A1B1C1 параллельны, то α пересечет плоскость A1B1C1
по прямой, параллельной KT . Следовательно, проведем P R ∥ KT . Таким образом, TRP K – искомое
сечение (трапеция).

б) Заметим, что 1 5 CK = --⋅ 15 =--⇒ KS = 5 6 2 . Т.к. M S – средняя линия треугольника
ABC ⇒ M S = 8 ⇒ HS = 4 . Так как ∠HSK = ∠ABC , то по теореме косинусов
∘ -------------------- HK = 16 + 25 − 2 ⋅ 4 ⋅ 5 ⋅ 45 = 3 . Таким образом, по обратной теореме Пифагора треугольник HKS –
прямоугольный, следовательно, ∠H = 90 ∘ . Таким образом, по теореме о трех перпендикулярах, из
того, что N S ⊥ (ABC ),HS ⊥ KT ⇒ OH ⊥ KT .

Найдем основания трапеции KT и P R .

sin ∠KSH = 3-= sin ∠B = KT-- ⇒ KT = 15- 5 KB 2 .

3 △ PRB1 ∼ △KT B ⇒ P R = -- 2 .

Таким образом, ( ) 1- 15- 3- √ -- √ -- STRP K = 2 ⋅ 2 + 2 ⋅ 8 2 = 36 2

Ответ:

б) √ -- 36 2

Показать ответ и решение

а) 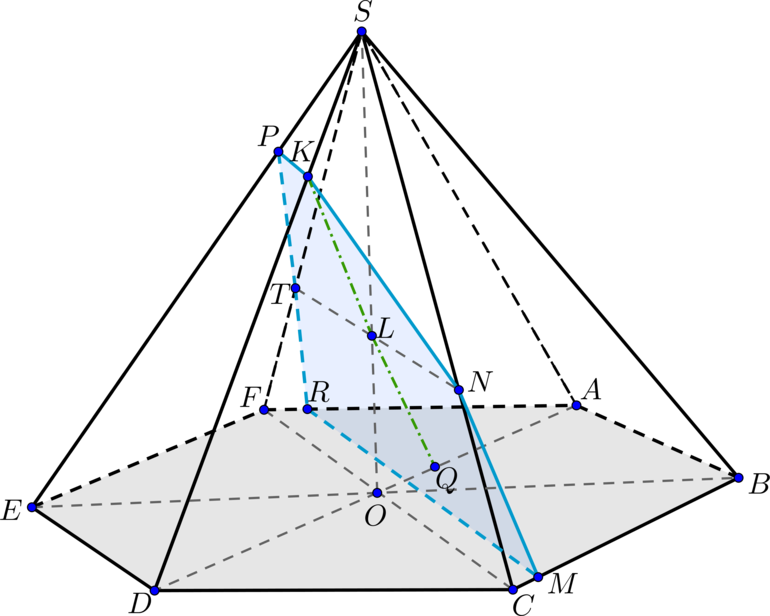PIC

Две плоскости параллельны, если две пересекающиеся прямые из одной плоскости будут
параллельны некоторых двум пересекающимся прямым из другой плоскости.Проведем через точку L
прямые, параллельные AB и AS .
Из свойства правильного шестиугольника следует, что F C ∥ AB . Проведем в плоскости F SC через
точку L : T N ∥ F C .

Тогда по теореме Фалеса SN ST SL 3 ----= ----= ----= -- N C TF LO 1

В плоскости ASD проведем через точку L : KQ ∥ SA .

Из теоремы Фалеса следует, что AQ SL 3 ----= ----= -- QO LO 1

Пусть AQ = 3x,QO = x . Из свойств правильного шестиугольника следует, что DO = OA = 4x .

Тогда по теореме Фалеса DQ--= DK-- = 5x-= 5- QA KS 3x 3

б) Достроим сечение пирамиды плоскостью α . Плоскость α пересечет плоскость основания по
прямой RM ∥ AB, Q ∈ RM . Значит, BM--- AR-- 3- M C = RF = 1

Найдем все их стороны.
Из подобия 3 3 △ ST N ∼ △SF C ⇒ TN = -F C = -a = 6 4 2
Из подобия △ CN M ∼ △CSB ⇒ N M = 1-b = 7- 4 4

Достроим трапецию F ABC до треугольника F W C – он правильный. 7 7 ⇒ RM = -F C = -a = 7 8 4
Из подобия 3 3 3 △ SP K ∼ △SED ⇒ P K = -ED = --a = -- 8 8 2

Найдем KN из грани SCD :
По теореме косинусов 2b2 − a2 cos∠S = -----2-- 2b .

В △ KSN : 3- 3- KN = 8b,SN = 4b ⇒ по теореме косинусов 2 -9- 2 2 27- KN = 64 ⋅ (b + 2a ) ⇒ KN = 8

Обозначим высоту трапеции M N T R за h1 . Тогда ∘ -------- 49- 1- 3-√ -- h1 = 16 − 4 = 4 5

Высота трапеции N KP T h = ∘ -272−--81-= 9√5-- 1 64 16 8

Тогда площадь сечения ( ) √-- √-- √ -- S = 1-⋅ 3-+ 6 ⋅ 9 5 + 1⋅ (6 + 7) ⋅ 3 5 = 291--5- 2 2 8 2 4 32

Ответ:

б) √-- 291--5- 32

Источник

Ответ:
125 ед²

Решение:
∆АВС- прямоугольный треугольник
По теореме Пифагора
ВС=√(АВ²-АС²)=√(26²-10²)=
=√(676-100)=√576=24 ед.
ВВ1=АА1=7ед
∆В1ВС- прямоугольный треугольник
По теореме Пифагора
В1С=√(В1В²+ВС²)=√(7²+24²)=
=√(49+576)=√625=25 ед.
ВС перпендикулярно АС, → В1С перпендикулярно АС, Теорема о трех перпендикулярах.
∆АСВ1- прямоугольный треугольник
S(∆ACB1)=½*AC*CB1=10*25/2=
=125 ед²

Источник

Как найти площадь сечения призмы

Призма — это многогранник, основанием которого служат равные многоугольники, боковыми гранями — параллелограммы. Для того чтобы найти площадь сечения призмы, необходимо знать, какое сечение рассматривается в задании. Различают перпендикулярное и диагональное сечение.

Как найти площадь сечения призмы

Инструкция

Способ расчета площади сечения также зависит от данных, которые уже имеются в задаче. Кроме этого, решение определяется тем, что лежит в основании призмы. Если необходимо найти диагональное сечение призмы, найдите длину диагонали, которая равна корню из суммы (основания сторон в квадрате). Например, если основания сторон прямоугольника равны 3 см и 4 см, соответственно, длина диагонали равна корню из (4х4+3х3)= 5 см. Площадь диагонального сечения найдите по формуле: диагональ основания умножить на высоту.

Если в основании призмы находится треугольник, для вычисления площади сечения призмы используйте формулу: 1/2 часть основания треугольника умножить на высоту.

В случае, если в основании находится круг, площадь сечения призмы найдите умножением числа «пи» на радиус заданной фигуры в квадрате.

Различают следующие виды призм — правильные и прямые. Если необходимо найти сечение правильной призмы, вам нужно знать длину только одной из сторон многоугольника, ведь в основании лежит квадрат, у которого все стороны равны. Найдите диагональ квадрата, которая равна произведению его стороны на корень из двух. После этого перемножив диагональ и высоту, вы получите площадь сечения правильной призмы.

Призма имеет свои свойства. Так, площадь боковой поверхности произвольной призмы вычисляется по формуле, где — периметр перпендикулярного сечения, — длина бокового ребра. При этом перпендикулярное сечение перпендикулярно ко всем боковым ребрам призмы, а его углы — это линейные углы двугранных углов при соответствующих боковых ребрах. Перпендикулярное сечение перпендикулярно и ко всем боковым граням.

Источники:

  • диагональное сечение призмы

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти голосовое устройство
  • Генеалогическая таблица как составить
  • Как исправить ошибку на телефоне com android phone
  • Как найти максимальное количество подсетей
  • Как составить финансовую заявку на