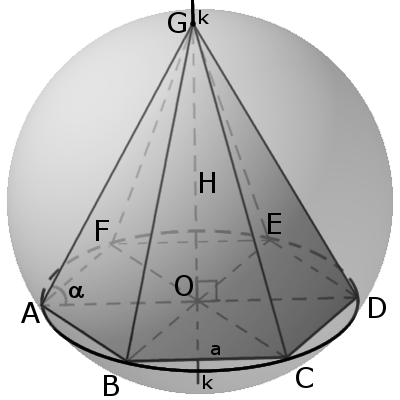
Основанием пирамиды SABCD служит прямоугольник ABCD, диагональ BD которого составляет со стороной BC угол α. Все боковые ребра пирамиды имеют длину l, а величина угла ASC равна 2β. Пирамида пересечена плоскостью, равноудаленной от всех ее вершин. Определить площадь сечения пирамиды этой плоскостью.
Непонятно, что вызвало трудности в этой задаче. Тут ведь всё непосредственно дано. Из треугольника ASC находим диагональ основания. Далее — его стороны и площадь. Сечение проходит посередине, его площадь в 4 раза меньше площади основания.
Площадь сечения пирамиды
Пирамида — это многогранник, основанием которого является произвольный многоугольник, а боковые грани являются треугольниками, имеющие общую вершину. Основными математическими характеристиками пирамиды являются площадь основания и высота.
Сечение пирамиды — это изображение фигуры, образованной рассечением пирамиды плоскостью в поперечном или продольном направлении.
Формула для расчета площади основания пирамиды или сечения параллельного основанию:
S = a 2 , где
a — размер основания или сечения пирамиды.
Формула для расчета площади диагонального сечения пирамиды:
S = a * h / 2, где
a — основание пирамиды;
h — высота пирамиды.
Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета площади основания, бокового и диагонального сечения пирамиды, если известны основание пирамиды и высота правильной четырехугольной пирамиды. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения пирамиды (площадь диагонального сечения пирамиды, площадь бокового сечения пирамиды, площадь основания пирамиды и площадь сечения пирамиды параллельного основанию).
Как определить площадь сечения цилиндра, конуса, призмы и пирамиды? Формулы
На практике часто возникают задачи, которые требуют умения строить сечения геометрических фигур различной формы и находить площади сечений. В данной статье рассмотрим, как строятся важные сечения призмы, пирамиды, конуса и цилиндра, и как рассчитывать их площади.
Объемные фигуры
Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.

Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.
Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).
Цилиндр
Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.
Для этой фигуры существует три важных типа сечения:
- круглое;
- прямоугольное;
- эллиптическое.
Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.
Площадь круглого сечения рассчитывается по формуле:
Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:
Сечения конуса
Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.
Видов конических сечений существует несколько. Перечислим их:
- круглое;
- эллиптическое;
- параболическое;
- гиперболическое;
- треугольное.
Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.
Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:
Здесь z — это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z Понравилась статья? Поделись с друзьями:
Пирамида. Формулы и свойства пирамиды
Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
- Альфашкола
- Статьи
- Площадь прямоугольной пирамиды
Площадь прямоугольной пирамиды
Дарим в подарок бесплатный вводный урок!
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Репетитор по алгебре
- Репетитор по английскому языку для подготовки к ЕГЭ
- Репетитор по английскому языку для подготовки к ОГЭ
- Подготовка к олимпиадам по английскому языку
- Репетитор по английскому для взрослых
- Репетитор для подготовки к ЕГЭ по истории
- Репетитор для подготовки к ВПР по русскому языку
- Репетитор по биологии для подготовки к ЕГЭ
- Репетитор по географии для подготовки к ОГЭ
Для того чтобы найти площадь всей поверхности прямоугольной пирамиды применим формулу:
(S= a^2+ 2asqrt{b^2−frac{a^2}{4}} )
Сторона основания a :
Сторона b :
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Светлана Валентиновна Емец
Репетитор по математике
Стаж (лет)
19
Образование:
Государственное образовательное учреждение высшего профессионального образования «Самарский государственный педагогический университет»
Проведенных занятий:
137
Форма обучения:
Дистанционно (Скайп)
Сергей Андреевич Селяев
Репетитор по математике
Стаж (лет)
4
Образование:
Санкт-Петербургский государственный университет аэрокосмического приборостроения
Проведенных занятий:
1982
Форма обучения:
Дистанционно (Скайп)
Иван Николаевич Лукашин
Репетитор по математике
Стаж (лет)
8
Образование:
Тульский Государственный Университет
Проведенных занятий:
179
Форма обучения:
Дистанционно (Скайп)
Похожие статьи
- Значение синуса, косинуса и тангенса 30°, 45° и 60°
- Положительное и отрицательное направление угла
- МИФИ: Бизнес-Информатика
- РУДН: факультет ветеринарии
- ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 2)
- ЕГЭ по математике, базовый уровень. Преобразование алгебраических выражений
- Решаем профильный ЕГЭ. Простейшие текстовые задачи
- Как осилить список литературы для внеклассного чтения на каникулах и стоит ли это вообще делать?
Решим задачу из Задания С2 для подготовки к ЕГЭ по математике:
На ребре 








Точки 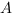

Точка 

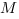

Проведем через точку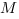


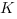



Через пересекающиеся прямые 


2. Найдем площадь четырехугольника 
Докажем, что его диагонали перпендикулярны. Опустим перпендикуляр из точки 









Найдем диагонали нашего сечения.


По теореме Пифагора из прямоугольного треугольника
Чтобы найти длину отрезка 
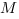


Проведем через точку 



Треугольник 




Теперь рассмотрим подобные треугольники 


Рассмотрим треугольник 


Треугольник 
Следовательно,
Итак,
Ответ: 35
И.В. Фельдман, репетитор по математике.
Определение
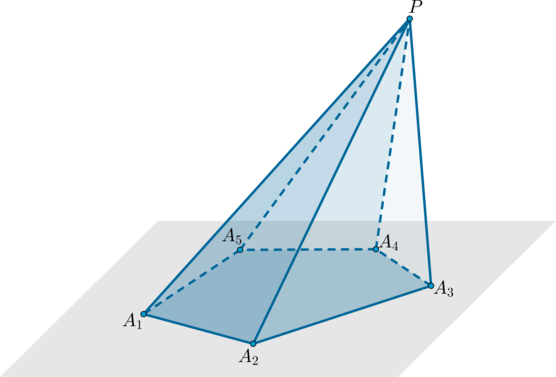
Пирамида – это многогранник, составленный из многоугольника (A_1A_2…A_n) и (n) треугольников с общей вершиной (P) (не лежащей в плоскости многоугольника) и противолежащими ей сторонами, совпадающими со сторонами многоугольника.
Обозначение: (PA_1A_2…A_n).
Пример: пятиугольная пирамида (PA_1A_2A_3A_4A_5).
Треугольники (PA_1A_2, PA_2A_3) и т.д. называются боковыми гранями пирамиды, отрезки (PA_1, PA_2) и т.д. – боковыми ребрами, многоугольник (A_1A_2A_3A_4A_5) – основанием, точка (P) – вершиной.
Высота пирамиды – это перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Пирамида, в основании которой лежит треугольник, называется тетраэдром.
Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено одно из условий:
((a)) боковые ребра пирамиды равны;
((b)) высота пирамиды проходит через центр описанной около основания окружности;
((c)) боковые ребра наклонены к плоскости основания под одинаковым углом.
((d)) боковые грани наклонены к плоскости основания под одинаковым углом.
Правильный тетраэдр – это треугольная пирамида, все грани которой – равные равносторонние треугольники.
Теорема
Условия ((a), (b), (c), (d)) эквивалентны.
Доказательство
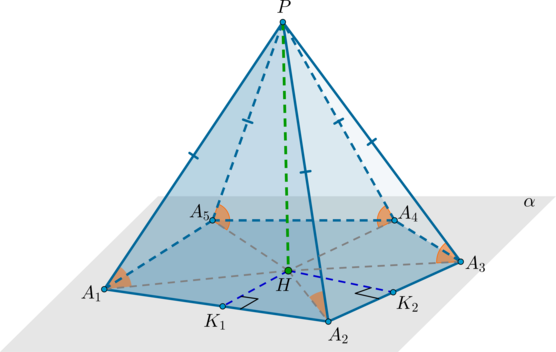
Проведем высоту пирамиды (PH). Пусть (alpha) – плоскость основания пирамиды.
1) Докажем, что из ((a)) следует ((b)). Пусть (PA_1=PA_2=PA_3=…=PA_n).
Т.к. (PHperp alpha), то (PH) перпендикулярна любой прямой, лежащей в этой плоскости, значит, треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) – прямоугольные. Значит, эти треугольники равны по общему катету (PH) и гипотенузам (PA_1=PA_2=PA_3=…=PA_n). Значит, (A_1H=A_2H=…=A_nH). Значит, точки (A_1, A_2, …, A_n) находятся на одинаковом расстоянии от точки (H), следовательно, лежат на одной окружности с радиусом (A_1H). Эта окружность по определению и есть описанная около многоугольника (A_1A_2…A_n).
2) Докажем, что из ((b)) следует ((c)).
Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) прямоугольные и равны по двум катетам. Значит, равны и их углы, следовательно, (angle PA_1H=angle PA_2H=…=angle PA_nH).
3) Докажем, что из ((c)) следует ((a)).
Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) прямоугольные и по катету и острому углу. Значит, равны и их гипотенузы, то есть (PA_1=PA_2=PA_3=…=PA_n).
4) Докажем, что из ((b)) следует ((d)).
Т.к. в правильном многоугольнике совпадают центры описанной и вписанной окружности (вообще говоря, эта точка называется центром правильного многоугольника), то (H) – центр вписанной окружности. Проведем перпендикуляры из точки (H) на стороны основания: (HK_1,
HK_2) и т.д. Это – радиусы вписанной окружности (по определению). Тогда по ТТП ((PH) – перпендикуляр на плоскость, (HK_1, HK_2) и т.д. – проекции, перпендикулярные сторонам) наклонные (PK_1, PK_2) и т.д. перпендикулярны сторонам (A_1A_2, A_2A_3) и т.д. соответственно. Значит, по определению (angle PK_1H, angle PK_2H) равны углам между боковыми гранями и основанием. Т.к. треугольники (PK_1H, PK_2H, …) равны (как прямоугольные по двум катетам), то и углы (angle PK_1H, angle PK_2H, …) равны.
5) Докажем, что из ((d)) следует ((b)).
Аналогично четвертому пункту треугольники (PK_1H, PK_2H, …) равны (как прямоугольные по катету и острому углу), значит, равны отрезки (HK_1=HK_2=…=HK_n). Значит, по определению, (H) – центр вписанной в основание окружности. Но т.к. у правильных многоугольников центры вписанной и описанной окружности совпадают, то (H) – центр описанной окружности. Чтд.
Следствие
Боковые грани правильной пирамиды – равные равнобедренные треугольники.
Определение
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Апофемы всех боковых граней правильной пирамиды равны между собой и являются также медианами и биссектрисами.
Важные замечания
1. Высота правильной треугольной пирамиды падает в точку пересечения высот (или биссектрис, или медиан) основания (основание – правильный треугольник).
2. Высота правильной четырехугольной пирамиды падает в точку пересечения диагоналей основания (основание – квадрат).
3. Высота правильной шестиугольной пирамиды падает в точку пересечения диагоналей основания (основание – правильный шестиугольник).
4. Высота пирамиды перпендикулярна любой прямой, лежащей в основании.
Определение
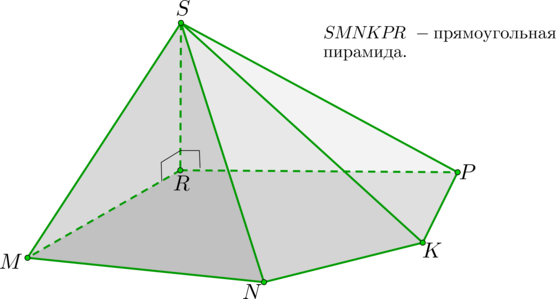
Пирамида называется прямоугольной, если одно ее боковое ребро перпендикулярно плоскости основания.
Важные замечания
1. У прямоугольной пирамиды ребро, перпендикулярное основанию, является высотой пирамиды. То есть (SR) – высота.
2. Т.к. (SR) перпендикулярно любой прямой из основания, то (triangle SRM, triangle SRP) – прямоугольные треугольники.
3. Треугольники (triangle SRN, triangle SRK) – тоже прямоугольные.
То есть любой треугольник, образованный этим ребром и диагональю, выходящей из вершины этого ребра, лежащей в основании, будет прямоугольным.
[{Large{text{Объем и площадь поверхности пирамиды}}}]
Теорема
Объем пирамиды равен трети произведения площади основания на высоту пирамиды: [V_{text{пирамиды}}=dfrac13 S_{text{осн}}cdot h]
Следствия
Пусть (a) – сторона основания, (h) – высота пирамиды.
1. Объем правильной треугольной пирамиды равен (V_{text{прав.треуг.пир.}}=dfrac{sqrt3}{12}a^2h),
2. Объем правильной четырехугольной пирамиды равен (V_{text{прав.четыр.пир.}}=dfrac13a^2h).
3. Объем правильной шестиугольной пирамиды равен (V_{text{прав.шест.пир.}}=dfrac{sqrt3}{2}a^2h).
4. Объем правильного тетраэдра равен (V_{text{прав.тетр.}}=dfrac{sqrt3}{12}a^3).
Теорема
Площадь боковой поверхности правильной пирамиды равна полупроизведению периметра основания на апофему.
[{Large{text{Усеченная пирамида}}}]
Определение
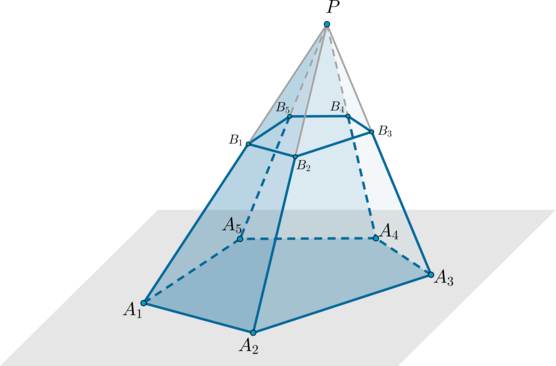
Рассмотрим произвольную пирамиду (PA_1A_2A_3…A_n). Проведем через некоторую точку, лежащую на боковом ребре пирамиды, плоскость параллельно основанию пирамиды. Данная плоскость разобьет пирамиду на два многогранника, один из которых – пирамида ((PB_1B_2…B_n)), а другой называется усеченная пирамида ((A_1A_2…A_nB_1B_2…B_n)).
Усеченная пирамида имеет два основания – многоугольники (A_1A_2…A_n) и (B_1B_2…B_n), которые подобны друг другу.
Высота усеченной пирамиды – это перпендикуляр, проведенный из какой-нибудь точки верхнего основания к плоскости нижнего основания.
Важные замечания
1. Все боковые грани усеченной пирамиды – трапеции.
2. Отрезок, соединяющий центры оснований правильной усеченной пирамиды (то есть пирамиды, полученной сечением правильной пирамиды), является высотой.