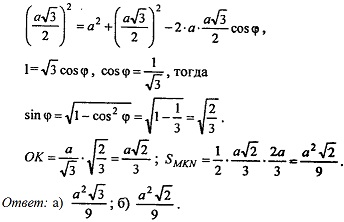Как найти площадь сечения тетраэдра треугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Тетраэдр. Построение сечений тетраэдра

План урока

Тетраэдр;
Построение сечений тетраэдра.

Цели урока

Знать, что такое тетраэдр и как называются его элементы;
Знать, что понимают под сечением тетраэдра;
Уметь строить сечения тетраэдров.

Разминка

Какая фигура на плоскости называется многоугольником?
Что представляет собой множество всех общих точек двух различных непараллельных плоскостей?
Две параллельные плоскости пересечены третьей (секущей) плоскостью. Что можно сказать о взаимном расположении прямых по которым секущая плоскость пересекает данные параллельные плоскости?
Боковые стороны трапеции параллельны плоскости α. Параллельны ли плоскость α и плоскость трапеции?
Прямая a пересекает плоскость α. Лежит ли в плоскости α хоть одна прямая, параллельная прямой α?

Рис. 1. Тетраэдр

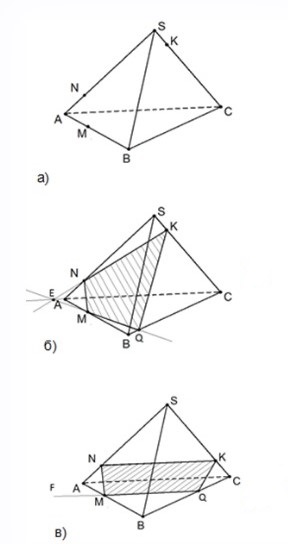
Рассмотрим произвольный треугольник ABC и точку S, не лежащую в плоскости этого треугольника (рис. 1). Соединим точку S отрезками с вершинами треугольника ABC. В результате получим треугольники SAB, SBC, SCA. Пространственная фигура, состоящая из треугольников ABC, SAB, SBC, SCA называется тетраэдром и обозначается SABC.

Тетраэдр является разновидностью многогранников, которым будет посвящена одна из глав курса стереометрии.

Определение 1

Тетраэдр
– это многогранник, состоящий из треугольника, точки не лежащий в плоскости этого треугольника и трёх отрезков соединяющих данную точку с вершинами данного треугольника.

Треугольники, из которых состоит тетраэдр, называются
гранями
тетраэдра.

Стороны этих треугольников называются
рёбрами
тетраэдра.

Вершины этих треугольников называются
вершинами
тетраэдра.

Определение 2

Тетраэдр, у которого все грани — равносторонние треугольники, называется
правильным
.

Таким образом, тетраэдр SABC (как и любой другой тетраэдр) имеет четыре грани (ABC, SAB, SBC, SCA), шесть рёбер (AB, BC, AC, SA, SB, SC) и четыре вершины (S, A, B, C). Два ребра тетраэдра, не имеющие общих вершин, называют противоположными. На рисунке 1 парами противоположных рёбер являются SA и BC, SB и AC, SC и AB. Одну из граней можно рассматривать как основание тетраэдра. В этом случае остальные грани называют боковыми.

Упражнение 1

Изобразите треугольник MNK и точку E, не лежащую в плоскости этого треугольника. Соедините отрезками точку E с вершинами треугольника MNK.

а) Запишите обозначение тетраэдра, изображённого на полученном рисунке, а также все грани, рёбра и вершины этого тетраэдра.

б) Запишите пары противоположных рёбер этого тетраэдра.

Построение сечений тетраэдра

При решении многих стереометрических задач, связанных с тетраэдром, важно уметь строить на рисунке их сечения различными плоскостями. Разберём что называют сечением тетраэдра.

Определение 3

Секущая плоскость тетраэдра
– это плоскость по обе стороны от которой имеются точки данного тетраэдра.

Секущая плоскость тетраэдра пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки представляет собой сечение тетраэдра.

Определение 4

Сечение тетраэдра
—многоугольник, образованный пересечением плоскости с данным тетраэдром.

Тетраэдр имеет четыре грани, значит сечение тетраэдра не может иметь более четырёх сторон. Следовательно, сечением тетраэдра могут быть только треугольники и четырёхугольники.

Рассмотрим примеры построения различных сечений тетраэдра.

Рис. 2. К примеру 1

Пример 1

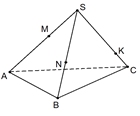
На рёбрах SA, SB, SC тетраэдра SABC отмечены точки соответственно M, N и K.

Построить сечение тетраэдра плоскостью MNK

Рис. 3. Решение

Решение

На рисунке 2 изображён исходный тетраэдр.

При построении сечений первым делом соединяем точки, лежащие на одних плоскостях (гранях). В данном случае точки M и N лежат в плоскости ABS, поэтому их соединяем. Аналогично N и K, M и K. Тогда плоскость MNK пересекает грани тетраэдра по отрезкам MN, NK и MK. В совокупности плоскость представляет собой треугольник MNK, который и является сечением данного тетраэдра.

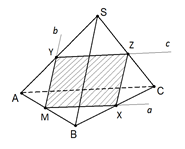
Пример 2

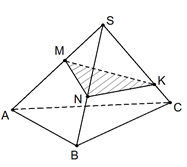
На рёбрах AB, SA, SC тетраэдра SABC отмечены точки соответственно M, N и K. Построить сечение тетраэдра плоскостью MNK.

Рис. 4. К примеру 2

Решение

Построим прямую, по которой плоскость MNK пересекает плоскость грани ABC. Точка M является общей точкой этих плоскостей. Чтобы построить ещё одну общую точку, продолжим отрезки KN и AC до их пересечения в точке E (рис. 4, б), которая и является второй общей точкой плоскостей MNK и ABC. Значит, эти плоскости пересекаются по прямой ME. Прямая ME пересекает ребро BC в некоторой точке Q. Четырёхугольник MNKQ – искомое сечение.

Если точки N и K расположены таким образом, что прямые NK и AC параллельны, то прямая NK параллельна грани ABC и, следовательно, плоскость MNK пересекает грань ABC по некоторой прямой MF, параллельной NK. Вторая общая точка плоскостей ABC и MNK (точка Q) находится на пересечении MF и BC (рис. 4, в).

Пример 3

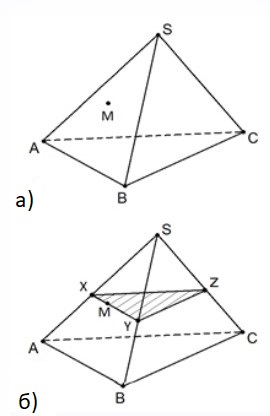
Точка M лежит на боковой грани ABS тетраэдра SABC (рис. 5, а).

Построить сечение тетраэдра плоскостью, проходящей через точку M параллельно основанию ABC.

Рис. 5. К примеру 3

Решение

Так как секущая плоскость параллельна плоскости ABC, то она параллельна прямым AB, BC и CA. Значит, секущая плоскость пересекает боковые грани тетраэдра по прямым, параллельным сторонам треугольника ABC. Проведём через точку M прямую, параллельную отрезку AB и обозначим буквами X и Y точки пересечения этой прямой с боковыми рёбрами SA и SB (рис. 5. б). Теперь через точку X проведём прямую, параллельную отрезку AC. Обозначим точку пересечения этой прямой с ребром SC буквой Z. Проведем отрезок YZ.

Треугольник XYZ является искомым сечением.

Упражнение 2

1. Может ли сечением тетраэдра быть:

а) треугольник;

б) четырёхугольник;

в) пятиугольник.

2. В тетраэдре SABC точки M, N, K – середины рёбер SA, SB, SC соответственно. Найдите площадь сечения тетраэдра SABC плоскостью MNK, если площадь треугольника ABC равна 80 см².

3. Изобразите тетраэдр SABC и отметьте точку M на ребре AB. Постройте сечение тетраэдра плоскостью, проходящей через точку M параллельно прямым AC и SB.

Контрольные вопросы

Какая геометрическая фигура называется тетраэдром?
Что представляет собой сечение тетраэдра?
Какие геометрические фигуры могут являться сечением тетраэдра?

Ответы

Упражнение 1

1.(рис. 6)

а) EMNK; грани – EMK, EKN, EMN, MNK; ребра – MK, KN, MN, EM, EK, EN; вершины – E, M, N, K.

б) MK и EN, MN и EK, KN и EM.

Рис. 6. К упражнению 1

Упражнение 2

1.а) да; б) да; в) нет

2. 20 см²

3. Через точку M проведём прямую a, параллельную AC;

обозначим точку пересечения прямых a и BC буквой X;

через точку M проведём прямую b, параллельную SB;

обозначим точку пересечения прямых b и SA буквой Y;

через точку Y проведём прямую c, параллельную AC;

обозначим точку пересечения прямых c и SC буквой Z;

Четырёхугольник MYZX – искомое сечение.

Рис. 7. К упражнению 2

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Найдите площадь сечения правильного тетраэдра PABC плоскостью, параллельной рёбрам PA и PC и проходящей через середину ребра PB, если все рёбра тетраэдра равны 8.

Найдите площадь сечения правильного тетраэдра PABC плоскостью, параллельной рёбрам PA и PC и проходящей через середину ребра PB, если все рёбра тетраэдра равны 4.

Аналоги к заданию № 488: 489 Все

Найдите площадь сечения правильного тетраэдра PABC плоскостью, проходящей через середины рёбер BC и PC параллельно ребру AC, если все рёбра тетраэдра равны 10.

Найдите площадь сечения правильного тетраэдра PABC плоскостью, проходящей через середины рёбер BC и PC параллельно ребру AC, если все рёбра тетраэдра равны 6.

Аналоги к заданию № 490: 491 Все

Найдите площадь сечения правильного тетраэдра PABC плоскостью, проходящей через точки, делящие рёбра PC и BC в отношении 2:1, считая от вершины C, параллельно ребру BP, если все рёбра тетраэдра равны 3.

Пройти тестирование по этим заданиям

Источник

2023-03-27

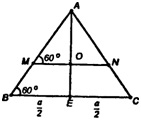
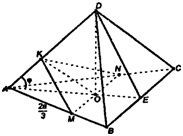
Дан правильный тетраэдр с ребром $a$. Найдите площадь сечения плоскостью, проходящей через центры трёх его граней.

Решение:

Пусть $M$, $K$ и $N$ — центры граней соответственно $ABC$, $BCD$ и $ABD$ правильного тетраэдра $ABCD$, а $P$ и $Q$ — середины рёбер соответственно $AB$ и $BC$.
Поскольку $DN:NP=DK:KQ=2:1$, прямая $NK$ параллельна $PQ$. Значит, прямая $NK$ параллельна плоскости $ABC$. Секущая плоскость проходит через прямую $NK$, параллельную плоскости $ABC$ и имеет с плоскостью $ABC$ общую точку $M$, следовательно, эти плоскости пересекаются по прямой $l$, параллельной $NK$, а значит, и $PQ$ (см. задачу @H8003). Пусть прямая $l$ пересекает рёбра $AB$ и $BC$ в точках $E$ и $F$ соответственно, а $T$ — середина $AC$. Тогда

$BE:AB=BF:BC=BM:BT=2:3.$

Аналогично получим, что секущая плоскость пересекает ребро $BD$ в точке $L$, для которой $BL:BD=2:3$. Значит, сечение тетраэдра плоскостью $MKN$ — треугольник $ELF$, подобный треугольнику $ADC$ с коэффициентом $frac{2}{3}$. Следовательно,

$S_{Delta ELF}=left(frac{2}{3}right)^{2}S_{Delta ADC}=frac{4}{9}cdotfrac{a^{2}sqrt{3}}{4}=frac{a^{2}sqrt{3}}{9}.$

Источник

я могу помочь с этим заданием

а) Пусть т. О — центр грани АВС. Построим МК || DB, MN || ВС.
пл .MKN — искомое сечение.
Пусть ребро тетраэдра равно а. Тогда

Т.к. ΔADB — равносторонний, а КМ || DB, то ΔАМК — также равносторонний, АМ=КМ=
(углы с соответственно параллельными и одинаково направленными сторонами):

б) Построим отрезок в пл. ADO. Т.к. пл.то
Т.к. и то
Значит, ΔKMN — искомое сечение,
ΔAMN — равносторонний, MN = AM =

Из ΔADE по теореме косинусов имеем:
DE² = AD² + АЕ² — 2 ∙ AD ∙ АЕ ∙ cos φ,

Источник

Тетраэдр. Виды тетраэдров

Тетраэдр (четырёхгранник) — многогранник, гранями которого являются четыре треугольника (от греческого tetra — четыре и hedra — грань).

Рис. 1

У тетраэдра (4) грани, (4) вершины и (6) рёбер (Рис. 1).

Один из треугольников называется основанием тетраэдра, а три остальные — боковыми гранями тетраэдра.

В зависимости от видов треугольников и их расположения выделяют разные виды тетраэдров.

В школьном курсе чаще говорят о следующих видах тетраэдра:

— равногранный тетраэдр, у которого все грани — равные между собой треугольники;

— правильная треугольная пирамида — основание — равносторонний треугольник, все боковые грани — одинаковые равнобедренные треугольники (Рис. 3);

— правильный тетраэдр, у которого все четыре грани — равносторонние треугольники (Рис. 2).

Рис. 2 Рис. 3

Свойство правильного тетраэдра:

из определения правильного многогранника следует, что все рёбра тетраэдра имеют равную длину, а грани — равную площадь.

Параллелепипед. Виды параллелепипедов

Параллелепипедом называется многогранник, у которого (6) граней — параллелограммы.

Рис. 4

У параллелепипеда, как отмечено, (6) граней, (8) вершин и (12) рёбер (Рис. 4).

Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих рёбер — противоположными.

Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани — боковыми гранями параллелепипеда.

Рёбра параллелепипеда, не принадлежащие основаниям, называют боковыми рёбрами.

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда (Рис. 5).

Рис. 5

В зависимости от видов параллелограммов и их расположения выделяют разные виды параллелепипедов:

параллелепипеды могут быть прямые и наклонные.

У прямых параллелепипедов боковые грани — прямоугольники (Рис. 5),

у наклонных — параллелограммы (Рис. 4).

Прямой параллелепипед, у которого основанием тоже является прямоугольник, называется прямоугольным параллелепипедом.

Рис. 6

Длины непараллельных рёбер прямоугольного параллелепипеда называются его линейными размерами (измерениями).

У прямоугольного параллелепипеда — три линейных размера:

DD1

(Рис. 6).

Свойства параллелепипеда:
— противоположные грани параллелепипеда равны и параллельны.

— Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

— Боковые грани прямого параллелепипеда — прямоугольники.

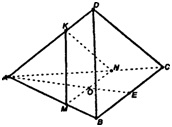
Построение сечения тетраэдра и параллелепипеда

Плоскостью сечения многогранника можно назвать любую плоскость, по обе стороны которой находятся точки многогранника.

Секущая плоскость пересекает грани многогранников по отрезкам.

Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

Так как у тетраэдра (4) грани, то сечением тетраэдра может быть треугольник (Рис. 7) или

четырёхугольник (Рис. 8).

Рис. 7 Рис. 8

У параллелепипеда (6) граней, поэтому сечением этого многогранника может быть треугольник (Рис. 9), четырёхугольник ( Рис. 10), пятиугольник (Рис. 11) или шестиугольник (Рис. 12).

При построении сечения надо вспомнить следующие знания из предыдущих тем:

1. если две точки прямой принадлежат плоскости, то прямая находится в этой плоскости.

2. Если две плоскости имеют общую точку, то эти плоскости пересекаются по прямой.

3. Если плоскость пересекает две параллельные плоскости, то линии пересечения параллельны.

Пример:

Задача

Построить сечение параллелепипеда плоскостью, которая проходит через точки (K), (M) и (N).

1. Проводим (MK), так как обе точки находятся в одной плоскости;

MK∩CC1=X

— непараллельные прямые в одной плоскости пересекаются;

3. проводим (XN), так как обе точки находятся в одной плоскости;

5. проводим (MP), так как обе точки находятся в одной плоскости;

6. через точку (N) в плоскости основания

NL∥MP

, так как линии пересечения параллельных плоскостей с третьей плоскостью должны быть параллельны;

7. соединяем (N) и (L) и получаем сечение (MPNLK).

Источник