Как найти площадь сегмента эллипса - Исправление недочетов и поиск решений вместе с Examum.ru

Площадь сегмента эллипса

Главная
/
Математика
/
Геометрия
/
Площадь сегмента эллипса

Чтобы посчитать площадь сегмента эллипса воспользуйтесь нашим онлайн калькулятором:

Онлайн калькулятор

Длинная

Короткая

Высота сегмента

h =

Результат:
Площадь сегмента эллипса

S_сэ =

Округление ответа:

Просто введите данные и получите ответ.

Теория

Чему равна площадь сегмента эллипса S_сэ, если известны высота сегмента h, длинная и короткая оси эллипса (D и d)?

Формула

S_сэ = D ⋅ d4⋅ (arccos (1 — 2hd) — (1 — 2hd) ⋅ √4hd — 4h²d²)

Пример

К примеру, для эллипса с длинной осью D = 6 см и короткой – d = 4 см, посчитаем площадь сегмента эллипса, имеющего высоту h = 1 см:

S_сэ = 6 ⋅ 44⋅ (arccos (1 — 2 ⋅ 14) — (1 — 2 ⋅ 14) ⋅ √4 ⋅ 14 — 4 ⋅ 1²4²) =

= 6 ⋅ (arccos 0.5 — 0.5 ⋅ √1 — 0.25) = 6 ⋅ (1,047 — 0.433) = 3.684 см²

См. также

Источник

Сегмент, перпендикулярный большой оси эллипса

Сегмент, перпендикулярный малой оси эллипса

Площадь сегмента эллипса — это число, характеризующее сегмент эллипса в единицах измерения площади.

Сегмент эллипса — это часть эллипса, отсекаемая прямой.

Рассмотрим (меньшие) сегменты эллипса, отсекаемые прямой перпендикулярной одной из осей эллипса.

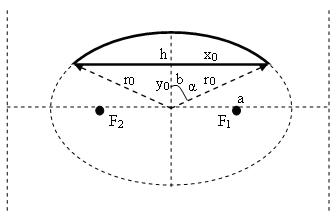
Обозначения[править]

Введём обозначения:

a — большая полуось эллипса;

b — малая полуось эллипса;

h — высота сегмента;

x₀ — абсцисса крайней точки сегмента;

y₀ — ордината крайней точки сегмента;

r₀ — расстояние (крайний радиус) от центра эллипса до крайней точки сегмента;

α — угол между осью симметрии сегмента и радиусом крайней точки сегмента;

S_{сегм.элл} — площадь сегмента эллипса.

Формулы[править]

Площадь сегмента, перпендикулярного большой оси эллипса[править]

Площадь сегмента, перпендикулярного малой оси эллипса[править]

Вывод формул[править]

Площадь сегмента, перпендикулярного большой оси эллипса[править]

1-й способ[править]

Для вывода используется формула «площадь плоской фигуры» в прямоугольных координатах.
Для нахождения интеграла используется формула 3 «интегралы функций с корнями».

2-й способ[править]

Для вывода используется формула «площадь плоской фигуры» в прямоугольных координатах.
Для нахождения интеграла используется «метод замены переменных» и переход к

полярным координатам.

Площадь сегмента, перпендикулярного малой оси эллипса[править]

1-й способ[править]

Для вывода используется формула «площадь плоской фигуры» в прямоугольных координатах.
Для нахождения интеграла используется формула 3 «интегралы функций с корнями».

2-й способ[править]

Для вывода используется формула «площадь плоской фигуры» в прямоугольных координатах.
Для нахождения интеграла используется «метод замены переменных» и переход к

полярным координатам.

Площадь сегмента[править]

Площадь меньшего сегмента равна разности площадей соответствующего сектора и треугольника (дополняющего сегмент до сектора).

Площадь большего сегмента равна сумме площадей соответствующего сектора и треугольника (дополняющего сектор до сегмента).

Сумма площадей меньшего и большего сегментов равна площади эллипса.

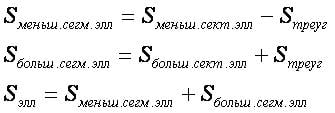
См. также[править]

Длина дуги эллипса

Другие формулы[править]

площадь плоской фигуры;
площадь круга;
площадь сегмента круга;
площадь сектора круга;
площадь серпа;
площадь эллипса;
площадь сегмента эллипса;
площадь сектора эллипса;
площадь серпа эллипса;
площадь сегмента параболы;
площадь сегмента гиперболы;
площадь сектора кардиоиды;
площадь сектора лемнискаты Бернулли;
площадь сегмента правильного многоугольника;
площадь сектора правильного многоугольника;
площадь арки синусоиды;
площадь арки косинусоиды;
площадь, ограниченная тангенсоидой и осью абсцисс;
площадь, ограниченная котангенсоидой и осью абсцисс;
площадь арки циклоиды;
площадь, ограниченная цепной линией и осью абсцисс;
площадь, ограниченная трактрисой и осью абсцисс.

Ссылки[править]

Участник:Logic-samara

Источник

Определение эллипсa

Определение.

Эллипс — это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек F₁ и F₂ равна постоянной величине. Точки F₁ и F₂ называют фокусами эллипса.

F₁M₁ + F₂M₁ = F₁M₂ + F₂M₂ = A₁A₂ = const

Элементы эллипсa

F₁ и F₂ — фокусы эллипсa

Оси эллипсa.

А₁А₂ = 2a — большая ось эллипса (проходит через фокусы эллипса)

B₁B₂ = 2b — малая ось эллипса (перпендикулярна большей оси эллипса и проходит через ее центр)

a — большая полуось эллипса

b — малая полуось эллипса

O — центр эллипса (точка пересечения большей и малой осей эллипса)

Вершины эллипсa A₁, A₂, B₁, B₂ — точки пересечения эллипсa с малой и большой осями эллипсa

Диаметр эллипсa — отрезок, соединяющий две точки эллипса и проходящий через его центр.

Фокальное расстояние c — половина длины отрезка, соединяющего фокусы эллипсa.

Эксцентриситет эллипсa e характеризует его растяженность и определяется отношением фокального расстояния c к большой полуоси a. Для эллипсa эксцентриситет всегда будет 0 < e < 1, для круга e = 0, для параболы e = 1, для гиперболы e > 1.

Фокальные радиусы эллипсa r₁, r₂ — расстояния от точки на эллипсе до фокусов.

Радиус эллипсa R — отрезок, соединяющий центр эллипсa О с точкой на эллипсе.

R =	ab	=	b
√a²sin²φ + b²cos²φ	√1 — e²cos²φ

где e — эксцентриситет эллипсa, φ — угол между радиусом и большой осью A₁A₂.

Фокальный параметр эллипсa p — отрезок который выходит из фокуса эллипсa и перпендикулярный большой полуоси:

Коэффициент сжатия эллипсa (эллиптичность) k — отношение длины малой полуоси к большой полуоси. Так как малая полуось эллипсa всегда меньше большей, то k < 1, для круга k = 1:

k = √1 — e²

где e — эксцентриситет.

Сжатие эллипсa (1 — k ) — величина, которая равная разности между единицей и эллиптичностью:

Директрисы эллипсa — две прямые перпендикулярные фокальной оси эллипса, и пересекающие ее на расстоянии

от центра эллипса. Расстояние от фокуса до директрисы равно

Основные свойства эллипсa

1. Угол между касательной к эллипсу и фокальным радиусом r₁ равен углу между касательной и фокальным радиусом r₂ (Рис. 2, точка М₃).

2. Уравнение касательной к эллипсу в точке М с координатами (x_M, y_M):

3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, соединяющий середины отрезков образовавшихся при пересечении прямых и эллипса, всегда будет проходить через центр эллипсa. (Это свойство дает возможность построением с помощью циркуля и линейки получить центр эллипса.)

4. Эволютой эллипсa есть астероида, что растянута вдоль короткой оси.

5. Если вписать эллипс с фокусами F₁ и F₂ у треугольник ∆ ABC, то будет выполнятся следующее соотношение:

1 =	F₁A ∙ F₂A	+	F₁B ∙ F₂B	+	F₁C ∙ F₂C
CA ∙ AB	AB ∙ BC	BC ∙ CA

Уравнение эллипсa

Каноническое уравнение эллипсa:

Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa О в начале системы координат, а большая ось лежит на абсциссе, то эллипсa описывается уравнением:

Если центр эллипсa О смещен в точку с координатами (x_o, y_o), то уравнение:

1 =	(x — x_o)²	+	(y — y_o)²
a²	b²

Параметрическое уравнение эллипсa:

{	x = a cos α	де 0 ≤ α < 2π
y = b sin α

Радиус круга вписанного в эллипс

Круг, вписан в эллипс касается только двух вершин эллипсa B₁ и B₂. Соответственно, радиус вписанного круга r будет равен длине малой полуоси эллипсa OB₁:

r = b

Радиус круга описанного вокруг эллипсa

Круг, описан вокруг эллипсa касается только двух вершин эллипсa A₁ и A₂. Соответственно, радиус описанного круга R будет равен длине большой полуоси эллипсa OA₁:

R = a

Площадь эллипсa

Формула определение площади эллипсa:

S = πab

Площадь сегмента эллипсa

Формула площади сегмента, что находится по левую сторону от хорды с координатами (x, y) и (x, -y):

S =	πab	—	b	(	x	√	a² — x² + a² ∙ arcsin	x	)
2	a	a

Периметр эллипсa

Найти точную формулу периметра эллипсa L очень тяжело. Ниже приведена формула приблизительной длины периметра. Максимальная погрешность этой формулы ~0,63 %:

L ≈ 4	πab + (a — b)²
a + b

Длина дуги эллипсa

Формулы определения длины дуги эллипсa:

1. Параметрическая формула определения длины дуги эллипсa через большую a и малую b полуоси:

	t₂
l =	∫	√a²sin²t + b²cos²t dt
	t₁

2. Параметрическая формула определения длины дуги эллипсa через большую полуось a и эксцентриситет e:

	t₂
l =	∫	√1 — e²cos²t dt, e < 1
	t₁

Источник

Как найти площадь сегмента эллипса?

[править] Площадь сегмента Площадь большего сегмента равна сумме площадей соответствующего сектора и треугольника (дополняющего сектор до сегмента). Сумма площадей меньшего и большего сегментов равна площади эллипса.

Что такое площадь кругового сегмента?

Круговой сегмент (сегмент) — это часть круга, ограниченная дугой окружности и хордой, которая соединяет концы этой дуги: В том случае когда градусная мера дуги меньше 1800, площадь сегмента равна разности площади сектора и площади равнобедренного треугольника, сторонами которого являются два радиуса и хорда сегмента.

Как найти площадь половины круга?

Советы

Площадь круга вычисляется по формуле: (пи)(r^2).
Площадь полукруга вычисляется по формуле: (1/2)(пи)(r^2).

Как найти сегмент круга?

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой)….Формулы расчетов

Формула	Численное решение
αg=180απ	нет
h=R(1−cosα2)	нет
c=2Rsinα2	нет
S=R22(α−sinα)	нет

Как вычислить площадь цилиндра формула?

Для нахождения полной площади цилиндра нужно к полученной Sбок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле Sо = 2π * r2. Конечная формула выглядит следующим образом: Sпол = 2π * r2 + 2π * r * h.

Что такое площадь сегмента?

Площадь сегмента можно найти как разность площадей сектора круга и этого равнобедренного треугольника.

Что такое круговой сектор?

Сектор круга — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Как посчитать часть круга?

Площадь сектора круга – это часть S всей плоской фигуры, ограниченной окружностью с радиусом r. Площадь круга равна произведению квадрата радиуса на число «пи». Площадь сектора может быть выражена формулой S = π х r² х α/360.

Как обозначается сегмент круга?

Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами. Определение.

Как называется сегмент круга?

Сегме́нт кру́га, кругово́й сегмент — часть круга, ограниченная дугой окружности и её хордой или секущей.

Как найти площадь емкости?

V=Sкр х L — расчет объема цилиндра, где Sкр — площадь поперечного сечения цилиндра, L — длина цилиндрической части. Площадь поперечного сечения емкости в форме цилиндра рассчитывается по формуле: Sкр=3,14·d2/4 — площадь круга с диаметром d.

Как найти площадь дна цилиндра?

Основаниями цилиндра (их два: верхние и нижнее) являются окружности, их легко определить. Известно, что площадь окружности равна πr2. Поэтому, формула площади двух окружностей (двух оснований цилиндра) будет иметь вид πr2 + πr2 = 2πr2.

Что называется сегментом?

Сегмент (от лат. segmentum — отрезок, полоса, от seco — режу, рассекаю) — часть чего-либо. Сегмент памяти — одна из единиц адресации в некоторых моделях памяти (сегментная адресация памяти).

Как вычислить площадь части окружности?

Площадь сектора круга – это часть S всей плоской фигуры, ограниченной окружностью с радиусом r. Площадь круга равна произведению квадрата радиуса на число «пи». Площадь сектора может быть выражена формулой S = π х r² х α/360. В ином виде при указании угла сектора α не в градусах, а в радианах, S = (α/2) х r².

Как найти длину сектора круга?

Площадь кругового сектора

Длина дуги окружности радиуса равна C α = 2 π R ⋅ α 360 , где – градусная мера этой дуги.
Площадь кругового сектора круга радиуса равна S α = π R 2 ⋅ α 360 , где – градусная мера дуги сектора.
Тогда длина дуги в равна C α = 2 π R ⋅ α 360 .

Как найти сегмента?

Площадь сегмента можно найти как разность площадей сектора круга и этого равнобедренного треугольника.

Как находить сегмент?

Для того чтобы вычислить площадь сегмента круга, нужно вычесть из площади сектора круга площадь отсеченного треугольника.

Источник

A calculus-free derivation:

Consider the analagous figure drawn for a unit circle. We find the area (assuming an angle is given as $theta$) as
$$
A = frac12(theta-sintheta)
$$

Stretch the graph left-right by a factor of $a$, and stretch it up-down by a factor of $b$. Having stretched the region with the rest of the picture, we can deduce that the new area will be
$$
A = frac{ab}{2}(theta-sintheta)
$$
Where $theta$ is still the angle of our squished ellipse. To make this a complete formula, we must find an expression for $theta$ given an elliptical angle.

In fact, if we are given an elliptical angle $phi$ from the x-axis, we have
$$
theta = arctanleft[frac{a}b tanphiright] =
$$
Which gives us
$$
A = frac{ab}{2}left(arctanleft[frac{a}b tanphiright]-sinleft(arctanleft[frac{a}b tanphiright]right)right)
$$
In the case that $phi$ is not given as an angle from the x-axis, we can break $phi$ into $phi = phi_1+phi_2$, where $phi_1$ is the part of the angle going clockwise from the x-axis, and $phi_2$ is the counterclockwise part from the x-axis. We then have

$$
theta = arctanleft[frac{a}bphi_1right] + arctanleft[frac{a}bphi_2right]\
%tantheta= abfrac{tanphi_1+tanphi_2}{1-a^2tanphi_1tanphi_2}
$$
Which can be substituted as before.

This was more complicated than I expected it to be.

Please comment, edit, or let me know if there is anything I have left out that makes this answer less understandable.

Источник