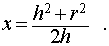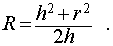Как найти площадь шара описанного около конуса

В данной публикации мы рассмотрим, как найти радиус описанной около конуса сферы, а также площадь ее поверхности и объем шара, ограниченного этой сферой.

Нахождение радиуса сферы/шара

Около любого конуса можно описать сферу (шар). Другими словами, в любую сферу можно вписать конус.

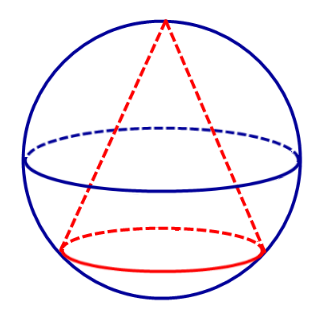
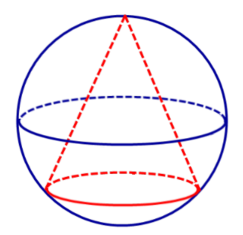
Чтобы найти радиус сферы (шара), описанной около конуса, чертим осевое сечение конуса. В итоге у нас получится равнобедренный треугольник (в нашем случае – ABC), вокруг которого описана окружность с радиусом r.

Радиус основания конуса (R) равен половине основания треугольника (AC), а образующие (l) – его боковые стороны (AB и BC).

Радиус окружности (r), описанной вокруг треугольника ABC, в том числе, является радиусом шара, описанного около конуса. Он находится по следующим формулам:

1. Через образующую и радиус основания конуса:

2. Через высоту и радиус основания конуса

Высота (h) конуса – это отрезок BE на рисунках выше.

Формулы площади и объема сферы/шара

Зная радиус (r) можно найти площадь поверхности (S) сферы и объем (V) шара, ограниченного этой сферой:

Примечание: π округленно равняется 3,14.

куба равен 3.Найдите площадь поверхности куба… 3)В шар площадь поверхности которого равна 100n, вписан цилиндр.Найдите высоту цилиндра, если радиус его основания равен 4… 4)В шар вписан конус… Найдите высоту конуса, еслирадиус шара равен 5, а радиус основания конуса равен 4

Сфера, описанная около конуса.
Отношение объемов конуса и описанной около него сферы

Определение 1. Конусом, вписанным в сферу, называют такой конус, у которого вершина и окружность основания лежат на сфере (рис. 1).

Определение 2. Если конус вписан в сферу, то сферу называют описанной около конуса.

Утверждение. Около любого конуса можно описать сферу, причем только одну. Центр описанной сферы лежит на оси конуса.

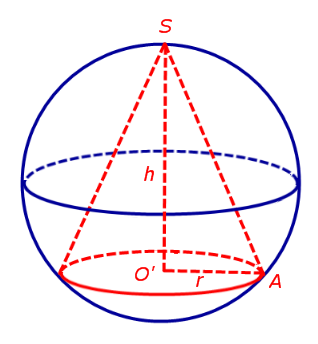
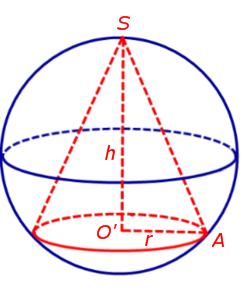
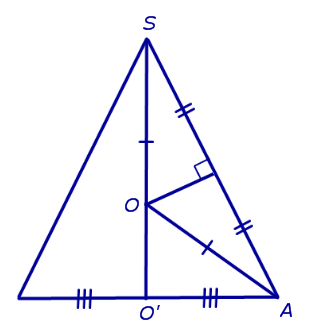
Доказательство. Рассмотрим конус высоты h, в основании которого лежит круг радиуса r с центром в точке O’ . Обозначим буквой S вершину конуса, а буквой A – произвольную точку на окружности основания конуса (рис. 2).

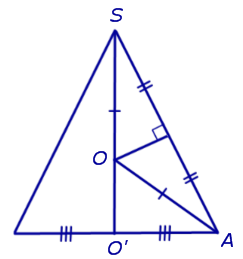
Рассмотрим сечение конуса плоскостью ASO’ и проведем серединный перпендикуляр к отрезку SA . Обозначим буквой O точку пересечения этого серединного перпендикуляра с прямой SO’ и соединим точку O с точкой A (рис. 3).

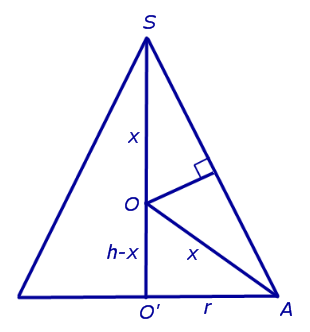
По свойству серединного перпендикуляра точка O находится на одинаковом расстоянии от точек A и S . Обозначим это расстояние через x и покажем, что x не зависит от выбора точки A (рис. 4).

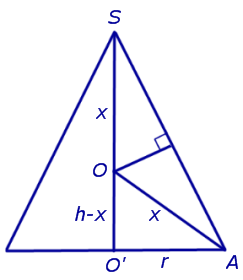
Действительно, с помощью теоремы Пифагора из прямоугольного треугольника AOO’ получим:

Таким образом, мы установили, что точка O находится на одном и том же расстоянии x, которое зависит лишь от высоты и радиуса основания конуса, от всех точек окружности основания конуса и от его вершины S . Значит, точка O – центр сферы, описанной около конуса.

Для доказательства единственности описанной около конуса сферы заметим, что точка, равноудаленная от всех точек окружности основания конуса, должна лежать на перпендикуляре к плоскости основания конуса, проходящем через центр этой окружности. А точка, равноудаленная от вершины конуса и от какой-либо точки на окружности основания конуса, должна лежать на серединном перпендикуляре к образующей конуса, проходящей через эту точку. Таким образом, центром сферы, описанной около конуса, может быть лишь построенная выше точка O .

Следствие 1. Радиус сферы, описанной около конуса с радиусом основания r и высотой h равен

Следствие 2. Отношение объема конуса к объему описанной около него сферы можно найти по формуле

Нахождение радиуса/площади/объема описанной около конуса сферы (шара)

В данной публикации мы рассмотрим, как найти радиус описанной около конуса сферы, а также площадь ее поверхности и объем шара, ограниченного этой сферой.

Нахождение радиуса сферы/шара

Около любого конуса можно описать сферу (шар). Другими словами, в любую сферу можно вписать конус.

Чтобы найти радиус сферы (шара), описанной около конуса, чертим осевое сечение конуса. В итоге у нас получится равнобедренный треугольник (в нашем случае – ABC), вокруг которого описана окружность с радиусом r.

Радиус основания конуса (R) равен половине основания треугольника (AC), а образующие ( l ) – его боковые стороны (AB и BC).

Радиус окружности (r), описанной вокруг треугольника ABC, в том числе, является радиусом шара, описанного около конуса. Он находится по следующим формулам:

1. Через образующую и радиус основания конуса:

2. Через высоту и радиус основания конуса

Высота (h) конуса – это отрезок BE на рисунках выше.

Формулы площади и объема сферы/шара

Зная радиус (r) можно найти площадь поверхности (S) сферы и объем (V) шара, ограниченного этой сферой:

Примечание: π округленно равняется 3,14.

Вписанные и описанные конусы.

Презентация для учащихся 11 класса по теме «Комбинация тел» содержит краткую теорию и примеры решения задач на комбинации конуса и шара, конуса и пирамиды. Будет полезна при подготовке к ЕГЭ.

Просмотр содержимого документа
«Вписанные и описанные конусы.»

Пирамида, вписанная в конус

Пирамида называется вписанной в конус, если ее основание вписано в основание конуса, а вершина совпадает с вершиной конуса. При этом конус называется описанным около пирамиды.

Около пирамиды можно описать конус тогда и только тогда, когда около ее основания можно описать окружность.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Найдите сторону основания правильной треугольной пирамиды, вписанной в конус, радиус основания которого равен 1.

Найдите сторону основания правильной четырехугольной пирамиды, вписанной в конус, радиус основания которого равен 1.

Найдите сторону основания правильной шестиугольной пирамиды, вписанной в конус, радиус основания которого равен 1.

Пирамида, описанная около конуса

Пирамида называется описанной около конуса, если ее основание описано около основания конуса, а вершина совпадает с вершиной конуса. При этом конус называется вписанным в пирамиду.

В пирамиду можно вписать конус тогда и только тогда, когда в ее основание можно вписать окружность.

Найдите сторону основания правильной треугольной пирамиды, описанной около конуса, радиус основания которого равен 1.

Найдите сторону основания правильной четырехугольной пирамиды, описанной около конуса, радиус основания которого равен 1.

Найдите сторону основания правильной шестиугольной пирамиды, описанной около конуса, радиус основания которого равен 1.

Сфера, вписанная в конус

Сфера называется вписанной в конус, если она касается его основания и боковой поверхности (касается каждой образующей). При этом конус называется описанным около сферы.

В любой конус (прямой, круговой) можно вписать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, вписанной в треугольник, являющийся осевым сечением конуса.

Напомним, что радиус r окружности, вписанный в треугольник, находится по формуле

где S – площадь, p – полупериметр треугольника.

В конус, радиус основания которого равен 1, а образующая равна 2, вписана сфера. Найдите ее радиус.

Решение. Треугольник SAB равносторонний. Высота SH равна Площадь S равна Полупериметр p равен 3. По формуле r = S/p получаем

В конус, радиус основания которого равен 2, вписана сфера радиуса 1. Найдите высоту конуса.

Решение. Обозначим h высоту SH конуса . Из формулы r = S/p имеем:

Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45 о . Найдите радиус вписанной сферы.

Решение. Высота SH конуса равна 1. Образующая .

Полупериметр p равен

По формуле r = S/p , имеем

Высота конуса равна 8, образующая 10. Найдите радиус вписанной сферы.

Решение. Радиус основания конуса равен 6. Площадь треугольника SFG равна 48, полупериметр 16. По формуле r = S/p имеем r = 3.

Можно ли вписать сферу в наклонный конус?

Сфера, вписанная в усеченный конус

Сфера называется вписанной в усеченный конус, если она касается его основани й и боковой поверхности (касается каждой образующей). При этом усеченный конус называется описанным около сферы.

В усеченный конус можно вписать сферу, если в его осевое сечение можно вписать окружность. Радиус этой окружности будет равен радиусу вписанной сферы.

В усеченный конус, радиусы оснований которого равны 2 и 1, вписана сфера. Найдите радиус сферы и высоту усеченного конуса.

Решение. Имеем: A 1 B = A 1 O 1 = 2, A 2 B = A 2 O 2 = 1. Следовательно, A 1 A 2 = 3 , A 1 C = 1.

В усеченный конус, радиус одного основания которого равен 2, вписана сфера радиуса 1. Найдите радиус второго основания.

Решение. Пусть A 1 O 1 = 2. Обозначим r = A 2 O 2 . Имеем: A 1 A 2 = 2+ r , A 1 C = 2 – r . По теореме Пифагора, имеет место равенство из которого следует, что выполняется равенство Решая полученное уравнение относительно r , находим

В усеченном конусе радиус большего основания равен 2, образующая наклонена к плоскости основания под углом 60 о . Найдите радиус вписанной сферы.

Решение. Заметим, что осевым сечением конуса, из которого получен усеченный конус, является равносторонний треугольник со стороной 2. Радиус r сферы, вписанной в усеченный конус, равен радиусу окружности, вписанной в этот равносторонний треугольник, т.е.

Образующая усеченного конуса равна 2, площадь осевого сечения 3. Найдите радиус вписанной сферы.

Решение. Воспользуемся формулой r = S/p , где S – площадь осевого сечения, p – полупериметр. В нашем случае S = 3 . Для нахождения полупериметра напомним, что для четырехугольника, описанного около окружности, суммы противоположных сторон равны. Значит, полупериметр равен удвоенной образующей цилиндра, т.е. p = 4. Следовательно, r = ¾.

Можно ли вписать сферу в усеченный наклонный конус.

Сфера, описанная около конуса

Сфера называется описанной около конуса, если вершина и окружность основания конуса лежат на сфере. При этом конус называется вписанным в сферу .

Около любого конуса (прямого, кругового) можно описать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, описанной около треугольника, являющимся осевым сечением конуса.

Напомним, что радиус R окружности, описанной около треугольника, находится по формуле

где S – площадь, a , b , c – стороны треугольника.

Около конуса, радиус основания которого равен 1, а образующая равна 2, описана сфера. Найдите ее радиус.

Решение. Треугольник SAB равносторонний со стороной 2. Высота SH равна Площадь S равна По формуле R = abc /4 S получаем

Около конуса, радиус основания которого равен 4, описана сфера радиуса 5. Найдите высоту h конуса.

Решение. Имеем, OB = 5 , HB = 4. Следовательно, OH = 3. Учитывая, что SO = OB = 5, получаем h = 8.

Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45 о . Найдите радиус описанной сферы.

Решение. Треугольник SAB – прямоугольный, равнобедренный. Следовательно, радиус R описанной сферы равен радиусу основания цилиндра, т.е. R = 1.

Высота конуса равна 8, образующая 10. Найдите радиус описанной сферы.

Решение. В треугольнике SAB имеем: SA = SB = 10, SH = 8. По теореме Пифагора, AH = 6 и, следовательно, S = 48. Используя формулу R = abc /4 S , получаем

Можно ли описать сферу около наклонного конуса?

Сфера, описанная около усеченного конуса

С фера называется описанной около усеченного конуса, если окружност и основани й усеченного конуса лежат на сфере. При этом усеченный к онус называется в писанным в сферу.

Около усеченного конуса можно описать сферу, если около его осевого сечения можно описать окружность. Радиус этой окружности будет равен радиусу описанной сферы.

Около усеченного конуса, радиусы оснований которого равны 2 и 1, а образующая равна 2, описана сфера. Найдите ее радиус.

Решение. Заметим, что A 1 O 1 B 2 O 2 и O 1 B 1 B 2 A 2 – ромбы. Треугольники A 1 O 1 A 2 , O 1 A 2 B 2 , O 1 B 1 B 2 – равносторонние и, значит, A 1 B 1 –диаметр. Следовательно, R = 2.

Радиус меньшего основания усеченного конуса равен 1, образующая равна 2 и составляет угол 45 о с плоскостью другого основания. Найдите радиус описанной сферы.

Решение. Имеем A 2 O 2 = 1, A 1 A 2 = 2, O 1 O 2 = , OO 1 = O 1 C = 1. Следовательно, OO 2 = 1 + и, значит,

Радиус одного основания усеченного конуса равен 4, высота 7, радиус описанной сферы 5. Найдите радиус второго основания усеченного конуса.

Решение. Имеем OO 1 = 3 , OO 2 = 4 и, следовательно, O 2 A 2 = 3.

Найдите радиус сферы, описанной около усеченного конуса, радиусы оснований которого равны 2 и 4, а высота равна 5.

Решение. Обозначим R радиус описанной сферы. Тогда

Учитывая, что O 1 O 2 = 6, имеем равенство

Решая его относительно R , находим

Можно ли описать сферу около усеченного наклонного конуса.

ответы

ваш ответ

похожие темы

похожие вопросы 5

ТЕЛА ВРАЩЕНИЯ

РЕШЕНИЕ ЗАДАЧ

Основные формулы

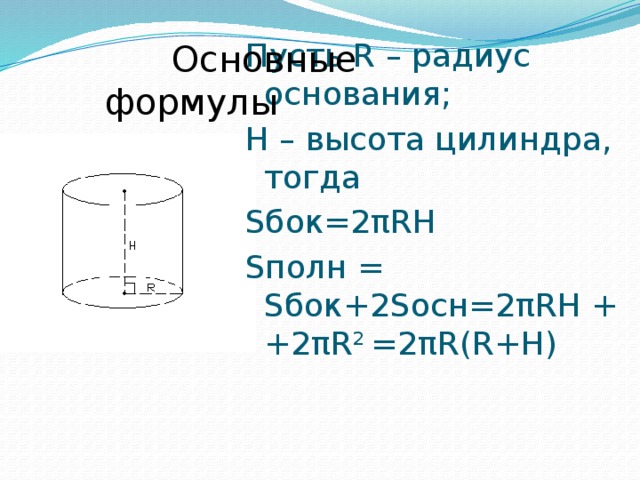
Пусть R – радиус основания;

H – высота цилиндра, тогда

Sбок=2πRH

Sполн = Sбок+2Sосн=2πRH + +2πR 2 =2πR(R+H)

Основные формулы

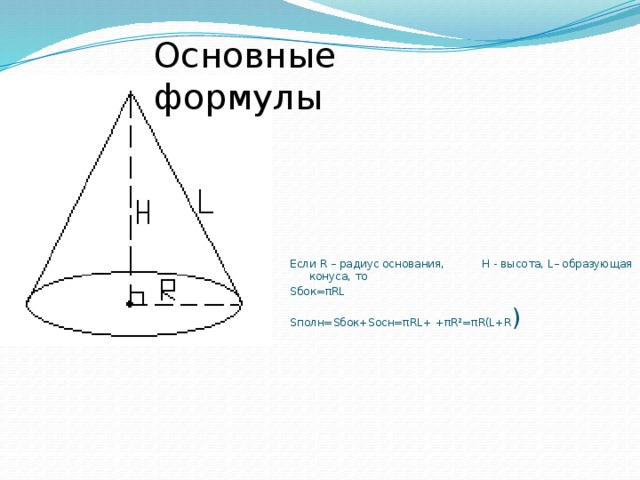
Если R – радиус основания, H — высота, L– образующая конуса, то

Sбок=πRL

Sполн=Sбок+Sосн=πRL+ +πR²=πR(L+R )

Усеченный прямой конус

h – высота усеченного конуса ; R и R1 – радиусы его верхнего и нижнего оснований; l – его образующая

Формулы:

Основные формулы

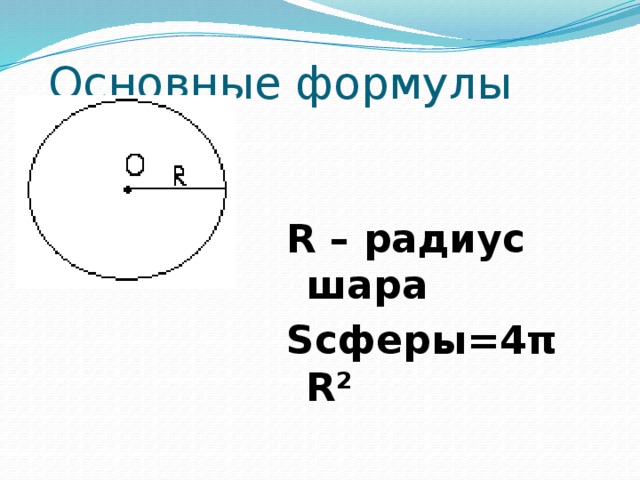
R – радиус шара

Sсферы=4πR²

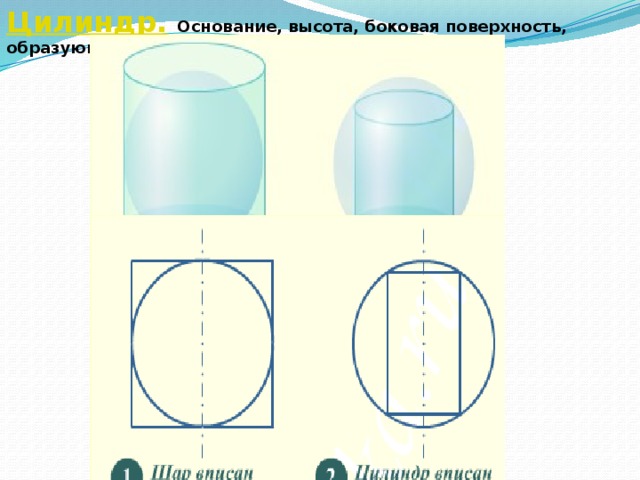
Цилиндр.   Основание, высота, боковая поверхность, образующая, развертка

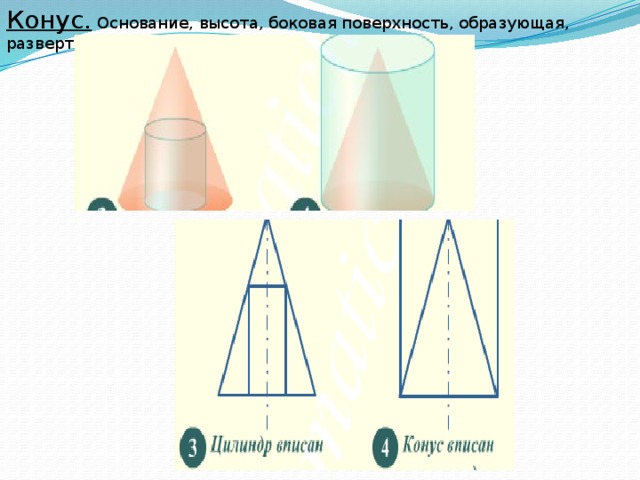
Конус.   Основание, высота, боковая поверхность, образующая, развертка

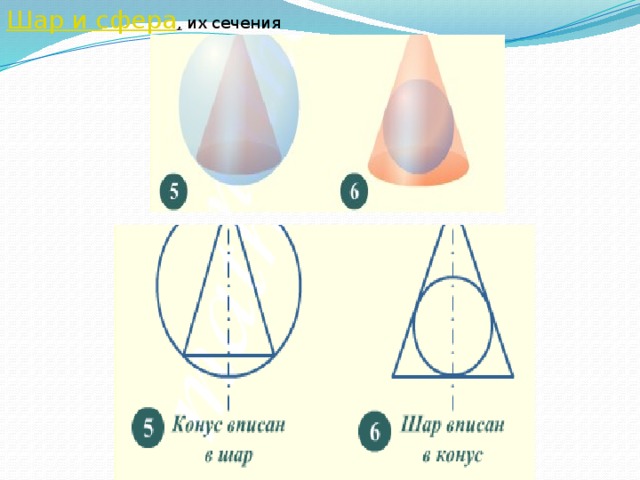
Шар и сфера ,   их сечения

Задача 1.

Шар вписан в цилиндр. Площадь поверхности шара равна 111.

Найдите площадь полной поверхности цилиндра.

Решение.

Площадь полной поверхности цилиндра находим по формуле  S ц  = 2 πrh  + 2 πr 2 .

Из рисунка (1) для плоского

сечения видно, что радиус

основания цилиндра ( r ) равен

радиусу вписанного шара ( R ),

а его высота ( h ) равна диаметру

шара (удвоенному радиусу).

Поэтому  S ц  = 2 πR ·2 R  + 2 πR 2  = 6 πR 2 . Величину  πR 2  найдем из формулы поверхности шара  S ш  = 4 πR 2 . Следовательно,  πR 2  =  S ш  / 4 = 111/4. Окончательно находим  S ц  = 6·111 / 4 = 333/2 = 166,5.

Ответ:  166,5

Задача 2

В шар, площадь поверхности которого равна 100π, вписан цилиндр. Найти высоту цилиндра, если радиус его основания равен 4.

Дополним чертеж осевого сечения радиусом шара и расставим буквы для обозначения отрезков.  Площадь поверхности шара  S ш  = 4 πR 2  = 100π. Отсюда  R 2  = 25 и  R  = 5. В треугольнике  OAB :  OA  =  x  — половина искомой высоты цилиндра;  AB  = 4 — радиус основания цилиндра;  OB  = 5 — радиус шара.  По теореме Пифагора: x 2  + 4 2  = 5 2  ,

x 2  = 25 − 16 = 9;  x  = 3.  h  = 6.

Ответ:  6

Задача 3

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 3√2. Найдите площадь боковой поверхности конуса.

  l  2  =  h  2  +  r  2 По условию задачи  h  =  r , следовательно  l  2  =  r  2  +  r  2 ;    l  2  = 2 r  2 ;     l  = √2· r . Площадь боковой поверхности цилиндра  S ц  = 2 πrh  = 2 πr  2 . Площадь боковой поверхности конуса  S к  =  πrl  =  πr ·√2· r  = √2 πr  2 ; т.е. площадь боковой поверхности цилиндра в √2 раз больше площади боковой поверхности конуса. Окончательно  S к  = 3√2 / √2 = 3/ Ответ:  3 A C B » width=»640″

Воспользуемся чертежом осевого сечения, расставим буквы для обозначения отрезков:  AC  =  h  — высота конуса и цилиндра,  CB  =  r  — радиус оснований конуса и цилиндра,  AB  =  l  — образующая цилиндра.

Из треугольника  ABC  по теореме Пифагора: AB 2  =  AC 2  +  CB 2  ==  l  2  =  h  2  +  r  2 По условию задачи  h  =  r , следовательно  l  2  =  r  2  +  r  2 ;    l  2  = 2 r  2 ;     l  = √2· r . Площадь боковой поверхности цилиндра 

S ц  = 2 πrh  = 2 πr  2 . Площадь боковой поверхности конуса  S к  =  πrl  =  πr ·√2· r  = √2 πr  2 ;

т.е. площадь боковой поверхности цилиндра в √2 раз больше площади боковой поверхности конуса. Окончательно  S к  = 3√2 / √2 = 3/ Ответ:  3

A

C

B

Задача 4

Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 7√2. Найдите радиус сферы.

Так как по условию задачи центр сферы находится в центре основания конуса, то основание конуса, в свою очередь, является диаметральным сечением сферы. Т.о. на плоском чертеже отрезок  AB  является диаметром окружности, и ∠ ACB  = 90° как вписанный угол, опирающийся на её диаметр.

Пусть  l  = 7√2 — образующая конуса,  R  — радиус сферы. Тогда в прямоугольном треугольнике  ABC   AC  =  BC  =  l  — катеты,  AB  = 2 R  — гипотенуза. По теореме Пифагора AB 2  =  AC 2  +  BC 2 ; (2 R ) 2  =  l  2  +  l  2 ; 4 R  2  =  l  2  +  l  2  = 2 l  2 ;   4 R  2  = 2(7√2_) 2 ; 4 R  2  = 2·49·2 = 4·49;    R  2  = 49;   R  = 7.

Ответ:  7

Задача 5

Найти площадь поверхности шара, описанного около конуса, у которого радиус основания   2/√π, а высота   1/√π.

Пусть  R  — радиус сферы. Поскольку  СD  — диаметр окружности осевого сечения, то  СH  +  HD  = 2 R . Воспользуемся свойством пересекающихся хорд окружности, чтобы найти длину отрезка  HD  =  x .

DH·HС = AH·HC; x ·  1/√π =   2/√π ·  2/√π; Преобразуя, получим  х  =   4/√π.  2 R  =   1/√π +   4/√π =  5/√π;    R  =  5/2√π. Площадь сферы  S  = 4π R 2  = 4π·25/4π = 25.

Ответ:  25

Задача 5

В шар вписан конус, образующая которого равна диаметру основания. Найти отношение полной поверхности этого конуса к поверхности шара.

Пусть образующая конуса ( AC  =  BC ) равна  a . Тогда по условию задачи диаметр конуса ( AB ) тоже равен  a . То есть, треугольник  ABC  — равносторонний.

Чтобы найти радиус шара ( R ), используем формулу, связывающую длину стороны равностороннего треугольника и радиус описанной около него окружности.

Радиус основания конуса  r  =  a /2 (половина диаметра).

Площадь полной поверхности конуса S к  = π r ( r  +  l ) = π· a /2·( a /2 +  a ) = 3π a 2 /4.

Площадь поверхности шара S ш  = 4π R 2  = 4π· a 2 ·(√3/3) 2  = 4π a 2 /3.

Их отношение

S к / S ш  = 3π a 2 /4/4π a 2 /3 =  9/16 = 0,5625.

Ответ:  0,5625

ЗАДАНИЕ НА ДОМ

№ 616

Задачи ЕГЭ (распечатка)