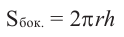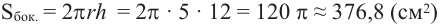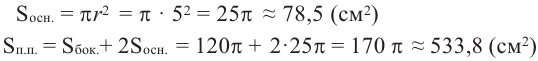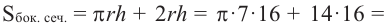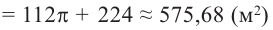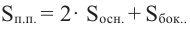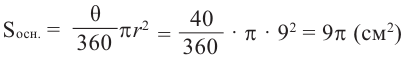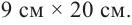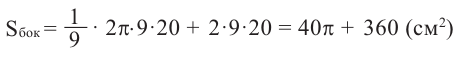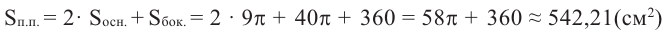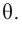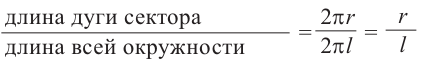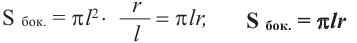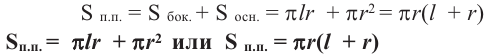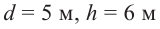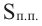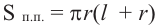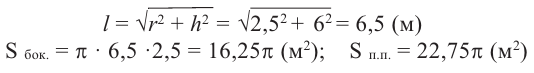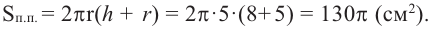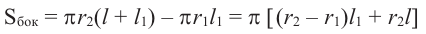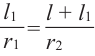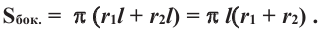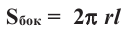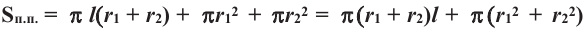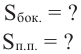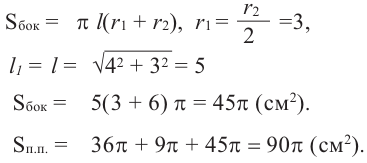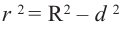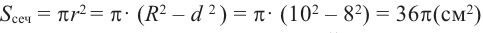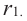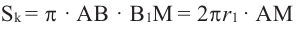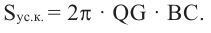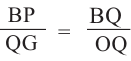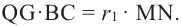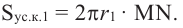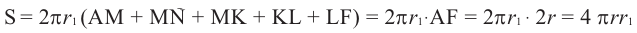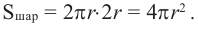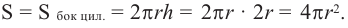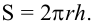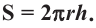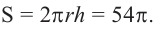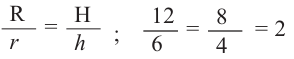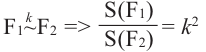Формулы объема
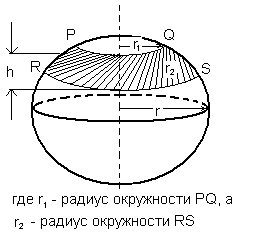
Объем и площадь шарового слоя и шарового пояса.
Объем шара равен 4/3π3 , а площадь сферы равна 4πr2.
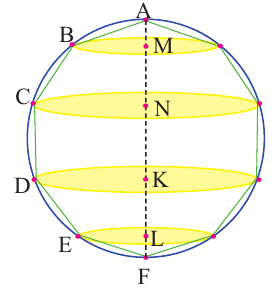
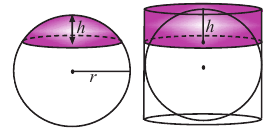
Шаровой слой — это часть шара между двумя параллельными плоскостями. На рисунке выше PQRS — шаровой слой.
Шаровой пояс — это сферическая поверхность шарового слоя.
Площадь шарового пояса на рисунке выше S=2 πhr;
Объем шарового слоя V=(πh/6)*(h2+3r12+3r22)
Пример1. Определение объема шарового слоя шара.
Определить объем шарового слоя шара с диаметром 50 см, если верхний и нижний диаметры слоя есть 25 и 40 см, а его высота 7,2 см.
Решение:
Как было сказано выше, объем шарового слоя
V=(πh/6)*(h2+3r12+3r22),
где h=7,2 см, r1= 25/2=12,5 см, r2=40/2=20 см
Следовательно, объем шарового слоя равен
V=(7,2π/6)*(7,22+3*12,52+3*202)=6483,18 см2 .
Пример 2. Определение площади шарового пояса.
Определить площадь шарового пояса из предыдущего примера.
Решение:
Площадь шарового пояса S=2πrh (как было определено выше), где радиус сферы r=50/2=25 см, а h=7,2 см.
Следовательно, площадь шарового пояса равна
S=2π*25*7,2=1130,4 см2
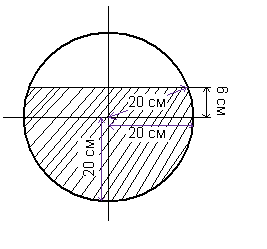
Пример 3. Определение объема заполнения сферического резервуара по уровню.
Сферический резервуар наполнен жидкостью до высоты 30 см. Определить объем жидкости в резервуаре (1л=1000 см3), если его внутренний диаметр равен 40 см.
Жидкость представлена в виде заштрихованной области в показанном на рис. ниже сечении.
Объем жидкости включает полусферу и шаровой пояс высотой 6 см.
Следовательно, объем жидкости есть V=(2/3)*πr3+(πh/6)*(h2+ 3r12+3r22), где
r2=40/2=20 см и r1=(202-62)1/2=19,1 см
Объем жидкости V=2/3 π *203+(6π)/6*(62+3*19,12+3*202)=24064,22 см3
Поскольку 1 литр =1000 см3, то количество литров жидкости равно
24064,22/1000=24,06422 л.
Содержание:
Великий греческий ученый Архимед был очень взволнован, когда он обнаружил, что отношение площади поверхности шара и описанного около него цилиндра и отношение их объемов равно 2:3. Великий математик, физик, инженер, Архимед, среди всех своих работ самой значимой считал именно эту. Он завещал на своей могильной плите выгравировать доказательство данной теоремы. Из истории известно, что долгое время его родной город Сиракузы, располагающийся на Сицилии, противостоял римлянам именно благодаря оружию, которое изобрел Архимед. Поэтому при взятии города римский военачальники приказал сохранить ученому жизнь. Но римский воин, который не знал Архимеда в лицо, убил его. Великий философ и писатель Цицерон потратил много времени, чтобы отыскать могилу Архимеда (по историческим сведениям он нашел ее через 137 лет). Это дело Цицерона стало идеей для работ многих художников.
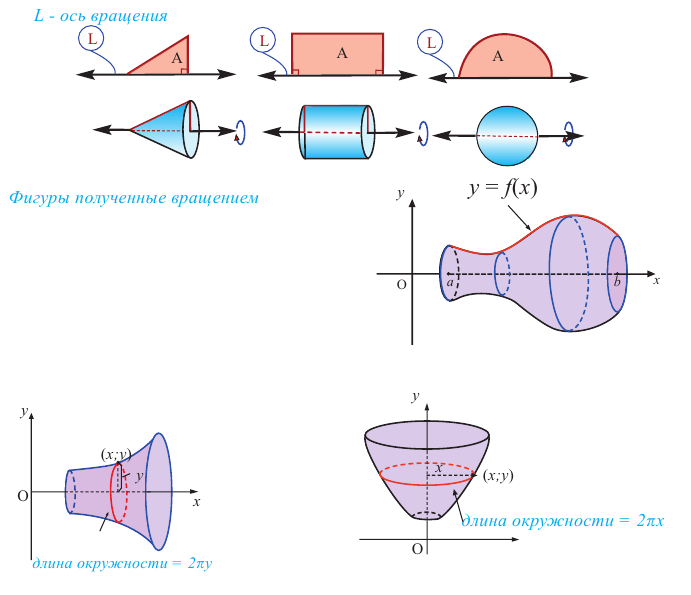
Определение фигур вращения
Гончарное ремесло позволяет создавать керамическую посуду из глины. Форму глиняной лепешке придают вращением вокруг оси. Затем полученную форму обжигают. Это ремесло живо и по сей день. В различных районах Азербайджана есть ремесленники, которые изготавливают керамическую посуду. Исследуйте принцип работы по которому кусок глины приобретает какую-либо форму.
Плоские фигуры (плоская часть ограниченная кривой), совершая один полный оборот вокруг определенной оси, образуют пространственные фигуры. Эта ось называется осью вращении.
Цилиндр, конус и сфера являются простыми пространственными фигурами, полученными при вращении.
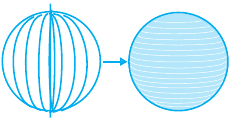
Например, при вращении прямоугольного треугольника вокруг одного из катетов получается конус, при вращении прямоугольника вокруг стороны образуется цилиндр, а при вращении полукруга вокруг диаметра — шар.
Цилиндр
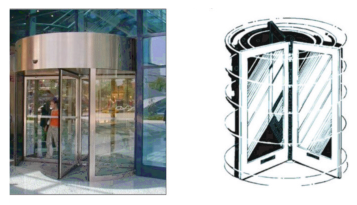
Наглядно образование фигур вращения можно увидеть на примере вращающихся стеклянных дверей, которые мы часто видим в общественных зданиях, отелях и больницах. Прямоугольный слой двери, прикрепленный к неподвижной стойке, при вращении очерчивает цилиндр.
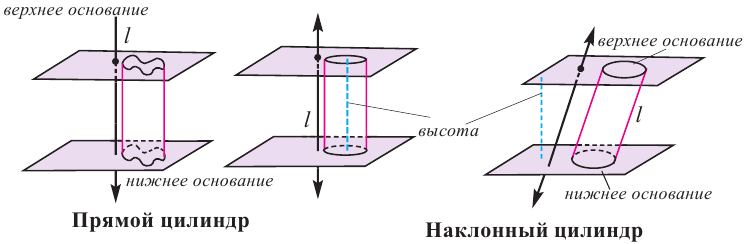
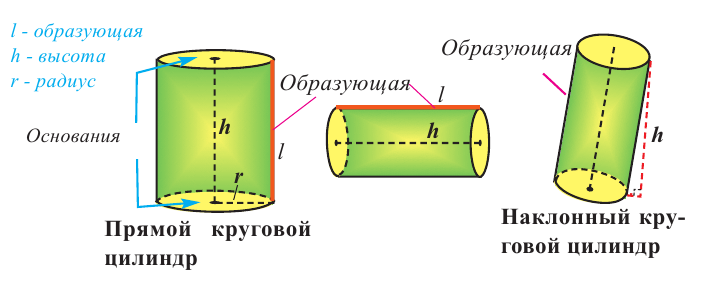
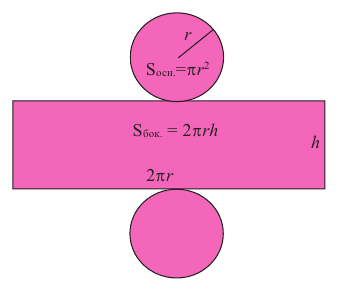
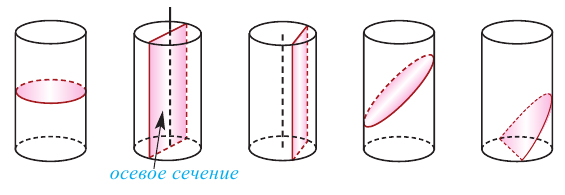
Цилиндром называется пространственная фигура, образованная двумя параллельными и конгруэнтными плоскими фигурами, которые совпадают при параллельном переносе, и отрезками, соединяющими соответствующие точки данных фигур. Плоские фигуры называются основаниями цилиндра, отрезки, соединяющие соответствующие точки основания называются образующими цилиндра. Если образующая перпендикулярна основанию, то цилиндр называется прямым, иначе — наклонным. Расстояние между основаниями называется высотой цилиндра.
На рисунках ниже изображены прямые и наклонные цилиндрические фигуры.
Сравнивая рисунки, изображенные ниже, можно сделать вывод, что призму можно рассматривать как частный случай цилиндра.
Прямой цилиндр, в основании которого лежит круг, называют прямым круговым цилиндром.
Далее, говоря о цилиндре, мы будем иметь в виду прямой круговой цилиндр. В любом другом случае будут отмечены его особенности.
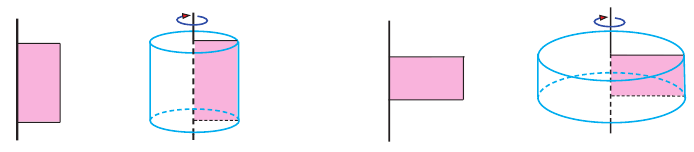
Прямой круговой цилиндр также можно рассматривать как фигуру, полученную вращением прямоугольника вокруг одной из его сторон. Высота прямого кругового цилиндра равна его образующей. Радиусом цилиндра называется радиус круга в основании.
Вращая прямоугольник вокруг любой стороны, можно получить цилиндр, высота которого равна стороне прямоугольника.
Прямая, проходящая через центры оснований прямого кругового цилиндра называется осью цилиндра.
Площадь поверхности цилиндра
Площадь боковой и полной поверхностей цилиндра.
Изобразите на листе бумаги рисунки разверток цилиндров различных размеров, вырежьте и склейте цилиндры.
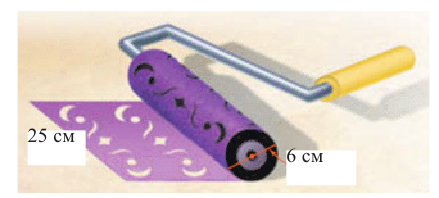
Мустафа красит стену цилиндрической кистью. Чтобы подсчитать время, потраченное на покраску, он захотел узнать, какую площадь покрывает кисть при одном полном обороте? Какие советы вы могли бы дать мальчику?
Так как кисть имеет цилиндрическую форму, то за один полный оборот кисть покрывает площадь в форме прямоугольника, равную боковой поверхности цилиндра.
Полная поверхность цилиндра находится но формуле схожей с формулой полной поверхности призмы. Полная поверхность цилиндра состоит из боковой поверхности и двух конгруэнтных кругов.
Боковую поверхность цилиндра с высотой 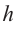
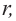
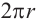
Боковая поверхность цилиндра равна произведению длины окружности основания и высоты.
Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей оснований
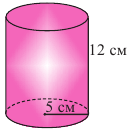
Пример №1
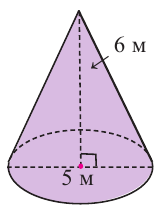
Найдите площадь полной поверхности цилиндра выстой 12 см и радиусом 5 см.
Решение:
Пример №2
По данным рисунка, найдите площадь боковой поверхности прямого цилиндра, основанием которой являются полукруг.
Решение:
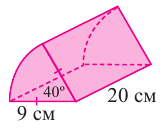
Пример №3
По данным на рисунке найдите площадь полной поверхности прямого цилиндра, основанием которой является круговой сектор с углом 40°.
Решение: известно, что
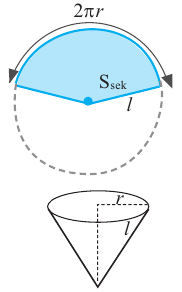
По формуле площади сектора:
Боковая поверхность фигуры равна 
Таким образом,
Конус
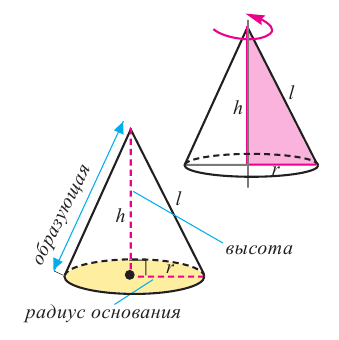
Конусом называется пространственная фигура, образованная всеми отрезками, соединяющими какую-либо плоскую фигуру с точкой, не принадлежащей данной плоскости. Плоскую фигуру называют основанием конуса, а точку —вершиной конуса.
Перпендикуляр, проведенный из вершины конуса на плоскость его основания, называется высотой конуса. Конус, в основании которого лежит круг, называется круговым конусом. Если ортогональная проекция вершины конуса лежит в центре основания, то конус называется прямым круговым конусом. Отрезок, соединяющий вершину конуса с любой точкой окружности основания кругового конуса, называется образующей конуса. В дальнейшем, говоря о конусе, будем иметь ввиду прямой круговой конус.
Конус можно рассматривать как фигуру, образованную вращением прямоугольного треугольника вокруг одного из катетов.
Прямая, выходящая из вершины конуса и проходящая через центр основания, называется осью конуса, радиус основания называется радиусом конуса. Для образующей, высоты и радиуса конуса справедливо отношение 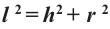
Сооружение конуса
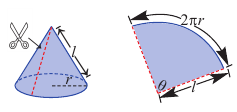
Известно, что при сворачивании прямоугольника можно получить цилиндр. Скручивая круговой сектор можно соорудить конус.
Радиус сектора равен образующей конуса, а длина дуги сектора равна длине окружности основания.
Боковая поверхность конуса, полная поверхность конуса
Поверхность конуса состоит из боковой поверхности и круга в основании. На рисунке показаны радиус основания 
Боковая поверхность конуса — круговой сектор с радиусом 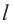
Значит, площадь сектора и есть площадь боковой поверхности.
Значит, сектор составляет 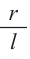
* Зная, что площадь круга 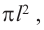
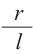
Значит,
Боковая поверхность конуса равна произведению половины длины окружности основания и образующей.
* Площадь полной поверхности конуса
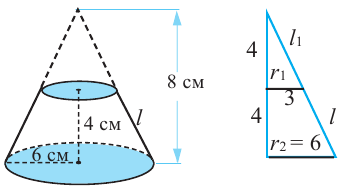
Пример №4
По рисунку найдите площадь боковой и полной поверхностей конуса.
Решение: Дано:
Найти: 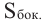
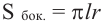
Чтобы найти образующую 
Сечения цилиндра и конуса плоскостью
Сечения поверхности конуса плоскостью (теория конических сечений) считались одной из вершин античной геометрии. Исследования Аполлония (3-й в.до н.э.) показали, что сечением плоскостью конуса, с бесконечной образующей (лучом) является: эллине (плоскость пересекает все образующие), парабола (плоскость сечения параллельна одной из образующих) или ветвь гиперболы (плоскость сечения параллельна двум образующим).
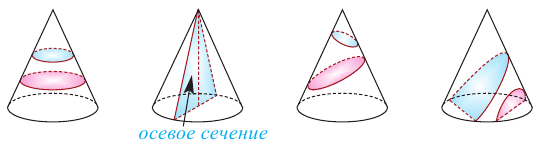
Сечения цилиндра плоскостью
Сечением цилиндра плоскостью, параллельной основанию, является круг. Сечение цилиндра плоскостью, проходящей через ось симметрии, называется осевым сечением. Осевое сечение цилиндра является прямоугольником со сторонами 
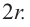
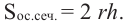
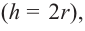
Сечения конуса плоскостью
Сечением конуса плоскостью, параллельной основанию, является круг. Сечение конуса, проходящее через ось конуса называется осевым сечением конуса. Это сечение является равнобедренным треугольником, боковые стороны которого являются образующими, а основание равно диаметру конуса: 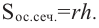
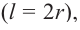
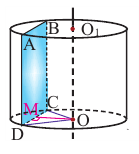
Пример №5
Сечением цилиндра плоскостью, проведенного параллельно оси цилиндра на расстоянии 3 см от оси, является квадрат, площадь которого равна 64 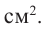
Решение: сначала найдем радиус и высоту цилиндра. По условию 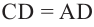
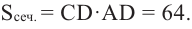
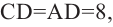
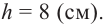
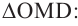
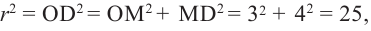
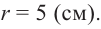
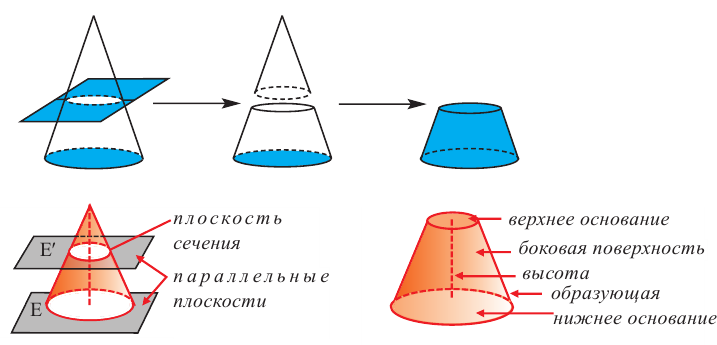
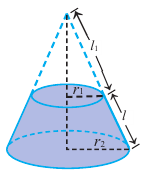
Усеченный конус и площадь поверхности
Усеченный конус
Если параллельно основанию прямого кругового конуса провести плоскость, то получим маленький конус и усеченный конус.
Усеченным конусом называется часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию.
Боковая поверхность усеченного конуса равна разности боковых поверхностей большого конуса и маленького конуса, отсеченного плоскостью, параллельной основанию, от большого конуса. Используя обозначения на рисунке, можно записать:
Из подобия треугольников запишем следующее отношение
Тогда, подставив 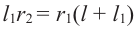
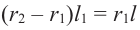
В данной формуле введем обозначение 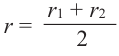
усеченного конуса. Тогда
Полная поверхность усеченного конуса равна сумме боковой поверхности и площадей нижнего и верхнего оснований.
Пример №6
Конус высотой 8 см и радиусом 6 см рассечен плоскостью, параллельной основанию. Высота полученного усеченного конуса равна 4 см. Найдите площади боковой и полной поверхностей усеченного конуса
Решение: дано:
Найти:
Площадь поверхности шара и его частей
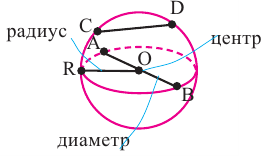
Шаром называется множество всех точек пространства находящихся от данной точки на расстоянии, не больше данного. Данная точка называется центром шара, данное расстояние радиусом 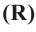
Множество всех точек, расположенных на расстоянии 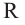
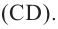
Шар получается, при вращении полукруга вокруг диаметра.
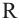
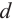
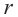
Пример №7
Шар радиуса 10 см пересечена плоскостью на расстояние
8 см от центра. Вычислите площадь сечения.
Решение: По условию
Тогда
Сечение шара плоскостью, проходящей через центр шара, называется
большим кругом. Центр, радиус и диаметр большого круга равны
центру, радиусу и диаметру шара.
Также для шара известны следующие части:
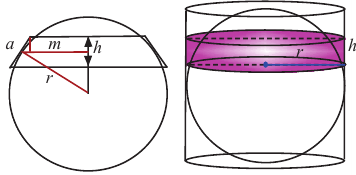
Площадь поверхности шара
Площадь поверхности шара находится по формуле 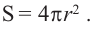
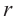
В окружность радиусом 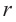
Покажем, что при вращении сторон многоугольника вокруг оси получается тело (конус, усеченный конус, цилиндр), площадь боковой поверхности которого равна площади боковой поверхности цилиндра, высота которого равна высоте данного тела, радиус основания равен апофеме многоугольника. Обозначим апофему многоугольника через
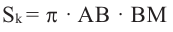
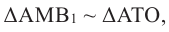
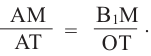
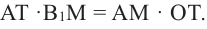
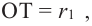
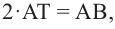
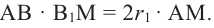
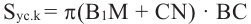
Зная, что 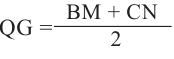
Так как 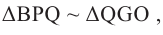
Умножим на 2 обе части равенства 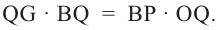
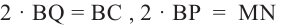
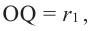
Значит,
Понятно, что площадь боковой поверхности цилиндра с образующей 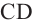
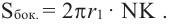
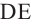
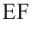
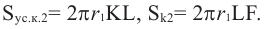
При бесконечном увеличении количества сторон многоугольника значение
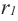
поверхности шара, т. е.
Площадь поверхности шара
Доказательство Архимеда:
Пусть, в правильный многоугольник вписан круг, как показано на рисунке.
При вращении получается шар и покрывающее шар тело
Это тело состоит из двух усеченных конусов и цилиндра.
При увеличении количества сторон до бесконечности, тело будет стремится принять форму шара.
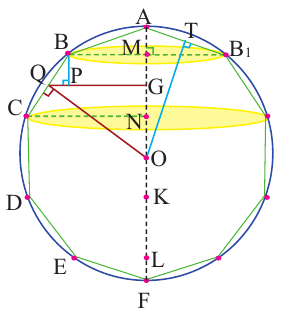
Найдя сумму поверхностей усеченных конусов и цилиндра, можно найти площадь поверхности шара. Рассмотрим осевое сечение одного из усеченных конусов. Пусть радиус средней окружности равен 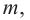
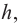
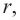
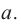
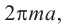
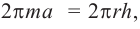
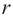
Значит, фигуру, описанную вокруг шара, можно принять за цилиндр. Отсюда получается, что площадь поверхности шара равна площади боковой поверхности цилиндра с радиусом основания 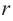
Т. е.,
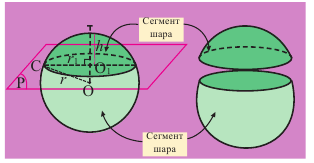
Площадь сегмента шара
Часть шара, отсекаемая плоскостью сечения называется сегментом. Круг, полученный при сечении плоскостью, называется основанием сегмента. Часть диаметра шара, перпендикулярного основанию сегмента, расположенная внутри него, называется высотой сегмента.
Из доказательства формулы поверхности шара, аналогично, можно показать, что для шара радиуса 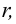
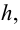
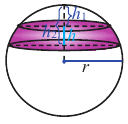
Площадь шарового пояса
Часть поверхности шара, расположенная между двумя параллельными плоскостями, называется шаровым поясом. Расстояние между параллельными плоскостями называется высотой шарового пояса.
Площадь поверхности шарового пояса можно найти, как разность площадей сегментов, отсекаемых параллельными плоскостями.
Площадь поверхности шарового пояса высотой 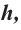
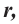
Пример №8
Радиус шара разбит на три равные части и через эти точки проведены перпендикулярные к радиусу плоскости. Зная, что радиус шара 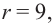
Решение: если 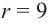
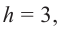
Площади поверхностей подобных фигур
Отношение соответствующих линейных размеров подобных пространственных фигур постоянно и равно коэффициенту подобия.
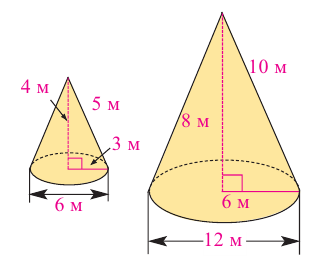
Например, чтобы проверить подобны ли конусы на рисунке, найдем отношение соответствующих размеров. Если эти конусы подобны, то отношение радиусов должно быть равно отношению высот.
Значит эти конусы подобны и коэффициент подобия равен 2. Это говорит о том, что если все линейные размеры маленького конуса пропорционально увеличить в два раза, то получим конус, конгруэнтный большому конусу. Или наоборот, пропорционально уменьшив размеры большого конуса в два раза, получим конус, конгруэнтный маленькому. Если пропорционально увеличить или уменьшить размеры какой-либо фигуры, то можно получить подобные фигуры.
Отношение площадей подобных фигур равно квадрату отношения соответствующих линейных размеров или квадрату коэффициента подобия
- Объем фигур вращения
- Длина дуги кривой
- Геометрические фигуры и их свойства
- Основные фигуры геометрии и их расположение в пространстве
- Вписанные и описанные многоугольники
- Площадь прямоугольника
- Объем пространственных фигур
- Объёмы поверхностей геометрических тел
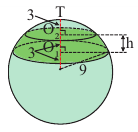
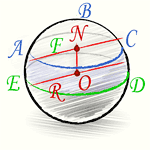
Площадь поверхности шарового слоя, формула
Шаровой слой — это часть шара, заключенная между двумя секущими параллельными плоскостями.
Шаровой пояс или Шаровая зона — это кривая поверхность шарового слоя. Круги ABC и DEF это основания шарового пояса. Расстояние между основаниями это высота шарового слоя.
Кривая поверхность шарового слоя равна произведению его высоты на окружность большого круга шара:
[ S = 2pi R h ]
(R — радиус большого круга шара, h=NO — высота шарового слоя)
Формулы шара, сферы
Вычислить, найти площадь поверхности шарового слоя по формуле (1)
Ссылки по теме
Площадь поверхности шарового слоя |
стр. 316 |
|---|
Как рассчитать площадь шарового слоя
На данной странице можно быстро и точно рассчитать площадь шарового слоя онлайн. Для этого нужно знать радиус и высоту.
На данной странице калькулятор поможет рассчитать площадь поверхности шарового слоя онлайн. Для расчета задайте радиус и высоту.
Шаровой слой — это часть шара, ограниченная двумя секущими параллельными плоскостями.
Через радиус и высоту
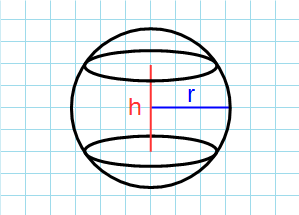
Формула площади шарового слоя через радиус и высоту:
π — константа равная (3.14); r — радиус шара; h — высота шарового сегмента.