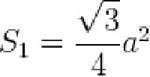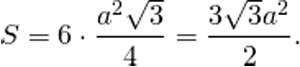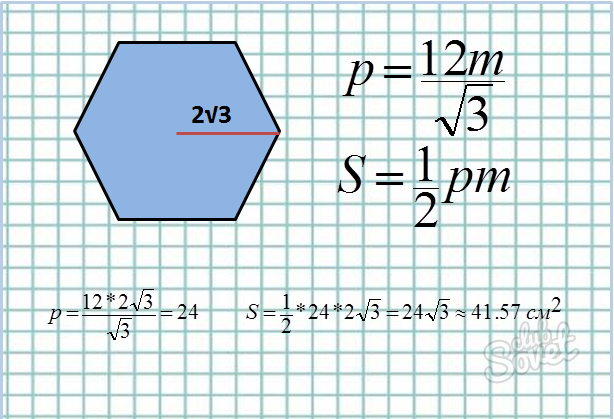Цель:
- Учить находить площадь плоской фигуры сложной конфигурации.
- Развивать конструктивное мышление.
- Воспитывать потребность к творческому отношению к делу.
Оборудование: карточки, компьютерная поддержка, линейки, карандаши, набор фигур.
Ход урока
I. Организационный момент
Учитель. Вдохновение нужно в геометрии не меньше, чем в поэзии. (А.С. Пушкин) (Слайд 1)
II. Геометрическая разминка
Решение кроссворда.
Учитель. Начнём урок с геометрической разминки. Решим кроссворд, который поможет нам определить тему урока. (Слайд 2)
- Запишите название фигуры. (Слайд 3)
- Определите по описанию название фигуры.
Попарно три прямых, пересекаясь,
Мне к трём углам дают три стороны.
По-разному всегда я называюсь,
Когда углы или стороны даны.
- Четырёхугольник, у которого все стороны равны.
- Название фигуры. (Слайд 4)
- Четырёхугольник, у которого все стороны равны и углы прямые.
- Четырёхугольник, у которого все углы прямые, а противоположные стороны равны.
Учитель. Мы записали названия фигур. По какому признаку можно разделить эти фигуры на две группы?
Дети. Геометрические фигуры бывают плоскими и пространственными. В первую группу войдут пространственные фигуры. Во вторую группу – плоские фигуры.
Учитель. Расскажите о пространственных фигурах. (Слайд 5)
Дети. Пространственные фигуры, не укладываются ни на какой плоскости, её точки все вместе не принадлежат никакой одной плоскости.
Учитель. Расскажите о плоских фигурах. (Слайд 6)
Дети. Плоская фигура укладывается на одной какой-нибудь плоскости, все её точки принадлежат этой плоскости.
Учитель. Вернёмся к кроссворду и прочитаем ключевое слово. (Площадь)
III. Сообщение темы урока
(Слайд 7)
Учитель. Площадь каких плоских фигур мы умеем находить?
Дети. Мы умеем находить площадь квадрата и прямоугольника.
Учитель. Как найти площадь прямоугольника?
Дети. Чтобы найти площадь прямоугольника, нужно длину умножить на ширину.
Учитель. Как найти площадь квадрата?
Дети. Нужно перемножить его стороны.
Учитель. Перед нами плоская фигура – шестиугольник. (Слайд 
Найдите площадь шестиугольника, выполнив необходимые измерения (дети работают с фигурой).
Дети. (см2)
Нужно шестиугольник мысленно разбить на две фигуры – треугольник и пятиугольник и дополнить его до квадрата. (Слайд 9)
IV. Практическая работа (дети разрезают шестиугольник на две фигуры).
Учитель. Как вы думаете, существуют ли другие способы решения этой задачи? Например, площадь данной фигуры можно найти, разбив её на три треугольника. И площадь шестиугольника будет равна сумме площадей трёх треугольников.
(Слайд 10)
V. Практическая работа (дети разрезают фигуру на три треугольника).
Учитель. Сравните треугольники. Чем они похожи? Какие это треугольники?
Дети. Это прямоугольные треугольники. Треугольник, у которого есть прямой угол, называют прямоугольным треугольником. (Cлайд11)
Учитель. Как найти площадь прямоугольного треугольника?
Дети. Нужно треугольник достроить до прямоугольника. Мы найдём площадь прямоугольника и поделим её пополам. (Слайд 12)
Учитель. Запишите решение.
(см2)
VI. Самостоятельная работа
Учитель. Умение находить площадь прямоугольного треугольника и прямоугольника позволяет находить площадь любого плоского многоугольника. В этом мы можем с вами убедиться в решении следующей задачи. (Cлайд 13)
Решение задачи
К прямоугольнику со сторонами 7 см и 5 см приложен прямоугольный треугольник со сторонами образующими прямой угол, равный 4 см и 5 см. Из получившегося многоугольника вырезали квадрат со сторонами 4 см.
Варианты чертежей (Слайд 14)
Решение с комментированием
(см2) – площадь прямоугольника.
(см2) – площадь прямоугольного треугольника.
(см2) – площадь всей фигуры.
(см2) – площадь квадрата.
(см2) – площадь фигуры.
VII. Домашнее задание
(Cлайд 15)
Учитель. Вашим домашним заданием будет найти площадь шестиугольника вторым способом, разбив его на три прямоугольных треугольника. Исследуйте ещё раз эту фигуру. Сравните полученные результаты.
VIII. Итог урока
(Слайд 16)
Учитель. И мы ещё раз сегодня на уроке подтвердили слова А.С. Пушкина, что вдохновение нужно в геометрии не меньше, чем в поэзии.
Оглавление:
- Площадь правильного шестиугольника
- Площадь неправильного шестиугольника
- Площадь равностороннего шестиугольника
Умение определять площадь различных фигур играет немалую
роль в жизни каждого человека. Рано или поздно приходится иметь дело с этими
знаниями. К примеру, в процессе ремонта помещения для определения необходимого
количества рулонов обоев, линолеума, паркета, плитки в ванную или на кухню
нужно уметь рассчитывать необходимую площадь.
Знаниями в области геометрии пользовались еще в древнем
Вавилоне и других странах. На первых шагах к культуре всегда возникала
необходимость измерить участок, расстояние. При строительстве первых
значительных сооружений требовались умения выдерживать вертикаль,
спроектировать план.
Роль эстетических потребностей людей также имела немалое
значение. Украшение жилища, одежды, рисование картин способствовало процессу
формирования и накопления сведений в области геометрии, которые люди тех времён
добывали опытным путем, по крупицам и передавали из поколения в поколение.
Сегодня знания геометрии необходимы и закройщику, и строителю,
и архитектору и каждому простому человеку в быту.
Поэтому нужно учиться рассчитывать площадь различных
фигур, и помнить, что каждая из формул может пригодиться впоследствии на
практике, в том числе, и формула правильного шестиугольника. Шестиугольником называется
такая многоугольная фигура, общее количество углов которой равно шести.
Площадь правильного шестиугольника
Правильным шестиугольником называют шестиугольную фигуру,
которая имеет равные стороны. Углы у правильного шестиугольника также между
собой равны.
В повседневной жизни мы часто можем встретить предметы,
имеющие форму правильного шестиугольника. Это и металлическая гайка, и ячейки
пчелиных сот, и структура снежинки. Шестиугольными фигурами отлично заполняются
плоскости. Так, например, при мощении тротуарной плитки мы можем наблюдать, как
плитка укладывается одна возле другой, не оставляя пустых мест.
Свойства
правильного шестиугольника
- Правильный шестиугольник всегда будет иметь равные углы,
каждый из которых составляет 120˚. - Сторона фигуры равняется радиусу описанной окружности.
- Все стороны в правильном шестиугольнике равны.
- Правильный шестиугольник плотно заполняет плоскость.
Как посчитать
площадь правильного шестиугольника?
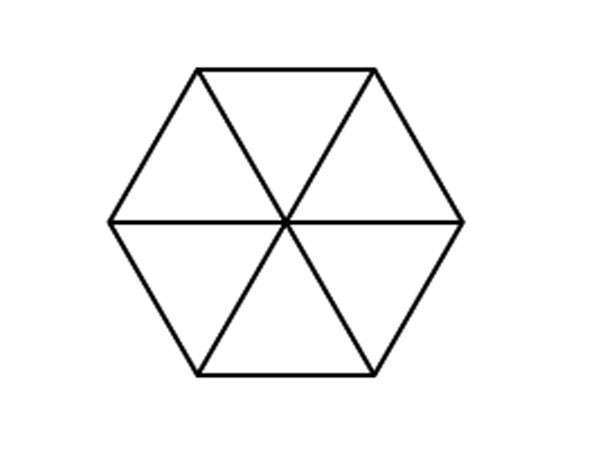
Площадь правильного шестиугольника можно рассчитать,
разбив его на шесть треугольников, каждый из которых будет иметь равные
стороны.
Для расчета площади правильного треугольника используется
следующая формула:
Зная площадь одного из треугольников, можно легко
рассчитать площадь шестиугольника. Формула для ее расчета проста: поскольку
правильный шестиугольник — это шесть равных треугольников, следует площадь
нашего треугольника умножить на 6.
Если провести от центра фигуры к любой из ее сторон
перпендикуляр, получим отрезок, который называется апофема. Рассмотрим, как
найти площадь шестиугольника при известной апофеме:
- Площадь = 1/2*периметр*апофему.
- Предположим, наша апофема равняется 5√3 см.
- Используя апофему, находим периметр: Поскольку апофема
расположена перпендикулярно к стороне шестиугольника, то углы треугольника,
созданного при помощи апофемы, будут равняться 30˚—60˚—90˚. Каждая сторона
полученного треугольника будет соответствовать: x-x√3-2x,
где короткая сторона, которая расположена напротив угла в 30˚— это x, длинная сторона,
расположенная напротив угла в 60˚ — это x√3,
а гипотенуза — 2x. - Поскольку апофема представлена, как x√3, можно подставить ее в формулу a = x√3 и решить. Если, к примеру,
апофема = 5√3, тогда подставим эту
величину в формулу и получим: 5√3 см = x√3, или x = 5
см. - Итак, короткая сторона треугольника равняется 5 см.
поскольку эта величина является половиной длины стороны шестиугольника,
умножаем 5 на 2 и получим 10 см, которая является длиной стороны. - Зная длину стороны, умножим её на 6 и получим периметр
шестиугольника:10 см х 6 = 60 см - Подставим полученные результаты в нашу формулу:
Площадь =
1/2*периметр*апофему
Площадь = ½*60см*5√3
Решаем:
Теперь осталось упростить
ответ, чтобы избавиться от квадратных корней, а полученный результат укажем в
квадратных сантиметрах:
½ * 60 см * 5√3 см =30 * 5√3
см =150 √3 см =259.8 см²
Видео о том, как найти площадь правильного шестиугольника
Площадь неправильного шестиугольника
Существует несколько вариантов определения площади
неправильного шестиугольника:
- Метод трапеции.
- Метод расчета площади неправильных многоугольников при
помощи оси координат. - Метод разбивания шестиугольника на другие фигуры.
В зависимости от исходных данных, которые вам будут
известны, подбирается подходящий метод.
Метод трапеции
Площадь шестиугольника, имеющего произвольную
(неправильную) форму, рассчитывается методом трапеции, суть которого состоит в
разделении шестиугольника на отдельные трапеции и последующим вычислением
площади каждой из них.
Метод с осями
координат
Кроме этого, площадь неправильного шестиугольника можно рассчитать
при помощи метода расчета площади неправильных многоугольников. Рассмотрим его
на следующем примере:
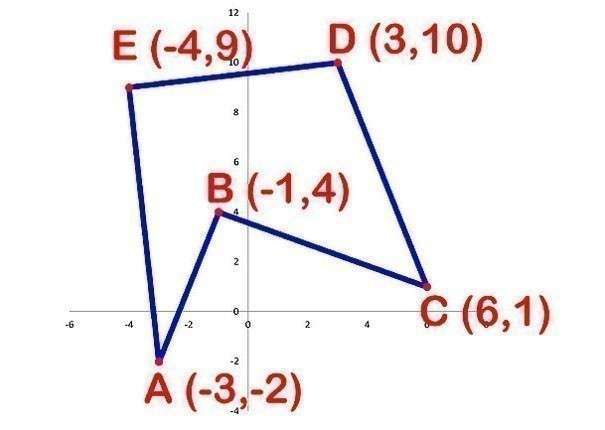
Вычисление будем выполнять методом использования
координат вершин многоугольника:
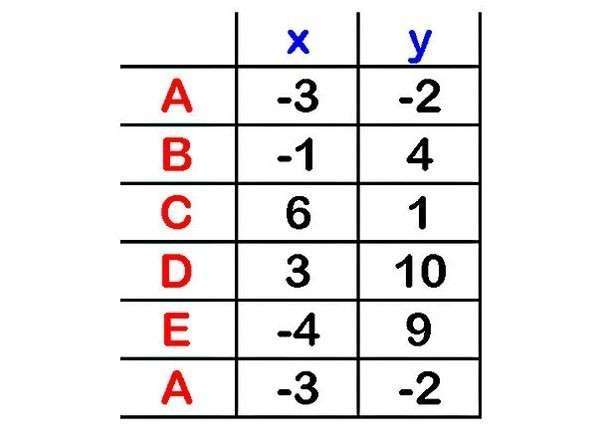
- На этом этапе следует сделать таблицу и записать
координаты вершин x и y. Выбираем вершины в
последовательном порядке по направлению против часовой стрелки, завершив конец
списка повторной записью координаты первой вершины:
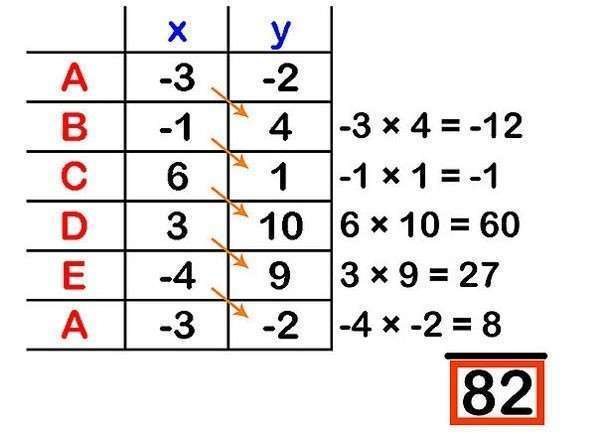
- Теперь следует умножить значения координаты х 1-й вершины
на y 2-й
вершины и продолжить таким образом умножение далее. Затем необходимо сложить
полученные результаты. В нашем случае получилось 82:
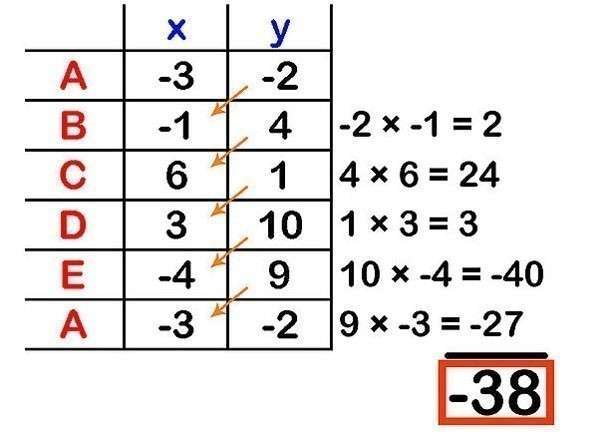
- Последовательно умножаем значения координат y1-й
вершины на значения координат х 2-й вершины. Суммируем полученные результаты. В
нашем случае получилось 38:
- Вычитаем сумму, которую получили на четвертом этапе из
суммы, которая получилась на третьем этапе: 82 – (-38) = 120
- Теперь необходимо разделить результат, который был
получен на предыдущем этапе и найдем площадь нашей фигуры: S= 120/2 = 60
см²
Метод разбивания
шестиугольника на другие фигуры
Каждый многоугольник можно разделить на несколько других
фигур. Это могут быть треугольники, трапеции, прямоугольники. Исходя из
известных данных, пользуясь формулами определения площадей перечисленных фигур,
последовательно вычисляются их площади и затем суммируются.
Некоторые неправильные шестиугольники состоят из двух
параллелограммов. Для определения площади параллелограмма следует умножить его
длину на ширину и затем сложить две уже известные площади.
Видео о том, как найти площадь многоугольника
Площадь равностороннего шестиугольника
Равносторонний шестиугольник имеет шесть равных сторон и
является правильным шестиугольником.
Площадь равностороннего шестиугольника равняется 6
площадям треугольников, на которые разбита правильная шестиугольная фигура.
Все треугольники в шестиугольнике правильной формы равны,
поэтому для нахождения площади такого шестиугольника достаточно будет знать
площадь хотя бы одного треугольника.
Для нахождения площади равностороннего шестиугольника
используется, конечно же, формула площади правильного шестиугольника, описанная
выше.
А Вы знали, как найти площадь шестиугольника? Как думаете, где эти знания пригодятся Вам в жизни? Поделитесь своим мнением в комментариях.
Как найти площадь шестиугольника
Шестиугольник – это многоугольник, имеющий 6 сторон и 6 углов. В зависимости от того, правильный шестиугольник или нет, существует несколько методов нахождения его площади. Мы рассмотрим все.
1
Как найти площадь правильного шестиугольника
Формулы для вычисления площади правильного шестиугольника – выпуклого многоугольника с шестью одинаковыми сторонами.
Дана длина стороны:
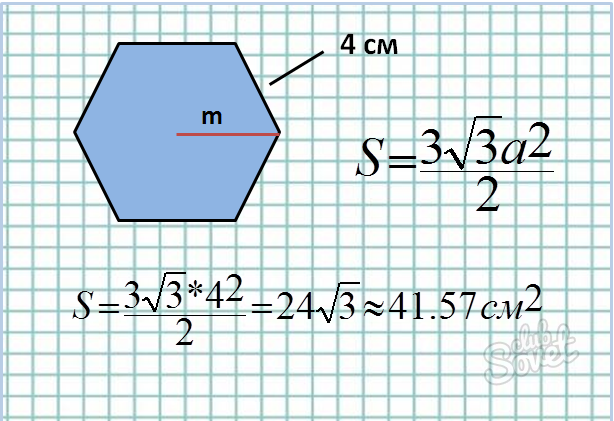
- Формула площади: S = (3√3*a²)/2
- Если длина стороны a известна, то подставив её в формулу, мы легко найдём площадь фигуры.
- В противном случае длину стороны можно найти через периметр и апофему.
- Если задан периметр, то мы просто делим его на 6 и получаем длину одной стороны. Например, если периметр равен 24, то длина стороны будет равняться 24/6 = 4.
- Апофема – перпендикуляр, проведённый из центра к одной из сторон. Чтобы найти длину одной стороны, подставляем длину апофемы в формулу а = 2*m/√3. То есть, если апофема m = 2√3, то длина стороны а = 2*2√3/√3 = 4.
Дана апофема:
- Формула площади: S = 1/2*p*m, где p – периметр, m – апофема.
- Найдём через апофему периметр шестиугольника. В предыдущем пункте мы научились находить длину одной стороны через апофему: а = 2*m/√3. Осталось только этот результат умножить на 6. Получаем формулу периметра: p = 12*m/√3.
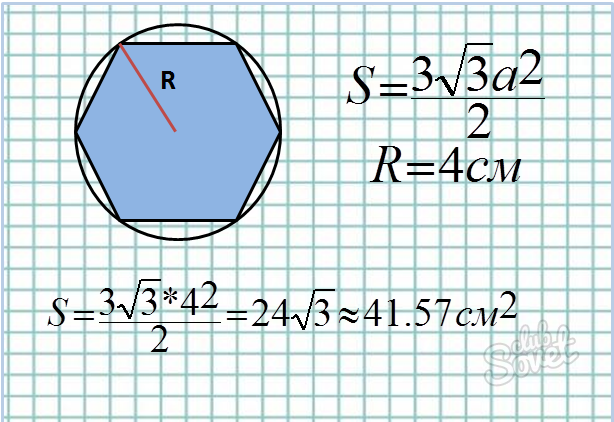
Дан радиус описанной окружности:
- Радиус описанной вокруг правильного шестиугольника окружности равен стороне этого шестиугольника.
Формула площади: S = (3√3*a²)/2
Дан радиус вписанной окружности:
- Формула площади: S = 3√3*r², где r = √3*a/2 (a – одна из сторон многоугольника).
2
Как найти площадь неправильного шестиугольника
Формулы для вычисления площади неправильного шестиугольника – многоугольника, стороны которого не равны между собой.
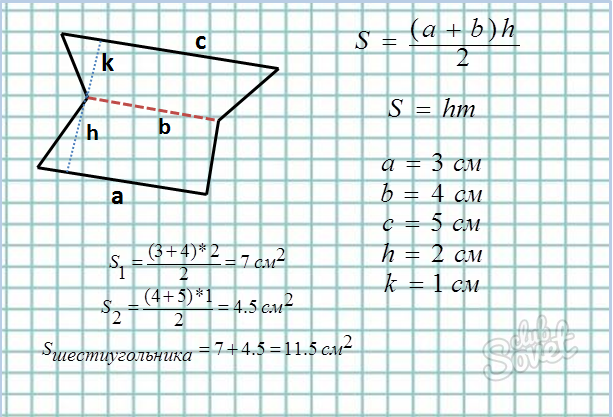
Метод трапеции:
- Делим шестиугольник на произвольные трапеции, вычисляем площадь каждой из них и складываем.
- Основные формулы площади трапеции: S = 1/2*(a + b)*h, где a и b – основания трапеции, h – высота.
S = h*m, где h – высота, m – средняя линия.
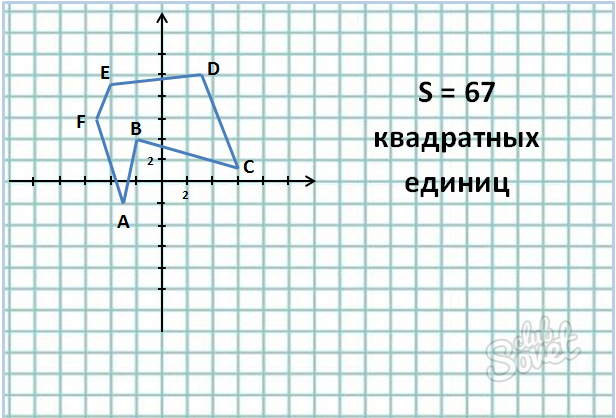
Известны координаты вершин шестиугольника:
- Для начала запишем координаты точек, причём, располагая их не в хаотичном порядке, а последовательно друг за другом. Например:
A: (-3, -2)
B: (-1, 4)
C: (6, 1)
D: (3, 10)
E: (-4, 9)
F: (-5, 6) - Далее, внимательно, умножаем координату x каждой точки на координату y следующей точки:
-3*4 = -12
-1*1 = -1
6*10 = 60
3*9 = 27
-4*6 = -24
-5*(-2) = 10
Результаты складываем:
-12 – 1 + 60 + 27 – 24 + 10 = 60
Далее умножаем координату y каждой точки на координату x следующей точки.
-2*(-1) = 2
4*6 = 24
1*3 = 3
10*(-4) = -40
9*(-5) = -45
6*(-3) = -18
Результаты складываем:
2 + 24 + 3 – 40 – 45 – 18 = -74
Из первого результата вычитаем второй:
60 -(-74) = 60 + 74 = 134
Полученное число делим на два:
134/2 = 67
Ответ: 67 квадратных единиц.
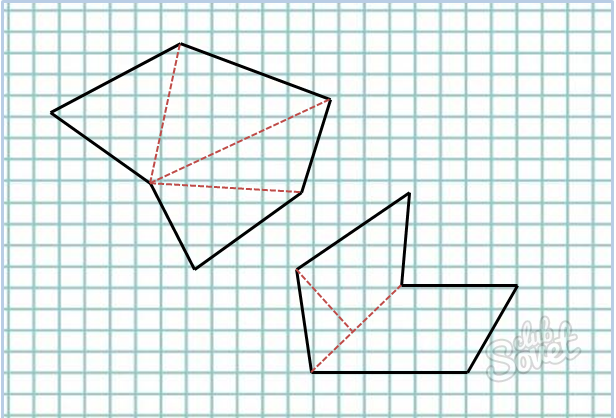
- Также для нахождения площади шестиугольника вы можете разбить его на треугольники, квадраты, прямоугольники, параллелограммы и так далее. Найти площади составляющих его фигур и сложить.
Итак, методы нахождения площади шестиугольника на все случаи жизни изучены. Теперь вперёд, применять полученные знания! Удачи!
На этой странице вы найдете калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного шестиугольника по стороне или радиусам вписанной и описанной окружностей.
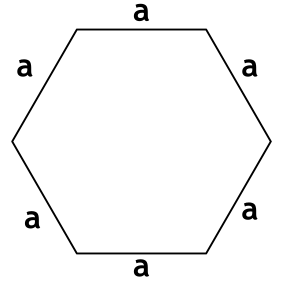
Шестиугольник представляет собой многоугольник, к которого все внутренние углы равны 120 градусов, а все стороны равны между собой.
Содержание:
- калькулятор площади правильного шестиугольника
- формула площади правильного шестиугольника через длину стороны
- формула площади правильного шестиугольника через радиус вписанной окружности
- формула площади правильного шестиугольника через радиус описанной окружности
- формула площади правильного шестиугольника через периметр
- примеры задач
Формула площади правильного шестиугольника через длину стороны
S = dfrac{3 sqrt{3} a^2}{2}
a — длина стороны шестиугольника
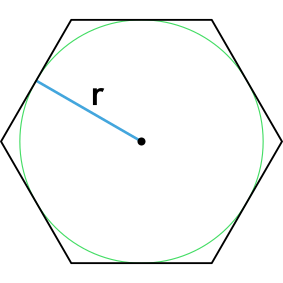
Формула площади правильного шестиугольника через радиус вписанной окружности
S = 2 sqrt{3}r^2
r — радиус вписанной окружности
Формула площади правильного шестиугольника через радиус описанной окружности
S = dfrac{3 sqrt{3} R^2}{2}
R — радиус описанной окружности
Формула площади правильного шестиугольника через периметр
S = dfrac{P^2 sqrt{3}}{24}
P — периметр шестиугольника
Примеры задач на нахождение площади правильного шестиугольника
Задача 1
Найдите площадь правильного шестиугольника, радиус вписанной окружности которого равен 9 см.
Решение
Исходя из того, что из условия задачи нам известен радиус вписанной окружности, мы воспользуемся формулой.
S = 2 sqrt{3}r^2 = 2 sqrt{3} cdot 9^2 = 2 sqrt{3} cdot 81 = 162 sqrt{3} : см^2 approx 280.59223 : см^2
Ответ: 162 sqrt{3} : см^2 approx 280.59223 : см^2
Проверить правильность решения нам поможет калькулятор .
Задача 2
Найдите площадь правильного шестиугольника со стороной равной 1 см.
Решение
Для этой задачи нам подойдет формула.
S = dfrac{3 sqrt{3} a^2}{2} = dfrac{3 sqrt{3} cdot 1^2}{2} = dfrac{3 sqrt{3} cdot 1}{2} = dfrac{3 sqrt{3}}{2} : см^2 approx 2.59808 : см^2
Ответ: dfrac{3 sqrt{3}}{2} : см^2 approx 2.59808 : см^2
Проверим ответ .
Как рассчитать площадь правильного шестиугольника
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник — многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
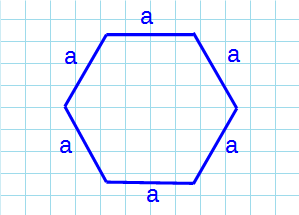
a:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через сторону:
a — сторона шестиугольника.
Через радиус описанной окружности
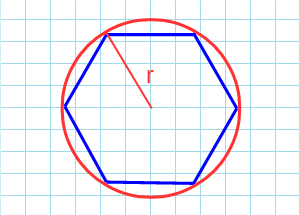
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
r — радиус описанной окружности.
Через радиус вписанной окружности
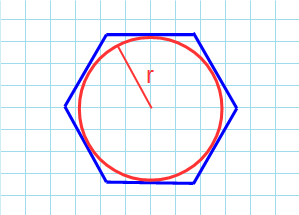
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности:
r — радиус вписанной окружности.