На этой странице вы найдете калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного шестиугольника по стороне или радиусам вписанной и описанной окружностей.
Шестиугольник представляет собой многоугольник, к которого все внутренние углы равны 120 градусов, а все стороны равны между собой.
Содержание:
- калькулятор площади правильного шестиугольника
- формула площади правильного шестиугольника через длину стороны
- формула площади правильного шестиугольника через радиус вписанной окружности
- формула площади правильного шестиугольника через радиус описанной окружности
- формула площади правильного шестиугольника через периметр
- примеры задач
Формула площади правильного шестиугольника через длину стороны
S = dfrac{3 sqrt{3} a^2}{2}
a — длина стороны шестиугольника
Формула площади правильного шестиугольника через радиус вписанной окружности
S = 2 sqrt{3}r^2
r — радиус вписанной окружности
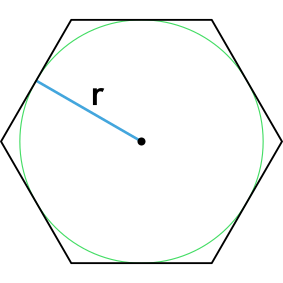
Формула площади правильного шестиугольника через радиус описанной окружности
S = dfrac{3 sqrt{3} R^2}{2}
R — радиус описанной окружности
Формула площади правильного шестиугольника через периметр
S = dfrac{P^2 sqrt{3}}{24}
P — периметр шестиугольника
Примеры задач на нахождение площади правильного шестиугольника
Задача 1
Найдите площадь правильного шестиугольника, радиус вписанной окружности которого равен 9 см.
Решение
Исходя из того, что из условия задачи нам известен радиус вписанной окружности, мы воспользуемся формулой.
S = 2 sqrt{3}r^2 = 2 sqrt{3} cdot 9^2 = 2 sqrt{3} cdot 81 = 162 sqrt{3} : см^2 approx 280.59223 : см^2
Ответ: 162 sqrt{3} : см^2 approx 280.59223 : см^2
Проверить правильность решения нам поможет калькулятор .
Задача 2
Найдите площадь правильного шестиугольника со стороной равной 1 см.
Решение
Для этой задачи нам подойдет формула.
S = dfrac{3 sqrt{3} a^2}{2} = dfrac{3 sqrt{3} cdot 1^2}{2} = dfrac{3 sqrt{3} cdot 1}{2} = dfrac{3 sqrt{3}}{2} : см^2 approx 2.59808 : см^2
Ответ: dfrac{3 sqrt{3}}{2} : см^2 approx 2.59808 : см^2
Проверим ответ .
Как рассчитать площадь правильного шестиугольника
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник — многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
a:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через сторону:
a — сторона шестиугольника.
Через радиус описанной окружности
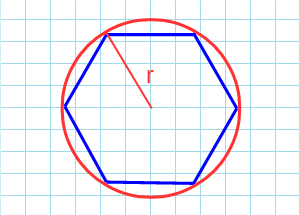
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
r — радиус описанной окружности.
Через радиус вписанной окружности
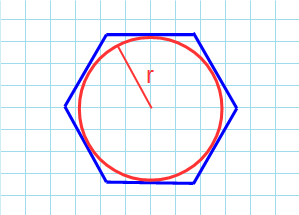
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности:
r — радиус вписанной окружности.
Калькулятор
Шестиугольник — многоугольник, у которого есть шесть сторон и шесть углов. В правильном заданном
многоугольном геометрическом объекте все стороны равняются друг другу, а углы формируют шесть
равносторонних треугольников.
Площадь правильной фигуры с шестью углами — положительная величина некоторой области плоскости,
занимаемой данным многоугольным геометрическим объектом.
Выделяют ряд методов нахождения площади этого многоугольника, зависимо от его типа.
- Площадь правильного шестиугольника через длину стороны
- Площадь правильного шестиугольника через радиус описаной окружности
- Площадь правильного шестиугольника через радиус вписаной окружности
- Площадь правильного шестиугольника через длинную диагональ
- Площадь правильного шестиугольника через короткую диагональ
- Площадь правильного шестиугольника через периметр
Через длину стороны
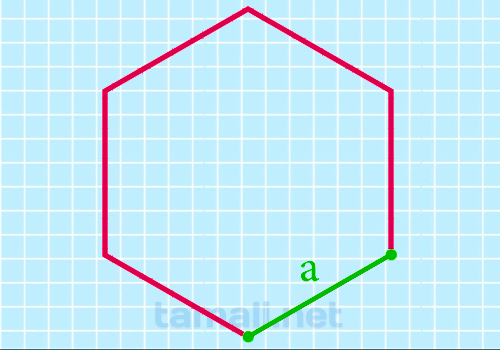
По той причине, что выпуклый шестиугольник включает в себя шесть равносторонних треугольников, тогда
формула нахождения требуемой величины через длину стороны выглядит следующим образом:
S = (3√3*a²)/2
где a — это продолжительность стороны.
Цифр после запятой:
Результат в:
Рассмотрим пример. Пусть длина стороны эквивалентна 8. Тогда, согласно этой формуле, заданную
характеристику замкнутого выпуклого шестиугольника будет примерно равна 166.
Всё достаточно
просто, если сторона заранее известна. Если же эта величина нам не дана, но известен периметр или
апофема — высота одного из шести равносторонних треугольников — тогда длину стороны можно
высчитать.
В случае, если известен периметр, его необходимо поделить на шесть, таким образом получается длина
стороны. К примеру, если периметр равен 36, то, поделив 36 на 6, получается 6 — это и есть
протяжённость стороны.
Если известна лишь апофема, тогда можно посчитать длину стороны, подставив апофему в формулу b = x√3 и умножив ответ на 2. Всё это потому, что апофема — это сторона
x√3 составляемого ей треугольника с углами 30, 60 и 90 градусов. К примеру, если апофема 11√3, то
x = 11, а протяжённость стороны будет эквивалентна 22.
Через периметр
Если при изучении правильной фигуры с шестью углами нам известен только его периметр, несложно
рассчитать площадь этой фигуры по такой формуле:
Цифр после запятой:
Результат в:
S = (3√3*(p/6)²)/2
где p — это периметр фигуры.
Допустим, если периметр будет равняться 24, тогда площадь будет примерно эквивалентна 42. Если в
качестве периметра возьмём число 50, тогда площадь фигуры окажется 180.
Через длинную диагональ
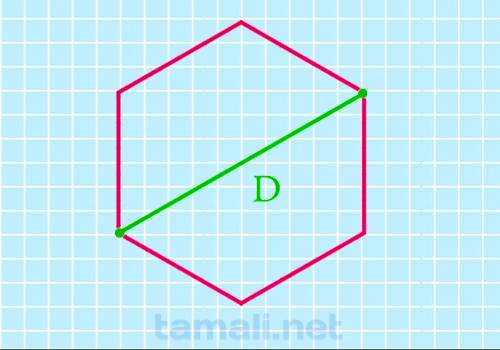
Длинная или большая диагональ шестиугольника — это диаметр описанной вокруг него плоской кривой, как
правило, она равняется двум его сторонам.
Цифр после запятой:
Результат в:
Используем такое выражение для подсчёта площади подобного правильного многоугольного геометрического
объекта через длинную диагональ этого множества точек:
S = (3√3*D²)/8
где D — это длинный отрезок, соединяющий несмежные вершины.
К примеру, если D = 6, тогда заданная характеристика замкнутого выпуклого
многоугольника будет приблизительно равна 23. Если в качестве длинной диагонали возьмём 8, тогда
величина будет примерно эквивалентна 42.
Через короткую диагональ
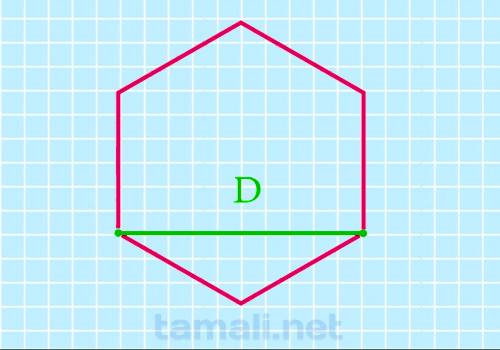
Меньшая или короткая диагональ правильного шестиугольника в √3 раз длиннее его стороны, также она
образует с ней прямой угол.
Цифр после запятой:
Результат в:
Если известна короткая диагональ такого выпуклого многоугольника, то с её помощью можно найти площадь
этой фигуры следующим образом:
S = (√3*D²)/2
где D — это протяжённость короткого отрезка, соединяющего несмежные
вершины.
К примеру, если длина такой диагонали будет равна 14, тогда необходимая характеристика фигуры будет
примерно равняться 170. Если же в качестве D мы возьмём 2, тогда величина
окажется всего лишь 3.
Через радиус описанной окружности
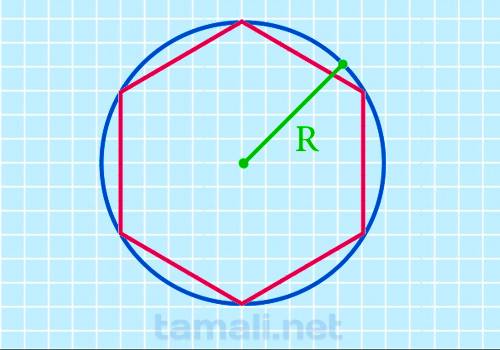
Шестиугольник считается правильным многоугольником, ведь все его стороны и углы эквивалентны друг
другу. Соответственно, около такого многоугольника можно описать окружность.
Чтобы найти площадь выпуклого многоугольника через радиус описанной окружности, необходимо
воспользоваться такой формулой:
S = (3√3*R²)/2
где R — это отрезок, соединяющий центр и любую точку описанной замкнутой
плоской кривой.
Цифр после запятой:
Результат в:
К примеру, если отрезок, соединяющий центр и любую точку, равняется 5, тогда заданная характеристика
замкнутой фигуры будет примерно равна 65. Если же в качестве радиуса возьмём число 12,
соответственно, заданная характеристика замкнутой фигуры получится примерно 374.
Через радиус вписанной окружности
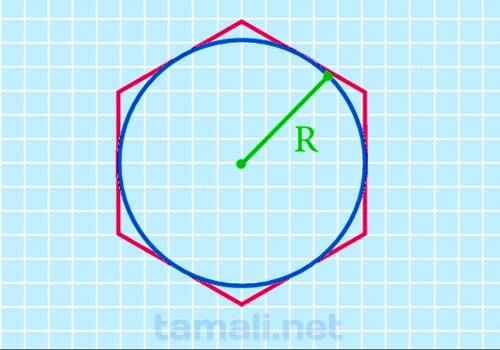
Шестиугольник считается правильным многоугольником, ведь все его стороны и углы равны друг другу.
Соответственно, во всякий шестиугольник можно вписать окружность.
Формула для расчёта площади следующего выпуклой фигуры с шестью углами через радиус вписанной
окружности будет выглядеть следующим образом:
S = √3*r²
где r — это отрезок, соединяющий центр и любую точку вписанной замкнутой
плоской кривой.
Цифр после запятой:
Результат в:
К примеру, если этот отрезок, соединяющий центр и любую точку, равен 14, тогда необходимая величина
этого множества точек будет примерно равна 679. Если в качестве отрезка, соединяющего центр и любую
точку, возьмем 4, тогда площадь будет приблизительно равна 55.
Что такое правильный шестиугольник
Этот многоугольный геометрический объект имеет определённые свойства:
- Каждый угол этой фигуры равняется 120 градусам;
- Вокруг правильного шестиугольника можно описать окружность, причем единственную, а её радиус
равняется его стороне; - Большие диагонали такого выпуклого многоугольника разделяют его на шесть равносторонних
треугольников, высота каждого равняется радиусу вписанной в выпуклый многоугольник окружности; - Центры вписанной и описанной окружностей около подобного выпуклого многоугольника — это точка
пересечения больших диагоналей этого множества точек.
Эта фигура очень часто встречается в природе, технике и культуре. К примеру:
- Пчелиные соты изображают разделение плоскости на выпуклые шестиугольники;
- Некоторые сложные молекулы углерода имеют гексагональную кристаллическую решётку;
- Сечение гайки и большинства карандашей описывается таким выпуклым многоугольником;
- Гексаграмма — это шестиконечная звезда, сформированная двумя правильными треугольниками. Также
её называют звездой Давида, она считается символом иудаизма.
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое правильный шестиугольник?
Правильный шестиугольник — это геометрическая фигура, которая является одним из типов правильных многоугольников. Он имеет шесть равных сторон и шесть равных углов. В правильном шестиугольнике все стороны равны между собой, и все углы равны 120 градусам.
Свойства правильного шестиугольника:
- Равные стороны. Все шесть сторон правильного шестиугольника имеют одинаковую длину.
- Равные углы. Каждый угол в правильном шестиугольнике равен 120 градусам.
- Центральная симметрия. Правильный шестиугольник обладает центральной симметрией, что означает, что его можно повернуть на 60 градусов вокруг центра так, чтобы он выглядел идентично.
- Описанная окружность. Центры описанной окружности правильного шестиугольника и самого шестиугольника совпадают.
По какой формуле калькулятор рассчитывает площадь правильного шестиугольника?
Калькулятор площади правильного шестиугольника — это онлайн инструмент, предназначенный для быстрого и удобного вычисления площади данного геометрического объекта. Он использует математическую формулу, специально разработанную для расчета площади правильного шестиугольника.
Формула для вычисления площади правильного шестиугольника выглядит следующим образом:
Площадь = (3 * √3) * (сторона^2) / 2
где «сторона» обозначает длину каждой стороны правильного шестиугольника.
Расчет производится следующим образом:
- Возведение длины стороны в квадрат (сторона^2).
- Умножение полученного значения на 3 и затем на квадратный корень из 3 (3 * √3).
- Деление полученного значения на 2 ((3 * √3) * (сторона^2) / 2).
Где и как можно использовать шестиугольник?
Шестиугольник может быть применен в различных областях и имеет множество применений. Вот некоторые из них:
- Архитектура и строительство. Шестиугольники могут использоваться в архитектуре для создания уникальных фасадов зданий или в планировке помещений. Например, шестиугольные плитки могут использоваться для создания интересных и гармоничных дизайнов пола и стен.
- Упаковка. Шестиугольные упаковочные контейнеры могут обеспечивать более эффективное использование пространства и обеспечивать прочность и стабильность конструкции.
- Биология и природа. Многие ячейки и пчелиные соты имеют форму шестиугольника, поскольку это оптимальная форма для заполнения пространства с минимальными затратами энергии. Также шестиугольники можно найти в структурах медовых трутней и в некоторых природных образованиях, таких как гексагональные базальтовые колонны.
- Геометрические и математические исследования. Шестиугольники являются одним из простейших правильных многоугольников, и их свойства широко изучаются в математике и геометрии. Они могут использоваться в качестве примеров для изучения углов, сторон и свойств многоугольников в целом.
- Графика и дизайн. Шестиугольники могут быть использованы в графическом дизайне и создании паттернов. Их регулярная форма и симметрия позволяют создавать интересные и гармоничные композиции.
- Игры и головоломки. Шестиугольники могут использоваться в играх и головоломках, где требуется решать задачи, связанные с их свойствами и геометрией.
Это лишь некоторые примеры применения шестиугольника. Фактически, шестиугольник может использоваться везде, где требуется регулярная форма с определенными свойствами и характеристиками.
Пример
Представим ситуацию, в которой вам необходимо покрыть пол шестиугольной комнаты плитками. Для этого вы хотите вычислить площадь правильного шестиугольника, чтобы определить количество плиток, которое вам потребуется для покрытия пола.
Предположим, что сторона вашего правильного шестиугольника равна 4 метра. Теперь, чтобы вычислить площадь, воспользуемся формулой для площади правильного шестиугольника:
Площадь = (3 * √3) * (сторона^2) / 2
Подставим значения:
Площадь = (3 * √3) * (4^2) / 2
Площадь = (3 * √3) * 16 / 2
Площадь = (3 * √3) * 8
Площадь = 24 * √3
Таким образом, площадь вашего правильного шестиугольника составляет 24 * √3 квадратных метра.
Теперь, если вы хотите вычислить количество плиток, которое вам потребуется для покрытия пола, вам нужно знать размер одной плитки. Предположим, что размер плитки составляет 0,25 квадратных метра.
Для вычисления количества плиток, поделите общую площадь пола на площадь одной плитки:
Количество плиток = Площадь пола / Площадь одной плитки
Количество плиток = (24 * √3) / 0,25
Вычислим это:
Количество плиток = 96 * √3
Таким образом, вам потребуется 96 * √3 (приблизительно, 166.286) плиток размером 0,25 квадратных метра для покрытия пола шестиугольной комнаты со стороной 4 метра.
Вычисление площади правильного шестиугольника может быть полезно при планировании различных проектов, таких как покрытие пола, расстановка мебели, зонирование пространства или расчет необходимого материала для строительства или ремонта.
❓ Вопросы и ответы
Сейчас мы предлагаем вам посмотреть ответы на вопросы, которые часто задаются на данную тему.
Что такое правильный шестиугольник?
Правильный шестиугольник — это многоугольник, у которого все стороны имеют одинаковую длину, а все углы равны 120 градусам.
Как вычислить площадь правильного шестиугольника?
Площадь правильного шестиугольника можно вычислить, используя формулу: Площадь = (3 * √3) * (сторона^2) / 2, где сторона — длина одной стороны шестиугольника.
Могу ли я использовать калькулятор площади правильного шестиугольника для десятичных значений сторон?
Да, вы можете использовать калькулятор площади правильного шестиугольника для десятичных значений сторон. Он примет любые числовые значения и вычислит площадь соответствующего правильного шестиугольника.
Как могу использовать площадь правильного шестиугольника на практике?
Площадь правильного шестиугольника может быть использована при проектировании различных объектов и структур, таких как крыши, мозаики, участки земли, полы, фасады зданий и другие. Вычисление площади поможет вам определить необходимое количество материалов, бюджет, площадь покрытия и другие аспекты проекта.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
В публикации представлены онлайн-калькуляторы и формулы, позволяющие вычислить площадь правильного шестиугольника через длину его стороны или радиус описанной окружности.
Содержание
скрыть
-
Расчет площади
- Через сторону
- Через радиус описанной окружности
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.
Через сторону
Формула расчета
Через радиус описанной окружности
Формула расчета