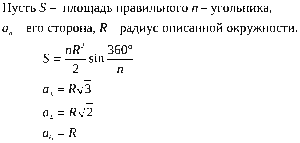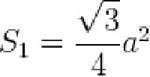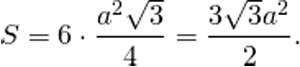С вопросом: «Как найти площадь шестиугольника?», можно столкнуться не только на экзамене по геометрии и т.п., эти знания пригодятся и в быту, например, для правильного и точного вычисления площади помещения в процессе ремонта. Подставив в формулу требуемые значения, получится определить нужное количество рулонов обоев, плитки в ванную или на кухню и т.д.
Содержание:
- Немного фактов из истории
- Площадь правильного 6-угольника
- Расчет
- Как находить площадь неправильного шестиугольника
- Метод трапеции
- Использование осей координат
- Разбивка шестиугольника на другие фигуры
- Площадь равностороннего шестиугольника
Немного фактов из истории
Геометрия использовалась еще в древнем Вавилоне и прочих государствах, существовавших в одно время с ним. Вычисления помогали при возведении значительных сооружений, так как благодаря ей зодчие знали как выдержать вертикаль, правильно составить план, определить высоту.
Эстетика тоже имела большое значение, и здесь снова шла в ход геометрия. Сегодня этой науки нужны строителю, закройщику, архитектору, да и не специалисту тоже.
Поэтому лучше уметь рассчитывать S фигур, понимать, что формулы могут пригодиться на практике.
Площадь правильного 6-угольника
Итак, у нас шестиугольная фигура с равными сторонами и углами. В повседневности мы часто имеем возможность встретить предметы правильной шестиугольной формы.
К примеру:
- гайка;
- пчелиные соты;
- снежинка.
Шестиугольная фигура наиболее экономично заполняет пространство на плоскости. Взгляните на тротуарную плитку, одна подогнана к другой так, что зазоров не остается.
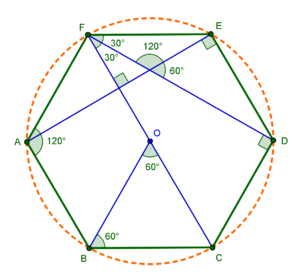
Каждый угол равен 120˚. Сторона фигуры равна радиусу описанной окружности.
Расчет
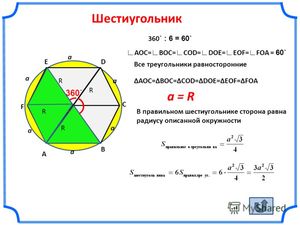
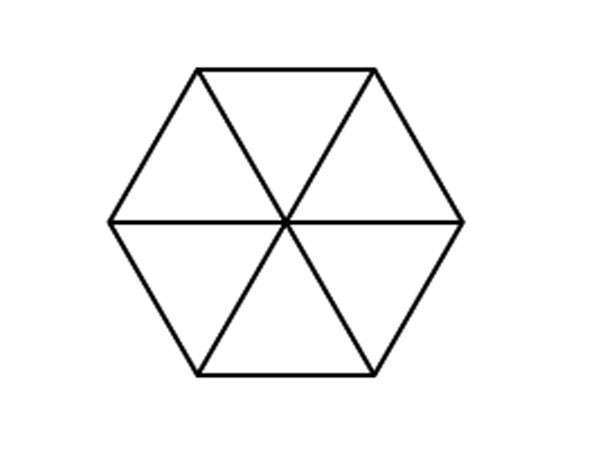
Требуемое значение можно вычислить, разбив фигуру на шесть треугольников с равными сторонами.
Чтоб рассчитать S , пользуются следующей формулой:
Вычислив S одного из треугольников, нетрудно определить и общую. Простая формула, так как правильный шестиугольник, по сути, является шестью равными треугольниками. Таким образом, для ее расчета найденную площадь одного треугольника умножают на 6.
Если от центра шестиугольника к любой его стороне провести перпендикуляр, получается отрезок – апофема.
Посмотрим, как находить S шестиугольника, если апофема известна:
- S =1/2×периметр×апофема.
- Возьмем апофему равную 5√3 см.
- Находим периметр, используя апофему: так как апофема перпендикулярно к стороне 6-угольника, углы треугольника, образованного с помощью апофемы, равняются 30˚-60˚-90˚. Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза — 2x.
- Апофему x√3 можно подставить в формулу a=x√3. Если апофема равна 5√3, подставив данную величину, получим: 5√3см=x√3, или x=5см.
- Короткая сторона треугольника составляет 5см, так как эта величина – половина длины стороны 6-угольника. Умножив 5 на 2, получим 10см, что есть значение длиной стороны.
- Полученную величину умножим на 6 и получим значение периметра – 60см.
Подставляем полученные результаты в формулу: S=1/2×периметр×апофема
S=½×60 см× 5√3
Считаем:
Упрощаем полученный ответ, чтоб избавиться от корней. Результат будет выражен в квадратных сантиметрах: ½×60см×5√3см=30×5√3см=150 √3см=259,8с м².
Как находить площадь неправильного шестиугольника
Есть несколько вариантов:
- Разбивка 6-угольника на другие фигуры.
- Метод трапеции.
- Расчет S неправильных многоугольников с помощью осей координат.
Выбор способа диктуется исходными данными.
Метод трапеции
Шестиугольник делится на отдельные трапеции, после чего вычисляется площадь каждой полученной фигуры.
Использование осей координат
Используем координаты вершин многоугольника:
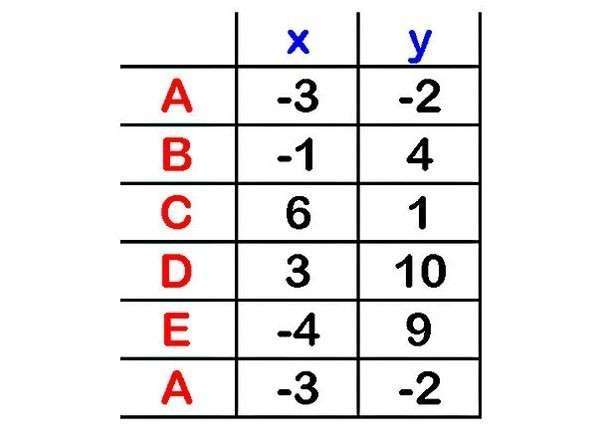
- В таблицу записываем координаты вершин x и y . Последовательно выбираем вершины, «двигаясь» против часовой стрелки, завершая список повторной записью координат первой вершины.
- Умножаем значения координаты x 1-й вершины на значение y 2-й вершины, и продолжаем так умножать. Складываем полученные результаты.
- Значения координат y1-й вершины умножаем на значения координат x 2-й вершины. Складываем результаты.
- Вычитаем сумму, полученную на 4-м этапе из суммы, полученной на третьем этапе.
- Делим результат, полученный на предыдущем этапе, и находим, что искали.
Разбивка шестиугольника на другие фигуры
Многоугольники разбиваются на другие фигуры: трапеции, треугольники, прямоугольники. Пользуясь формулами вычисления площадей перечисленных фигур, требуемые значения вычисляются и складываются.
Неправильный шестиугольник может состоять из двух параллелограммов. Чтоб вычислить площадь параллелограмма, его длина умножается на его ширину, а далее уже известные две площади складываются.
Площадь равностороннего шестиугольника
У правильного шестиугольника шесть равных сторон. Площадь равносторонней фигуры равна 6S треугольников, на которые разбит правильный шестиугольник. Каждый треугольник в правильном шестиугольнике равен, поэтому для вычисления площади такой фигуры довольно знать площадь хотя б одного треугольника.
Чтоб найти искомое значение пользуются формулой площади правильной фигуры, описанной выше.
Как высчитать площадь шестиугольника. Как найти площадь шестиугольника
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны
.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
Где — сторона правильного шестиугольника.
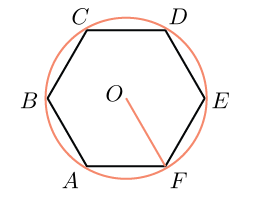
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне
.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
Ответ: .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Шестиугольник – это многоугольник, имеющий 6 сторон и 6 углов. В зависимости от того, правильный шестиугольник или нет, существует несколько методов нахождения его площади. Мы рассмотрим все.
Как найти площадь правильного шестиугольника
Формулы для вычисления площади правильного шестиугольника – выпуклого многоугольника с шестью одинаковыми сторонами.
Дана длина стороны:
- Формула площади: S = (3√3*a²)/2
- Если длина стороны a известна, то подставив её в формулу, мы легко найдём площадь фигуры.
- В противном случае длину стороны можно найти через периметр и апофему.
- Если задан периметр, то мы просто делим его на 6 и получаем длину одной стороны. Например, если периметр равен 24, то длина стороны будет равняться 24/6 = 4.
- Апофема – перпендикуляр, проведённый из центра к одной из сторон. Чтобы найти длину одной стороны, подставляем длину апофемы в формулу а = 2*m/√3. То есть, если апофема m = 2√3, то длина стороны а = 2*2√3/√3 = 4.
Дана апофема:
- Формула площади: S = 1/2*p*m, где p – периметр, m – апофема.
- Найдём через апофему периметр шестиугольника. В предыдущем пункте мы научились находить длину одной стороны через апофему: а = 2*m/√3. Осталось только этот результат умножить на 6. Получаем формулу периметра: p = 12*m/√3.
Дан радиус описанной окружности:
- Радиус описанной вокруг правильного шестиугольника окружности равен стороне этого шестиугольника.
Формула площади: S = (3√3*a²)/2
Дан радиус вписанной окружности:
- Формула площади: S = 3√3*r², где r = √3*a/2 (a – одна из сторон многоугольника).
Как найти площадь неправильного шестиугольника
Формулы для вычисления площади неправильного шестиугольника – многоугольника, стороны которого не равны между собой.
Метод трапеции:
- Делим шестиугольник на произвольные трапеции, вычисляем площадь каждой из них и складываем.
- Основные формулы площади трапеции: S = 1/2*(a + b)*h, где a и b – основания трапеции, h – высота.
S = h*m, где h – высота, m – средняя линия.
Известны координаты вершин шестиугольника:
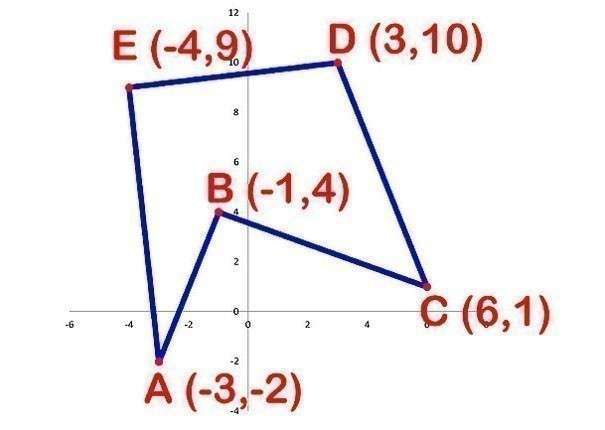
- Для начала запишем координаты точек, причём, располагая их не в хаотичном порядке, а последовательно друг за другом. Например:
A: (-3, -2)
B: (-1, 4)
C: (6, 1)
D: (3, 10)
E: (-4, 9)
F: (-5, 6) - Далее, внимательно, умножаем координату x каждой точки на координату y следующей точки:
-3*4 = -12
-1*1 = -1
6*10 = 60
3*9 = 27
-4*6 = -24
-5*(-2) = 10
Результаты складываем:
-12 – 1 + 60 + 27 – 24 + 10 = 60
Далее умножаем координату y каждой точки на координату x следующей точки.
-2*(-1) = 2
4*6 = 24
1*3 = 3
10*(-4) = -40
9*(-5) = -45
6*(-3) = -18
Результаты складываем:
2 + 24 + 3 – 40 – 45 – 18 = -74
Из первого результата вычитаем второй:
60 -(-74) = 60 + 74 = 134
Полученное число делим на два:
134/2 = 67
Ответ: 67 квадратных единиц.
- Также для нахождения площади шестиугольника вы можете разбить его на треугольники, квадраты, прямоугольники, параллелограммы и так далее. Найти площади составляющих его фигур и сложить.
Итак, методы нахождения площади шестиугольника на все случаи жизни изучены. Теперь вперёд, применять полученные знания! Удачи!
Математические свойства
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности ,
поскольку
Все углы равны 120°.
Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:
Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.
Шестиугольный паркет (шестиугольный паркетаж)
— замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — {6,3}, что означает, что в каждой вершине паркета сходятся три шестиугольника.
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна .
В 1940 году было доказано, что данная упаковка является самой плотной.
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной
(лемма Пала).
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Правильный шестиугольник в природе, технике и культуре
показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
Некоторые сложные кристаллы и молекулы
, например графит, имеют гексагональную кристаллическую решётку.
Образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
Памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.
Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
Сечение гайки
имеет вид правильного шестиугольника.
Конвертер единиц расстояния и длины Конвертер единиц площади Присоединяйтесь © 2011-2017 Довжик Михаил Копирование материалов запрещено. В онлайн калькуляте можно использовать величины в одинаквых единицах измерения! Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади. Дополнительные возможности калькулятора вычисления площади четырехугольника
- Между полями для ввода можно перемещаться нажимая клавиши «вправо» и «влево» на клавиатуре.
Теория. Площадь четырехугольника Четырёхугольник — геометрическая фигура, состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Четырёхугольник называется выпуклым, если отрезок соединяющий любые две точки этого четырехугольника, будет находиться внутри него.
Как узнать площадь многоугольника?
Формула определения площади определяется путем взятия каждого ребра многоугольника АВ, и вычисления площади треугольника АВО с вершиной в начале координат О, через координаты вершин. При обходе вокруг многоугольника, образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника.
Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется если она слева и вычитается если она справа с точки зрения из начала координат. Формула площади действительна для любого самонепересекающегося (простого) многоугольника, который может быть выпуклым или вогнутым. Содержание
- 1 Определение
- 2 Примеры
- 3 Более сложный пример
- 4 Объяснение названия
- 5 См.
Площадь многоугольника
Внимание
Это может быть:
- треугольник;
- четырехугольник;
- пяти- или шестиугольник и так далее.
Такая фигура непременно будет характеризоваться двумя положениями:
- Смежные стороны не принадлежат одной прямой.
- У несмежных отсутствуют общие точки, то есть они не пересекаются.
Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне. Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин.
Какие их виды существуют? Многоугольник, у которого больше четырех углов, может быть выпуклым или вогнутым. Отличие последнего в том, что некоторые его вершины могут лежать по разные стороны от прямой, проведенной через произвольную сторону многоугольника.
Как найти площадь правильного и неправильного шестиугольника?
- Зная длину стороны, умножим её на 6 и получим периметр шестиугольника:10 см х 6 = 60 см
- Подставим полученные результаты в нашу формулу:
Площадь = 1/2*периметр*апофему Площадь = ½*60см*5√3 Решаем: Теперь осталось упростить ответ, чтобы избавиться от квадратных корней, а полученный результат укажем в квадратных сантиметрах: ½ * 60 см * 5√3 см =30 * 5√3 см =150 √3 см =259.8 см² Видео о том, как найти площадь правильного шестиугольника Существует несколько вариантов определения площади неправильного шестиугольника:
- Метод трапеции.
- Метод расчета площади неправильных многоугольников при помощи оси координат.
- Метод разбивания шестиугольника на другие фигуры.
В зависимости от исходных данных, которые вам будут известны, подбирается подходящий метод.
Важно
Некоторые неправильные шестиугольники состоят из двух параллелограммов. Для определения площади параллелограмма следует умножить его длину на ширину и затем сложить две уже известные площади. Видео о том, как найти площадь многоугольника Равносторонний шестиугольник имеет шесть равных сторон и является правильным шестиугольником.
Площадь равностороннего шестиугольника равняется 6 площадям треугольников, на которые разбита правильная шестиугольная фигура. Все треугольники в шестиугольнике правильной формы равны, поэтому для нахождения площади такого шестиугольника достаточно будет знать площадь хотя бы одного треугольника. Для нахождения площади равностороннего шестиугольника используется, конечно же, формула площади правильного шестиугольника, описанная выше.
404 not found
Украшение жилища, одежды, рисование картин способствовало процессу формирования и накопления сведений в области геометрии, которые люди тех времён добывали опытным путем, по крупицам и передавали из поколения в поколение. Сегодня знания геометрии необходимы и закройщику, и строителю, и архитектору и каждому простому человеку в быту. Поэтому нужно учиться рассчитывать площадь различных фигур, и помнить, что каждая из формул может пригодиться впоследствии на практике, в том числе, и формула правильного шестиугольника.
Шестиугольником называется такая многоугольная фигура, общее количество углов которой равно шести. Правильным шестиугольником называют шестиугольную фигуру, которая имеет равные стороны. Углы у правильного шестиугольника также между собой равны.
В повседневной жизни мы часто можем встретить предметы, имеющие форму правильного шестиугольника.
Калькулятор площади неправильного многоугольника по сторонам
Вам понадобится
- — рулетка;
- — электронный дальномер;
- — лист бумаги и карандаш;
- — калькулятор.
Инструкция 1 Если вам нужна общая площадь квартиры или отдельной комнаты, просто прочтите технический паспорт на квартиру или дом, там указан метраж каждого помещения и общий метраж квартиры. 2 Для измерения площади прямоугольной или квадратной комнаты возьмите рулетку или электронный дальномер и измерьте длину стен. При измерении расстояний дальномером обязательно следите за перпендикулярностью направления луча, иначе результаты замеров могут быть искажены. 3 Затем полученную длину (в метрах) комнаты умножьте на ширину (в метрах). Полученное значение и будет площадью пола, она измеряется в квадратных метрах.
Формула площади гаусса
Если требуется посчитать площадь пола более сложной конструкции, например, пятиугольной комнаты или комнаты с круглой аркой, схематично начертите эскиз на листе бумаги. Затем разделите сложную форму на несколько простых, например, на квадрат и треугольник или прямоугольник и полукруг. Измерьте при помощи рулетки или дальномера величину всех сторон получившихся фигур (для круга необходимо узнать диаметр) и занесите результаты на ваш чертеж.
5 Теперь посчитайте площадь каждой фигуры по отдельности. Площадь прямоугольников и квадратов высчитывайте перемножением сторон. Для расчета площади круга диаметр разделите пополам и возведите в квадрат (умножьте его на самого себя), затем умножьте полученное значение на 3,14.
Если вам нужна только половина круга, разделите полученную площадь пополам. Чтобы рассчитать площадь треугольника, найдите Р, для этого сумму всех сторон поделите на 2.
Формула расчета площади неправильного многоугольника
Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, детерминанты будут отрицательными. Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина. Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости.
Для примера возьмём треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмём первую х -координату первой вершины и умножим её на y -координату второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определен по следующей формуле: A tri.
Формула расчета площади неправильного четырехугольника
A} _{text{tri.}}={1 over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}|} где xi и yi обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3. Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x5 и y5: A pent. = 1 2 | x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 5 + x 5 y 1 − x 2 y 1 − x 3 y 2 − x 4 y 3 − x 5 y 4 − x 1 y 5 | {displaystyle mathbf {A} _{text{pent.}}={1 over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{5}+x_{5}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{5}y_{4}-x_{1}y_{5}|} A для четырехугольника — переменные до x4 и y4: A quad.
С вопросом: «Как найти площадь шестиугольника?»
, можно столкнуться не только на экзамене по геометрии и т.п., эти знания пригодятся и в быту, например, для правильного и точного вычисления площади помещения в процессе ремонта. Подставив в формулу требуемые значения, получится определить нужное количество рулонов обоев, плитки в ванную или на кухню и т.д.
Немного фактов из истории
Геометрия использовалась еще в древнем Вавилоне
и прочих государствах, существовавших в одно время с ним. Вычисления помогали при возведении значительных сооружений, так как благодаря ей зодчие знали как выдержать вертикаль, правильно составить план, определить высоту.
Эстетика тоже имела большое значение, и здесь снова шла в ход геометрия. Сегодня этой науки нужны строителю, закройщику, архитектору, да и не специалисту тоже.
Поэтому лучше уметь рассчитывать S фигур, понимать, что формулы могут пригодиться на практике.
Площадь правильного 6-угольника
Итак, у нас шестиугольная фигура с равными сторонами и углами
. В повседневности мы часто имеем возможность встретить предметы правильной шестиугольной формы.
К примеру:
- гайка;
- пчелиные соты;
- снежинка.
Шестиугольная фигура наиболее экономично заполняет пространство на плоскости. Взгляните на тротуарную плитку, одна подогнана к другой так, что зазоров не остается.
Каждый угол равен 120˚. Сторона фигуры равна радиусу описанной окружности
.
Расчет
Требуемое значение можно вычислить, разбив фигуру на шесть треугольников с равными сторонами.
Вычислив S одного из треугольников, нетрудно определить и общую. Простая формула, так как правильный шестиугольник, по сути, является шестью равными треугольниками. Таким образом, для ее расчета найденную площадь одного треугольника умножают на 6.
Если от центра шестиугольника к любой его стороне провести перпендикуляр, получается отрезок – апофема
.
Посмотрим, как находить S шестиугольника, если апофема известна:
- S =1/2×периметр×апофема.
- Возьмем апофему равную 5√3 см.
- Находим периметр, используя апофему: так как апофема перпендикулярно к стороне 6-угольника, углы треугольника, образованного с помощью апофемы, равняются 30˚-60˚-90˚. Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза — 2x.
- Апофему x√3 можно подставить в формулу a=x√3. Если апофема равна 5√3, подставив данную величину, получим: 5√3см=x√3, или x=5см.
- Короткая сторона треугольника составляет 5см, так как эта величина – половина длины стороны 6-угольника. Умножив 5 на 2, получим 10см, что есть значение длиной стороны.
- Полученную величину умножим на 6 и получим значение периметра – 60см.
Подставляем полученные результаты в формулу: S=1/2×периметр×апофема
S=½×60 см× 5√3
Считаем:
Упрощаем полученный ответ, чтоб избавиться от корней. Результат будет выражен в квадратных сантиметрах: ½×60см×5√3см=30×5√3см=150 √3см=259,8с м².
Как находить площадь неправильного шестиугольника
Есть несколько вариантов:
- Разбивка 6-угольника на другие фигуры.
- Метод трапеции.
- Расчет S неправильных многоугольников с помощью осей координат.
Выбор способа диктуется исходными данными.
Метод трапеции
Шестиугольник делится на отдельные трапеции, после чего вычисляется площадь каждой полученной фигуры.
Использование осей координат
Используем координаты вершин многоугольника:
- В таблицу записываем координаты вершин x и y . Последовательно выбираем вершины, «двигаясь» против часовой стрелки, завершая список повторной записью координат первой вершины.
- Умножаем значения координаты x 1-й вершины на значение y 2-й вершины, и продолжаем так умножать. Складываем полученные результаты.
- Значения координат y1-й вершины умножаем на значения координат x 2-й вершины. Складываем результаты.
- Вычитаем сумму, полученную на 4-м этапе из суммы, полученной на третьем этапе.
- Делим результат, полученный на предыдущем этапе, и находим, что искали.
Разбивка шестиугольника на другие фигуры
Многоугольники разбиваются на другие фигуры: трапеции, треугольники, прямоугольники. Пользуясь формулами вычисления площадей перечисленных фигур, требуемые значения вычисляются и складываются.
Неправильный шестиугольник может состоять из двух параллелограммов. Чтоб вычислить площадь параллелограмма, его длина умножается на его ширину, а далее уже известные две площади складываются.
Площадь равностороннего шестиугольника
У правильного шестиугольника шесть равных сторон. Площадь равносторонней фигуры равна 6S треугольников, на которые разбит правильный шестиугольник. Каждый треугольник в правильном шестиугольнике равен, поэтому для вычисления площади такой фигуры довольно знать площадь хотя б одного треугольника.
Чтоб найти искомое значение пользуются формулой площади правильной фигуры, описанной выше.
Оглавление:
- Площадь правильного шестиугольника
- Площадь неправильного шестиугольника
- Площадь равностороннего шестиугольника
Умение определять площадь различных фигур играет немалую
роль в жизни каждого человека. Рано или поздно приходится иметь дело с этими
знаниями. К примеру, в процессе ремонта помещения для определения необходимого
количества рулонов обоев, линолеума, паркета, плитки в ванную или на кухню
нужно уметь рассчитывать необходимую площадь.
Знаниями в области геометрии пользовались еще в древнем
Вавилоне и других странах. На первых шагах к культуре всегда возникала
необходимость измерить участок, расстояние. При строительстве первых
значительных сооружений требовались умения выдерживать вертикаль,
спроектировать план.
Роль эстетических потребностей людей также имела немалое
значение. Украшение жилища, одежды, рисование картин способствовало процессу
формирования и накопления сведений в области геометрии, которые люди тех времён
добывали опытным путем, по крупицам и передавали из поколения в поколение.
Сегодня знания геометрии необходимы и закройщику, и строителю,
и архитектору и каждому простому человеку в быту.
Поэтому нужно учиться рассчитывать площадь различных
фигур, и помнить, что каждая из формул может пригодиться впоследствии на
практике, в том числе, и формула правильного шестиугольника. Шестиугольником называется
такая многоугольная фигура, общее количество углов которой равно шести.
Площадь правильного шестиугольника
Правильным шестиугольником называют шестиугольную фигуру,
которая имеет равные стороны. Углы у правильного шестиугольника также между
собой равны.
В повседневной жизни мы часто можем встретить предметы,
имеющие форму правильного шестиугольника. Это и металлическая гайка, и ячейки
пчелиных сот, и структура снежинки. Шестиугольными фигурами отлично заполняются
плоскости. Так, например, при мощении тротуарной плитки мы можем наблюдать, как
плитка укладывается одна возле другой, не оставляя пустых мест.
Свойства
правильного шестиугольника
- Правильный шестиугольник всегда будет иметь равные углы,
каждый из которых составляет 120˚. - Сторона фигуры равняется радиусу описанной окружности.
- Все стороны в правильном шестиугольнике равны.
- Правильный шестиугольник плотно заполняет плоскость.
Как посчитать
площадь правильного шестиугольника?
Площадь правильного шестиугольника можно рассчитать,
разбив его на шесть треугольников, каждый из которых будет иметь равные
стороны.
Для расчета площади правильного треугольника используется
следующая формула:
Зная площадь одного из треугольников, можно легко
рассчитать площадь шестиугольника. Формула для ее расчета проста: поскольку
правильный шестиугольник — это шесть равных треугольников, следует площадь
нашего треугольника умножить на 6.
Если провести от центра фигуры к любой из ее сторон
перпендикуляр, получим отрезок, который называется апофема. Рассмотрим, как
найти площадь шестиугольника при известной апофеме:
- Площадь = 1/2*периметр*апофему.
- Предположим, наша апофема равняется 5√3 см.
- Используя апофему, находим периметр: Поскольку апофема
расположена перпендикулярно к стороне шестиугольника, то углы треугольника,
созданного при помощи апофемы, будут равняться 30˚—60˚—90˚. Каждая сторона
полученного треугольника будет соответствовать: x-x√3-2x,
где короткая сторона, которая расположена напротив угла в 30˚— это x, длинная сторона,
расположенная напротив угла в 60˚ — это x√3,
а гипотенуза — 2x. - Поскольку апофема представлена, как x√3, можно подставить ее в формулу a = x√3 и решить. Если, к примеру,
апофема = 5√3, тогда подставим эту
величину в формулу и получим: 5√3 см = x√3, или x = 5
см. - Итак, короткая сторона треугольника равняется 5 см.
поскольку эта величина является половиной длины стороны шестиугольника,
умножаем 5 на 2 и получим 10 см, которая является длиной стороны. - Зная длину стороны, умножим её на 6 и получим периметр
шестиугольника:10 см х 6 = 60 см - Подставим полученные результаты в нашу формулу:
Площадь =
1/2*периметр*апофему
Площадь = ½*60см*5√3
Решаем:
Теперь осталось упростить
ответ, чтобы избавиться от квадратных корней, а полученный результат укажем в
квадратных сантиметрах:
½ * 60 см * 5√3 см =30 * 5√3
см =150 √3 см =259.8 см²
Видео о том, как найти площадь правильного шестиугольника
Площадь неправильного шестиугольника
Существует несколько вариантов определения площади
неправильного шестиугольника:
- Метод трапеции.
- Метод расчета площади неправильных многоугольников при
помощи оси координат. - Метод разбивания шестиугольника на другие фигуры.
В зависимости от исходных данных, которые вам будут
известны, подбирается подходящий метод.
Метод трапеции
Площадь шестиугольника, имеющего произвольную
(неправильную) форму, рассчитывается методом трапеции, суть которого состоит в
разделении шестиугольника на отдельные трапеции и последующим вычислением
площади каждой из них.
Метод с осями
координат
Кроме этого, площадь неправильного шестиугольника можно рассчитать
при помощи метода расчета площади неправильных многоугольников. Рассмотрим его
на следующем примере:
Вычисление будем выполнять методом использования
координат вершин многоугольника:
- На этом этапе следует сделать таблицу и записать
координаты вершин x и y. Выбираем вершины в
последовательном порядке по направлению против часовой стрелки, завершив конец
списка повторной записью координаты первой вершины:
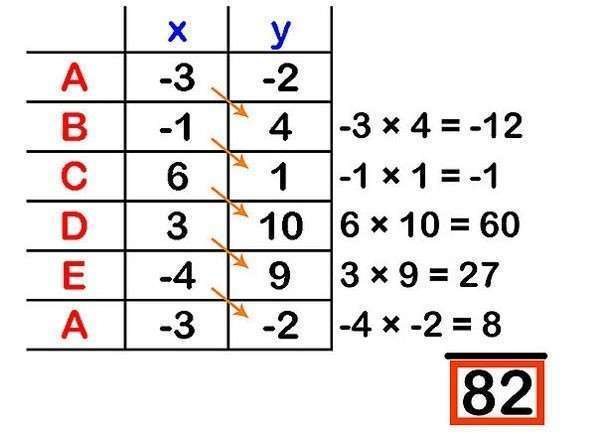
- Теперь следует умножить значения координаты х 1-й вершины
на y 2-й
вершины и продолжить таким образом умножение далее. Затем необходимо сложить
полученные результаты. В нашем случае получилось 82:
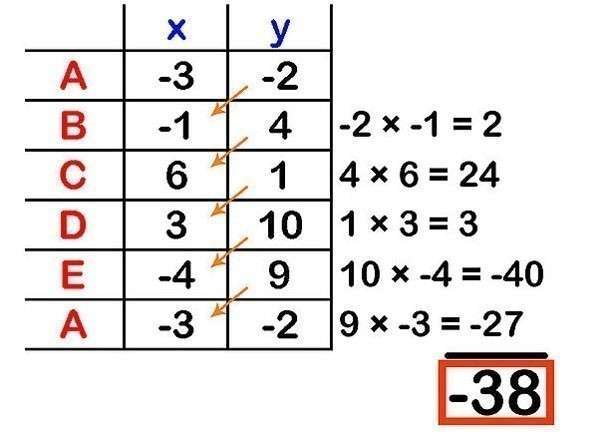
- Последовательно умножаем значения координат y1-й
вершины на значения координат х 2-й вершины. Суммируем полученные результаты. В
нашем случае получилось 38:
- Вычитаем сумму, которую получили на четвертом этапе из
суммы, которая получилась на третьем этапе: 82 – (-38) = 120
- Теперь необходимо разделить результат, который был
получен на предыдущем этапе и найдем площадь нашей фигуры: S= 120/2 = 60
см²
Метод разбивания
шестиугольника на другие фигуры
Каждый многоугольник можно разделить на несколько других
фигур. Это могут быть треугольники, трапеции, прямоугольники. Исходя из
известных данных, пользуясь формулами определения площадей перечисленных фигур,
последовательно вычисляются их площади и затем суммируются.
Некоторые неправильные шестиугольники состоят из двух
параллелограммов. Для определения площади параллелограмма следует умножить его
длину на ширину и затем сложить две уже известные площади.
Видео о том, как найти площадь многоугольника
Площадь равностороннего шестиугольника
Равносторонний шестиугольник имеет шесть равных сторон и
является правильным шестиугольником.
Площадь равностороннего шестиугольника равняется 6
площадям треугольников, на которые разбита правильная шестиугольная фигура.
Все треугольники в шестиугольнике правильной формы равны,
поэтому для нахождения площади такого шестиугольника достаточно будет знать
площадь хотя бы одного треугольника.
Для нахождения площади равностороннего шестиугольника
используется, конечно же, формула площади правильного шестиугольника, описанная
выше.
А Вы знали, как найти площадь шестиугольника? Как думаете, где эти знания пригодятся Вам в жизни? Поделитесь своим мнением в комментариях.
Загрузить PDF
Загрузить PDF
Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников. Есть несколько способов найти площадь шестиугольника, в зависимости от того, имеете ли вы дело с правильным или неправильным шестиугольником. Из этой статьи вы узнаете, как именно находить площадь этой фигуры.
-
1
Запишите формулу. Так как правильный шестиугольник состоит из 6 равносторонних треугольников, то формула образована из формулы нахождения площади равностороннего треугольника: Площадь = (3√3 s2)/ 2 где s — длина стороны правильного шестиугольника.[1]
-
2
Определите длину одной стороны. Если известна длина стороны, то просто запишите ее. В нашем случае длина стороны — 9 см. Если длина стороны неизвестна, но известен периметр или апофема (высота одного из шести равносторонних треугольников, перпендикулярная стороне), то можно найти и длину стороны. Вот, как это делается:
- Если известен периметр, то просто разделите его на 6 и получите длину стороны. Если, например, периметр — 54 см, то, разделив 54 на 6, мы получим 9 см, длину стороны.[2]
- Если известна только апофема, то длину стороны можно вычислить, подставив апофему в формулу a = x√3 и затем умножив ответ на 2. Это делается потому, что апофема представляет собой сторону x√3 образуемого ей треугольника с углами 30-60-90 градусов. Если, например, апофема — 10√3, то x — 10 и длина стороны будет равна 10 * 2 или 20.
- Если известен периметр, то просто разделите его на 6 и получите длину стороны. Если, например, периметр — 54 см, то, разделив 54 на 6, мы получим 9 см, длину стороны.[2]
-
3
Подставьте значение длины стороны в формулу. Просто подставляем 9 в изначальную формулу. Получаем: площадь = (3√3 x 92)/2
-
4
Упростите ответ. Решите уравнение и запишите ответ. Ответ должен быть указан в квадратных единицах, ведь мы имеем дело с площадью. Вот, как это делается:
- (3√3 x 92)/2 =
- (3√3 x 81)/2 =
- (243√3)/2 =
- 420.8/2 =
- 210.4 см2
Реклама
-
1
Запишите формулу. Площадь = 1/2 x периметр x апофему.[3]
-
2
Запишите апофему. Скажем, она равна 5√3 см.
-
3
Используйте апофему для нахождения периметра. Апофема перпендикулярна стороне шестиугольника и создает треугольник с углами 30-60-90. Стороны такого треугольника соответствуют пропорции x-x√3-2x, где сторона короткой стороны, лежащей напротив угла в 30 градусов, представлена x, длина длинной стороны, лежащей напротив угла в 60 градусов, представлена x√3, а гипотенуза представлена 2x.[4]
- Апофема — сторона, представленная x√3. Таким образом, подставляем апофему в формулу a = x√3 и решаем. Если, например, длина апофемы — 5√3, то подставляем это число в формулу и получаем 5√3 см = x√3, или x = 5 см.
- Решая через x, мы нашли длину короткой стороны треугольника — 5 см. Эта длина представляет собой половину длины стороны шестиугольника. Умножив 5 на 2, мы получаем 10 см, длину стороны.
- Подсчитав, что длина стороны равна 10, умножаем это число на 6 и получаем периметр шестиугольника. 10 см х 6 = 60 см.
-
4
Подставьте все известные данные в формулу. Сложнее всего найти периметр. Теперь надо лишь подставить апофему и периметр в формулу и решить:
- Площадь = 1/2 x периметр x апофему
- Площадь = 1/2 x 60 см x 5√3 см
-
5
Упрощайте ответ до тех пор, пока не избавитесь от квадратных корней. Окончательный ответ укажите в квадратных единицах.
- 1/2 x 60 см x 5√3 см =
- 30 x 5√3 см =
- 150√3 см =
- 259. 8 см2
Реклама
-
1
Запишите координаты всех вершин по осям x и y. Если известны вершины шестиугольника, то первым делом надо начертить таблицу с двумя колонками и семью рядами. Каждый ряд будет назван по названию по одной из шести точек (точка А, точка В, точка С и так далее), каждая колонка будет названа по осям x или у, соответствующим координатам точек по этим осям. Запишите координаты точки А по осям x и у справа от точки, координаты точки В — справа от точки В и так далее. Внизу повторно укажите координаты первой точки. Для примера скажем, что мы имеем дело со следующими точками, в формате (x, у):[5]
- A: (4, 10)
- B: (9, 7)
- C: (11, 2)
- D: (2, 2)
- E: (1, 5)
- F: (4, 7)
- A (снова): (4, 10)
-
2
Умножьте координаты каждой точки по оси x на координаты по оси у следующей точки. Это можно представить себе так: мы проводим диагональ вниз и вправо от каждой координаты по оси x. Запишем результаты справа от таблицы. Затем сложим их.
- 4 x 7 = 28
- 9 x 2 = 18
- 11 x 2 = 22
- 2 x 5 = 10
- 1 x 7 = 7
- 4 x 10 = 40
- 28 + 18 + 22 + 10 + 7 + 40 = 125
-
3
Умножьте координаты каждой точки по оси у на координаты по оси x следующей точки. Это можно представить себе так: мы проводим диагональ вниз и влево от каждой координаты по оси у. Перемножив все координаты, складываем результаты.
- 10 x 9 = 90
- 7 x 11 = 77
- 2 x 2 = 4
- 2 x 1 = 2
- 5 x 4 = 20
- 7 x 4 = 28
- 90 + 77 + 4 + 2 + 20 + 28 = 221
-
4
Вычтите из первой суммы координат вторую сумму координат. Вычитаем 221 из 125 и получаем -96. Итак, ответ: 96, площадь может быть только положительной.
-
5
Разделите разность на два. Делим 96 на 2 и получаем площадь неправильного шестиугольника. Окончательный ответ: 48 квадратных единиц.
Реклама
-
1
Найдите площадь правильного шестиугольника с отсутствующим треугольником. Если вы столкнулись с правильным шестиугольником, в котором отсутствует один или более треугольников, то прежде всего нужно найти его площадь, как если бы он был целым. Потом необходимо найти площадь «отсутствующего» треугольника и вычесть ее из общей площади. В итоге вы получите площадь имеющейся фигуры.[6]
- Например, если мы выяснили, что площадь правильного треугольника — 60 см2, а площадь отсутствующего треугольника — 10 см2, то: 60 см2 — 10 см2 = 50 см2.
- Если известно, что в шестиугольнике не хватает точно одного треугольника, то его площадь можно найти, умножив общую площадь на 5/6, так как мы имеем 5 и 6 треугольников. Если не хватает двух треугольников, то умножаем на 4/6 (2/3) и так далее.
-
2
Разбейте неправильный шестиугольник на треугольники. Найдите площади треугольников и сложите их. В зависимости от имеющихся данных существует множество способов найти площадь треугольника.[7]
-
3
Найдите в неправильном шестиугольнике какие-то другие фигуры: треугольники, прямоугольники, квадраты. Найдите площади составляющих шестиугольник фигур и сложите их.[8]
- Один из видов неправильного шестиугольника состоит из двух параллелограммов. Для нахождения их площадей просто перемножьте основания на высоты и затем сложите их площади.
Реклама
Об этой статье
Эту страницу просматривали 128 781 раз.
Была ли эта статья полезной?
Как рассчитать площадь правильного шестиугольника
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник — многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
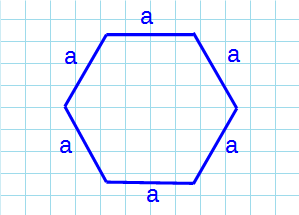
a:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через сторону:
a — сторона шестиугольника.
Через радиус описанной окружности
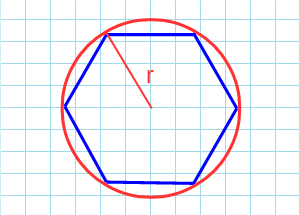
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
r — радиус описанной окружности.
Через радиус вписанной окружности
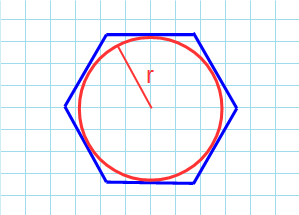
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности:
r — радиус вписанной окружности.