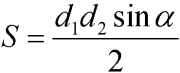Формулы площади
Все эти фигуры объединяет не только то, что они четырехугольные, но и то, что они еще и выпуклые. Достаточно просто рассмотреть схему:
Что такое четырех угольник
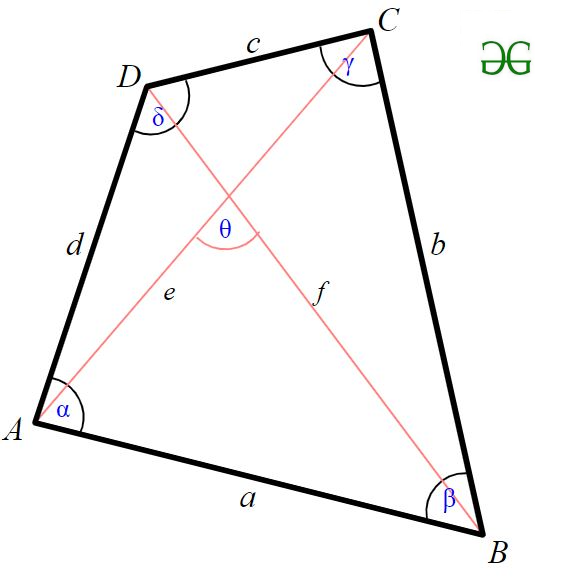
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки. Площадь четырехугольника равна полупроизведению его диагоналей и угла между ними.
Четырехугольник – это многоугольник с четырьмя вершинами, три из которых не лежат на одной прямой.
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, последовательно соединенная отрезками.
Формулы площади квадрата
Определения и соглашения
В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.
Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
- Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
- Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
- Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
- Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
- Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
- Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
- Угол между сторонами a и b будем обозначать следующей записью (a,b).
Площадь четырехугольника, заданного координатами
Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат. В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY .

Мы знаем, что все стороны фигуры равны, и формула площади квадрата находится по формуле:
Найдем одну из сторон, к примеру, AB :
Подставим значения в формулу:
Знаем, что все стороны одинаковые. Подставляем значение в формулу расчета площади:
Формула вычисления площади
Площадь (S) выпуклого четырехугольника равняется одной второй (половине) произведения его диагоналей и синуса угла между ними:
S = 1/2 * d1 * d2 * sin α
Нахождение площади четырёхугольника различными способами и методами
Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).
Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.
Теперь пусть даны стороны и противолежащие углы четырёхугольника.
Пусть a, b, c, d известные стороны многоугольника; p – его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).
На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.
Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.
Подставим полученные данные в нашу формулу, получим: S = rad((40 – 18)*(40 – 23)*(40 – 22)*(40 – 17) – 18*23*22*17*0,97) = rad(22*17*18*23 – 18*23*22*17*1/4) = rad((22*17*18*23*(1 – 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.
Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.
Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:
Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:
S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.
Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.
Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:
S = rad((65 – 26)*(65 – 35)*(65 – 39)*(65 – 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.
Особые виды четырехугольников
Четырехугольники могут обладать дополнительными свойствами, образуя особые виды геометрических фигур:
- Параллелограмм
- Ромб
- Прямоугольник
- Квадрат
- Трапеция
- Дельтоид
- Контрпараллелограмм
Квадрат, прямоугольник и другие параллелограммы
- Квадрат — это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
- Прямоугольник — это параллелограмм, у которого все стороны пересекаются под прямым углом.
- Ромб — это параллелограмм, у которого все стороны равны.
- ‘Площадь = длина х высота, или S = a х h.
- Пример: если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь этого прямоугольника: S = 10 х 5 = 50 квадратных сантиметров.
- Не забывайте, что площадь измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и так далее).
- Площадь = сторона х сторона, или S = a 2.
- Пример: если сторона квадрата равна 4 см (a = 4), то площадь этого квадрата: S = a 2 = 4 х 4 = 16 квадратных сантиметров.
- Площадь = (диагональ1 х диагональ2)/2, или S = (d1 × d2)/2
- Пример: если диагонали ромба равны 6 см и 8 см, то площадь этого ромба: S = (6 х 8)/2 = 24 квадратных сантиметров.
- Пример: если длина ромба равна 10 см, а его высота равна 3 см, то площадь такого ромба равна 10 х 3 = 30 квадратных сантиметров.
- Площадь = сторона х высоту, или S = a × h
- Площадь = (диагональ1 × диагональ2)/2, или S = (d1 × d2)/2
- Пример: если сторона квадрата равна 4 см, то его площадь равна 4 х 4 = 16 квадратных сантиметров.
- Пример: диагонали квадрата равны по 10 см. Вы можете найти площадь этого квадрата по формуле: (10 х 10)/2 = 100/2 = 50 квадратных сантиметров.
Пример задачи
Найдите площадь выпуклого четырехугольника, если его диагонали равны 5 и 9 см, а угол между ними составляет 30°.
Решение:
Подставляем в формулу известные нам значения и получаем: S = 1/2 * 5 см * 9 см * sin 30° = 11,25 см 2 .
Свойство диагоналей выпуклого четырехугольника
Диагонали выпуклого четырехугольника пересекаются. Действительно, это явление можно наблюдать визуально, достаточно взглянуть на рисунок:
На рисунке слева изображен невыпуклый четырехугольник или четырехсторонник. Как угодно. Как видно, диагонали не пересекаются, по крайней мере, не все. Справа изображен выпуклый четырехугольник. Тут уже наблюдается свойство диагоналей пересекаться. Это же свойство можно считать признаком выпуклости четырехугольника.
Свойства длин сторон четырехугольника
Модуль разности любых двух сторон четырёхугольника не превосходит суммы двух других его сторон.
Важно. Неравенство верно для любой комбинации сторон четырехугольника. Рисунок приведен исключительно для облегчения восприятия.
В любом четырёхугольнике сумма длин трёх его сторон не меньше длины четвёртой стороны.
Важно. При решении задач в пределах школьной программы можно использовать строгое неравенство (<). Равенство достигается только в случае, если четырехугольник является “вырожденным”, то есть три его точки лежат на одной прямой. То есть эта ситуация не попадает под классическое определение четырехугольника.
Площадь четырехугольника по сторонам
Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d формула полупериметра будет выглядеть так:
Зная стороны, выводим формулу. Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны:

используем найденное значение для расчета площади:
Четырехугольник и окружность
Четырехугольник, описанный вокруг окружности (окружность, вписанная в четырехугольник).
Главное свойство описанного четырехугольника:
Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин противоположных сторон равны.
Четырехугольник, вписанный в окружность (окружность, описанная вокруг четырехугольника)
Главное свойство вписанного четырехугольника:
Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны 180 градусов.
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
где d1 и d2 – диагонали четырёхугольника , а φ – любой из четырёх углов между ними (рис. 1).
Площади четырехугольников
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
a и b – смежные стороны
d – диагональ,
φ – любой из четырёх углов между диагоналями
Получается из верхней формулы подстановкой d=2R
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
a – сторона,
ha – высота, опущенная на эту сторону
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
a – сторона,
ha – высота, опущенная на эту сторону
a – сторона,
φ – любой из четырёх углов ромба
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
a и b – основания,
c и d – боковые стороны
a и b – неравные стороны,
φ – угол между ними
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,
Формулу называют «Формула Брахмагупты»
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
где
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
где
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
| Прямоугольник |
 |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
где
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны ,
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
где
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле
где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Площадь четырехугольника
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Площадь четырехугольника по диагоналям и углу между ними
Площадь четырехугольника через стороны и углы между этими сторонами
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади четырехугольника
Площадь частных случаев четырехугольников
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
Как найти площадь четырехугольника?
Если на плоскости поочередно начертить несколько отрезков так, чтоб каждый последующий начинался в том месте, где завершился предшествующий, то получится ломаная линия. Эти отрезки именуют звеньями, а места их скрещения — верхушками. Когда конец последнего отрезка пересечется с исходной точкой первого, то получится замкнутая ломаная линия, делящая плоскость на две части. Одна из их является конечной, а 2-ая нескончаемой.
Обычная замкнутая линия вкупе с заключенной в ней частью плоскости (той, которая конечна) именуют многоугольником. Отрезки являются сторонами, а образованные ими углы — верхушками. Количество сторон хоть какого многоугольника равно числу его вершин. Фигура, которая имеет три стороны, именуется треугольником, а четыре — четырехугольником. Многоугольник численно характеризуется таковой величиной, как площадь, которая указывает размер фигуры. Как отыскать площадь четырехугольника? Этому учит раздел арифметики — геометрия.
Чтоб отыскать площадь четырехугольника, необходимо знать к какому типу он относится — выпуклому либо невыпуклому? Выпуклый многоугольник весь лежит относительно прямой (а она непременно содержит какую-либо из его сторон) по одну сторону. Не считая того, есть и такие виды четырехугольников, как параллелограмм с попарно равными и параллельными обратными сторонами (разновидности его: прямоугольник с прямыми углами, ромб с равными сторонами, квадрат со всеми прямыми углами и 4-мя равными сторонами), трапеция с 2-мя параллельными обратными сторонами и дельтоид с 2-мя парами смежных сторон, которые равны.
Площади хоть какого многоугольника находят, применяя общий способ, который состоит в том, чтоб разбить его на треугольники, для каждого вычислить площадь случайного треугольника и сложить приобретенные результаты. Хоть какой выпуклый четырехугольник делится на два треугольника, невыпуклый — на два либо три треугольника, площадь его в данном случае может складываться из суммы и разности результатов. Площадь хоть какого треугольника вычисляют как половину произведения основания (a) на высоту (h), проведенную к основанию. Формула, которая применяется в данном случае для вычисления, записывается как: S = ½ • a • h.
Как отыскать площадь четырехугольника, к примеру, параллелограмма? Необходимо знать длину основания (a), длину боковой стороны (b) и отыскать синус угла α, образованного основанием и боковой стороной (sinα), формула для расчета будет смотреться: S = a • b • sinα. Потому что синус угла α есть произведение основания параллелограмма на его высоту (h = b) — линию перпендикулярная основанию, то его площадь вычисляют, умножив на высоту его основание: S = a • h. Для расчета площади ромба и прямоугольника также подходит эта формула. Потому что у прямоугольника боковая сторона b совпадает с высотой h, то его площадь вычисляют по формуле S = a • b. Площадь квадрата, так как a = b, будет приравниваться квадрату его стороны: S = a • a = a². Площадь трапеции рассчитывается как половина суммы его сторон, умноженная на высоту (она проводится к основанию трапеции перпендикулярно): S = ½ • (a + b) • h.
Как отыскать площадь четырехугольника, если неопознаны длины его сторон, но известны его диагонали (e) и (f), также синус угла α? В этом случай площадь вычисляют, как половину произведения его диагоналей (полосы, которые соединяют верхушки многоугольника), умноженное на синус угла α. Формула может быть записана в таком виде: S = ½ • (e • f) • sinα. А именно площадь ромба в данном случае будет приравниваться половине произведения диагоналей (полосы, соединяющие обратные углы ромба): S = ½ • (e • f).
Как отыскать площадь четырехугольника, который не является параллелограммом либо трапецией, его обычно принято именовать случайный четырехугольник. Площадь таковой фигуры выражают через его полупериметр (Ρ — сумма 2-ух сторон с общей верхушкой), стороны a, b, c, d и сумму 2-ух обратных углов (α + β): S = √[( Ρ – a) • (Ρ – b) • (Ρ – c) • (Ρ – d) – a • b • c • d • cos² ½ (α + β)].
Если четырехугольник вписан в окружность, а φ = 180о, то для расчета его площади употребляют формулу Брахмагупты (индийский астролог и математик, живший в 6—7 веках нашей эпохи): S = √[( Ρ – a) • (Ρ – b) • (Ρ – c) • (Ρ – d)]. Если четырехугольник описан окружностью, то (a + c = b + d), а его площадь вычисляют: S = √[ a • b • c • d] • sin ½ (α + β). Если четырехугольник сразу является описанным одной окружностью и вписанным в другую окружность, то для вычисления площади употребляют последующую формулу: S = √[a • b • c • d].
Найдите площадь четырехугольника, вершины которого имеют координаты (4; 2), (8; 4), (6; 8), (2; 6).
Эту задачу можно назвать разновидностью задачи р площади фигуры в клетках. А клетки можно представить себе или даже нарисовать. Дорисуем фигуру в клетках до квадрата сторонами 8 на 8. Дальше решение стандартное: находим общую площадь (8*8 = 64), разбиваем незакрашенную часть на прямоугольные треугольники и прямоугольник, вычисляем площади и вычитаем и общей площади.
Итак, вокруг закрашенной фигуры выделяем 4 равных прямоугольных треугольника с катетами 2 и 4 и два прямоугольника (большой со сторонами 2 и 8 и маленький 2 и 6). Площади треугольников 2*4/2=4, площади прямоугольников 2*8=16 и 2*6=12, их суммарная площадь 4*4+16+12 = 44. Вычитаем из 64 эту сумму и получим ответ: 20. Конечно есть и другие способы решения, но данный метод достаточно универсальный (годится и для параллелограммов, и для трапеций), да и запомнить надо только одтн метод, так как задачи в клетках все равно будут.
система выбрала этот ответ лучшим
Master-Margarita
[135K]
3 года назад
Можно вычислить площадь большого квадрата, в который вписан наш искомый квадрат.
Сторона этого квадрата составляет 6 см (8-2=6).
Площадь квадрата вычисляется по формуле:
Отсюда, площадь большого квадрата: S=6*6=36 кв.см.
Из нее надо вычесть площадь квадрата со стороной 4 см. Так как из четырех треугольников можно сложить один квадрат. S=4*4=16.
Теперь осталось лишь найти разницу: 36-16=20 кв.см.
Ответ: 20 кв.см.
Vasil Stryzhak
[11.5K]
3 года назад
Площадь можно вычислить по формуле Пика для многоугольника с целочисленными вершинами.
S = a + b/2 – 1 = 4 +4/2 – 1 = 5,
где а — количество точек внутри многоугольника (красных), а b — количество точек на границе многоугольника (синих). Так как площадь клетки в 4 раза больше единичной, то площадь четырехугольника
5*4 = 20.
В качестве другого варианта, воспользуемся «формулой шнурков» (Гаусса). Построим матрицу из чисел координат. Соединим числа косыми отрезками.
S = (4*4 + 8*8 + 6*6 + 2*2 – 8*2 – 6*4 – 2*8 – 4*6)/2 = 20.
Никольский
[12.8K]
более года назад
Закрашенная фигура состоит из четырех прямоугольных треугольников с катетами 4 и 2
и квадрата со стороной 2.
Находим площади этих фигур.
Сумма площадей прямоугольных треугольников:
4 * ((4 * 2)/2) = 16
Площадь квадрата:
2 * 2 = 4
Площадь закрашенной фигуры: 16 + 4 = 20.
Евгений трохов
[56.5K]
3 года назад
По координатам точек можно найти что каждая сторона четырехугольника равна корень из 20.Значит фигура по крайней мере ромб.
Но на самом деле это квадрат.
Это тоже можно при желании доказать.
Площадь квадрата равна :
20^(1/2) *20^(1/2)=20
Ответ-20
helpau
[3.4K]
3 года назад
1)Разбить на два треугольника,далее применить либо теорему синусов/косинусов,либо формулу Герона.
2)Формула площади Гаусса.
3)Какие-либо соображения из курса аналитической геометрии(в частности,площадь треугольника через определитель матрицы).
Знаете ответ?
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given four sides of quadrilateral a, b, c, d, find the maximum area of the quadrilateral possible from the given sides .
Examples:
Input : 1 2 1 2 Output : 2.00 It is optimal to construct a rectangle for maximum area .
According to Bretschneider’s formula, the area of a general quadrilateral is given by
Here a, b, c, d are the sides of a quadrilateral, s is the semiperimeter of a quadrilateral and angles are two opposite angles.
So, this formula is maximized only when opposite angles sum to pi(180) then we can use a simplified form of Bretschneider’s formula to get the (maximum) area K.
This formula is called as Brahmagupta’s formula .
Below is the implementation of given approach
C++
#include <iostream>
#include <math.h>
using namespace std;
double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
int main()
{
double a = 1, b = 2, c= 1, d = 2;
cout <<maxArea(a, b, c, d);
return 0;
}
C
#include <stdio.h>
#include <math.h>
double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
int main()
{
double a = 1, b = 2, c= 1, d = 2;
printf("%.2fn",maxArea(a, b, c, d));
return 0;
}
Java
import java.io.*;
class GFG
{
static double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return Math.sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
public static void main (String[] args)
{
double a = 1, b = 2, c= 1, d = 2;
System.out.println(maxArea(a, b, c, d));
}
}
Python3
import math
def maxArea (a , b , c , d ):
semiperimeter = (a + b + c + d) / 2
return math.sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d))
a = 1
b = 2
c = 1
d = 2
print("%.2f"%maxArea(a, b, c, d))
C#
using System;
class GFG {
static double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return Math.Sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
public static void Main ()
{
double a = 1, b = 2, c= 1, d = 2;
Console.WriteLine(maxArea(a, b, c, d));
}
}
PHP
<?php
function maxArea( $a, $b, $c, $d)
{
$semiperimeter = ($a + $b + $c + $d) / 2;
return sqrt(($semiperimeter - $a) *
($semiperimeter - $b) *
($semiperimeter - $c) *
($semiperimeter - $d));
}
$a = 1; $b = 2; $c= 1; $d = 2;
echo(maxArea($a, $b, $c, $d));
?>
Javascript
<script>
function maxArea(a, b, c, d)
{
let semiperimeter = (a + b + c + d) / 2;
return Math.sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
let a = 1, b = 2, c= 1, d = 2;
document.write(maxArea(a, b, c, d));
</script>
Output:
2.00
Time Complexity: O(logn)
Auxiliary Space: O(1)
Please suggest if someone has a better solution which is more efficient in terms of space and time.
This article is contributed by Aarti_Rathi. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
Last Updated :
22 Jun, 2022
Like Article
Save Article
С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».
Как найти площадь неправильного четырехугольника?
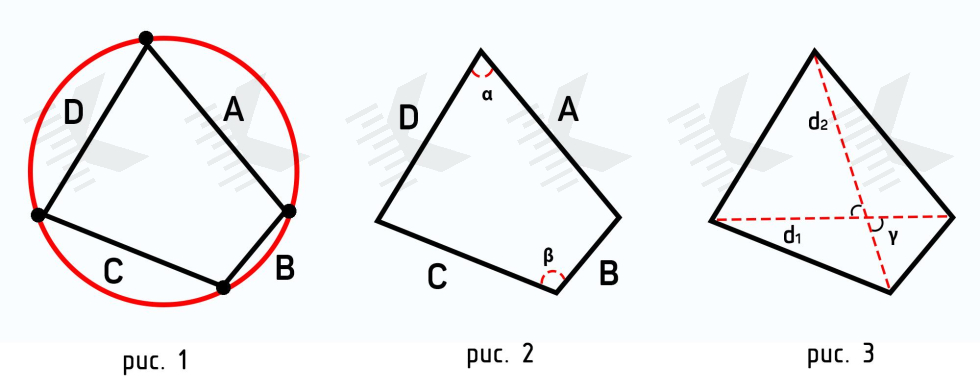
Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.
где P — полупериметр, a, b, c, d — длины сторон четырехугольника.
Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.
где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.
В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.
Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.
где d1, d2 — диагонали четырехугольника, α — острый угол между диагоналями.



 Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.