Как найти площадь трапеции abcd егэ

Трапеция и ее свойства

Т. А. Унегова

Определения:

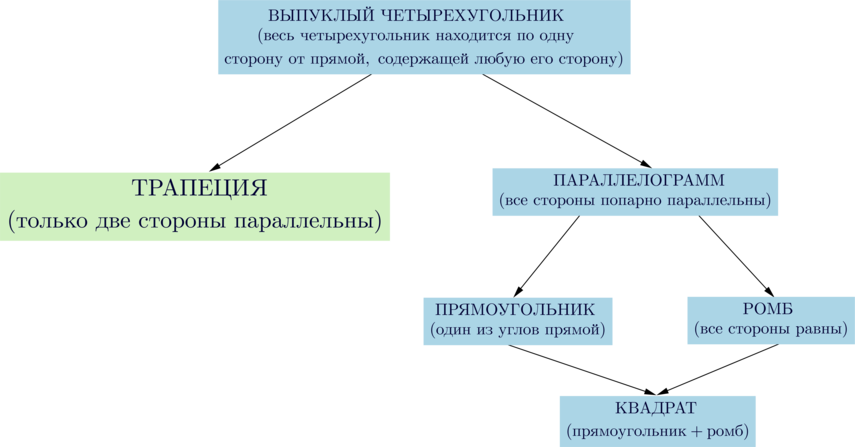
Трапеция — это называется четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.

Параллельные стороны называются основаниями трапеции, а непараллельные — боковыми сторонами трапеции.

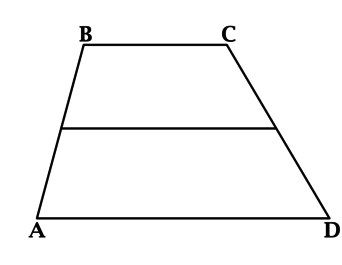
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

Если боковые стороны равны, трапеция называется равнобедренной.

Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание.

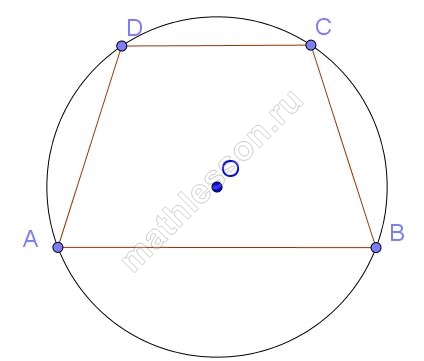
Трапеция называется вписанной в окружность, если каждая ее вершина принадлежит окружности.

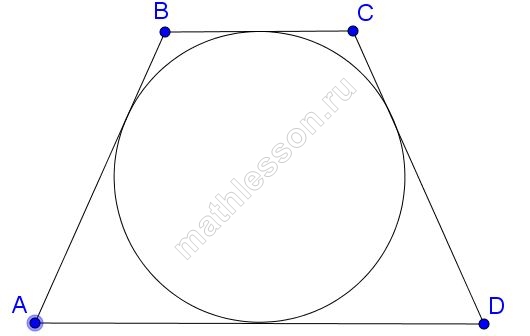
Трапеция называется описанной вокруг окружности, если каждая ее сторона касается окружности.

Трапеция называется равнобедренной (равнобокой, равнобочной), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Теоремы о средней линии и диагоналях трапеции

Теорема 1. Средняя линия трапеции параллельна основаниям и равна их полусумме: m=displaystyle frac{a+b}{2}.

Теорема 2. Диагонали трапеции делят среднюю линию трапеции на три отрезка. Средний из них равен полуразности оснований, а два крайних равны между собой: EF=GH, ; FG=displaystyle frac{a-b}{2}.

Теорема 3. Средняя линия треугольника, составленного из диагоналей и суммы оснований трапеции, равна средней линии трапеции: PQ=MN.

Теорема 4. Четыре точки: середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон — лежат на одной прямой.

Эта теорема называется также «Замечательное свойство трапеции».

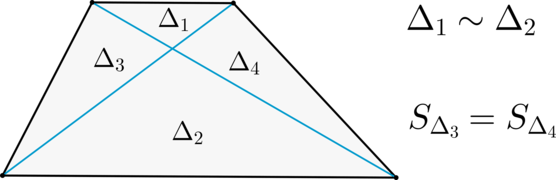
Теорема 5. Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.

Теоремы о площади трапеции

Теорема 6. Площадь трапеции равна произведению полусуммы ее оснований на высоту: S=displaystyle frac{a+b}{2}cdot h.

Теорема 7. Площадь трапеции равна произведению ее средней линии на высоту: S=mh.

Теорема 8. Площадь трапеции (как и всякого выпуклого четырехугольника) равна половине произведения ее диагоналей на синус угла между ними: S=displaystyle frac{1}{2}d_1d_2{sin alpha }, где d_1=AC, d_2=BD, alpha =angle BOA. (Вместо angle BOA можно брать angle BOC.)

Теорема 9. Если в трапецию можно вписать окружность, то (как и для всякого описанного многоугольника) площадь трапеции равна произведению ее полупериметра на радиус вписанной окружности: S=pr. Таким образом, S=displaystyle frac{a+b+c+d}{2}cdot r.

Теорема 10. Площадь трапеции равна площади треугольника, составленного из диагоналей и суммы оснований этой трапеции. (Сравни эту теорему и теорему 3.)

Теоремы о вписанных и описанных трапециях

Теорема 11. Если трапеция вписана в окружность, то она равнобедренная. И наоборот, если трапеция равнобедренная, то около нее можно описать окружность.

Теорема 12. Если трапеция описана около окружности, то сумма оснований трапеции равна сумме ее боковых сторон.

Задачи ЕГЭ и ОГЭ по теме: Трапеция

Задача 1.

Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны sqrt{2}.

Решение:

Высота трапеции— это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины B. Так как сторона квадратной клетки равна sqrt{2} , то по теореме Пифагора получаем, что h=2.

Ответ: 2.

Задача 2.

Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол {150}^{{}^circ }. Найдите площадь трапеции.

Решение:

Углы angle ABC и angle BAH — односторонние, их сумма равна {180}^{{}^circ }, и тогда angle BAH =30{}^circ .

Из vartriangle ABH найдем высоту BH. Катет, лежащий против угла в {30}^{{}^circ }, равен половине гипотенузы. Получаем, что BH = 3,5.

Площадь трапеции равна S=displaystyle frac{6+18}{2}cdot 3,5=42.

Ответ: 42.

Задача 3.

Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ.

Решение:

Что можно увидеть на чертеже? Можно сказать, что изображена трапеция ABCD, и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, ABC и ACD, в которых проведены средние линии.

Напомним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны. Из vartriangle ACD находим, что x=5.

Ответ: 5.

Задача 4.

Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Решение:

Проведем PQ — среднюю линию трапеции, PQ = 2,5 и PQparallel BC. Отсюда получаем, что M- середина отрезка AC, то есть PM — средняя линия треугольника ABC и PM = 1. Аналогично, NQ = 1.

x=MN=PQ-PM-NQ=0,5.

Ответ: 0,5.

Задача 5.

Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Решение:

Периметр треугольника равен сумме его сторон, то есть a+b+c=15.

Периметр трапеции равен

a+b+4+c+4=left(a+b+cright)+8=15+8=23.

Ответ: 23.

Задача 6.

В равнобедренной трапеции ABCD диагональ AC является биссектрисой острого угла трапеции и образует со стороной CD угол 63{}^circ . Найдите углы трапеции.

Решение:

Пусть angle CAD =alpha , тогда angle CAB =alpha и angle BAD =2alpha , так как трапеция равнобедренная.

Сумма углов vartriangle ACD=3alpha +63{}^circ =180{}^circ , откуда
alpha =39{}^circ .
Итак, angle D=78{}^circ , аangle BCD=180{}^circ -78{}^circ =102{}^circ .

Ответ: 78{}^circ , 102{}^circ .

Задача 7.

В равнобедренной трапеции основания равны 10 м и 24 м, боковая сторона 25 м. Найдите высоту трапеции.

Решение:

В равнобедренной трапеции проведем высоты. Получим прямоугольник и два равных прямоугольных треугольника. Тогда основание каждого треугольника равно 7 и h^2={25}^2-7^2=left(25-7right)left(25+7right)=18cdot 32. Отсюда, h=sqrt{18cdot 32}=sqrt{9cdot 64}=3cdot 8=24.

Ответ: 24.

Задача 8.

Тупой угол равнобедренной трапеции равен {135}^circ , а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.

Решение:

Проведем две высоты. Они разделят трапецию на три части: прямоугольник и два равных прямоугольных треугольника с острым углом 45{}^circ .

Каждый треугольник равнобедренный, поэтому h = 1,4.

Нетрудно видеть, что верхнее основание трапеции равно 2, а нижнее — 4,8. Отсюда площадь трапеции равна displaystyle frac{2+4,8}{2}cdot 1,4=4,76.

Ответ: 4,76.

Задача 9.

Площадь трапеции равна 60м^2, а основания 8 м и 12 м. Найдите высоту трапеции.

Решение:

Так как площадь трапеции S=displaystyle frac{a+b}{2}cdot h, то 60=displaystyle frac{8+12}{2}cdot h, откуда h = 6.

Ответ: 6.

Задача 10.

В равнобедренной трапеции диагонали перпендикулярны и равны a. Найдите площадь трапеции.

Решение:

Проведем CE parallel BD и DE — продолжение AD.

Так как BCDE — параллелограмм, то CE = a.

По теореме 10 получим, что S_{ABCD}=S_{ACE}=displaystyle frac{1}{2}a^2.

Ответ: displaystyle frac{1}{2}a^2

Задач 11.

В трапеции ABCD с большим основанием AD диагональ AC перпендикулярна к боковой стороне CD и является биссектрисой угла A.

Найдите AD, если периметр трапеции равен 20, а угол D равен 60{}^circ .

Решение:

По условию задачи в прямоугольном vartriangle ACD

angle D =60{}^circ , следовательно, angle CAD =30{}^circ .

Так как AC — биссектриса, то angle CAB =30{}^circ , откуда angle DAB =60{}^circ , то есть, трапеция равнобедренная. angle BCA =angle CAD =30{}^circ как накрест лежащие, поэтому vartriangle ABC — равнобедренный.

Обозначим длины боковых сторон vartriangle ABC буквой x.

Тогда AB = BC = CD = x, и AD = 2x, так как в прямоугольном vartriangle ACD против угла в 30{}^circ лежит катет, равный половине гипотенузы.

Таким образом, периметр трапеции, равный 20, составляет 5x, отсюда

x = 4 и AD = 8.

Ответ: 8.

Задача 12.

В равнобедренной трапеции ABCD с острым углом 60{}^circ меньшее основание BC равно 2, а боковая сторона AB равна 10. Продолжения боковых сторон трапеции пересекаются в точке M. Во сколько раз площадь трапеции больше площади треугольника BCM?

Решение:

Нетрудно видеть, что vartriangle BCM равносторонний и BM = 2, тогда AM = 12 и vartriangle BCM подобен vartriangle ADM c коэффициентом k=12:2=6.

Пусть S_{BCM}=S_1, S_{ADM}=S_2, тогда

S_2=k^2cdot S_1=36{cdot S}_1.

Площадь трапеции будет равна

S_{ABCD}=S_2-S_1=36 S_1-S_1=35 S_1=35 S_{BCM}.

Ответ: 35.

Задача 13.

Сумма углов при одном из оснований трапеции равна 90{}^circ . Найдите длину отрезка, соединяющего середины оснований, если основания равны 6 и 10.

Решение:

Продолжим боковые стороны до пересечения в точке E и отметим точки F и G — середины оснований трапеции.

Так как сумма углов при основании трапеции равна 90{}^circ , то angle BEC=90{}^circ , поэтому EF и EG — медианы в прямоугольных треугольниках BEC и AED соответственно.

Известно, что медиана, проведенная к гипотенузе, равна ее половине, значит FG=EG-EF=AG-BF=5-3=2.

Ответ: 2.

Задача 14.

Найдите радиус окружности, вписанной в равнобочную трапецию, если средняя линия трапеции равна 10, а ее площадь 24.

Решение:

Так как площадь трапеции равна S=mh, а высота трапеции равна диаметру вписанной окружности, то есть h=2r, то 24=10cdot 2r, откуда r=1,2.

Ответ: 1,2.

Задача 15.

Периметр прямоугольной трапеции равен 32, а большая боковая сторона равна 10. Найдите радиус r вписанной в трапецию окружности.

Решение:

По свойствам описанной трапеции сумма ее боковых сторон равна сумме оснований, поэтому

AB+CD=32:2=16, откуда AB=16-10=6.

Сторона AB равна диаметру окружности, поэтому r=3.

Ответ: 3.

Задача 16.

Около окружности описана трапеция, сумма боковых сторон которой равна 40. Найдите длину ее средней линии.

Решение:

Длина средней линии трапеции равна полусумме оснований. Если трапеция описана вокруг окружности, то в ней сумма оснований равна сумме боковых сторон, поэтому

m=displaystyle frac{a+b}{2}=displaystyle frac{c+d}{2}=displaystyle frac{40}{2}=20.

Ответ: 20.

Задача 17.

В окружность вписана трапеция так, что диаметр окружности служит основанием трапеции, а вершины другого основания делят полуокружность на три равные части. Найдите тупые углы трапеции. Ответ выразите в градусах.

Решение:

Так как AD — диаметр окружности, то дуга ABCD равна 180{}^circ . Она делится на три равные части по 60{}^circ .

Вписанный угол D опирается на дугу ABC, которая равна 120{}^circ , отсюда angle ADC=60{}^circ и, стало быть, angle C=120{}^circ =angle B.

Ответ: 120.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Трапеция и ее свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

3. Геометрия на плоскости (планиметрия). Часть I


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Произвольная трапеция

Сумма внутренних углов любого четырехугольника равна (360^circ).

Свойства трапеции:

(blacktriangleright) Сумма углов при боковой стороне равна (180^circ).

(blacktriangleright) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.

(blacktriangleright) Средняя линия трапеции – отрезок, соединяющий середины боковых сторон. Средняя линия параллельна основаниям и равна их полусумме.

Площадь трапеции

Площадь трапеции равна произведению полусуммы оснований на высоту.


Задание
1

#3091

Уровень задания: Равен ЕГЭ

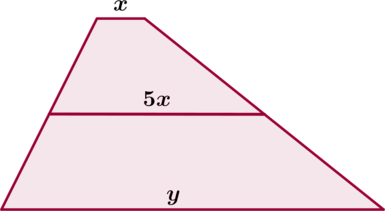
Одно из оснований трапеции в (5) раз меньше ее средней линии. Во сколько раз оно меньше другого основания трапеции?

Обозначим меньшее основание трапеции за (x), большее – за (y). Тогда (5x) – длина средней линии трапеции. Так как средняя линия равна полусумме оснований, то [x+y=2cdot 5xquadLeftrightarrowquad y=9x.] Следовательно, меньшее основание в 9 раз меньше большего.

Ответ: 9


Задание
2

#1694

Уровень задания: Равен ЕГЭ

В трапеции (ABCD): (CD = BC), (angle BCD = 140^circ), (angle ABD = 100^circ). Найдите модуль разности острых углов трапеции.

(triangle BCD) – равнобедренный (Rightarrow) (angle CBD = angle CDB = 20^circ); (angle BAD = 180^circ — angle ABD — angle CBD = 180^circ — 100^circ — 20^circ = 60^circ); (angle ADC = 180^circ — 140^circ = 40^circ). Тогда (|angle ADC — angle BAD| = |40^circ — 60^circ| = |-20^circ| = 20^circ).

Ответ: 20


Задание
3

#290

Уровень задания: Равен ЕГЭ

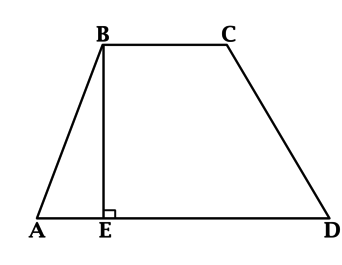
В трапеции (ABCD) с основаниями (BC = 5) и (AD = 2cdot BC) проведена высота (BE). Найдите отношение площади трапеции к длине этой высоты.

Площадь трапеции равна произведению полусуммы оснований на высоту. Полусумма оснований трапеции (ABCD) равна (0,5(5 + 2cdot 5) = 7,5). Площадь трапеции (ABCD) равна (7,5 BE), тогда (dfrac{S_{ABCD}}{BE} = 7,5).

Ответ: 7,5


Задание
4

#292

Уровень задания: Равен ЕГЭ

В трапеции (ABCD) с основаниями (BC = 4) и (AD > BC) угол (A) – прямой. Известно, что (CD = 6), (angle D = 60^{circ}). Найдите среднюю линию трапеции (ABCD).

Из точки (C) опустим высоту (CE). В прямоугольном треугольнике (CDE): (angle ECD = 30^{circ}). В прямоугольном треугольнике катет, лежащий против угла в (30^{circ}) равен половине гипотенузы, тогда (DE = 0,5cdot CD = 3). При этом (ABCE) – прямоугольник, (AE = BC = 4), тогда (AD = AE + ED = 4 + 3 = 7).

В трапеции средняя линия равна полусумме оснований. (0,5(BC + AD) = 0,5(4 + 7) = 5,5), значит, длина средней линии равна (5,5).

Ответ: 5,5


Задание
5

#293

Уровень задания: Равен ЕГЭ

В трапеции (ABCD) средняя линия составляет (dfrac{4}{5}) одного из оснований. Найдите отношение длины другого основания к длине средней линии.

Средняя линия трапеции равна полусумме оснований. Полусумма оснований трапеции (ABCD) составляет (0,8) одного из оснований, тогда сумма оснований трапеции (ABCD) составляет (2cdot 0,8 = 1,6) этого основания, обозначим его за (AD). Тогда (BC + AD = 1,6AD), откуда (BC = 0,6AD). Средняя линия равна (0,8AD), тогда отношение длины основания (BC) к длине средней линии равно (0,6 : 0,8 = 0,75).

Ответ: 0,75


Задание
6

#294

Уровень задания: Равен ЕГЭ

Основания (AD) и (BC) трапеции (ABCD) равны соответственно (20) и (12), одна из боковых сторон равна (10), площадь трапеции (ABCD) равна (80). Найдите острый угол трапеции (ABCD), который образует эта боковая сторона с одним из оснований. Ответ дайте в градусах.

Пусть (AB = 10), (BE) – перпендикуляр к (AD), точка (E) лежит на (AD).

Площадь трапеции равна произведению полусуммы оснований на высоту, тогда (80 = 0,5(20 + 12)cdot BE).

(BE = 5 = 0,5cdot AB). Треугольник (ABE), – прямоугольный, причём (BE = 0,5cdot AB), тогда угол, лежащий против катета (BE), равен (30^{circ}).

(angle BAE = 30^{circ}) – единственный острый угол трапеции (ABCD), который образует (AB) с одним из оснований.

Ответ: 30


Задание
7

#1693

Уровень задания: Равен ЕГЭ

В трапеции (ABCD) диагонали пересекаются в точке (O). Площадь (triangle AOD) относится к площади (triangle ODC), как (8:3). В каком отношении состоит меньшее основание (BC) трапеции (ABCD) к большему основанию (AD)?

Высота, опущенная из вершины (D) на сторону (AO) в (triangle AOD) и на сторону (OC) в (triangle ODC) будет одной и той же. Значит, (frac{S_{triangle DOC}}{S_{triangle AOD}} = frac{OC}{AO} = frac{BC}{AD} = frac{3}{8} = 0,375).

Ответ: 0,375

Всем выпускникам, которые готовятся к сдаче ЕГЭ по математике, будет полезно освежить в памяти тему «Произвольная трапеция». Как показывает многолетняя практика, планиметрические задачи из этого раздела вызывают у многих старшеклассников определенные сложности. При этом решить задачи ЕГЭ на тему «Произвольная трапеция» требуется при прохождении и базового, и профильного уровня аттестационного испытания. Следовательно, уметь справляться с подобными упражнениями должны все выпускники.

Как подготовиться к экзамену?

Большинство планиметрических задач решаются путем классических построений. Если в задаче ЕГЭ требуется найти, к примеру, площадь трапеции, изображенной на рисунке, стоит отметить на чертеже все известные параметры. После этого вспомните основные теоремы, относящиеся к ним. Применив их, вы сможете найти правильный ответ.

Чтобы подготовка к экзамену была действительно эффективной, обратитесь к образовательному порталу «Школково». Здесь вы найдете весь базовый материал по темам «Произвольная трапеция или «Равнобедренная трапеция», который поможет вам успешно сдать ЕГЭ. Основные свойства фигуры, формулы и теоремы собраны в разделе «Теоретическая справка».

«Прокачать» навыки решения задач выпускники смогут также на нашем математическом портале. В разделе «Каталог» представлена большая подборка соответствующих упражнений разного уровня сложности. Перечень заданий наши специалисты регулярно обновляют и дополняют.

Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник

Всего: 36    1–20 | 21–36

Добавить в вариант

Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.

Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45°.

Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.

Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.

Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.

Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.

Основания равнобедренной трапеции равны 4 и 16, а ее боковые стороны равны 10. Найдите площадь трапеции.

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Площадь треугольника ABC равна 12. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.

План местности разбит на клетки. Каждая клетка обозначает квадрат 10 м × 10 м. Найдите площадь участка, изображённого на плане. Ответ дайте в м2.

План местности разбит на клетки. Каждая клетка обозначает квадрат 10 × 10 м. Найдите площадь участка, изображённого на плане. Ответ дайте в м2.

Источник: Ти­по­вые те­сто­вые за­да­ния по ма­те­ма­ти­ке, под ре­дак­ци­ей И. В. Ящен­ко. 2015 г.

Площадь трапеции S в м2 можно вычислить по формуле S= дробь: числитель: a плюс b, знаменатель: 2 конец дроби умножить на h, где a, b  — основания трапеции, h  — высота (в метрах). Пользуясь этой формулой, найдите S, если a = 5, b = 3 и h = 6.

Площадь трапеции S в м2 можно вычислить по формуле S= дробь: числитель: a плюс b, знаменатель: 2 конец дроби умножить на h, где a, b  — основания трапеции, h  — высота (в метрах). Пользуясь этой формулой, найдите S, если a = 4, b = 9 и h = 2.

Площадь трапеции S в м2 можно вычислить по формуле S= дробь: числитель: a плюс b, знаменатель: 2 конец дроби умножить на h, где a, b  — основания трапеции, h  — высота (в метрах). Пользуясь этой формулой, найдите S, если a = 6, b = 4 и h = 6.

Площадь трапеции S в м2 можно вычислить по формуле S= дробь: числитель: a плюс b, знаменатель: 2 конец дроби умножить на h, где a, b  — основания трапеции, h  — высота (в метрах). Пользуясь этой формулой, найдите S, если a = 3, b = 6 и h = 4.

Основания трапеции равны 16 и 22, боковая сторона, равная 10, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.

Всего: 36    1–20 | 21–36

Источник

25
Июл 2013

Категория: Справочные материалы

Трапеция. Свойства трапеции

2013-07-25
2016-06-15

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

виды трапеций

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.

равнобедренная трапеция

Трапеция,  у которой есть  прямые углы при боковой стороне, называется прямоугольной.

прямоугольная трапеция

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

средняя линия

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

свойство средней линии трапеции

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

биссектриса в трапеции

3. Треугольники AOD и COB, образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия – k=frac{AD}{BC}.

Отношение площадей этих треугольников есть k^2.

57

4. Треугольники ABO и DCO, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

свойства трапеции, равновеликие треугольники

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

окружность, вписанная в трапецию

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

qk

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

е

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

трапеция с углами при основании в сумме 90

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

свойства равнобедренной трапеции

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

трапеция вписана в окружность

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

диагонали трапеции перпендикулярны

Вписанная  окружность

Если в трапецию вписана окружность с радиусом r  и она делит боковую сторону точкой касания на два отрезка — a и b,  то r=sqrt{ab}.

4

Площадь

S=frac{a+b}{2}cdot h или S=lh, где  l – средняя линия

площадь трапеции

Смотрите хорошую подборку  задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Смотрите также площадь трапеции.

Автор: egeMax |

комментарий 431

Печать страницы

Источник

Задание 972

Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

Ответ: 30

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Площадь трапеции вычисляется по формуле $$S=frac{a+b}{2}*h$$. Получаем $$40=frac{7+13}{2}*CH$$. Отсюда CH = 4.

Из треугольника CHD по теореме Пифагора находим CD = 5. Отсюда периметр равен 7 + 13 + 5 + 5 = 30

Задание 1858

Най­ди­те боль­ший угол рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль AC об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной AB углы, рав­ные 30° и 45° со­от­вет­ствен­но.

Ответ: 105

Скрыть

$$angle A=angle BAC+angle CAD=30+45=75^{circ}$$, тогда по свойству углов трапеции: $$angle B=180-angle A=105^{circ}$$

Задание 1859

Най­ди­те угол АDС рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем ВС и бо­ко­вой сто­ро­ной АВ углы, рав­ные 30° и 50° со­от­вет­ствен­но.

Ответ: 80

Скрыть

$$angle A=angle BAC+angle CAD=30+50=80^{circ}$$

Задание 1860

Сумма двух углов рав­но­бед­рен­ной тра­пе­ции равна 140°. Най­ди­те боль­ший угол тра­пе­ции. Ответ дайте в гра­ду­сах.

Ответ: 110

Скрыть

Так как дана равнобедренная трапеция, то сумма острых углов при большем основании будет составлять 140 градусов, $$angle A=angle B=frac{140}{2}=70^{circ}$$, по свойству углов трапеции: $$angle D=180-angle A=110^{circ}$$

Задание 1861

Най­ди­те мень­ший угол рав­но­бед­рен­ной тра­пе­ции, если два ее угла от­но­сят­ся как 1:2. Ответ дайте в гра­ду­сах.

Ответ: 60

Скрыть

Пусть меньший угол равен х, тогда больший угол равен 2х. По свойству углов трапеции получаем, что $$x+2x=180Leftrightarrow$$$$x=60$$, то есть меньший угол составляет $$60^{circ}$$

Задание 1863

Тан­генс остро­го угла пря­мо­уголь­ной тра­пе­ции равен $$frac{5}{6}$$. Най­ди­те её боль­шее ос­но­ва­ние, если мень­шее ос­но­ва­ние равно вы­со­те и равно 15.

Ответ: 33

Скрыть

Опустим высоту CF, тогда из прямоугольного треугольника CFB: $$FB=frac{CF}{tgB}=frac{15}{frac{5}{6}}=18$$. DC=AF=15, тогда AB=15+18=33.

Задание 1864

В рав­но­бед­рен­ной тра­пе­ции из­вест­ны вы­со­та 4, мень­шее ос­но­ва­ние 8 и угол при ос­но­ва­нии $$45^{circ}$$. Най­ди­те боль­шее ос­но­ва­ние.

Ответ: 16

Скрыть

Опустим высоты DE=CF=4, тогда из прямоугольного треугольника ADE: так как $$angle A=45^{circ}$$, то $$angle ADE=90-45=45^{circ}$$, следовательно, реугольник AED — равнобедренный, и AE=DE=4, аналогично FB=4. Но EF=DC=8, тогда AB=4+4+8=16.

Задание 1865

Ос­но­ва­ния тра­пе­ции равны 4 и 10. Най­ди­те боль­ший из от­рез­ков, на ко­то­рые делит сред­нюю линию этой тра­пе­ции одна из её диа­го­на­лей.

Ответ: 5

Скрыть

EG — средняя линия треугольника ADB, тогда $$EG=frac{1}{2}=AB=5$$, аналогично GF — средняя линия треугольника DCB, тогда $$GF=frac{1}{2}DC=2$$, наибольший в таком случае равен 5

Примечение: больший из отрезков всегда будет равен половине большего основания

Задание 1866

Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 50 и 104, бо­ко­вая сто­ро­на 45. Най­ди­те длину диа­го­на­ли тра­пе­ции.

Ответ: 85

Скрыть

Опустим две высоты DE=CF, тогда AE=FB (из равенства прямоугольных треугольников ADE и CFB по катету и гипотенузе), и DC=EF=50, тогда $$AE=FB=frac{104-50}{2}=27$$. Тогда из прямоугольного треугольника ADE : $$DE=sqrt{AD^{2}-AE^{2}}=sqrt{45^{2}-27^{2}}=36$$, следовательно, EB=AB-AE=104-27=77. Тогда из прямоугольного треугольника DEB: $$DB=sqrt{DE^{2}+EB^{2}}=sqrt{77^{2}+36^{2}}=85$$

Задание 1867

Около тра­пе­ции, один из углов ко­то­рой равен 49°, опи­са­на окруж­ность. Най­ди­те осталь­ные углы тра­пе­ции.

За­пи­ши­те ве­ли­чи­ны углов в ответ через точку с за­пя­той в по­ряд­ке не­убы­ва­ния.

Ответ: 49; 131; 131

Скрыть

По свойству вписанного четырехугольник $$angle A+angle C=180^{circ}$$, пусть $$angle A=49^{circ}Rightarrow$$$$angle C=180-49=131^{circ}$$. По свойству углов трапеции $$angle B=180-angle C=180-131=49^{circ}$$, аналогично $$angle D=180-angle A=131^{circ}$$

Задание 1868

В тра­пе­цию, сумма длин бо­ко­вых сто­рон ко­то­рой равна 24, впи­са­на окруж­ность. Най­ди­те длину сред­ней линии тра­пе­ции.

Ответ: 12

Скрыть

По свойству описанного четырехугольника AD+BC=AB+CD, тогда сумма оснований тоже 24, средняя линия же равна полусумме оснований, то есть 24/2=12.

Задание 1965

Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна 6, а синус угла между ней и одним из ос­но­ва­ний равен $$frac{1}{3}$$. Най­ди­те пло­щадь тра­пе­ции.

Ответ: 30

Скрыть

  1. Опустим высоту CE. Пусть $$sin D=frac{1}{3}$$, тогда из прямоугольного треугольника CED: $$CE=CD*sin D=2$$
  2. Из формулы площади трапеции: $$S_{ABCD}=frac{18+12}{2}*2=30$$

Задание 1966

Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна 6, а ко­си­нус угла между ней и одним из ос­но­ва­ний равен $$frac{2sqrt{2}}{3}$$. Най­ди­те пло­щадь тра­пе­ции.

Ответ: 30

Скрыть

  1. Пусть $$cos D =frac{2sqrt{2}}{3}$$, опустим высоту CE. Тогда из треугольника  CED: $$ED=CD*cos D=6*frac{2sqrt{2}}{3}=4sqrt{2}$$
  2. По теореме Пифагора из треугольника CED: $$CE=sqrt{6^{2}-(4sqrt{2})^{2}}=2$$
  3. Из формулы площади трапеции $$S_{ABCD}=frac{18+12}{2}*2=30$$

Задание 1967

Сред­няя линия тра­пе­ции равна 11, а мень­ше ос­но­ва­ние равно 5. Най­ди­те боль­шее ос­но­ва­ние тра­пе­ции.

Ответ: 17

Скрыть

Пусть a — большее основание, тогда из формулы длины средней линии трапеции : $$a=2*11-5=17$$

Задание 1968

Бо­ко­вая сто­ро­на тра­пе­ции равна 5, а один из при­ле­га­ю­щих к ней углов равен 30°. Най­ди­те пло­щадь тра­пе­ции, если её ос­но­ва­ния равны 3 и 9.

Ответ: 15

Скрыть

  1. Пусть $$angle D=30^{circ}$$. Опустим высоту CE, тогда из прямоугольного треугольника CED: $$CE=CD*sin D=2,5$$
  2. По формуле площади трапеции $$S_{ABCD}=frac{3+9}{2}*2,5=15$$

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти сколько квартир в доме
  • Гардероб на работу как составить
  • Как найти свои апл вотч с айфона
  • Как составить конъюнктуру
  • Как найти qr код своего компьютера