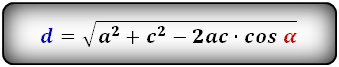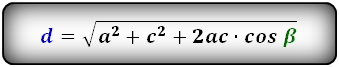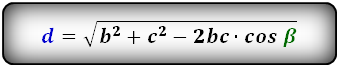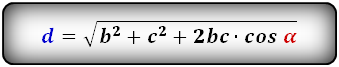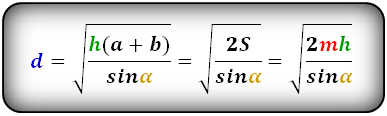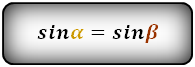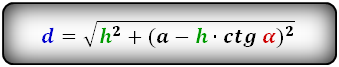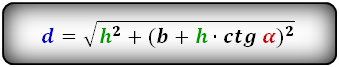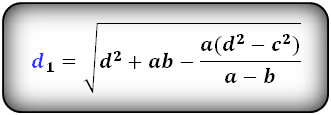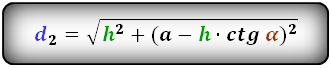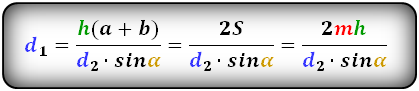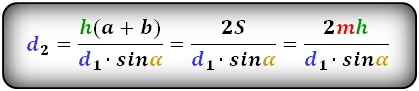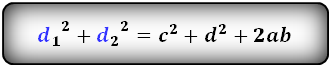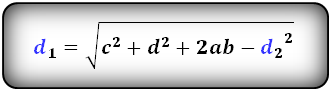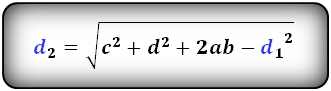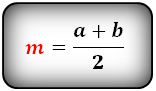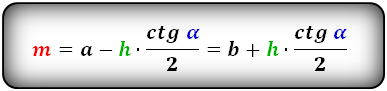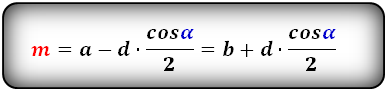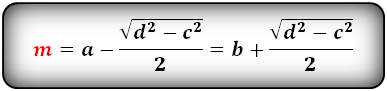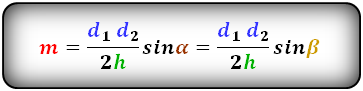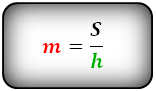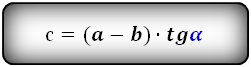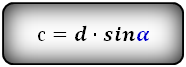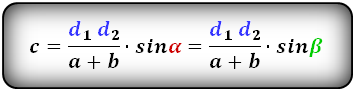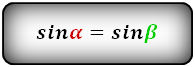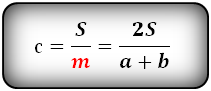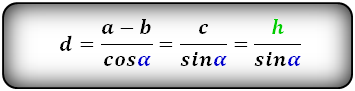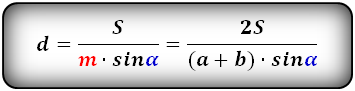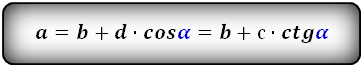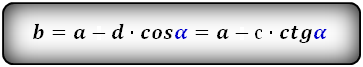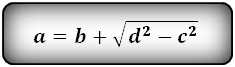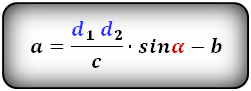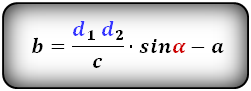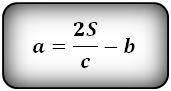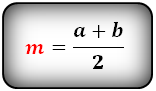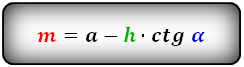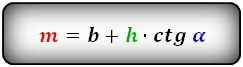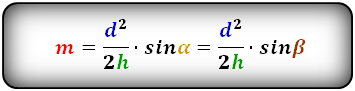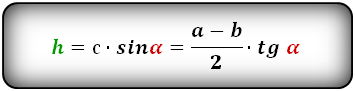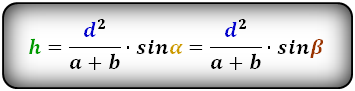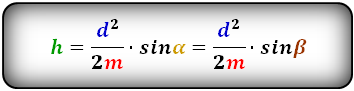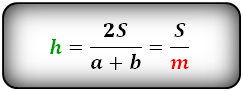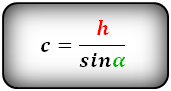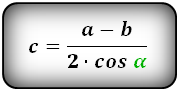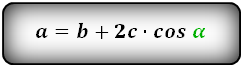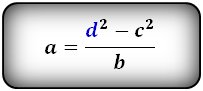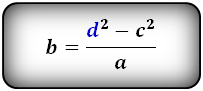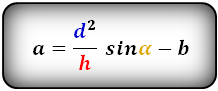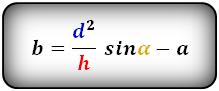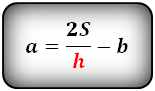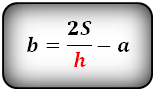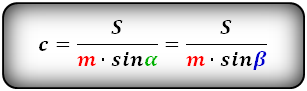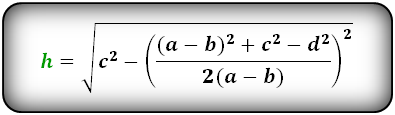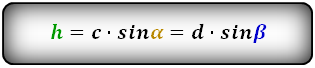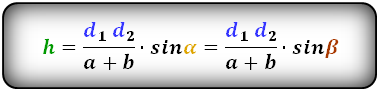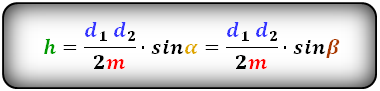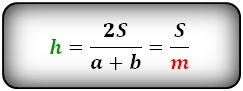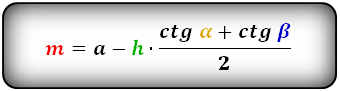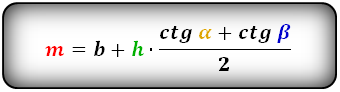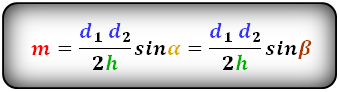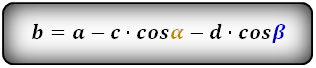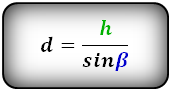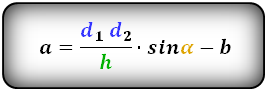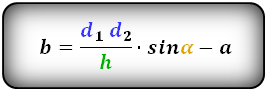{S = dfrac{1}{2} (a + b) cdot h}
Площадь трапеции можно найти множеством способов. Для вас мы собрали все возможные варианты нахождения площади. Для вашего удобства для каждой формулы создан калькулятор, который поможет рассчитать площадь трапеции по известным данным. От вас требуется только подставить значения и в режиме онлайн мгновенно получить ответ. Формулы и калькуляторы сгруппированы по типам трапеций — обычная, равнобедренная (равнобокая).
- Калькулятор площади трапеции
- Площадь трапеции
- через основания и высоту
- через среднюю линию и высоту
- через диагонали и среднюю линию
- через 4 стороны
- через диагонали и угол между ними
- через основания и углы при основании
- через площади треугольников
- через диагонали и высоту
- через радиус вписанной окружности и основания
- через перпендикулярные диагонали
- Площадь равнобедренной (равнобокой) трапеции
- через основания и высоту
- через 3 стороны (формула Брахмагупты)
- через верхнее основание, боковую сторону и угол при нижнем основании
- через нижнее основание, боковую сторону и угол при нижнем основании
- через основания и угол
- через диагонали и угол между ними
- через боковую сторону, угол при основании и среднюю линию
- через радиус вписанной окружности и угол при основании
- Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
- через высоту (диаметр вписанной окружности) и угол при основании
- через основания и угол при основании
- через основания и радиус вписанной окружности
- через основания
- через основания и боковую сторону
- через основания и среднюю линию
- Примеры задач
Площадь трапеции
Трапеция — выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
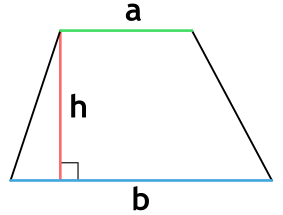
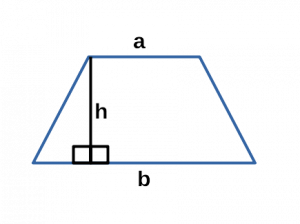
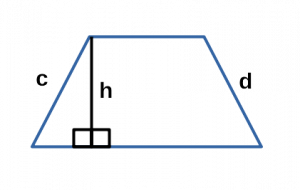
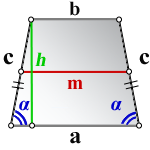
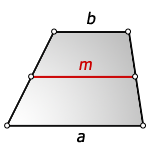
Площадь трапеции через основания и высоту
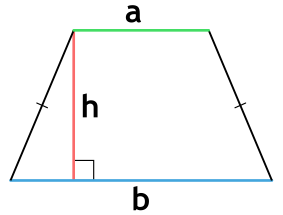
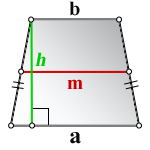
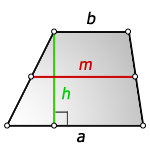
{S = dfrac{1}{2} (a + b) cdot h}
a и b — основания трапеции
h — высота, проведенная к основанию
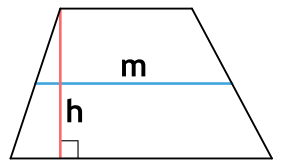
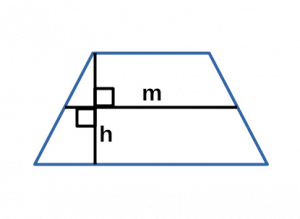
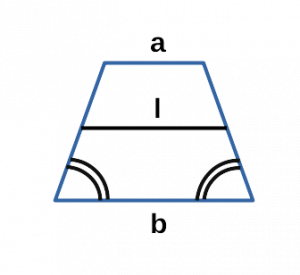
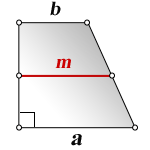
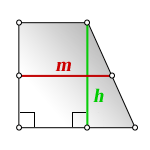
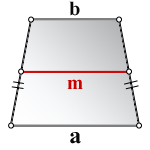
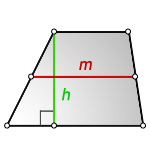
Площадь трапеции через среднюю линию и высоту
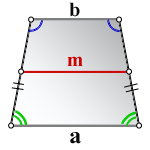
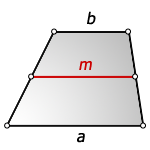
{S = m cdot h}
m — средняя линия трапеции
h — высота трапеции
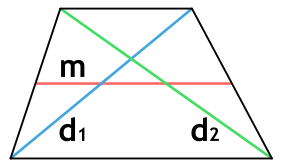
Площадь трапеции через диагонали и среднюю линию
{S = sqrt{p(p-d_1)(p-d_2)(p-2m)}}
{p = dfrac{d_1+d_2+2m}{2}}
d1 и d2 — диагонали трапеции
m — средняя линия трапеции
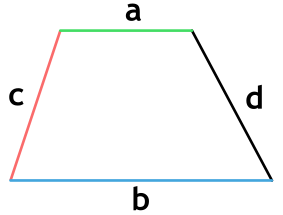
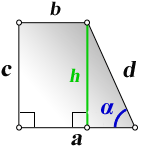
Площадь трапеции через 4 стороны
{S = dfrac{a+b}{2} sqrt{c^2 — {Big( dfrac{(a-b)^2 + c^2 — d^2}{2(a-b)} Big)}^2}}
a, b, c и d — стороны трапеции
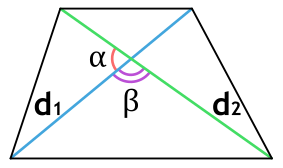
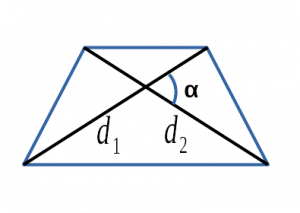
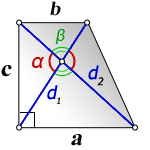
Площадь трапеции через диагонали и угол между ними
{S = dfrac{d_1 cdot d_2}{2}cdot sin(alpha); S = dfrac{d_1 cdot d_2}{2}cdot sin(beta)}
d1 и d2 — диагонали трапеции
α или β — угол между диагоналями трапеции
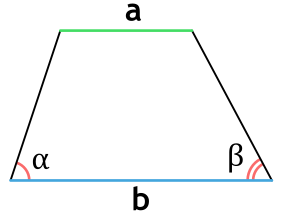
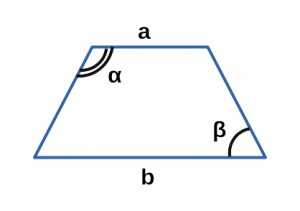
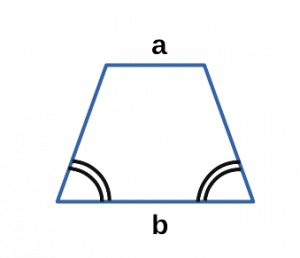
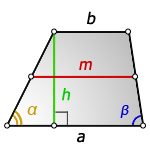
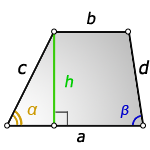
Площадь трапеции через основания и углы при основании
{S = dfrac{b^2 — a^2}{2} cdot dfrac{sin(alpha) cdot sin(beta)}{sin(alpha + beta)}}
a и b — основания трапеции
α или β — прилежащие к основанию трапеции углы
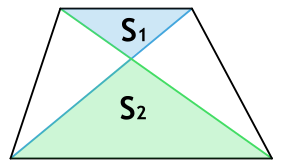
Площадь трапеции через площади треугольников
{S = (sqrt{S_1} + sqrt{S_2})^2}
S1 и S2 — площади образованных пересечением диагоналей трапеции треугольников
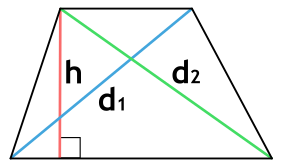
Площадь трапеции через диагонали и высоту
{S = dfrac{sqrt{{d_2}^2-h^2}+sqrt{{d_1}^2-h^2}}{2} cdot h}
d1 и d2 — диагонали трапеции
h — высота трапеции
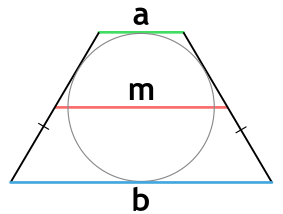
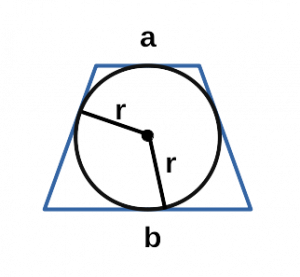
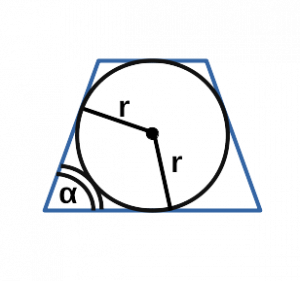
Площадь трапеции через радиус вписанной окружности и основания
{S = (a+b)cdot r}
a и b — основания трапеции
r — радиус вписанной в трапецию окружности
Площадь трапеции через перпендикулярные диагонали
{S = dfrac{1}{2} cdot d_1 cdot d_2}
d1 и d2 — перпендикулярные диагонали трапеции
Площадь равнобедренной (равнобокой) трапеции
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
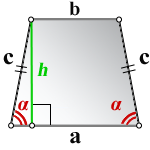
Площадь равнобедренной трапеции через основания и высоту
{S = dfrac{a+b}{2} cdot h}
a и b — основания равнобедренной трапеции
h — высота, проведенная к основанию равнобедренной трапеции
Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)
{S = sqrt{(p-a)(p-b)(p-c)^2}}
{p = dfrac{a+b+2c}{2}}
a и b — основания равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
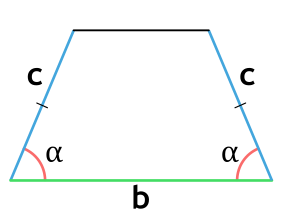
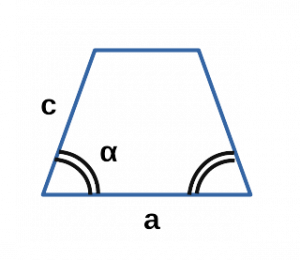
Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании
{S = c cdot sin(alpha) cdot (a+c cdot cos(alpha))}
a — верхнее основание равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
α — прилежащие к нижнему основанию трапеции углы
Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании
{S = c cdot sin(alpha) cdot (b-c cdot cos(alpha))}
b — нижнее основание равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
α — прилежащий к нижнему основанию трапеции угол
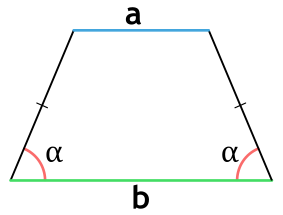
Площадь равнобедренной трапеции через основания и угол
{S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha)}
a и b — основания равнобедренной трапеции
α — прилежащий к основанию трапеции угол
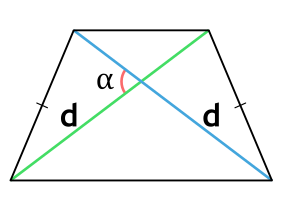
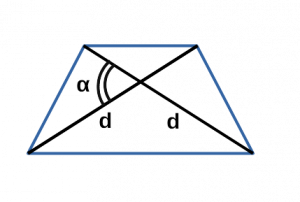
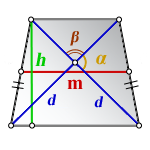
Площадь равнобедренной трапеции через диагонали и угол между ними
{S = dfrac{1}{2}d^2 cdot sin(alpha)}
a — диагональ равнобедренной трапеции
α — угол между диагоналями равнобедренной трапеции
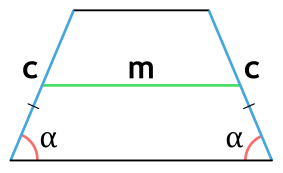
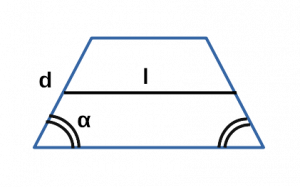
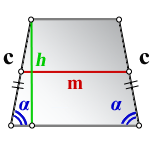
Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию
{S = m cdot c cdot sin(alpha)}
m — средняя линия равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
α — угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании
{S = dfrac{4r^2}{sin(alpha)}}
r — радиус вписанной окружности
α — угол при основании равнобедренной трапеции
Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
В трапецию можно вписать окружность тогда и только тогда, когда суммы ее противоположных сторон равны.
Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании
{S = dfrac{h^2}{sin(alpha)}}
h — высота равнобедренной трапеции
α — угол при основании равнобедренной трапеции
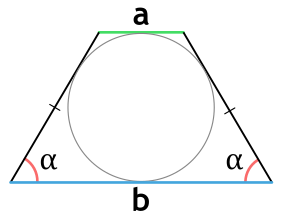
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании
{S = dfrac{a cdot b}{sin(alpha)}}
a и b — основания равнобедренной трапеции
α — угол при основании равнобедренной трапеции
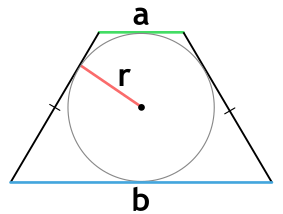
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности
{S = r(a+b); r=dfrac{sqrt{a cdot b}}{2}}
a и b — основания равнобедренной трапеции
r — радиус вписанной окружности
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания
{S = sqrt{a cdot b} cdot dfrac{a+b}{2}}
a и b — основания равнобедренной трапеции
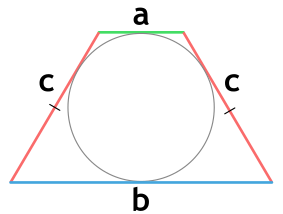
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону
{S = c cdot sqrt{a cdot b}}
a и b — основания равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию
{S = m cdot sqrt{a cdot b}}
a и b — основания равнобедренной трапеции
m — средняя линия равнобедренной трапеции
Примеры задач на нахождение площади трапеции
Задача 1
Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.
Решение
Для решения задачи воспользуемся первой формулой.
S = dfrac{1}{2} (a + b) cdot h = dfrac{1}{2} (6 + 9) cdot 5 = dfrac{1}{2} cdot 15 cdot 5 = dfrac{1}{2} cdot 75 = 37dfrac{1}{2} : см^2
Ответ: 37.5 см²
Полученный ответ легко проверить с помощью калькулятора .
Задача 2
Найдите площадь трапеции средняя линия которой равна 18 см, а высота 9 см.
Решение
С решением этой задачи нам поможет вторая формула.
S = m cdot h = 18 cdot 9 = 162 : см^2
Ответ: 162 см²
Воспользуемся калькулятором для проверки результата.
Задача 3
Найдите площадь трапеции диагонали которой равны 10 и 8, а средняя линия равна 3.
Решение
Для решения этой задачи нам поможет третья формула.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{10+8+2 cdot 3}{2} = dfrac{10+8+6}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-10)(12-8)(12-2 cdot 3)} = sqrt{12 cdot 2 cdot 4 cdot 6} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Осталось проверить полученный ответ.
Задача 4
Найдите площадь трапеции диагонали которой равны 17 и 15, а средняя линия равна 4.
Решение
Задача похожа на ту, что мы только что решили. Поэтому повторим шаги.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{17+15+ 2 cdot 4}{2} = dfrac{17+15+8}{2} = dfrac{40}{2} = 20
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{20(20-17)(20-15)(20-2 cdot 4)} = sqrt{20 cdot 3 cdot 5 cdot 12} = sqrt{3600} = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 5
Найдите площадь трапеции диагонали которой равны 8 и 6 а средняя линия равна 5.
Решение
Еще одна типовая задача. Повторим действия как в задачах выше.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{8+6+ 2 cdot 5}{2} = dfrac{8+6+10}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-8)(12-6)(12-2 cdot 5)} = sqrt{12 cdot 4 cdot 6 cdot 2} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Проверка .
Задача 6
Найдите площадь равнобедренной трапеции если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.
Решение
Для решения этой задачи используем формулу Брахмагупты.
Сначала вычислим p:
p = dfrac{a+b+2c}{2} = dfrac{5+17+2 cdot 10}{2} = dfrac{22+20}{2} = dfrac{42}{2} = 21
А теперь можно вычислить площадь трапеции:
S = sqrt{(p-a)(p-b)(p-c)^2} = sqrt{(21-5)(21-17)(21-10)^2} = sqrt{16 cdot 4 cdot 11^2} = sqrt{16 cdot 4 cdot 121} = sqrt{7744}= 88 : см^2
Ответ: 88 см²
Проверка .
Задача 7
Острый угол равнобедренной трапеции равен 45°, а основания равны 8 и 6 см. Найдите площадь трапеции.
Решение
Для решения этой задачи воспользуемся формулой.
S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha) = dfrac{1}{2}(8^2-6^2) cdot tg(45°)
Тангенс 45° = 1, продолжим вычисления:
S = dfrac{1}{2}(8^2-6^2) cdot tg(45°) = dfrac{1}{2}(64-36) cdot 1 = dfrac{1}{2} cdot 28 = 14 : см^2
Ответ: 14 см²
Убедиться в правильности решения нам поможет калькулятор .
Выбирайте формулу в зависимости от известных величин.
1. Как найти площадь трапеции через основания и высоту
Посчитайте сумму оснований трапеции.
Умножьте результат на высоту и поделите на два.
- S – искомая площадь трапеции.
- a и b – основания трапеции (её параллельные стороны).
- h – высота трапеции.
2. Как вычислить площадь трапеции через высоту и среднюю линию
Просто умножьте высоту трапеции на среднюю линию.
- S – искомая площадь трапеции.
- m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
- h – высота трапеции.
3. Как найти площадь трапеции через диагонали и угол между ними
Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.
Поделите результат на два.
- S – искомая площадь трапеции.
- x и y – диагонали трапеции.
- α – любой угол между диагоналями.
4. Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
- S – искомая площадь трапеции.
- a, b – основания трапеции.
- c, d – боковые стороны.
5. Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
- S — искомая площадь трапеции.
- a, b — основания трапеции.
- c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).
6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол
Найдите квадрат радиуса и умножьте его на четыре.
Поделите результат на синус известного угла.
- r — радиус вписанной окружности.
- α — любой угол трапеции.
Читайте также 📐✏️🎓
- 8 способов найти длину окружности
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Площадь трапеции, формулы расчета, определение,
способы найти площадь, нахождение площади
через величины и примеры площади трапеции.
Все формулы расчета площади трапеции
через основания и угол, периметр, радиус,
синус и две стороны, диагональ,
высоту, среднюю линию.
Площадь трапеции, можно измерить, в единицах
измерения в квадрате: мм2, см2, м2 и км2 и так далее.
Площадь трапеции через окружность вписанную можно
найти, зная радиус окружности вписанной в трапецию
и некоторые другие величины.
Содержание
- Формулы площади трапеции
- Площадь любых трапеций
- Площадь равнобедренной трапеции
- Определения трапеции
- Элементы трапеции
Формулы площади трапеции
Площадь любых трапеций
Ⅰ. Площадь трапеции через основания и высоту:
[ S = frac{a+b}{2} cdot h ]
a,b — основания трапеции;
h — высота трапеции;
Ⅱ. Площадь трапеции через высоту и среднюю линию:
[ S = mh ]
m — средняя линия трапеции;
h — высота трапеции;
Ⅲ. Площадь трапеции через диагонали и угол между ними:
[ S =frac{1}{2}d_1d_2 cdot sin alpha ]
( d_1, d_2 )- диагонали трапеции;
sin α — синус угла альфа в трапеции;
Ⅳ. Площадь трапеции через периметр, высоту и боковые стороны:
[ S = frac{P-(c+d)}{2}h ]
P — периметр трапеции;
c,d — боковые стороны трапеции;
h — высота трапеции;
Ⅴ. Площадь трапеции через основания и боковые стороны:
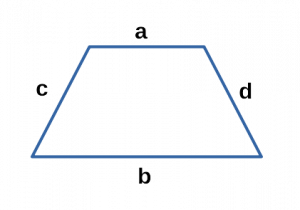
a,b — основания трапеции;
с,d — боковые стороны трапеции;
Ⅵ. Площадь трапеции через основания и углы:
[ S = frac{b^2-a^2}{2} cdot frac{sin α cdot sin β}{sin( α + β)} ]
a,b — основания трапеции;
α — угол при основании a в трапеции;
β — угол при основании b в трапеции;
sin α — синус угла альфа в трапеции;
sin β — синус угла бетта в трапеции;
Площадь равнобедренной трапеции
Ⅰ. Площадь трапеции через синус угла, среднюю линию и боковую сторону:
[ S = ld cdot sin α ]
l — средняя линия равнобедренной трапеции;
d — боковая сторона равнобедренной трапеции;
α — угол альфа при боковой стороне d равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Ⅱ. Площадь трапеции через диагонали и синус угла:
[ S = frac{d^2}{2} cdot sin α ]
d — диагональ равнобедренной трапеции;
α — угол между двумя диагоналями в равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Ⅲ. Площадь трапеции через радиус вписанной окружности и основания:
[ S = r( a+b) ]
r — радиус вписанной окружности равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
Ⅳ. Площадь трапеции через основания:
[ S = sqrt{ab} cdot {frac{a+b}{2}} ]
a, b — основания равнобедренной трапеции;
Ⅴ. Площадь трапеции через основания и среднюю линию:
[ S = lsqrt{ab} ]
l — средняя линия равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
Ⅵ. Площадь трапеции через синус угла и стороны:
[ S = c cdot sin α cdot (a-c cdot cos α) ]
a — нижнее основание равнобедренной трапеции;
с — боковая сторона равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
cos α — косинус угла альфа в равнобедренной трапеции;
Ⅶ. Площадь трапеции через угол и радиус вписанной окружности:
[ S = frac{4r^2}{sin α} ]
r — радиус вписанной окружности равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Определения трапеции
Трапеция — это четырехугольник, у которого две
стороны параллельны а две другие нет.
Зная углы трапеции, можно определить, к какому виду
она относится. Всего различают три вида трапеций:
- Обычная / стандартная трапеция: четыре угла и четыре стороны не равны.
- Равнобедренная / равнобочная / равнобоковая трапеция:
два угла при основании равны, две боковые стороны равны. - Прямоугольная / прямая трапеция: один из углов прямой.
Площадь равнобедренной, прямоугольной трапеции,
можно найти через формулы площади обычной трапеции.
Формул, с помощью которых, можно найти площадь трапеции
через описанную окружность около трапеции, не существует.
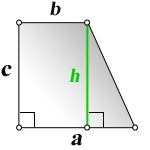
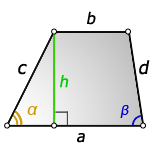
Элементы трапеции
Любая трапеция является четырехугольником,
поэтому у трапеции 4 угла и 4 стороны.
Основание трапеции — это сторона, противолежащая
сторона которой параллельна.
Боковая сторона трапеции — это сторона, противолежащая
сторона которой не параллельна.
Средняя линия трапеции — это отрезок, соединяющий
середины боковых сторон трапеции.
Диагональ трапеции — это отрезок, соединяющий две
вершины, которые лежат в разных концах трапеции.
Высота трапеции — это отрезок, соединяющий меньшее основание с большим,
образуя при этом два угла по 90 градусов на большей стороне.
Основания у трапеции не могут быть никогда равны.
Боковые стороны могут быть равны только,
если трапеция — равнобедренная.
Площадь трапеции — это площадь геометрической фигуры,
у которой четыре стороны и четыре угла, причем только
две стороны параллельны а остальные нет.
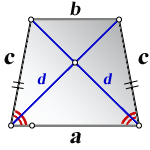
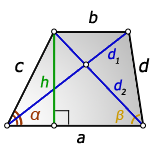
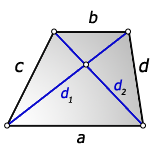
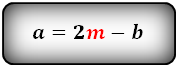
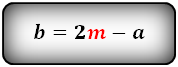
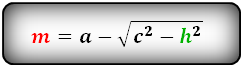
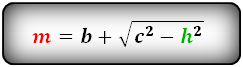
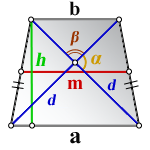
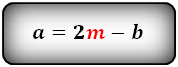
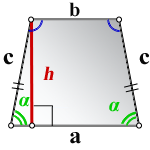
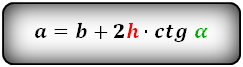
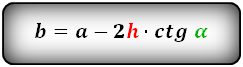
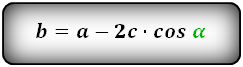
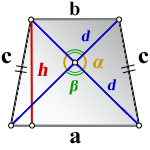
1. Формулы длины диагонали равнобедренной трапеции через ее стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагональ трапеции
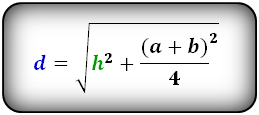
Формула диагонали трапеции (d ):
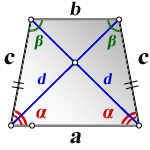
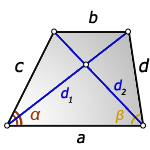
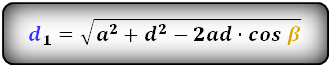
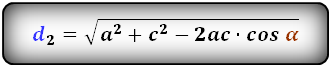
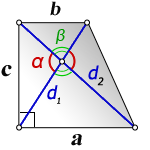
2. Формулы длины диагонали равнобедренной трапеции по теореме косинусов
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α, β — углы трапеции
d — диагональ трапеции
Формулы диагонали трапеции (d ):
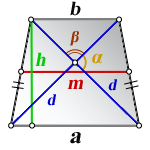
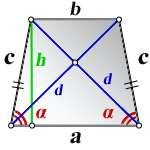
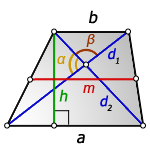
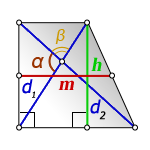
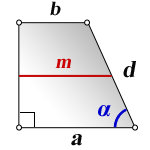
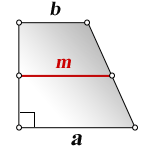
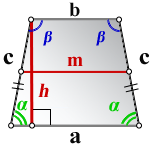
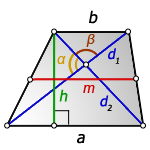
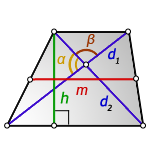
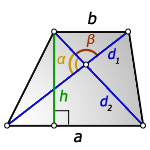
3. Формула длины диагонали равнобедренной трапеции
a — нижнее основание
b — верхнее основание
α, β — углы между диагоналями
h — высота трапеции
m — средняя линия трапеции
S — площадь трапеции
d — диагональ трапеции
Формулы диагонали трапеции (d ):
Справедливо для данного случая :
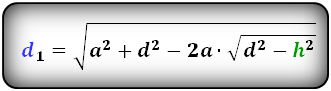
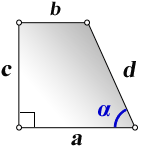
4. Формулы длины диагонали трапеции через высоту и стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
h — высота трапеции
α — угол при нижнем основании
d — диагональ трапеции
Формулы диагонали трапеции (d ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Найти длину диагонали трапеции
зная все четыре стороны
или две стороны и угол
или высоту, сторону и угол
или площадь, другую диагональ и угол
и еще много других формул.
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции по теореме косинусов:
Формулы диагоналей трапеции через четыре стороны:
2. Формула длины диагоналей трапеции через высоту
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции через высоту:
3. Формула длины диагонали трапеции через другую диагональ
a — нижнее основание
b — верхнее основание
α, β — углы между диагоналями
h — высота трапеции
m — средняя линия трапеции
S — площадь трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции :
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
d1 , d2 — диагонали трапеции
Формула суммы квадратов диагоналей :
Формулы диагоналей трапеции :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула средней линии трапеции через основания (для всех видов трапеции)
a — нижнее основание
b — верхнее основание
m — средняя линия
Формула средней линии, (m ):
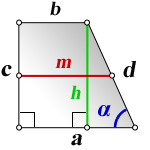
2. Формулы средней линии через основания, высоту и угол при нижнем основании
a, b — основания трапеции
c — боковая сторона под прямым углом к основаниям
d — боковая сторона
α — угол при основании
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
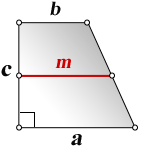
4. Формула средней линии трапеции через площадь и высоту (для всех видов трапеции)
S — площадь трапеции
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
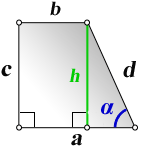
1. Формула боковой стороны (с) прямоугольной трапеции через другие стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
d — боковая сторона
α — угол при нижнем основании
h — высота трапеции
c — боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с) :
2. Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
c — боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с):
3. Формулы боковой стороны (с) прямоугольной трапеции через площадь
a — нижнее основание
b — верхнее основание
m — средняя линия трапеции
c — боковая сторона под прямым углом к основаниям
Формула длины боковой стороны (с) :
4. Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
α — угол при нижнем основании
h — высота трапеции
d — боковая сторона
Формулы длины боковой стороны (d) :
5. Формула боковой стороны (d) прямоугольной трапеции через площадь
a — нижнее основание
b — верхнее основание
m — средняя линия трапеции
α — угол при нижнем основании
d — боковая сторона
Формула длины боковой стороны (d) :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
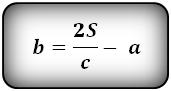
1. Формула длины оснований прямоугольной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
2. Формулы длины оснований через боковые стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α — угол при нижнем основании
Формулы длины оснований :
3. Формулы длины оснований трапеции через диагонали и угол между ними
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
Формулы длины оснований :
4. Формулы длины оснований трапеции через площадь
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
h — высота трапеции
Формулы длины оснований :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула средней линии равнобедренной трапеции через основания
a — нижнее основание
b — верхнее основание
m — средняя линия
Формула средней линии, (m ):
2. Формулы средней линии через основание, высоту и углы при нижнем основании
a — нижнее основание
b — верхнее основание
c — боковая сторона
α — угол при нижнем осровании
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
d — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m ):
4. Формула средней линии трапеции через площадь и высоту
S — площадь трапеции
h — высота трапеции
α — угол при нижнем осровании
m — средняя линия
Формула средней линии трапеции, (m ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула высоты равнобедренной трапеции через стороны и углы при основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при нижнем основании
h — высота трапеции
Формулы длины высоты, (h ):
2. Формула высоты равнобедренной трапеции через диагонали и углы между ними
d — диагонали трапеции
α , β — углы между диагоналями
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
3. Формула высоты равнобедренной трапеции через площадь
S — площадь трапеции
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула длины основания равнобедренной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины основания:
2. Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.
1. Формула высоты трапеции через стороны и углы при основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы длины высоты, (h ):
2. Формула высоты трапеции через диагонали и углы между ними
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
3. Формула высоты трапеции через площадь
S — площадь трапеции
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции — отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.
1. Формула средней линии трапеции через основания
b — верхнее основание
a — нижнее основание
m— средняя линия
Формула средней линии, (m ):
2. Формулы средней линии через основание, высоту и углы при нижнем основании
b — верхнее основание
a — нижнее основание
α, β — углы трапеции
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
α, β — углы между диагоналями
d1 , d2 — диагонали трапеции
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
4. Формула средней линии трапеции через площадь и высоту
S — площадь трапеции
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
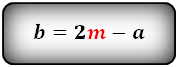
1. Формула длины основания трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
2. Формулы длины сторон через высоту и углы при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
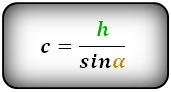
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Задания
Версия для печати и копирования в MS Word
Тип 17 № 350132
Основания трапеции равны 5 и 40, одна из боковых сторон равна 14, а косинус угла между ней и одним из оснований равен Найдите площадь трапеции.
Спрятать решение
Решение.
Пусть дана трапеция ABCD, где AD = 40, BC = 5, AB = 14, а
Опустим перпендикуляр BH на сторону AD. Найдем синус угла из основного тригонометрического тождества:
Найдем высоту BH:
Площадь трапеции равна полусумме оснований на высоту:
Ответ: 252.
Аналоги к заданию № 169883: 169884 169885 324155 … Все
Спрятать решение
·
Прототип задания
·
Помощь