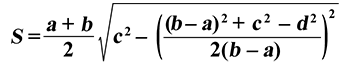Как найти площадь трапеции калькулятор онлайн - Исправление недочетов и поиск решений вместе с Examum.ru

Как рассчитать площадь трапеции

На данной странице калькулятор поможет рассчитать площадь трапеции онлайн. Для расчета задайте высоту и длуну основания трапеции.

Трапеция — четырёхугольник, у которого две стороны параллельны (основания трапеции), а две другие — непараллельны (боковые стороны трапеции). Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Через основания и высоту
Через среднюю линию и высоту
Через четыре стороны
Через диагонали и угол между ними
Через среднюю линию, боковую сторону и угол при основаниии
Через радиус вписанной окружности

Через основания и высоту

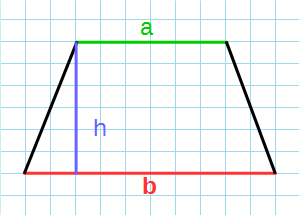
Формула для нахождения площади трапеции через основания и высоту:

a,b — основания трапеции; h — высота трапеции.

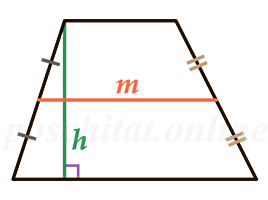
Через среднюю линию и высоту

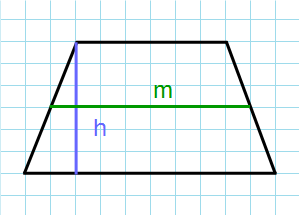
Формула для нахождения площади трапеции через основания и среднюю линию:

m — средняя линия; h — высота трапеции.

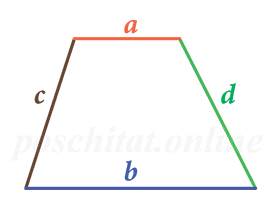
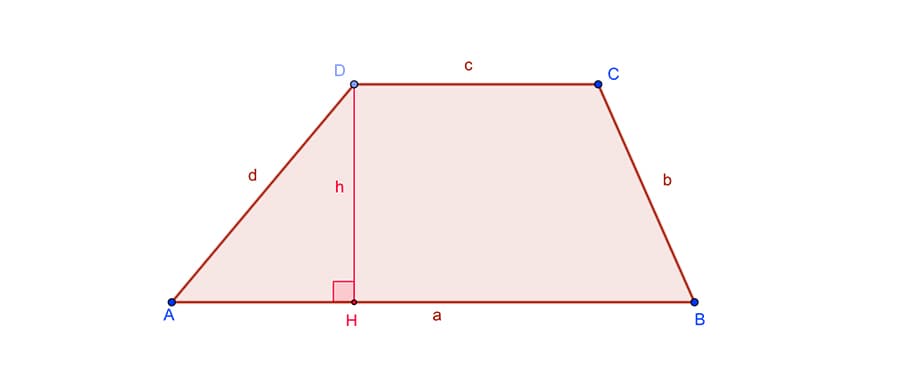
Через четыре стороны

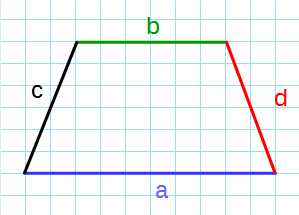
Формула для нахождения площади трапеции через основания и среднюю линию:

a — нижнее основание; b — верхнее основание; c, d — боковые стороны.

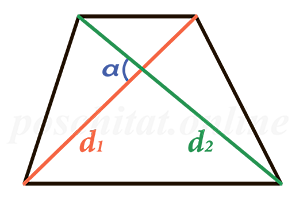
Через диагонали и угол между ними

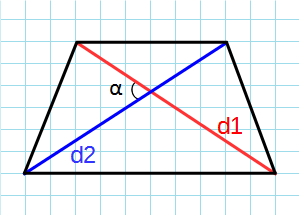
Формула для нахождения площади трапеции через диагонали и угол между ними:

d₁, d₂ — диагонали трапеции; α — угол между диагоналями.

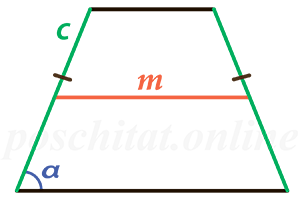
Через среднюю линию, боковую сторону и угол при основаниии

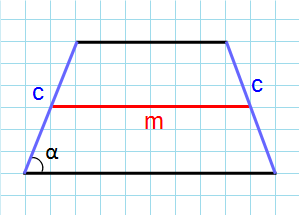
Формула для нахождения площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании:

m — средняя линия трапеции; c — боковая сторона трапеции; α — угол при основании.

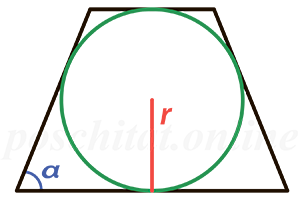
Через радиус вписанной окружности

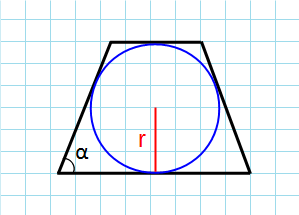
Формула для нахождения площади равнобедренной трапеции через радиус вписанной оккужности:

r — радиус окружности; α — угол при основании.

Источник

Площадь трапеции

Главная
/
Математика
/
Геометрия
/
Площадь трапеции

Чтобы найти площадь трапеции воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Через длины оснований и высоту

Чему равна площадь трапеции, если:

основание a =
основание b =
высота h =

Ответ: S =

ед.²

Округление ответа:

Чему равна площадь трапеции если известны основания a и b, а также высота h?

Формула

S = ½ ⋅ (a + b) ⋅ h

Пример

Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:

S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²

Через среднюю линию и высоту

Чему равна площадь трапеции, если:

средняя линия m =
высота h =

Ответ: S =

ед.²

Округление ответа:

Чему равна площадь трапеции если известны средняя линия m и высота h?

Формула

S = m ⋅ h

Пример

Если у трапеции средняя линия m = 6 см, а высота h = 4 см, то её площадь:

S = 6 ⋅ 4 = 24 см²

Через длины сторон и оснований

Чему равна площадь трапеции, если:

основание a =
основание b =
сторона c = сторона d =

Ответ: S =

ед.²

Округление ответа:

Чему равна площадь трапеции если известны основания a и b, а также стороны c и d?

Формула

Пример

Если у трапеции основание a = 2 см, основание b = 6 см, сторона c = 4 см, а сторона d = 7 см, то её площадь:

S ≈ 13.555 см²

Через диагонали и угол между ними

Чему равна площадь трапеции, если:

диагональ d₁ =
диагональ d₂ =
угол α =

Ответ: S =

ед.²

Округление ответа:

Чему равна площадь трапеции если известны диагонали d₁ и d₂ и угол между ними α?

Формула

S = ½ ⋅ d₁ ⋅ d₂ ⋅ sin(α)

Пример

Если у трапеции одна диагональ d₁ = 5 см, другая диагональ d₂ = 7 см, а угол между ними ∠α = 30°, то её площадь:

S = ½ ⋅ 5 ⋅ 7 ⋅ sin (30) = 17.5 ⋅ 0.5= 8.75 см²

Площадь равнобедренной трапеции

Через среднюю линию, боковую сторону и угол при основании

Чему равна площадь трапеции, если:

средняя линия m =
сторона c =
угол α =

Ответ: S =

ед.²

Округление ответа:

Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?

Формула

S = m ⋅ c ⋅ sin(α)

Пример

Если у равнобедренной трапеции средняя линия m = 6 см, сторона c = 4 см, а угол при основании ∠α = 30°, то её площадь:

S = 6 ⋅ 4 ⋅ sin (30) = 24 ⋅ 0.5 = 12 см²

Через радиус вписанной окружности

Чему равна площадь трапеции, если:

радиус r =
угол α =

Ответ: S =

ед.²

Округление ответа:

Чему равна площадь равнобедренной трапеции если радиус вписанной окружности r, a угол при основании α?

Формула

S = ^4⋅r² ⁄ _sin(α)

Пример

Если у равнобедренной трапеции радиус вписанной окружности r = 5 см, а угол при основании ∠α = 30°, то её площадь:

S = 4 ⋅ 5² / sin (30) = 100 / 0.5 = 200 см²

См. также

Источник

Оглавление:

📝 Как это работает?
🤔 Частые вопросы и ответы
📋 Похожие материалы
📢 Поделиться и комментировать

🤔 Что это за калькулятор?

Калькулятор площади трапеции — это веб-инструмент, который помогает рассчитать площадь трапеции на основе ее размеров, которые вводит пользователь. Обычно пользователю нужно указать длины двух параллельных сторон трапеции (оснований) и ее высоту.

Калькулятор площади трапеции может быть полезен при решении задач геометрии, в которых необходимо быстро вычислить площадь трапеции. Также он может использоваться при расчетах материалов для строительства и дизайна, где требуется знание площади поверхности трапеции.

🧮 Как работает калькулятор и какие есть примеры использования?

Работа калькулятора площади трапеции основана на формуле, которая используется для расчета площади трапеции. Формула для расчета площади трапеции выглядит следующим образом:

S = (a + b) * h / 2

Где «a» и «b» — это длины оснований трапеции, а «h» — ее высота.

Чтобы использовать калькулятор, пользователь должен ввести длины двух оснований трапеции и ее высоту в соответствующие поля веб-интерфейса калькулятора. После того, как пользователь ввел данные, калькулятор автоматически рассчитывает площадь трапеции и отображает результат на экране.

Пример

Разберем пример использования калькулятора на реальном объекте

Допустим, вы планируете купить ковер для своей гостиной комнаты, и вам нужно знать, какой размер ковра нужен. Ваша гостиная имеет форму трапеции, и вы не знаете, как рассчитать размер ковра, чтобы он идеально соответствовал форме комнаты.

В этом случае вы можете использовать калькулятор площади трапеции для определения площади поверхности пола в гостиной и, следовательно, определения размера ковра, который вам нужен.

Для этого вам необходимо измерить длины двух параллельных сторон комнаты (оснований) и ее высоту. Например, пусть одно основание комнаты равно 6 метров, а другое — 8 метров, а высота составляет 4 метра.

Вводим эти значения в соответствующие поля калькулятора площади трапеции, и получаем результат — площадь гостиной равна 28 квадратных метров.

Теперь вы можете использовать эту информацию, чтобы определить размер ковра, который вам нужен. Например, если вы решили приобрести ковер, покрывающий всю площадь комнаты, то вам понадобится ковер размером, равным 28 квадратных метров.

Также примеры использования калькулятора площади трапеции могут включать следующее:

Расчет площади трапеции в задачах геометрии на уроках в школе или вузе.
Расчет площади поверхности трапеции при планировании строительства, например, для расчета необходимого количества материалов.
Использование калькулятора при разработке дизайна или макетов, когда нужно знать площадь поверхности трапеции для правильного распределения элементов.
Расчет площади трапеции в повседневной жизни, например, при расчете площади участка земли или для определения площади поверхности торта или пиццы.

Какие виды трапеций существуют

Существует несколько видов трапеций, которые отличаются формой и свойствами сторон и углов. Вот некоторые из них:

Прямоугольная трапеция — это трапеция, у которой одно основание перпендикулярно к высоте. Углы между боковыми сторонами и основаниями равны по два, как и у прямоугольника.
Равнобокая трапеция — это трапеция, у которой боковые стороны равны друг другу. Углы между боковыми сторонами и основаниями не равны.
Равнобедренная трапеция — это трапеция, у которой две боковые стороны и углы между ними равны. Другие две стороны не являются равными и не равны углам между боковыми сторонами и основаниями.
Криволинейная трапеция — это трапеция, у которой боковые стороны не параллельны друг другу и имеют форму кривых линий.
Изогнутая трапеция — это трапеция, у которой одно или оба основания имеют изогнутую форму, но боковые стороны все еще параллельны.

Каждый вид трапеции имеет свои уникальные свойства, что делает их полезными в различных математических и геометрических задачах.

Площадь каких видов трапеций может рассчитать наш калькулятор?

Калькулятор площади трапеции может рассчитать площадь всех видов трапеций, включая прямоугольную, равнобокую, равнобедренную, криволинейную и изогнутую трапеции. Для расчета площади трапеции необходимо знать длины ее оснований и высоту. Если речь идет о криволинейной трапеции или изогнутой трапеции, то также необходимо знать длины наклонных боковых сторон.

Калькулятор площади трапеции учитывает все эти параметры и автоматически рассчитывает площадь трапеции, когда вы вводите соответствующие значения в поля веб-интерфейса калькулятора.

❓Вопросы и ответы

При расчете площади трапеции могут возникать различные вопросы. Вот некоторые из наиболее частых вопросов и ответы на них:

Как найти высоту трапеции, если она неизвестна?

Высота трапеции является перпендикулярной линией, проведенной от одного основания до другого. Если вы не знаете высоту, но знаете длины оснований и площадь трапеции, то можно использовать формулу S = (a + b)h/2, где S — площадь, a и b — длины оснований, h — высота. Решая эту формулу относительно h, вы получите высоту трапеции: h = 2S / (a + b).

Как рассчитать площадь криволинейной трапеции?

Чтобы рассчитать площадь криволинейной трапеции, необходимо знать длины ее оснований и наклонных боковых сторон, а также высоту. Затем вы можете использовать формулу для площади трапеции: S = (a + b)h/2, где a и b — длины оснований, h — высота. Для криволинейной трапеции вместо a и b необходимо использовать длины соответствующих наклонных сторон.

Как проверить, что я правильно рассчитал площадь трапеции?

Вы можете проверить правильность своих расчетов, используя формулу для площади трапеции. Также вы можете использовать наш онлайн калькулятор площади трапеции, чтобы проверить свои расчеты. Если вы измерили длины сторон и углы трапеции с помощью инструментов, то также можете проверить свои измерения, сравнив их с теоретическими значениями.

Можно ли рассчитать площадь трапеции, зная только диагонали?

Если вы знаете длины диагоналей трапеции и угол между ними, то можно использовать формулу для расчета площади трапеции: S = (1/2)d1d2sin(theta), где d1 и d2 — диагонали, а theta — угол между ними.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.

Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!

Есть что добавить?

Напишите своё мнение, комментарий или предложение.

Показать комментарии

Источник

Выберите подписку для получения дополнительных возможностей Kalk.Pro

Любая активная подписка отключает

рекламу на сайте

- Доступ к скрытым чертежам
- Безлимитные сохранения расчетов
- Доступ к скрытым чертежам
- Безлимитные сохранения расчетов
- Доступ к скрытым чертежам
- Безлимитные сохранения расчетов
- Доступ к скрытым чертежам
- Безлимитные сохранения расчетов

Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.

Подробнее с подписками можно ознакомиться здесь.

Источник

Трапеция – это четырехугольник, у которого две стороны параллельны друг другу. Высотой трапеции называют линию, перпендикулярную основаниями, для удобства ее часто проводят из тупого угла трапеции на большее основание. Средняя линия трапеции – это линия, которая параллельна основаниям, и разделяет боковые стороны ровно пополам. Среднюю линию трапеции можно найти средним арифметическим оснований – сложив их и разделив на два.

Площадь трапеции в самом простом виде – это произведение средней линии на высоту, или если раскрыть формулу средней линии, то произведение полусуммы оснований на высоту.

Доказательством этой формулы будет служить представление площади трапеции, как суммы площадей двух треугольников полученных при проведении диагонали.

Площади этих треугольников будут равны соответственно и (для того, чтобы нарисовать высоту во втором треугольнике, необходимо будет продлить основание b). Площадь трапеции будет равна сумме полученных выражений, где мы вынесем высоту за скобку, и получим искомую формулу:

Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с помощью метода подстановки.

Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y.
Таким образом x+y=d-b, y=d-b-x.
Одинаковый катет у обоих треугольников – высота, которую мы ищем. Через теорему Пифагора в прямоугольных треугольниках выражаем высоту и . Приравнивая, получаем a²-x²=c²-y² или x²-y²=a²-c².
x²-(d-b-x)²=a²-c² — Подставляем вместо х полученное выше выражение d-b-y.
x²-d²+bd+dx-b²+bd-bx-x²+dx-bx=a²-c² — Раскрываем скобки.
x²-d²+2bd+2dx-b²-2bx-x²=a²-c² — Приводим подобные слагаемые.
2dx-2bx=a²-c²+d²+b²-2bd — Переносим все вправо, оставляя слева только y.
2x(d-b)=a²-c²+(d-b)² — Выносим общие множители.

Подставляем обратно y в формулу высоты .
Формула площади трапеции через стороны будет выглядеть так:

Площадь трапеции через диагонали и угол между ними считается условным делением трапеции на четыре треугольника, точно также как и площадь любого произвольного четырехугольника.

Площадь равнобедренной трапеции можно найти еще одним способом, если даны угол при основании и радиус вписанной окружности. Дело в том, что центр вписанной окружности, откуда берет свое начало радиус, находится точно в центре трапеции, таким образом, приравнивая высоту и диаметр окружности (либо удвоенный радиус). Также одно из свойств трапеции, описанной вокруг окружности – это равенство суммы оснований и суммы боковых сторон, значит, мы сможем найти среднюю линию, зная боковые стороны. Проведя высоту, из прямоугольного треугольника получаем боковую сторону и среднюю линию
Тогда площадь трапеции равна

Источник