- Категория: Задачи по планиметрии
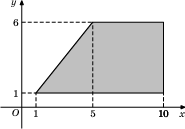
Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (10;6), (5;6).
Решение:
Ответ: 35.
Найдите площадь трапеции , вершины которой имеют координаты (1;0) , (1;8), (8;3), (8;7)
Площадь трапеции находится по формуле:
S = 1/2 * (а + b) * h, где а и b — параллельные основания, а h – высота трапеции.
Нарисуем трапецию:
https://bit.ly/2xMkEeW
На рисунке мы видим, что в качестве параллельных оснований выступают отрезки AB и CD, а в качестве высоты отрезок CE.
Перепишем формулу исходя из рисунка:
S = 1/2 * (AB + CD) * CE.
Исходя из рисунка, найдем длины отрезков AB, CD и CE:
AB = 8 -0 = 8;
CD = 7 -3 = 4;
CE = 8 -1 = 7.
Подставим найденные величины отрезков в нашу формулу:
S = 1/2 * (8 + 4) * 7 = 42
Ответ: площадь трапеции 42.
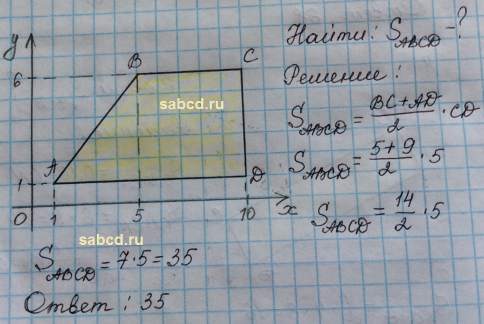
Площадь трапеции равна полусумме оснований, умноженной на высоту, то есть S = ½⋅(a+b)⋅h, где a,b — основания трапеции, h — высота трапеции.
В нашем случае: AD, BC — основания трапеции, BH — высота трапеции.
Найдем основание AD, оно равно разности координат по х:
AD = 10 — 1 = 9
Аналогичным образом найдем основание BC:
BC = 6 — 3 = 3
Найдем высоту BH:
BH = 7 — 1 = 6
В конечном счете получаем:
S = ½⋅(AD + BC)⋅BH
S = ½⋅(9 + 3)⋅6
S = ½⋅12⋅6
S = 6⋅6
S = 36
Ответ: 36
Рассмотрим задачу. Формула площади трапеции : S=1/2h(a+b) , где h — высота, а,b — основания трапеции.
Примерно представим,как выглядит на координатной прямой трапеция, где она расположена. Большее основание расположено так :(1;3), (10;3). Его длину можно вычислить , если рассматривать относительно оси Ох. Мысленно проведем перпендикуляры из этих точек на ось Ох, а теперь рассчитаем длину основания: а=10-1=9.( тк первая точка не выходит из координаты (0;0) или же (0;у), поэтому из большего мы вычитаем меньшее). Аналогично поступим с меньшим основанием, имеющем координаты (6:8), (3;8): b=6-3=3 . Теперь найдем высоту, для этого нам нужно опустить перпендикуляры из точек на ось Ок и вычислить разницу : h=8-3=5. Мы можем найти площадь трапеции:S=1/2h(a+b)=1/2*5*(3+9)= 30
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 10670 Найдите площадь прямоугольной трапеции,…
Условие
Julia_Trusova
20.10.2016
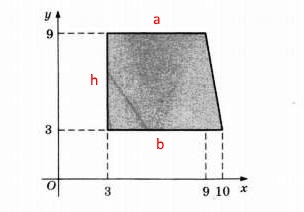
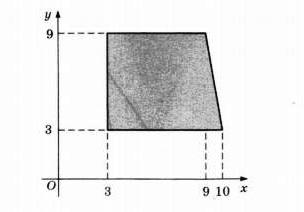
Найдите площадь прямоугольной трапеции, вершины которой имеют координаты (3;3); (10;3); (9;9); (3;9).
математика 10-11 класс
19983
Решение
Так как трапеция равнобедренная, то высотой будет являться боковая сторона, перпендикулярная основаниям.
a=9-3=6
b=10-3=7
h=9-3=6
S=1/2*(6+7)*6=39
Ответ: 39
Вопросы к решению (1)
Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач