{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения — зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу
mu = dfrac{F_{тр}}{mg}
Fтр — сила трения
m — масса тела
g — ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона
mu = tg(alpha)
α — угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
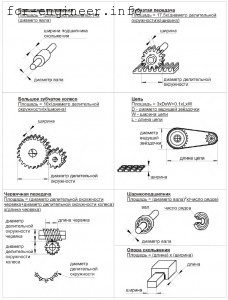
Расчет площади поверхности трения
Площади поверхностей семи основных типов точек смазки рассчитываются по следующим формулам (размерность в см2)
В соответствии с конструкцией узла смазки необходимо выбрать подходящую формулу из представленных выше для своего случая. Вычислить площадь поверхности (в см2) для каждой точки смазки (округлять в сторону ближайшего целого числа).
Площадь — трение
Cтраница 1
Площадь трения этих пружин около 2×5 мм. Якорь и контактная система реле собраны на отдельном керамическом основа-нии.
[2]
Этот коэффициент представляет собой отношение площадей трения трущихся элементов. Большое влияние этого показателя на трение объясняется тем, что от его значения существенно зависит тепловой режим, напряженное состояние и возможность попадания окружающей среды на поверхность трения. Неполное взаимное перекрытие обеспечивает возможность теплоотдачи с открытых участков поверхности трения; при полном перекрытии все тепло идет в глубь трущихся тел. Поэтому с уменьшением взаимного перекрытия имеется тенденция [35] к снижению поверхностной температуры и росту температурного градиента д & / дг.
[3]
Этот коэффициент представляет собой отношение площадей трения трущихся элементов. Большое влияние этого показателя на трение объясняется тем, что от его значения существенно зависят тепловой режим, напряженное состояние и возможность попадания окружающей среды на поверхность трения. Неполное взаимное перекрытие обеспечивает возможность теплоотдачи с открытых участков поверхности трения; при полном перекрытии вся теплота идет в глубь трущихся тел.
[4]
Это объясняется тем, что соотношение площадей трения асбофрикционного образца и контрэлемента становится настолько малым, что образующихся смазочных продуктов деструкции оказывается недостаточно для осуществления эффективного смазывающего действия.
[6]
Для правильного выбора конструкции и размеров площадей трения колодочных тормозов необходимо знать законы распределения удельного давления на поверхности трения.
[8]
Па — с; / 2 — площадь трения, м2; dwldl — градиент скорости ( вследствие трения возникает разность скоростей перпендикулярно к направлению потока); dl — расстояние между движущимися слоями жидкости.
[9]
Что касается числа лопастей, то для уменьшения площади трения и упрощения технологии производства целесообразно было бы применять рабочие колеса с минимальным количеством лопастей. Однако энергетические условия работы лопастей при этом ухудшаются. Практически стремятся к наименьшему числу лопастей рабочего колеса, однако при условии, что снижение числа лопастей не приводит к потере их направляющего действия.
[10]
Диаметр ролика 30 мм, ширина 10 мм, площадь трения 1 см2, колодка из закаленной стали 45, трение без смазки при 425 об / мин в течение 1000 оборотов.
[11]
Цилиндровое масло должно хорошо распыливатьея, равномерно распределяться по площадям трения и не образовывать нагара, что обусловливается стойкостью масла против окисления кислородом воздуха при высоких температурах. Масло не должно также вызывать коррозии металлических поверхностей; должно сохранять необходимую текучесть при низких температурах.
[12]
Цилиндровое масло должно хорошо распыливаться, равномерно распределяться по площадям трения и не должно образовывать нагара, что обуславливается стойкостью масла против окисления кислородом воздуха при высоких температурах. Масло не должно вызывать коррозии металлических поверхностей; нужно также, чтобы оно сохраняло необходимую текучесть при низких температурах. Цилиндровые масла делят на две основные группы: для машин, работающих насыщенным паром; для машин, работающих перегретым паром.
[13]
Лучшими показателями по прочности масляной пленки, наибольшему допустимому давлению на площадь трения и износу трущихся деталей машины обладает масло 2, содержащее взвешенные углеродистые вещества.
[14]
При этом под тепловым потоком понимается количество тепла, приходящееся на единицу площади трения в единицу времени.
[15]
Страницы:
1
2
3
4
5
Большое трение. Что такое трение в физике? Польза и вред силы трения
Как найти площадь фигуры?
Знать и уметь рассчитывать площади различных фигур необходимо не только для решения простых геометрических задач. Не обойтись без этих знаний и при составлении или проверке смет на ремонт помещений, расчета количества необходимых расходных материалов. Поэтому давайте разберемся, как находить площади разных фигур.
Часть плоскости, заключенная внутри замкнутого контура, называется площадью этой плоскости. Выражается площадь количеством заключенных в ней квадратных единиц.
Чтобы вычислить площадь основных геометрических фигур, необходимо использовать правильную формулу.
Площадь треугольника
Обозначения:
- Если известны h, a, то площадь искомого треугольника определяется как произведение длин стороны и высоты треугольника, опущенной к этой стороне, разделенное пополам: S=(a·h)/2
- Если известны a, b, c, то искомая площадь рассчитывается по формуле Герона: корень квадратный, взятый из произведения половины периметра треугольника и трех разностей половины периметра и каждой стороны треугольника: S = √(p·(p — a)·(p — b)·(p — c)).
- Если известны a, b, γ, то площадь треугольника определяется как половина произведения 2-х сторон, умноженная на значение синуса угла между этими сторонами: S=(a·b·sin γ)/2
- Если известны a, b, c, R, то искомая площадь определяется как деление произведения длин всех сторон треугольника на четыре радиуса описанной окружности: S=(a·b·c)/4R
- Если известны p, r, то искомая площадь треугольника определяется умножением половины периметра на радиус вписанной в него окружности: S=p·r
Площадь квадрата
Обозначения:
- Если известна сторона, то площадь данной фигуры определяется как квадрат длины его стороны: S=a 2
- Если известна d, то площадь квадрата определяется как половина квадрата длины его диагонали: S=d 2 /2
Площадь прямоугольника
Обозначения:
- S — определяемая площадь,
- a, b — длины сторон прямоугольника.
- Если известны a, b, то площадь данного прямоугольника определяется произведением длин двух его сторон: S=a·b
- Если длины сторон неизвестны, то площадь прямоугольника нужно разбить на треугольники. В этом случае площадь прямоугольника определяется как сумма площадей составляющих его треугольников.
Площадь параллелограмма
Обозначения:
- S — искомая площадь,
- a, b — длины сторон,
- h — длина высоты данного параллелограмма,
- d1, d2 — длины двух диагоналей,
- α — угол, находящийся между сторонами,
- γ — угол, находящийся между диагоналями.
- Если известны a, h, то искомая площадь определяется перемножением длин стороны и высоты, опущенной на эту сторону: S=a·h
- Если известны a, b, α, то площадь параллелограмма определяется перемножением длин сторон параллелограмма и значения синуса угла между этими сторонами: S=a·b·sin α
- Если известны d 1 , d 2 , γ то площадь параллелограмма определяется как половина произведения длин диагоналей и значения синуса угла между этими диагоналями: S=(d 1 ·d 2 ·sinγ)/2
Площадь ромба
Обозначения:
- S — искомая площадь,
- a — длина стороны,
- h — длина высоты,
- α — меньший угол между двумя сторонами,
- d1, d2 — длины двух диагоналей.
- Если известны a, h, то площадь ромба определяется умножением длины стороны на длину высоты, которая опущена на эту сторону: S=a·h
- Если известны a, α, то площадь ромба определяется перемножением квадрата длины стороны на синус угла между сторонами: S=a 2 ·sin α
- Если известны d 1 и d 2 , то искомая площадь определяется как половина произведения длин диагоналей ромба: S=(d 1 ·d 2)/2
Площадь трапеции
Обозначения:
- Если известны a, b, c, d, то искомая площадь определяется по формуле: S= (a+b) /2 *√ .
- При известных a, b, h, искомая площадь определяется как произведение половины суммы оснований и высоты трапеции: S=(a+b)/2·h
Площадь выпуклого четырехугольника
Обозначения:
- Если известны d 1 , d 2 , α, то площадь выпуклого четырехугольника определяется как половина произведения диагоналей четырехугольника, умноженная на величину синуса угла между этими диагоналями: S=(d 1 · d 2 ·sin α)/2
- При известных p, r площадь выпуклого четырехугольника определяется как произведение полупериметра четырехугольника на радиус окружности, вписанной в этот четырехугольник: S=p·r
- Если известны a, b, c, d, θ, то площадь выпуклого четырехугольника определяется как корень квадратный из произведений разницы полупериметра и длины каждой стороны за минусом произведения длин всех сторон и квадрата косинуса половины суммы двух противоположных углов: S 2 = (p — a)(p — b)(p — c)(p — d) — abcd·cos 2 ((α+β)/2)
Площадь круга
Обозначения:
Если известен r, то искомая площадь определяется как произведение числа π на радиус в квадрате: S=π r 2
Если известна d, то площадь круга определяется как произведение числа π на квадрат диаметра, поделенное на четыре: S=(π·d 2)/4
Площадь сложной фигуры
Сложную можно разбить на простые геометрические фигуры. Площадь сложной фигуры определяется как сумма или разность составляющих площадей. Рассмотрим, к примеру, кольцо.
Обозначение:
- S — площадь кольца,
- R, r — радиусы внешней окружности и внутренней соответственно,
- D, d — диаметры внешней окружности и внутренней соответственно.
Для того чтобы найти площадь кольца, надо из площади большего круга отнять площадь 
меньшего круга. S = S1-S2 = πR 2 -πr 2 = π (R 2 -r 2).
Таким образом, если известны R и r, то площадь кольца определяется как разница квадратов радиусов внешней и внутренней окружностей, умноженная на число пи: S=π(R 2 -r 2).
Если известны D и d, то площадь кольца определяется как четверть разницы квадратов диаметров внешней и внутренней окружностей, умноженная на число пи: S= (1/4)(D 2 -d 2) π.
Площадь закрашенной фигуры
Предположим, что внутри одного квадрата (А) находится другой (Б) (меньшего размера), и нам нужно найти закрашенную полость между фигурами «А» и «Б». Скажем так, «рамку» маленького квадрата. Для этого:
- Находим площадь фигуры «А» (вычисляется по формуле нахождения площади квадрата).
- Аналогичным образом находим площадь фигуры «Б».
- Вычитаем из площади «А» площадь «Б». И таким образом получаем площадь закрашенной фигуры.
Теперь вы знаете, как находить площади разных фигур.
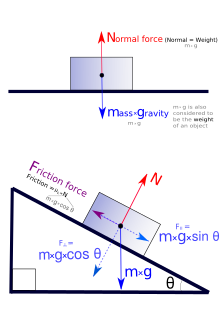
Изображения сил действующих на скользящее тело.
Изображения действующих сил на тело, находящееся на ровной и наклонной плоскости.
Сила трения скольжения — сила, возникающая между соприкасающимися телами при их относительном движении.
Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения. Так как никакое тело не является абсолютно ровным, сила трения не зависит от площади соприкосновения, и истинная площадь соприкосновения гораздо меньше наблюдаемой; кроме того, увеличивая площадь, мы уменьшаем удельное давление тел друг на друга[1].
Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается латинской буквой 
или греческой буквой 
. Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то можно считать постоянным. В первом приближении величина силы трения скольжения может быть рассчитана по формуле[1]:
— коэффициент трения скольжения,
— сила нормальной реакции опоры.
Силами трения называются тангенциальные взаимодействия между соприкасающимися телами, возникающие при их относительном перемещении.
Опыты с движением различных соприкасающихся тел (твёрдых по твёрдым, твёрдых в жидкости или газе, жидких в газе и т. п.) с различным состоянием поверхностей соприкосновения показывают, что силы трения проявляются при относительном перемещении соприкасающихся тел и направлены против вектора относительной скорости тангенциально к поверхности соприкосновения. При этом всегда в большей или меньшей степени происходит преобразование механического движения в другие формы движения материи — чаще всего в тепловую форму движения, и происходит нагревание взаимодействующих тел.
Типы трения скольжения
Если между телами отсутствует жидкая или газообразная прослойка (смазочный материал), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.
По физике взаимодействия трение скольжения принято разделять на:
- Сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазочными материалами — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя.
- Сухое с сухой смазкой (графитовым порошком)
- Жидкостное, при взаимодействии тел, разделённых слоем жидкости или газа (смазочного материала) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость;
- Смешанное, когда область контакта содержит участки сухого и жидкостного трения;
- Граничное, когда в области контакта могут содержаться слои и участки различной природы (окисные плёнки, жидкость и т. д.) — наиболее распространённый случай при трении скольжения.
Также можно классифицировать трение по его области. Силы трения, возникающие при относительном перемещении различных тел, называются силами внешнего трения. Силы трения возникают и при относительном перемещении частей одного и того же тела. Трение между слоями одного и того же тела называется внутренним трением.
Измерение
В связи со сложностью физико-химических процессов, протекающих в зоне фрикционного взаимодействия, процессы трения принципиально не поддаются описанию с помощью методов классической механики. Поэтому нет точной формулы для коэффициента трения. Его оценка производится на основе эмпирических данных: так как по первому закону Ньютона тело движется равномерно и прямолинейно, когда внешняя сила уравновешивает возникающую при движении силу трения, то для измерения действующей на тело силы трения достаточно измерить силу, которую необходимо приложить к телу, чтобы оно двигалось без ускорения.
Таблица коэффициентов трения скольжения
Значения таблицы взяты из справочника по физике[2]
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,028 | |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь (коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примечания
- ↑ 1 2 Билимович Б. Ф. Законы механики в технике. — М., Просвещение, 1975. — Тираж 80000 экз. — с. 58
- ↑ Енохович А. С. Справочник по физике. — Просвещение, 1978. — С. 85. — 416 с.