Формулы площадей всех основных фигур
1. Формула площади круга через радиус или диаметр
Зная диаметр или радиус круга, можно найти его площадь.
r — радиус круга
D — диаметр
Формула площади круга, (S):
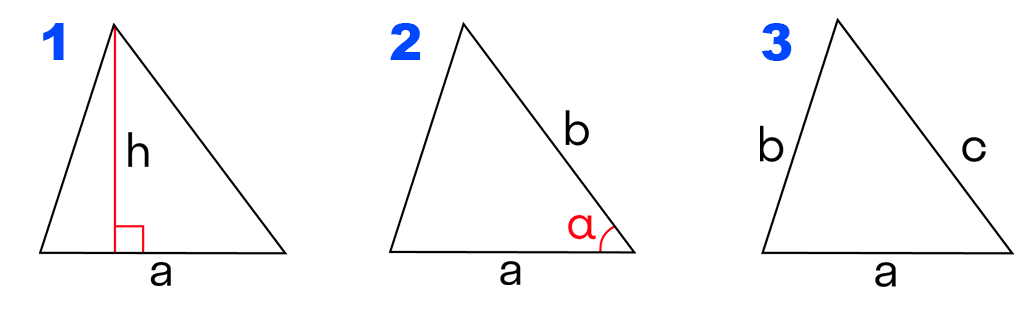
2. Формула расчета площади треугольника
h — высота треугольника
a — основание
Площадь треугольника (S):
3. Площадь треугольника, формула Герона
a , b , c , — стороны треугольника
p— полупериметр, p=( a + b + c )/2
Формула ( Герона ) площади треугольника через полупериметр ( S ):
4. Площадь прямоугольного треугольника по катетам
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.
a , b — катеты треугольника
Формула площади прямоугольного треугольника, (S):
5. Как вычислить площадь равнобедренного треугольника ?
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b , ( S ):
Формула площади треугольника через, стороны a , b , (S):
6. Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h — высота
Площадь треугольника только через сторону a , (S):
Площадь треугольника только через высоту h , ( S ):
Площадь треугольника через сторону a и высоту h , (S):
7. Найти площадь треугольника, угол и две стороны
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.
a , b , c — стороны треугольника
α , β , γ — углы
Формулы площади треугольника, через две стороны и угол между ними, ( S ):
8. Площадь треугольника по стороне и двум углам, формула.
a , b , c — стороны треугольника
α , β , γ — противолежащие углы
Площадь треугольника через сторону и два угла (S):
9. Формула расчета площади прямоугольника
b — длина прямоугольника
a — ширина
Формула площади прямоугольника, (S):
10. Как рассчитать площадь квадрата через диагональ или сторону
a — сторона квадрата
c — диагональ
Формула площади квадрата через сторону a , (S):
Формула площади квадрата через диагональ c , (S):
11. Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α , β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, ( S ):
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
H b — высота на сторону b
H a — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d — меньшая диагональ
α , β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
12. Площадь произвольной трапеции
1. Формула площади трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
m — средняя линия
h — высота трапеции
Формула площади трапеции, (S):
2. Формула площади трапеции через диагонали и угол между ними
d 1, d 2 — диагонали трапеции
α , β — углы между диагоналями
Формула площади трапеции, (S):
3. Формула площади трапеции через четыре стороны
b — верхнее основание
a — нижнее основание
c, d — боковые стороны
Формула площади трапеции, (S):
13. Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α , β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α , β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α , β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Треугольник вписанный в окружность
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = frac<1><2>ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
http://www.mozgan.ru/Geometry/AreaTriangle
http://colibrus.ru/treugolnik-vpisannyy-v-okruzhnost/
Фигура с 3 отрезками в геометрии определяется, как треугольник. Равносторонний тот, у которого все
стороны имеют одинаковый размер.
Чтобы произвести измерения площади геометрической фигуры, специалисты применяют универсальную
формулу, которая выглядит следующим образом: S = 1/2 * ah, где S — площадь фигуры, а — длина (чтобы
узнать величину, необходимо измерить расстояние от А до В, h — высота. Для определения переменной
необходимо провести медиану. Ее размер и будет высотой.
Также определить параметры равносторонней
фигуры можно другими способами: через радиус и диаметр вписанной и описанной окружности, площадь
описанного и вписанного круга, периметр описанной и вписанной окружности, сторону, высоту.
- Площадь равностороннего треугольника через радиус описанной
окружности - Площадь равностороннего треугольника через диаметр
описанной окружности - Площадь равностороннего треугольника через площадь
описанного круга - Площадь равностороннего треугольника через длину описанной
окружности (периметр) - Площадь равностороннего треугольника через радиус вписанной
окружности - Площадь равностороннего треугольника через диаметр
вписанной окружности - Площадь равностороннего треугольника через площадь
вписанного круга - Площадь равностороннего треугольника через длину вписанной
окружности (периметр) - Площадь равностороннего треугольника через сторону
- Площадь равностороннего треугольника через высоту
Через радиус описанной окружности
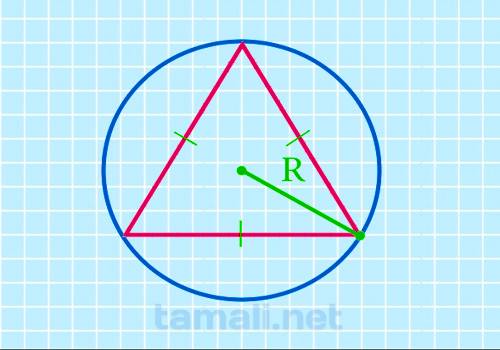
Треугольник может иметь лишь 1 описанную окружность. Для этого три отрезка геометрической фигуры
должны быть внутри круга. Зная радиус, который относится, к описанной окружности, можно применить
эту формулу для выполнения расчетов:
S = 3*√3 / 4*R²
где S — площадь фигуры, R — радиус описанной окружности.
Цифр после
запятой:
Результат в:
Это размеры отрезка от центра круга до любой вершины. Например, если R=5 см, то определение размеров
будет выполняться следующим образом:
S = 3√3/4*5²=3*1.732/4*25 = 32.476 м². Таким образом, применив формулу,
можно узнать искомую величину.
Через диаметр описанной окружности
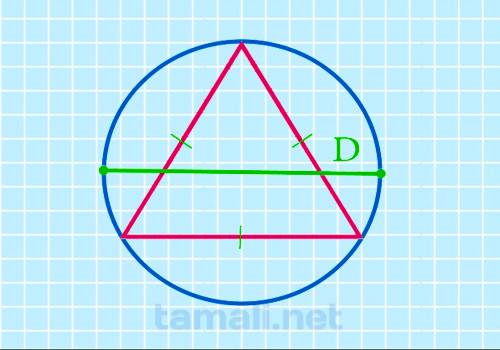
Под диаметром понимается отрезок, проходящий через центр окружности, а также соединяющий две точки.
Другими словами, длина упомянутой линии и будет значением диаметра. Если значение диаметра
неизвестно, но известен радиус, переменную можно рассчитать с помощью данного метода: D=2R, где R —
радиус, D — диаметр. Определив диаметр описанной фигуры, можно применить такую формулу для
расчетов:
S = 3 * √3 / 16 * D²
где S — площадь фигуры, D — диаметр описанного круга.
Цифр после
запятой:
Результат в:
То есть, длина луча, который начинается от 1 стороны круга. Также он проходит через центр окружности
и описанного геометрического объекта. Завершается отрезок на противоположной части круга. К примеру,
если D=6 м, то расчет размеров будет выполняться следующим образом: S = 3√3/16*6²=3*1.732/16*36 = 11.691 м²
Применив эту формулу, можно найти искомую величину.
Через площадь описанного круга
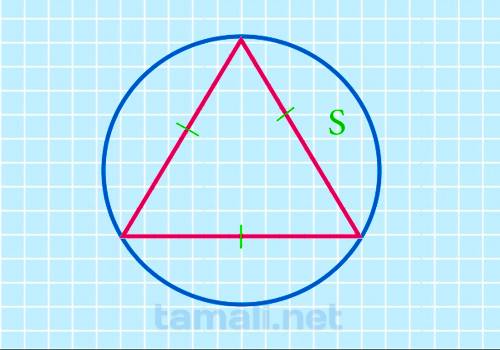
После того, как размеры круга станут известны, можно найти с помощью них площадь геометрической
фигуры. Для этого необходимо воспользоваться математической формулой:
S1 = 3 * √3 / 4 * π * S2
где S1 — площадь треугольника, S2 — площадь круга.
Цифр после
запятой:
Результат в:
Для вычисления потребуется знать радиус окружности, чтобы с помощью него определить размеры круга.
Она рассчитывается по данной формуле: S = π * R², где R — радиус, π — число Пи, значение величины
всегда остается неизменным и равно 3,1415926535. На практике расчет переменной круга проще показать
на конкретной задаче. Например, если R=5, π = 3,14, то следовательно S = 3,14*25 = 78,5
К примеру, если S2= 78,5, то расчет размеров будет выполняться следующим образом: S = 3 * √3 / 4π
*78,5=3*1.732/4π*78,5 = 32.459 м². Используя такой метод можно определить S равностороннего
объекта.
Через радиус вписанной окружности
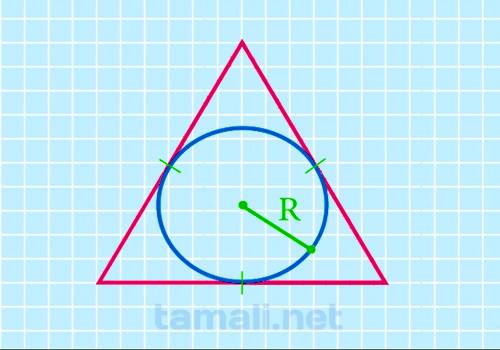
У треугольника может быть только одна вписанная окружность. Для этого круг должен быть внутри фигуры,
а также соприкасаться со всеми ее сторонами. Если указан радиус, который относится, к вписанной
окружности, можно использовать эту формулу для определения общих размеров искомой фигуры:
S = 3 * √3 * R² где S — площадь геометрической фигуры, R — радиус вписанного круга. Это длина
прямой от центра круга до любой стороны.
Цифр после
запятой:
Результат в:
К примеру, если R=5, то расчет будет осуществляться так: S = 3√3*5²=3*1.732*25 = 129.903 м². Таким
образом, следуя данной формуле, можно решить задачу.
Через длину описанной окружности (периметр)
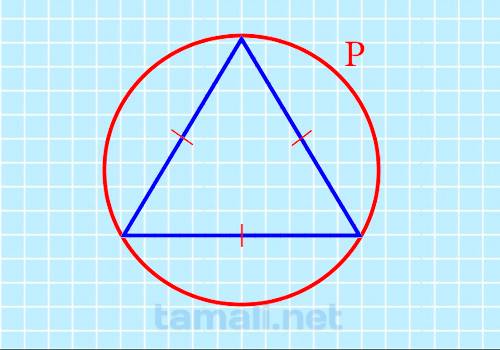
После того, как периметр круга будет подсчитан, можно определить с помощью него площадь
геометрического объекта. Для этого необходимо подставить полученное значение в формулу:
S = 3√3/16π² * P² где S — площадь треугольника, P — периметр или длина круга.
Цифр после
запятой:
Результат в:
Длина, а также периметр описанной окружности определяются как луч, охватывающий геометрическую фигуру
в 2 измерениях. Периметр рассчитывается по такой формуле: S = 2πR где R — радиус, π — число Пи.
Значение величины считается постоянным и равно 3,1415926535.
На практике расчет длины круга легче продемонстрировать на определенной задаче. Например, если R=5, π
= 3,14, то следовательно Р круга = 2 * 3,14 * 5 = 31,4. К примеру, если P= 31,4, то расчет
размеров будет производиться следующим образом: S = 3 * √3 / 16 π² * 31,4²=3 * 1.732 / 16 * 9,85 =
32.443 м². С помощью такой схемы можно рассчитать S искомой фигуры.
Через диаметр вписанной окружности
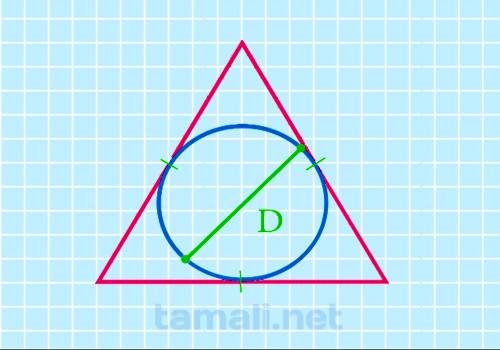
Зная диаметр вписанной окружности, рекомендуется использовать такую формулу для определения
площади:
S = 3 * √3 / 4 * D²
где S — площадь геометрической фигуры, D — диаметр вписанной окружности.
Цифр после
запятой:
Результат в:
Диаметр в геометрии определяется, как луч, который проходит через центр окружности и соединяет две
точки. Если сказать проще, то длина упомянутой линии и будет значением диаметра. В ситуации, когда
известен радиус, но нет данных о диаметре, необходимо рассчитать его с помощью этой формулы: D=2R, где R — радиус, D — диаметр. То есть, длина отрезка, который
начинается от стороны круга, а также пересекает центр и заканчивается на противоположной стороне.
К примеру, если D=6, то расчет размеров производится, как на представленном примере: S = 3 * √3 / 4 * 6²=3 * 1.732 / 4 * 36 = 32.475 м².
Через длину вписанной окружности (периметр)
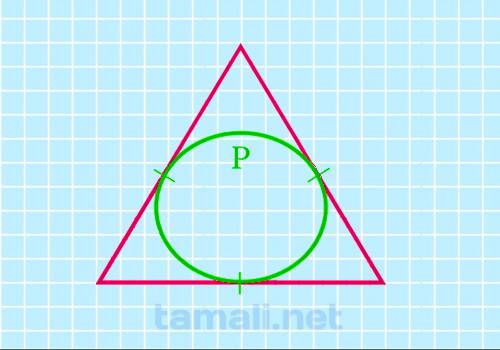
После нахождения значения периметра, можно определить с помощью него параметры требуемого объекта.
Для этого потребуется подставить полученное число в формулу:
S = 3√3/4π*P²
где S — площадь треугольника, P — длина вписанной окружности.
Цифр после
запятой:
Результат в:
Длина или периметр окружности определяются как луч, охватывающий геометрическую фигуру в 2
измерениях. Периметр рассчитывается по формуле: S = 2πR, где R — радиус, π
— число Пи. Значение величины считается постоянным и равно 3,1415926535. Чтобы было нагляднее, длину
круга легче продемонстрировать на конкретной задаче. Например, если R=5, π = 3,14, то следовательно
P круга = 2* 3,14*5 = 31,4.
К примеру, если P= 31,4, то расчет размеров будет производиться следующим образом: S = 3√3/4π*31,4²=3*1.732/4*3.14*985 = 407,691 м². С помощью такого
способа можно рассчитать S искомой фигуры.
Через сторону
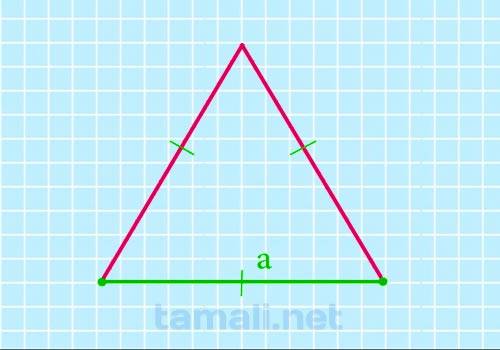
Все отрезки у этого геометрического объекта равны между собой. Поэтому, достаточно знать длину
любого. Определив сторону фигуры, можно применить следующую формулу для расчета размеров:
S = √3/4a²
где S — площадь геометрического объекта, a — длина отрезка.
Цифр после
запятой:
Результат в:
К примеру, если a =5, то расчет размеров будет выполняться следующим образом: S = √3/4*5²=3*1.732/4*25 = 10.825 м².
Через высоту
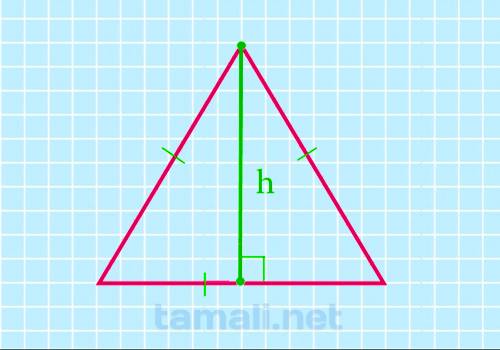
Медиана в такой фигуре является высотой и биссектрисой. По этой причине достаточно провести медиану,
чтобы узнать высоту объекта. Зная высоту, можно применить следующую формулу для расчета:
S = h²/√3
где S — площадь, h — высота.
Цифр после
запятой:
Результат в:
Например, если h =5, то расчет S будет осуществляться следующим способом: S = 5²/√3=25/1.732 = 14.433 м².
С помощью этой формулы можно узнать общие размеры равностороннего треугольника.
Через площадь вписанного круга
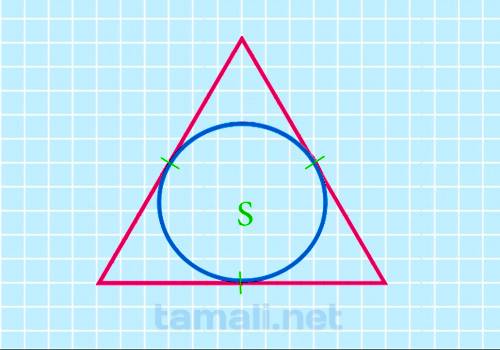
После того, как переменные круга найдены, предстоит вычислить с помощью них S фигуры. Для этого
потребуется применить формулу:
S1 = 3*√3/π*S2
где S1 — площадь треугольника, S2 — площадь вписанного круга.
Цифр после
запятой:
Результат в:
Для вычисления потребуется знать радиус окружности, чтобы с помощью него определить общие размеры
круга. Чтобы их рассчитать потребуется данная формула: S= π*R², где R —
радиус, π — число Пи. Константа, которая всегда равна 3,1415926535. На практике расчет площади круга
нагляднее продемонстрировать на конкретном упражнении. Например, если R=6, π = 3,14, то
следовательно S круга = 3,14*36 = 113
К примеру, если S2= 113, то расчеты будут выглядеть следующим образом: S = 3√3/π*113=3*1.732/π*113 = 186,900 м²
Практическое применение формулы для определения площади равностороннего треугольника
Чтобы было проще понять, рекомендуется начертить на листе бумаге объект с 3 равными отрезками. У него
необходимо обозначить каждую сторону латинскими буквами, например, «А» «B» «C». В результате должна
получиться фигура, у которой стороны АВ=ВС=АС.
Треугольник, который имеет стороны одного размера, обладает следующими есть свойствами:
- Все углы между собой равны. ∠А=∠B=∠C. Из курса геометрии известно, что у данной фигуры сумма
углов составляет 180°. Следовательно, = 60°. - Медиана считается биссектрисой, а также высотой. Медиана — линия, которая соединяет вершину
треугольника с противоположным отрезком. Биссектриса — отрезок, разделяющий угол пополам.
Правильно рассчитать размеры геометрической фигуры полезно не только для сдачи экзаменов, но и в
повседневной жизни. Например, есть задача — оформить грядку. Для нее потребуется земля. Чтобы
понимать, сколько купить материала, необходимо знать размеры участка. Если объект прямоугольной
формы все просто — достаточно умножить длину на ширину. Однако, в случае с треугольниками придется
использовать другую формулу.
Кроме того, необходимо понимать, какой тип фигуры представлен в задаче: равнобедренный или
равносторонний.
Таким образом, понимая, как правильно вычислить S геометрической фигуры с 3 сторонами, можно легко
решить задачу по геометрии или применить знания в реальной жизни.
Важно учитывать, что вышеперечисленные формулы подходят для вычисления размеров именно
равностороннего треугольника. К примеру, чтобы определить площадь прямоугольного треугольника
потребуется знать длину стороны «а» и «b», поскольку у них разное значение. Также необходимо
измерить или найти гипотенузу прямоугольной геометрической фигуры.
Умение вычисления S геометрического объекта по формуле будет полезно при выполнении математических
упражнений. Кроме того, такие знания пригодятся в реальной жизни, когда потребуется измерить размеры
объекта треугольной формы. Например, при копании грядок на огороде или для проведения строительных
работ по возведению здания в виде пирамиды.
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
📐 Когда нужно знать площадь треугольника?
Знание площади треугольника может быть полезно во многих сферах жизни, включая математику, науки, строительство, дизайн и другие области.
Вот некоторые конкретные примеры, когда необходимо знать площадь треугольника:
- В математике – для решения задач на нахождение площади треугольника или расчета других параметров на основе площади.
- В науках – для расчета площади треугольной формы в различных контекстах, например, при изучении геометрии или физики.
- В строительстве – для расчета площади треугольного участка поверхности, например, для закупки материалов или расчета стоимости работ.
- В дизайне – для расчета площади треугольных участков земли или других поверхностей, например, для планировки ландшафта или выбора размера ковра.
- В повседневной жизни – для решения различных задач, например, для расчета площади треугольной поверхности мебели или для оценки площади треугольного участка земли в саду.
Знание площади треугольника может быть полезным во многих ситуациях, где треугольная форма играет важную роль, и поможет справиться с различными задачами более эффективно.
Как рассчитывается площадь треугольника?
Площадь треугольника может быть рассчитана на основе формулы, зависящей от известных параметров треугольника. Существуют несколько различных формул для расчета площади треугольника, которые можно использовать в зависимости от того, какие параметры известны.
Формула 1. Через длину основания и высоту, опущенную на это основание:
S = a × h/2
Формула 2. Через две стороны и угол между ними:
S = 1/2 × a × b × sin α
где α — угол между сторонами а и b
Формула 3. Формула Герона через 3 стороны:
S = √ [p × (p-a) × (p-b) × (p-c)]
где p = (a+b+c)/2 – полупериметр.
Во всех формулах S обозначает площадь треугольника, b обозначает длину основания прямоугольного треугольника, h обозначает высоту, a, b, и c обозначают длины сторон непрямоугольного треугольника, x и y обозначают координаты вершин треугольника.
Рассчитывая площадь треугольника, важно использовать правильную формулу в зависимости от известных параметров, чтобы получить правильный ответ.
Что такое калькулятор площади треугольника?
Калькулятор площади треугольника – это онлайн-инструмент, который позволяет быстро и легко рассчитать площадь треугольника на основе известных параметров. Обычно для расчета площади треугольника в калькуляторе необходимо ввести значения одного или нескольких параметров, таких как длина основания и высота прямоугольного треугольника, длины всех трех сторон непрямоугольного треугольника или координаты вершин треугольника на координатной плоскости.
Калькулятор площади треугольника может быть полезен во многих ситуациях, например, при проектировании строительных конструкций, расчете площадей полей и участков земли, а также при решении математических задач в школе или вузе. Благодаря калькулятору площади треугольника можно быстро получить точный результат, избегая ошибок, которые могут возникнуть при ручных расчетах.
Как работает калькулятор площади треугольника?
Работа калькулятора площади треугольника может немного отличаться в зависимости от конкретного онлайн-инструмента, но обычно он использует формулу для расчета площади треугольника на основе заданных параметров.
Если треугольник является прямоугольным, то для расчета его площади необходимо знать длину основания и высоту, которая опускается на это основание. А если треугольник непрямоугольный, то для расчета его площади необходимо знать длины всех трех сторон.
Калькулятор площади треугольника может использовать эти формулы для расчета площади, если пользователь введет необходимые параметры (например, длины сторон или длину основания и высоту). Результат может быть выдан в виде числа или дроби в зависимости от точности калькулятора.
Как использовать калькулятор?
Использовать калькулятор площади треугольника довольно просто. Вот общие шаги, которые необходимо выполнить для использования калькулятора:
- Откройте калькулятор площади треугольника в своем браузере. Вы можете найти онлайн-калькуляторы площади треугольника на многих сайтах, которые предоставляют подобные сервисы, в том числе и на нашем.
- Введите параметры треугольника, которые известны вам. В зависимости от конкретного калькулятора вы можете вводить длины сторон, длину основания и высоту, координаты вершин на плоскости и т.д.
- Нажмите на кнопку «Рассчитать» или «Вычислить». Калькулятор площади треугольника обычно автоматически рассчитывает площадь на основе введенных параметров и выдает результат.
- Прочитайте результат. Калькулятор площади треугольника может выдавать результат в разных форматах, например, в виде числа или дроби. Если вы хотите, чтобы результат был точнее, можете использовать калькулятор с более высокой точностью.
- Сбросьте введенные данные и повторите расчет, если нужно. Если вам нужно рассчитать площадь треугольника с другими параметрами, то можете сбросить предыдущие данные и ввести новые параметры.
В целом, использование калькулятора площади треугольника довольно просто и позволяет быстро и точно рассчитать площадь треугольника на основе его параметров.
❓Вопросы и ответы
Также полезно ознакомиться с ответами на часто задаваемые вопросы по данному вопросу.
Как использовать калькулятор площади треугольника?
Для использования калькулятора площади треугольника нужно ввести известные параметры треугольника, такие как длины сторон, длина основания и высота, координаты вершин на плоскости и т.д., а затем нажать на кнопку «Рассчитать» или «Вычислить». Калькулятор автоматически рассчитывает площадь треугольника и выводит результат.
Какой формулой рассчитывается площадь треугольника?
Площадь треугольника можно рассчитать с помощью формулы: S = (a * h) / 2, где S – площадь треугольника, a – длина основания, h – высота, опущенная на основание.
Где можно найти онлайн-калькулятор площади треугольника?
Онлайн-калькуляторы площади треугольника можно найти на многих сайтах, которые предоставляют подобные сервисы. Также можно использовать калькуляторы научных порталов или мобильные приложения.
Какие единицы измерения используются в калькуляторе площади треугольника?
Калькулятор площади треугольника может использовать разные единицы измерения, например, метры, сантиметры, дюймы, футы и т.д. Обычно единицы измерения выбираются в соответствии с системой измерений, используемой в конкретной стране или регионе.
Можно ли использовать калькулятор площади треугольника для расчета площади других фигур?
Нет, калькулятор площади треугольника предназначен только для расчета площади треугольников. Для расчета площади других геометрических фигур необходимо использовать другие калькуляторы, например, калькуляторы площади круга, прямоугольника и т.д.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
— полупериметр треугольника; a,b,c — стороны треугольника.
Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:
a — основание треугольника; h — высота треугольника.
Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:
a,b — стороны треугольника; α — угол между сторонами.
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a— сторона треугольника; α и β — прилежащие углы.
Площадь прямоугольного треугольника

Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b — катеты треугольника.
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b — стороны треугольника.
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:
a — основание равнобедренного треугольника; α — угол между сторонами.
Площадь равностороннего треугольника через стороны

Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a — сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:
h — высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r — радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r — радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c — стороны треугольника; r — радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p — полупериметр треугольника;a, b, c — стороны треугольника; r — радиус вписанной окружности треугольника.
Содержание:
- Формула
- Примеры вычисления площади равностороннего треугольника
Формула
Чтобы найти площадь равностороннего треугольника (рис. 1), нужно квадрат его стороны умножить на
$sqrt{3}$ и поделить на четыре, то есть
$$mathrm{S}_{Delta}=frac{a^{2} sqrt{3}}{4}$$
Эту формулу легко получить из общей
формулы для площади треугольника
$$mathrm{S}_{Delta A B C}=frac{1}{2} a b sin alpha$$
при условии, что $a=b$ (так как треугольник равносторонний) и
$alpha=60^{circ}$ (угол равностороннего треугольника).
Напомним, что треугольник называется равносторонним, если все его стороны равны.
Примеры вычисления площади равностороннего треугольника
Пример
Задание. Найти площадь равностороннего треугольника
$ABC$, если известно, что его сторона равна 2 дм.
Решение. Подставив заданное значение в формулу, будем иметь:
$mathrm{S}_{Delta A B C}=frac{2^{2} cdot sqrt{3}}{4}=frac{4 cdot sqrt{3}}{4}=sqrt{3}$ (дм2)
Ответ. $mathrm{S}_{Delta A B C}=sqrt{3}$ (дм2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти площадь равностороннего треугольника
$ABC$, если его высота равна 3 м.
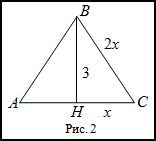
Решение. Сделаем чертеж (рис. 2).
Так треугольник равносторонний, то его высота $BH$ является и
медианой, а это означает, что $AH=HC$ .
Пусть $HC=x$, тогда $AC=2HC=2x=BC$. Рассмотрим прямоугольный треугольник
$BHC$. Записываем для него теорему Пифагора:
$$B C^{2}=B H^{2}+H C^{2}$$
$$(2 x)^{2}=2^{2}+x^{2}$$
Решаем полученное уравнение относительно $x$ :
$4 x^{2}-x^{2}=9 Rightarrow 3 x^{2}=9 Rightarrow x^{2}=3 Rightarrow H C=x=sqrt{3}$ (м)
Отсюда получаем, что
$A C=2 x=2 sqrt{3}$ (м)
А тогда искомая площадь
$mathrm{S}_{Delta A B C}=frac{(2 sqrt{3})^{2} cdot sqrt{3}}{4}=frac{12 sqrt{3}}{4}=3 sqrt{3}$ (м2)
Ответ. $mathrm{S}_{Delta A B C}=3 sqrt{3}$ (м2)
Остались вопросы?
Здесь вы найдете ответы.
Как можно вычислить площадь равсностороннего треугольника?
Согласно формуле, по которой вычисляется площадь S треугольника с равными
сторонами, она равна:
S = √3/4*а, в которой а – это длина стороны фигуры.
Площадь можно также найти следующим образом:
S = a*h/2, где h – это высота.
Высоту можно вычислить, используя теорему Пифагора:
h = а² — (а/2)².
Как можно рассчитать площадь равностороннего треугольника, если известно,
что площадь треугольной фигуры, отсекаемой от него средней линией,
составляет 6 см. кв.?
Обозначим имеющийся треугольник с равными сторонами как АВС. Обозначим
длину стороны как а, и получим, что АВ=ВС=АС=а. Среднюю линию обозначим
как МК. Тогда Sмвк = 6 см. кв.
В случае с равносторонним треугольником:
S = а²√3/4
Зная свойство средней линии треугольника, можно записать следующее
равенство:
МК = АС/2 = а/2.
В этом случае площадь отсекаемого треугольника равна:
Sмвк = (а/2)²*√3/4 = а²√3/16 см.кв.
В условии дано, что Sмвк = 6 см.кв., тогда:
а²√3/16 = 6
а² = 96/√3.
Площадь равностороннего треугольника:
S = а²√3/4 = (96√3)/(4√3) = 96/4 =24 см.кв.
Как можно вычислить площадь равностороннего треугольника при условии, что
его периметр составляет 24 см.?
Найдем сторону равносторонней треугольной фигуры, разделив его периметр на
3:
а = 24:3 = 8 см.
Тогда площадь этой фигуры равна:
S =1/2a²sin 60° = 1/2*64*√3/2 = 16√3 см.кв.
Что представляет собой формула площади равностороннего треугольника?
Обозначив одну из сторон равносторонней треугольной фигуры как а, а
высоту, проведенную к ней, — как h, то формула расчета площади этой фигуры
будет выглядеть так:
S=ah/2.
Принимая во внимание то, что все стороны данной треугольной фигуры равны,
то его высоту можно выразить через сторону и вычислить, используя теорему
Пифагора:
h² = а²-(а/2)² = h² = а²- а²/4 = 3а²/4
h = (а√3)/2
Тогда площадь данной фигуры равна:
S = ½ a* h = ½ a*(а√3)/2 = (a²√3)/4
Как выразить длину стороны а из формулы площади равностороннего
треугольника?
Для расчета площади треугольника, длины всех сторон которого равны,
используется формула:
S=a²√3/4
Перенесем 4 в правую часть равенства:
4S=a²√3.
Тогда:
a² = 4S/√3
а = √4S/√3.
Какая формула используется для вычисления площади равностороннего
треугольника с длиной стороны а?
Если известно, что сторона равносторонней треугольной фигуры равна а, то
его площадь рассчитывается так:
S = а²√3/4.
Каким образом можно привести доказательство теоремы о площади
равностороннего треугольника?
Треугольник имеет два катета – АВ и ВС. Его гипотенуза – ВС. Так как
фигура является равносторонней, то АВ = АС.
Требуется доказать, что площадь треугольной фигуры, стороны которой
одинаковы, равна произведению длин его катетов, разделенному на два.
Превратим имеющийся треугольник в квадрат, проведя перпендикуляр из его
углов, и получим что:
ΔВАС = ΔВСD.
Площадь квадрата равна:
S = а*b.
Диагональ квадрата ВС является гипотенузой треугольника, которая делит
квадрат на 2 равные части. Из этого следует, что площадь треугольника
равна половине площади квадрата. Что и требовалось доказать.
Как вычислить площадь равностороннего треугольника со стороной длиной 9 см.?
Имеется треугольник АВС с равным сторонами.
ВН = 9 см.
Площадь данной фигуры находится по формуле:
S=1/2*АС*ВН,
в которой АС – основание треугольной фигуре, по длине равное любой из
сторон (равносторонний Δ), ВН – высота.
Предположим, что АС = 2а см. Тогда:
АН = АС/2 = ½*2а = а см.
Согласно теореме Пифагора:
АВ² = ВН²+АН².
В данном случае:
(2а)² = 9²+а²
Переносим а² в правую часть уравнения:
4а²-а² = 81
Упрощаем:
3а² = 81.
Отсюда:
а² = 81/3 = 27
а=√27=√9×3=3√3 см.
Теперь можно найти площадь:
S=1/2*9*3√3=1/2*27/√3=27√3/2=13,5√3 см.кв.
Какому числу равна площадь равностороннего треугольника с основанием длиной
6 см.?
Известна формула расчета площади треугольника:
S=1/2*h*b.
Проведем высоту h, которая в равностороннем треугольнике представляет
собой также биссектрису и медиану.
Воспользуемся теоремой Пифагора для вычисления высоты:
h = √(36-9) = √27 см.
Тогда:
S = h*3 = 3√27 см.кв.
Возможно ли привести доказательство того, что площадь равностороннего
треугольника равна √3*a²/4, в которой длина его стороны обозначена как а?
Доказать, что приведенное в задании утверждение является верным, можно,
если превратить имеющуюся треугольную фигуру в параллелограмм/, площадь
которого равна произведению длины стороны и высоты.
Параллелограмм состоит из двух треугольников, которые равны. Это значит,
что площадь одной из треугольных фигур находится так:
S = a*h /2.
Высоту можно выразить через определение синуса.
Все углы в равносторонней треугольной фигуре равны и составляют 60
градусов (180/3).
sin(60) = V3/2.
Из определения синуса следует:
h/a = sin(60).
Это значит, что:
h = a*V3/2.
Значит:
S = a*a*V3/4.
Почему площадь равностороннего треугольника равна a^2√3/4?
Известно, что площадь любого треугольника можно найти по формуле:
S = 1/2*a*b*sinA,
в которой стороны треугольника обозначены как а и b, а угол, образованный
ими, — как А.
Доказано, что каждый угол равносторонней треугольной фигуры составляют 60
градусов (sin60 =sqrt(3)/2), а его стороны имеют одинаковые длины. Если
подставить эти значения в формулу, то получим:
S = a22√3/4.
Как найти площадь равностороннего треугольника при условии, что длина каждой
его стороны составляет 12 см.?
Площадь треугольника с равными сторонами вычисляется по формуле:
S = √3/4*a².
В данном случае:
S= √3/4*12²= √3*144 /4*1 = 36√3 ≈ 62,35 см.кв.
Согласно формуле Герона:
S = √(р(р-а)(р-a)(p-a))
Для данного треугольника:
Р = 12*3 = 36 см.
Р = р/2 = 36/2 = 18 см.
Тогда:
S = √ (18× (18-12)³) = √(18*6³) = √(18×216)=√3888 ≈ 62,35 см. кв.
Как вычислить площадь правильного равностороннего треугольника, зная радиус
круга R?
Площадь треугольника с одинаковыми сторонами считается как:
S = a²√3/4.
Радиус r окружности, которая вписана в данный Δ, равен a√3/6. Значит:
а = 2√3r.
Считаем площадь треугольника:
S = 4*3r²√3/4 = 3√3r².
Радиус R окружности, которая описана около правильной треугольной фигуры,
равен a/√3. Следовательно, а = R√3.
В этом случае:
S = R²*3√3/4 = 3√3R²/4.
Известно, что площадь правильного треугольника равна 100√3 м.кв. Как
вычислить его сторону?
Площадь треугольника равна:
(a²√3)/4.
В данном случае:
100√3=(a²√3)/4
Тогда:
a²√3=400√3.
Находим а:
a²√3 = 400√3
a² = 400
a = 20 см.
Чему равна площадь правильного треугольника при условии, что диаметр
окружности, вписанной в него, = 10 см.?
Если d = 10 см., то r = 10/2 = 5 см.
Известно, что:
r = а√3/6, где а – это длина стороны правильного Δ.
Значит:
5 = а√3/6.
Отсюда:
а = 30/√3 = 10√3 см.
Тогда:
SΔ = a²√3/4 =(10√3)³ *√3/4 = 75√3 см. кв.
Чему равна площадь правильного треугольника со стороной 4 дм.?
Известно, что:
S = 1/2 * a * a sin 60 = 1/2 * 4 * 4 * √3/2 = 4√3 дм.кв.
Площадь также можно найти так:
S = a²√3/4 = 16√3/4 = 4√3 дм.кв.
Как найти площадь правильного треугольника, зная, что длина описанной около
него окружности равна 4Пи см.?
Длина окружности через радиус находится так:
L=2πR.
Значит:
R=L/2π=4π/2π=2 у.е.
Имеем правильный треугольник, значит длина его стороны:
a=R*√3=2√3 у.е.
Можем найти SΔ:
S = √3/4a² = √3/43*3 = 3√3 у.е.кв.
Чему равна площадь правильного треугольника и его стороны, если его высота =
14 см.?
В правильном треугольнике длины всех сторон одинаковы. Это значит, что
каждую из них можно обозначить как х. Тогда:
Р (периметр) = х + х + х = 3х см.
Площадь будет равна:
S = 1/2 h * x = 14/2*x = 7х см.кв.
Как найти площадь правильного треугольника с равными сторонами при условии,
что радиус круга R?
Площадь треугольной фигуры с равными сторонами считается как:
S = a²√3/4.
Радиус окружности, вписанной в этот Δ, составляет a√3/6. Тогда а = 2√3r.
Находим площадь треугольника:
S = 4*3r²√3/4 = 3√3r².
Радиус R окружности, которая описана около правильного Δ, составляет a/√3.
Это означает, что а = R√3.
Теперь можем высчитать площадь треугольника:
S = R²*3√3/4 = 3√3R²/4.
Как найти площадь правильного треугольника при условии, что расстояние от
его центра до вершины составляет 2 м.?
Центр правильно треугольной фигуры также является центральной точкой
описанной около нее окружности. Ее радиус представляет собой расстояние от
центра до вершины фигуры:
а=R√3=2√3
Все углы в правильном треугольнике являются одинаковыми и равны по 60
градусов (180/3).
Площадь треугольной фигуры рассчитывается как:
а²sin60°/2=(2√3)²√3/2/2=6√3 м.кв.
Как найти площадь правильного треугольника, если определено, что сторона
имеет длину, аналогичную длине стороны ромба с диагоналями 10 см. и 12 см.?
Предположим, что BD = 10 см., а АС = 12 см.
Диагонали ромба перпендикулярны и делятся на две равные части, пересекаясь
в определенной точке.
ΔАВО: ∠АОВ = 90°, АО = АС/2 = 6, ВО = BD/2 = 5.
Согласно теореме Пифагора:
АВ = √(АО² + ВО²) = √(36 + 25) = √41.
Треугольник имеет равные стороны, длина каждой из которых аналогична длине
стороны ромба:
а = √41.
Тогда:
SΔ = a²√3/4 = 41√3/4 см.кв.
Как найти площадь правильного треугольника периметром 6 см.?
Если длина стороны правильного треугольника указана, то его площадь
вычисляется следующим образом:
S = a²√3/4.
Согласно определению правильного треугольника, длины всех его сторон
одинаковые. Исходя из этого можно найти его сторону, разделив периметр на
три:
а = 6/3 = 2 см.
Ищем площадь, подставив в равенство значение а:
S = 2²√3/4 = S 4√3/4 = √3 см.кв.
Как найти площадь правильного треугольника при условии, что окружность,
которая вписана в него, имеет радиус длиной 4 см.?
Площадь треугольника, имеющего стороны одинаковой длины, может быть
рассчитана через длину его стороны без применения формулы радиуса
окружности, которая вписана в него. Для данной фигуры верно утверждение о
том, что высота, биссектриса и медиана делятся в точке пересечения в
отношении 2:1. При схематичном изображении можно увидеть, что треугольная
фигура АВС включает 6 треугольников с прямыми углами, которые имеют
одинаковый катет (R) и гипотенузу (АО=ВО=СО). Следовательно, площадь
треугольника АВС будет представлять собой сумму площадей всех 6
треугольников, формирующих его.
Какова формула вычисления площади равностороннего треугольника со стороной
а?
Если сказано, что сторона равносторонней треугольной фигуры равна а, то
его площадь можно найти:
S = a²√3/4.
Как определить, чему равна длина стороны треугольника с равными сторонами,
зная формулу, по которой вычисляется площадь равностороннего треугольника
(S=√3/4 а²) и то, что она равна 9√3см²?
Если S=√3/4 а², то в данном случае S=9√3, что означает: 9√3=√3/4 а².
Выразим а²:
а² = 9√3:√3/4 = 9√3 x 4√3 = 36
а = +-√36 = +- 6.
Так как длина стороны не может быть отрицательным числом, то a = 6 см.
Какой вид имеет формула, которая отражает зависимость площади
равностороннего треугольника от длины его сторон?
Доказано, что равносторонний треугольник имеет равные углы по 60 градусов.
Также известна формула вычисления площади данной фигуры путем умножения
длин двух его сторон и синуса угла, который они образуют:
S = 1/2*a*a*sin 60 = a²√3/4 см.кв.
Чему равна площадь равностороннего треугольника и длина его медианы, если
известно, что его сторона составляет а?
Если указано, что длина стороны равностороннего треугольника составляет а,
то его площадь равна:
S=a²√3/4.
Медиана, проведенная в треугольнике с равными сторонами, также
представляет собой его биссектрису и высоту. Из этого следует, что:
h=a√3/2.
Ответ: Площадь треугольника = a²√3/4 см.кв., его медиана = a√3/2 см.
Как определить площадь равностороннего треугольника со стороной, длина
которой составляет 8√2 см?
В случае с треугольником с равными сторонами, высота представляет собой
также медиану, делящую на две равные части сторону, на которую она
опущена. Если применить в данном случае теорему Пифагора, то высота равна:
h = √((8√2)²-(4√2)²)=4√6 см.
Теперь есть возможность найти площадь:
S = (1/2)*8√2*4√6 = 32√3 см. кв.
Площадь также можно найти по формуле для треугольника с равными сторонами:
S =(√3/4)*a² или S =(√3/4)*128 = 32√3 см. кв.
Дано два равносторонних треугольника, площадь одного из которых превышает
площадь другого в три раза. Чему будет равна сторона второго равностороннего
треугольника, при условии, что сторона первого из них составляет 1 см.?
Для расчета площади треугольника с равными сторонами есть формула:
S = a²√3/4.
Найдем площадь меньшего из треугольников, подставив значение а:
S₁ = 12 √3/4 = √3/4 см.кв.
Известно, что площадь второго треугольника больше площади первой фигуры в
три раза. Тогда:
S₂ = 3√3/4.
Очевидно, что сторона большего треугольника составляет √3 см.
Сторона равностороннего треугольника равна 14 см. Чему будет равна его
площадь, умноженная на √3?
Формула площади для треугольника с равными сторонами:
S = а²*√3/4.
Подставляем значение а:
S = 14²*√3/4 = 49√3 см. кв.
Умножаем полученное число на √3:
49√3*√3 = 49*3 = 147 см.
Читать дальше: как найти площадь круга.